How to find the amplitude value of AC voltage?
In our household electrical network, the current, effective, alternating current voltage Ud is equal to 220 volts. The maximum amplitude value of the voltage in the network is: Um = Ua = Ud x 1.41 = 220 x 1.41 = 310.2 volts.
Interesting materials:
How to properly turn off PSP? How to take disciplinary action correctly? How is advance payment and salary paid correctly? How to grow ginger correctly? How to properly grow a ficus from a shoot? How to properly grow a chestnut from a nut? How to properly take a shoot from a ficus? How to properly fix polycarbonate to a greenhouse? How to close a company correctly? How to close roses correctly?
Features of alternating voltage, current
Generators that produce electricity are designed so that the voltage, the rate of change of charge in our power lines, changes according to a harmonious law:
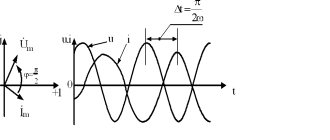
u = Umsin(ωt+φ0), i = Imsin(ωt+φ0).
Designations:
- u, i – instantaneous values (at an arbitrary moment in time);
- Um, Im – amplitude values (maximum);
- Um – voltage amplitude;
- Im – current amplitude;
- t – time;
- value ω – cyclic frequency.
The value ω is related to the linear frequency ν by the expression:
ω = 2πν:
- π = 3.14 – mathematical constant;
- ν = 50 Hz (for electrical networks in our country).
The product ωt is called the phase:
ωt = φ.
Measured in radians (rad), φ0 is the initial phase, often equal to zero. Using the cos function in formulas does not change the meaning of physical expressions.
If a voltage varying according to a harmonious law is applied to an ordinary resistor (it can be an incandescent lamp, a thermal heater), then particles will begin to move through it, the nature of their movement changing according to the same law.
The change in values will be synchronous, the phases will be the same. This resistance is called active.
Effective values
The arithmetic mean value of voltage and the rate of charge change over a period is zero, so it cannot be used to characterize the oscillatory process. The squares of these quantities, their average values are always positive.
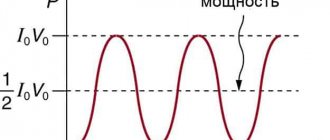
The square of the average current value is equal to half the square of the amplitude value:
Is2 = Im2/2.
Is – average value. It is also called effective (another name is acting):
Is = Im/√2.
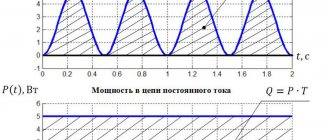
The square of the current is proportional to the amount of energy generated in the conductor: Q ~ Is2.
The effective value of the alternating current is equal to the direct current, at which the same amount of heat is generated during the time t = T. For the effective voltage value the formula is similar:
Us = Um/√2.
It is the effective values that are shown by measuring instruments.
Effective and average values of periodic EMF and currents
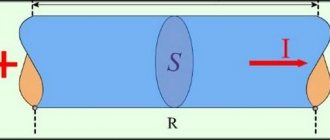
The concept of the mean square (rms) value can be obtained by considering the thermal effect of current. Let the resistance of the circuit in which periodic current flows be equal to R.
Then, according to the Joule–Lenz law, the amount of heat released in this resistance over an elementary period of time
dt
will be equal to , and over one full period – .
Let us denote by I
such a direct current that, over a period of time
T,
the in resistance R.
Then we have:
, where .
Value I
, determined by the last equality, is called
the effective or root-mean-square value of the periodic current.
For a sinusoidal current we have: and, therefore,
.
The effective value of the periodic sinusoidal EMF is determined similarly:
.
Instruments used to measure periodic EMF (currents) show their effective values.
In addition to the effective values of periodic EMF (currents), their average values are used.
The average value of a harmonically varying current (EMF) is understood as the value corresponding to the positive half-wave:
.
Likewise.
For harmonic functions:
amplitude coefficient is the ratio of the amplitude value of the current (EMF) to the effective value: ;
The form factor is the ratio of the effective current value (EMF) to the average value: .
Phase difference between voltage and current . AC circuit parameters .
Under the phase difference ( φ
) voltage and current understand the difference in the initial phases of voltage () and current (): .
Active resistance in the AC circuit.
Inductive reactance in an AC circuit.
Capacitance in an AC circuit.
The concept of the mean square (rms) value can be obtained by considering the thermal effect of current. Let the resistance of the circuit in which periodic current flows be equal to R.
Then, according to the Joule–Lenz law, the amount of heat released in this resistance over an elementary period of time
dt
will be equal to , and over one full period – .
Let us denote by I
such a direct current that, over a period of time
T,
the in resistance R.
Then we have:
, where .
Value I
, determined by the last equality, is called
the effective or root-mean-square value of the periodic current.
For a sinusoidal current we have: and, therefore,
.
The effective value of the periodic sinusoidal EMF is determined similarly:
.
Instruments used to measure periodic EMF (currents) show their effective values.
In addition to the effective values of periodic EMF (currents), their average values are used.
The average value of a harmonically varying current (EMF) is understood as the value corresponding to the positive half-wave:
.
Likewise.
For harmonic functions:
amplitude coefficient is the ratio of the amplitude value of the current (EMF) to the effective value: ;
The form factor is the ratio of the effective current value (EMF) to the average value: .
Phase difference between voltage and current . AC circuit parameters .
Under the phase difference ( φ
) voltage and current understand the difference in the initial phases of voltage () and current (): .
Active resistance in the AC circuit.
Inductive reactance in an AC circuit.
Capacitance in an AC circuit.
Definition and formula of EMF
Definition
A scalar physical quantity that is equal to the work of external forces to move a unit positive charge is called electromotive force (EMF)
, acting in a circuit or section of a circuit.
EMF is denoted by $\varepsilon$ . Mathematically, we write the definition of EMF as: $$\varepsilon=\frac{A}{q}(1)$$
where A is the work of external forces, q is the charge on which the work is performed.
The electromotive force of the source is numerically equal to the potential difference at the ends of the element if it is open, which makes it possible to measure the EMF by voltage.
The EMF that acts in a closed circuit can be defined as the circulation of the tension vector of external forces:
$$\varepsilon=\oint_{L} \bar{E}^{*} d \bar{l}(2)$$
where $\bar{E}^{*}$ is the field strength of external forces. If the field strength of external forces is not zero only in part of the circuit, for example, on segment 1-2, then integration in expression (2) can be carried out only over this section. Accordingly, the EMF acting on circuit section 1-2 is defined as:
$$\varepsilon=\int_{1}^{2} \bar{E}^{*} d \bar{l}(3)$$
Formula (2) gives the most general definition of EMF, which can be used for any cases.
Ohm's law for an arbitrary section of a circuit
The section of the chain on which external forces act is called heterogeneous. It satisfies the following equality:
$$U_{12}=\varphi_{1}-\varphi_{2}+\varepsilon_{12}(4)$$
where U12=IR21 – voltage drop (or voltage) in circuit section 1-2 (I-current); $\varphi_{1}-\varphi_{2}$ – potential difference between the ends of the section; $\varepsilon_12$ is the electromotive force contained in the circuit section. $\varepsilon_12$ is equal to the algebraic sum of the emf of all sources that are located in a given area.
It should be taken into account that EMF can be positive and negative. The EMF is called positive if it increases the potential in the direction of the current (the current flows from the minus to the plus of the source).
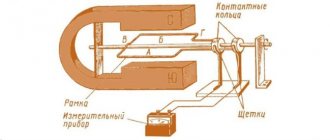
Definition of electromagnetic induction
The occurrence of an electric current in a conductor moving in a magnetic field is called the phenomenon of induction in moving conductors. When a conductor moves in a magnetic field, its free electrons move relative to the conductor under the influence of the Lorentz force. The phenomenon of electromagnetic induction was discovered by Faraday in 1831 in a conducting circuit. He noticed that in a closed conducting circuit, when the flux of magnetic induction changes through the surface that the circuit limits, an electric current appears. This is also the phenomenon of electromagnetic induction, the resulting current in the circuit is called induction .
So, the phenomenon of electromagnetic induction consists in the occurrence of an electric current in a closed conductor when the flux of magnetic induction covered by the circuit changes. In this case, the circuit can be stationary.
Are you an expert in this subject area? We invite you to become the author of the Directory Working Conditions