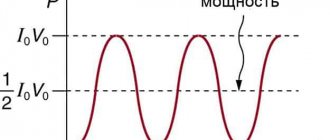
Что такое мгновенное амплитудное и действующее значение переменного тока?

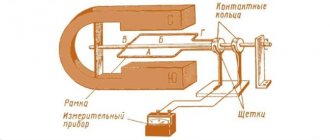
Как найти амплитудное значение напряжения переменного тока?

В нашей бытовой электросети действующее, эффективное, напряжение переменного тока Uд равно 220 вольт . Максимальное, амплитудное значение напряжения в сети равно: Um = Ua = Uд х 1,41 = 220 х 1,41 = 310,2 вольт.

Интересные материалы:

Как правильно выключить PSP? Как правильно вынести дисциплинарное взыскание? Как правильно выплачивается аванс и зарплата? Как правильно выращивать имбирь? Как правильно вырастить фикус из отростка? Как правильно вырастить каштан из ореха? Как правильно взять отросток у фикуса? Как правильно закрепить поликарбонат на теплице? Как правильно закрыть фирму? Как правильно закрыть розы?

Особенности переменного напряжения, тока

Генераторы, вырабатывающие электроэнергию, сконструированы так, что напряжение, скорость изменения заряда в наших линиях электропередач меняются по гармоничному закону:

u = Umsin(ωt+φ0), i = Imsin(ωt+φ0).

Обозначения:

u, i – мгновенные значения (в произвольный момент времени);
Um, Im – амплитудные значения (максимальные);
Um – амплитуда напряжения;
Im – амплитуда тока;
t – время;
величина ω – циклическая частота.

Величина ω связана с линейной частотой ν выражением:

ω = 2πν:

π = 3,14 – математическая константа;
ν = 50 Гц (для электрических сетей в нашей стране).

Произведение ωt называют фазой:

ωt = φ.

Измеряют в радианах (рад), φ0 – начальная фаза, зачастую равна нулю. Использование в формулах функции cos не изменяет смысла физических выражений.

Если напряжение, изменяющееся по гармоничному закону, приложить к обычному резистору (в его роли может быть лампа накаливания, тепловой нагреватель), то через него начнут двигаться частицы, характер движения которых изменяется по такому же закону.

Изменение величин будет синхронным, фазы – одинаковыми. Такое сопротивление называют активным.

Эффективные значения

Среднее арифметическое значение напряжения, скорости изменения заряда за период равно нулю, поэтому его нельзя использовать для характеристики колебательного процесса. Квадраты этих величин, их средние значения всегда положительны.

Квадрат среднего значения силы тока равен половине квадрата амплитудного значения:

Is2 = Im2/2.

Is – среднее значение. Его называют еще эффективным (другое название – действующим):

Is = Im/√2.

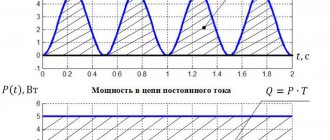
Квадрат силы тока пропорционален количеству энергии, образующейся в проводнике: Q ~ Is2.

Эффективное значение величины переменного тока равно величине постоянного, при котором за время t = T образуется такое же количество теплоты. Для действующего значения напряжения формула аналогична:

Us = Um/√2.

Именно эффективные значения показывают измерительные приборы.

Действующие и средние значения периодических ЭДС и токов

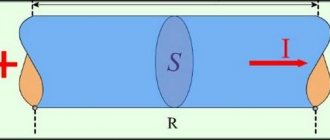
Понятие о среднем квадратичном (действующем) значении можно получить, рассматривая тепловое действие тока. Пусть сопротивление цепи, в которой протекает периодический ток, равно R.

Тогда согласно закону Джоуля – Ленца количество теплоты, выделяемой в этом сопротивлении за элементарный промежуток времени
dt
, будет равно , а за один полный период – .

Обозначим через I

такой постоянный ток, который за промежуток времени
Т
выделит в сопротивлении
R
такое же количество тепла. Тогда имеем:

, откуда .

Величина I

, определяемая последним равенством, называется
действующимили средним квадратичнымзначением периодического тока.
Для синусоидального тока имеем: и, следовательно,

Аналогично определяется действующее значение периодической синусоидальной ЭДС:

Приборы, применяемые для измерения периодических ЭДС (токов), показывают их действующие значения.

Кроме действующих значений периодических ЭДС (токов), используют их средние значения.

Под среднимзначением гармонически изменяющегося тока (ЭДС) понимают значение соответствующее положительной полуволне:

Аналогично .

Для гармонических функций:

коэффициент амплитуды — это отношение амплитудного значения тока (ЭДС) к действующему значению: ;

коэффициент формы — это отношение действующего значения тока (ЭДС) к среднему значению: .

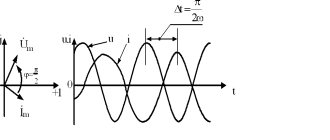
Разность фаз напряжения и тока. Параметры цепей переменного тока.

Под разностью фаз (φ

) напряжения и тока понимают разность начальных фаз напряжения () и тока (): .

Активное сопротивление в цепи переменного тока.

Индуктивное сопротивление в цепи переменного тока.

Емкостное сопротивление в цепи переменного тока.

Обозначим через I

, откуда .

Величина I

Аналогично определяется действующее значение периодической синусоидальной ЭДС:

Приборы, применяемые для измерения периодических ЭДС (токов), показывают их действующие значения.

Кроме действующих значений периодических ЭДС (токов), используют их средние значения.

Аналогично .

Для гармонических функций:

коэффициент амплитуды — это отношение амплитудного значения тока (ЭДС) к действующему значению: ;

коэффициент формы — это отношение действующего значения тока (ЭДС) к среднему значению: .

Разность фаз напряжения и тока. Параметры цепей переменного тока.

Под разностью фаз (φ

) напряжения и тока понимают разность начальных фаз напряжения () и тока (): .

Активное сопротивление в цепи переменного тока.

Индуктивное сопротивление в цепи переменного тока.

Емкостное сопротивление в цепи переменного тока.

Определение и формула ЭДС

Определение

Скалярная физическая величина, которая равна работе сторонних сил по перемещению единичного положительного заряда, называется электродвижущей силой (ЭДС)

, действующей в цепи или на участке цепи. ЭДС обозначается $\varepsilon$ . Математически определение ЭДС запишем как:
$$\varepsilon=\frac{A}{q}(1)$$
где A – работа сторонних сил, q – заряд, над которым производится работа.

Электродвижущая сила источника численно равна разности потенциалов на концах элемента, если он разомкнут, что дает возможность измерить ЭДС по напряжению.

ЭДС, которая действует в замкнутой цепи, может бытьопределена как циркуляция вектора напряжённости сторонних сил:

$$\varepsilon=\oint_{L} \bar{E}^{*} d \bar{l}(2)$$

где $\bar{E}^{*}$ — напряженность поля сторонних сил. Если напряженность поля сторонних сил не равна нулю только в части цепи, например, на отрезке 1-2, тогда интегрирование в выражении (2) можно вести только по данному участку. Соответственно, ЭДС, действующая на участке цепи 1-2 определяется как:

$$\varepsilon=\int_{1}^{2} \bar{E}^{*} d \bar{l}(3)$$

Формула (2) дает самое общее определение ЭДС, которое можно использовать для любых случаев.

Закон Ома для произвольного участка цепи

Участок цепи, на котором действуют сторонние силы, называют неоднородным. Для него выполняется равенство:

$$U_{12}=\varphi_{1}-\varphi_{2}+\varepsilon_{12}(4)$$

где U12=IR21 – падение напряжения (или напряжение) на участке цепи 1-2 (I-сила тока); $\varphi_{1}-\varphi_{2}$ – разность потенциалов концов участка; $\varepsilon_12$ – электродвижущая сила, которую содержит участок цепи. $\varepsilon_12$ равна алгебраической сумме ЭДС всех источников, которые находятся на данном участке.

Следует учитывать, что ЭДС может быть положительной и отрицательной. ЭДС называют положительной, если она увеличивает потенциал в направлении тока (ток течет от минуса к плюсу источника).

Определение электромагнитной индукции

Возникновение электрического тока в проводнике, движущемся в магнитном поле, называют явлением индукцией в движущихся проводниках. В случае движения проводника в магнитном поле, его свободные электроны приходят в движение относительно проводника под воздействием силы Лоренца. Явление электромагнитной индукции обнаружил Фарадей в 1831 г. в проводящем контуре. Он заметил, что в замкнутом проводящем контуре при изменении потока магнитной индукции через поверхность, которую ограничивает контур, появляется электрический ток. Это также явление электромагнитной индукции, возникающий ток в контуре, называют индукционным.
Итак, явление электромагнитной индукции состоит в возникновении электрического тока в замкнутом проводнике при изменении потока магнитной индукции, охватываемого контуром. При этом контур может быть неподвижным.

Ты эксперт в этой предметной области? Предлагаем стать автором Справочника Условия работы