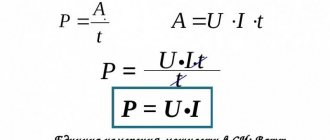Мощность в цепи переменного тока
Внутри схемы переменного электротока различается три вида мощностей: активного типа или Р, реактивного типа или Q, и полного типа или S. В первом случае стандартной единицей замеров является Ватт (Вт или W), при этом формула для вычисления активных мощностных параметров:
P = U × I × cos φ.
От характеристик коэффициента угла фазового сдвига или последнего показателя напрямую зависят расчеты положительной или отрицательной активной мощности.
Для замеров мощности реактивного типа применяется специальный вольт-ампер с обозначением «Вар» или Var.
Данной величиной характеризуются нагрузки, которые формируются внутри конструкций электротехнического типа под воздействием колебаний электромагнитных полей в цепях переменного синусоидального тока.
Расчет осуществляется на базе среднеквадратичных показателей напряжения и токовых параметров, умноженных на угловую синусоиду фазного сдвига, согласно значениям:
Q = U × I × sin φ.
В условиях значений на уровне 0/+90° синусовая величина будет положительной, а для показателей в пределах 0/-90° — только отрицательной. Замеры полной электромощности осуществляются исключительно в вольт-амперах (В·А или V·A).
Зависимость мощности от времени для переменного и постоянного тока
Величину, соответствующую произведению стандартного напряжения в зажимной области с показателями электротока периодического типа внутри цепи, целесообразно рассчитывать в соответствии с формулами:
S = U × I или S = √Р2 + Q2, где
- значение Р представлено активной мощностью;
- значение Q2 — показатель реактивной мощности.
Немаловажное значение отводится комплексной мощности, соответствующей импедансу. В любом случае необходимо учитывать, что положительная мощность соответствует P > 0, а отрицательные показатели — P < 0.
Крупными отечественными производителями электрической энергии генерируется переменный ток с так называемой промышленной частотой, равной 50 Гц, и показателями напряжения в пределах 10-20 кВ, а электрическое напряжение повышается на специальных трансформаторных подстанциях.
Расчеты и уравнения
Формула для комплексной мощности (единицы: ВА) в фазор форма:
S = V я ∗ = | S | ∠ φ { Displaystyle S = VI ^ {*} = | S | angle varphi} ,
куда V
обозначает напряжение в векторной форме, с амплитудой как среднеквадратичное значение, и
я
обозначает ток в векторной форме со среднеквадратичной амплитудой. Также по соглашению комплексно сопряженный из
я
используется, что обозначается я ∗ { displaystyle I ^ {*}} (или же я ¯ { displaystyle { overline {I}}} ), скорее, чем
я
сам. Это сделано потому, что в противном случае использование продукта VI для определения S приведет к количеству, которое зависит от исходного угла, выбранного для V или I, но определение S как VI * приводит к количеству, которое не зависит от исходного угла и позволяет связать S с P и Q.[5]
Другие формы комплексной мощности (единицы в вольт-амперах, ВА) получены из Z
, Загрузка сопротивление (единицы в Ом, Ом).
S = | я | 2 Z = | V | 2 Z ∗ { Displaystyle S = | I | ^ {2} Z = { frac {| V | ^ {2}} {Z ^ {*}}}} .
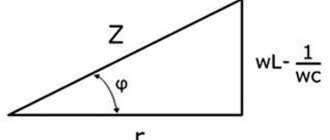
Следовательно, со ссылкой на треугольник мощности, реальная мощность (единицы измерения в ваттах, Вт) определяется как:
п = | S | потому что φ = | я | 2 р = | V | 2 | Z | 2 × р { displaystyle P = | S | cos { varphi} = | I | ^ {2} R = { frac {| V | ^ {2}} {| Z | ^ {2}}} times {R }} .
Для чисто резистивной нагрузки реальную мощность можно упростить до:
п = | V | 2 р { Displaystyle P = { frac {| V | ^ {2}} {R}}} .
р
обозначает сопротивление (единицы в Ом, Ом) нагрузки.
Реактивная мощность (единицы в вольт-амперах, реактивная мощность) рассчитывается как:
Q = | S | грех φ = | я | 2 Икс = | V | 2 | Z | 2 × Икс { Displaystyle Q = | S | грех { varphi} = | I | ^ {2} X = { frac {| V | ^ {2}} {| Z | ^ {2}}} times {X }} .
Для чисто реактивной нагрузки реактивная мощность может быть упрощена до:
Q = | V | 2 Икс { displaystyle Q = { frac {| V | ^ {2}} {X}}} ,
куда Икс
обозначает реактивное сопротивление (единицы в Ом, Ом) нагрузки.
Комбинирование, комплексная мощность (единицы в вольт-амперах, ВА) вычисляется обратно как
S = п + j Q { Displaystyle S = P + jQ} ,
и полная мощность (единицы в вольт-амперах, ВА) как
| S | = п 2 + Q 2 { displaystyle | S | = { sqrt {P ^ {2} + Q ^ {2}}}} .
Они схематично упрощены треугольником мощности.
Формула мощности переменного тока
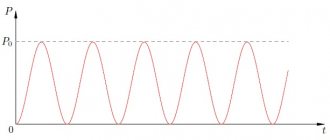
Мощностные показатели электротока переменного типа являются произведением токовых данных на напряжение, при этом уровень будет нулевым в условиях прохождения через нуль, но обязательно максимальным на пиковой амплитуде.
Несмотря на сложность измерения мощности, важно помнить, что такие данные не показательны, поэтому с практической точки зрения интерес представляет активная средняя мощность в определенном периоде.
Многочастотные системы
Поскольку среднеквадратичное значение можно рассчитать для любой формы сигнала, на его основе можно рассчитать полную мощность. Для активной мощности сначала может показаться, что необходимо рассчитать многие параметры продукта и усреднить их все. Однако более подробное рассмотрение одного из этих продуктовых терминов дает очень интересный результат.
А потому что ( ω 1 т + k 1 ) потому что ( ω 2 т + k 2 ) = А 2 потому что [ ( ω 1 т + k 1 ) + ( ω 2 т + k 2 ) ] + А 2 потому что [ ( ω 1 т + k 1 ) − ( ω 2 т + k 2 ) ] = А 2 потому что [ ( ω 1 + ω 2 ) т + k 1 + k 2 ] + А 2 потому что [ ( ω 1 − ω 2 ) т + k 1 − k 2 ] { displaystyle { begin {align} & A cos ( omega _ {1} t + k_ {1}) cos ( omega _ {2} t + k_ {2}) = {} & { гидроразрыв {A} {2}} cos left [ left ( omega _ {1} t + k_ {1} right) + left ( omega _ {2} t + k_ {2} right) right] + { frac {A} {2}} cos left [ left ( omega _ {1} t + k_ {1} right) — left ( omega _ {2} t + k_ {2} right) right] = {} & { frac {A} {2}} cos left [ left ( omega _ {1} + omega _ {2} right) t + k_ {1} + k_ {2} right] + { frac {A} {2}} cos left [ left ( omega _ {1} — omega _ {2} right) t + k_ {1} -k_ {2} right] end {выровнено}}}
Однако среднее по времени функции вида cos (ωt
+
k
) равен нулю при условии, что
ω
не равно нулю. Следовательно, единственные термины продукта, которые имеют ненулевое среднее значение, — это те, в которых частота напряжения и тока совпадает. Другими словами, можно рассчитать активную (среднюю) мощность, просто рассматривая каждую частоту отдельно и складывая ответы. Кроме того, если предполагается, что напряжение источника питания является одночастотным (что обычно так и есть), это показывает, что гармонические токи это плохо. Они увеличивают среднеквадратичный ток (поскольку будут добавлены ненулевые члены) и, следовательно, полную мощность, но они не будут влиять на передаваемую активную мощность. Следовательно, гармонические токи уменьшают коэффициент мощности. Гармонические токи можно уменьшить с помощью фильтра, установленного на входе устройства. Обычно это будет либо просто конденсатор (в зависимости от паразитного сопротивления и индуктивности в источнике питания), либо цепь конденсатор-индуктор. Активный коррекция коэффициента мощности Схема на входе, как правило, дополнительно снижает гармонические токи и поддерживает коэффициент мощности, близкий к единице.
В однофазной цепи
Для однофазной цепи используется формула определения полной мощности: S = U × I, где
- S — показатели полных мощностных характеристик (Ва);
- I — уровень действующей силы электротока с учетом обмотки генератора (А);
- U — параметры расчетного действующего значения напряжения в генераторе (В).
Полные мощностные характеристики, учитываемые при стандартных самостоятельных расчетах, влияют на габариты генератора с переменными показателями электрического тока, что обусловлено поперечным сечением и числом витков обмоточных проводов, а также толщиной изоляционного материала. Для активного и реактивного сопротивления важна мощность, расходуемая при активном сопротивлении, и в реактивной части.
Однофазные электрические цепи переменного тока
Реактивные мощностные показатели обуславливаются энергетическими колебаниями в условиях формирования и потери электрических или магнитных полей. Запасаемая внутри поля такого сопротивления электроэнергия поступательно возвращается обратно на генератор, который подключается к стандартной электрической цепи.
Наличие реактивных токов между реактивным приемником и генератором, которые имеют индуктивное и емкостное сопротивление, способствует бесполезной загрузке линии и генератора, что сопровождается дополнительными энергетическими потерями.
Фактор силы
Основная статья: Фактор силы
Отношение активной мощности к полной мощности в цепи называется фактор силы. Для двух систем, передающих одинаковое количество активной мощности, система с более низким коэффициентом мощности будет иметь более высокие циркулирующие токи из-за энергии, которая возвращается к источнику из накопителя энергии в нагрузке. Эти более высокие токи вызывают более высокие потери и снижают общую эффективность передачи. Схема с более низким коэффициентом мощности будет иметь более высокую полную мощность и более высокие потери при том же количестве активной мощности. Коэффициент мощности равен 1,0, когда напряжение и ток находятся в фаза. Он равен нулю, когда ток опережает или отстает от напряжения на 90 градусов. Когда напряжение и ток сдвинуты по фазе на 180 градусов, коэффициент мощности отрицательный, и нагрузка подает энергию в источник (примером может быть дом с солнечными батареями на крыше, которые подают энергию в электросеть, когда солнце светит). Коэффициенты мощности обычно указываются как «опережающие» или «запаздывающие», чтобы показать знак сдвига фаз тока по отношению к напряжению. Напряжение обозначается как база, с которой сравнивается угол тока, что означает, что ток рассматривается как «опережающее» или «запаздывающее» напряжение. Если форма волны чисто синусоидальная, коэффициент мощности — это косинус фазового угла ( φ { displaystyle varphi} ) между синусоидальными сигналами тока и напряжения. В технических паспортах оборудования и паспортных табличках коэффициент мощности часто сокращается как » потому что ϕ { displaystyle cos phi} » по этой причине.
Пример: активная мощность 700 Вт а фазовый угол между напряжением и током составляет 45,6 °. Коэффициент мощности равен cos (45,6 °) = 0,700. Тогда кажущаяся мощность равна: 700 Вт / cos (45,6 °) = 1000 ВА. Концепция рассеивания мощности в цепи переменного тока поясняется и проиллюстрирована на примере.
Например, коэффициент мощности 0,68 означает, что только 68 процентов от общего подаваемого тока (по величине) фактически выполняет работу; остальные 32% не работают. Обычно коммунальные предприятия не взимают с потребителей плату за потери реактивной мощности, поскольку они не выполняют реальной работы для потребителя. Однако, если на источнике нагрузки потребителя наблюдается неэффективность, из-за которой коэффициент мощности падает ниже определенного уровня, коммунальные предприятия могут взимать с потребителей плату, чтобы покрыть увеличение использования топлива электростанцией и снижение мощности линии и станции.
В трехфазной цепи
Мощностные показатели переменного тока при равномерной трехфазной нагрузке определяются наличием равноценного тока, протекающего по проводникам фазы. В этом случае показатели силы тока в условиях использования нулевого проводника составляют «О». Формула для расчета мощности переменного тока в условиях трехфазной сети: Р = 3 × U φ × I × соs(φ).
Симметричная (равномерная) нагрузка фаз в трехпроводной цепи трехфазного тока
Протекание внутри фазных проводников различных по величине токов представляет собой несимметричную, или неравномерную нагрузку. При этом именно несимметричная нагрузка сопровождается протеканием тока по нулевым или нейтральным проводам, поэтому уровень мощностных показателей определяется в соответствии со стандартной и общеизвестной формулой:
Робщая = Uа × Iа × соs(φ1) + Ub × Ib × соs(φ2) + Uс × Iс × соs(φ3).
Средняя мощность в активной нагрузке
Мощностные параметры электросети или любой установки являются наиболее важными данными практически любого электрического прибора. Передача проходящих или потребляемых мощностных характеристик активного типа осуществляются в течение определенного периода времени.
Табличные значения средних мощностных характеристик основных бытовых приборов
| Устройство | Показатели |
| Зарядное устройство | 2,0 Вт/час |
| Люминесцентные лампы «ДРЛ» | 50 Вт/час и более |
| Электрический чайник | 1,5 кВт/час |
| Акустические системы | 30 Вт/час |
| Стиральная машина | 2,5 кВт/час |
| Мойка под высоким давлением | 3,5 кВт/час |
| Инверторы полуавтоматического типа | 3,5 кВт/час |
| Кухонный блендер | 1,0-1,2 кВт/час |
| Микроволновая СВЧ-печь | 1,8 кВт/час |
| Кухонные тостеры | 1,2 кВт/час |
| Телевизор | 0,2 кВт |
| Холодильник | 0,4 кВт |
| Пылесос | 1,0 кВт |
| Компьютер стационарный | 0,55 кВт |
| Электрическая плита | 2,5 кВт/час |
| Фен для сушки волос | 1,0 кВт/час |
| Утюг | 1,0 кВт/час |
| Электрическая духовка | 1,2 кВт/час |
| Электрический обогреватель | 1,4 кВт/час |
Мощность при наличии сдвига фаз между током и напряжением
В условиях переменного электротока совпадения в токовом направлении и напряжении отмечаются только при отсутствии катушечной индукции и конденсаторов. В этом случае векторное направление тока и напряжения идентичны. Присутствие в схеме катушек и конденсатора сопровождается совпадением токовых фаз и показателей напряжения, но векторное вращение происходит на одинаковой скорости и при неизменных параметрах угла.
Фазовое смещение или сдвиг совпадает с углом, который наблюдается между векторными радиусами токовых показателей и параметров напряжения, а отставание в этих критериях провоцирует несовпадение.
Сдвиг фаз переменного тока и напряжения
При этом мощностные характеристики являются отрицательными за счет произведения положительной и отрицательной величин. В подобных условиях электрическая цепь внешнего типа становится стандартным источником электроэнергии. Незначительный объем энергии, поступающей в цепь на положительных показателях мощности, осуществляет возврат только при наличии отрицательных значений.
Продолжительность частей периода напрямую зависит от уровня фазового сдвига, при этом показатели смещения определяются длительностью отрицательных мощностей, или так называемыми средними мощностными характеристиками электрического тока.
Формулы действительных чисел
Идеальный резистор не накапливает энергии; поэтому ток и напряжение совпадают по фазе. Следовательно, нет реактивной мощности и п = S { Displaystyle P = S} (с использованием соглашение о пассивных знаках). Поэтому для идеального резистора
п = S = V р M S я р M S = я р M S 2 р = V р M S 2 р { displaystyle P = S = V _ { mathrm {RMS}} I _ { mathrm {RMS}} = I _ { mathrm {RMS}} ^ {2} R = { frac {V _ { mathrm {RMS}} ^ {2}} {R}} , !} .
Для идеального конденсатора или катушки индуктивности нет передачи полезной мощности; так что вся мощность реактивная. Следовательно, для идеального конденсатора или индуктора:
п = 0 Q = | S | = V р M S я р M S = я р M S 2 | Икс | = V р M S 2 | Икс | { displaystyle { begin {align} P & = 0 Q & = | S | = V _ { mathrm {RMS}} I _ { mathrm {RMS}} = I _ { mathrm {RMS}} ^ {2} | X | = { frac {V _ { mathrm {RMS}} ^ {2}} {| X |}} end {align}}} .
куда Икс { displaystyle X}
это реактивное сопротивление конденсатора или катушки индуктивности.
Если Икс { displaystyle X} определяется как положительный для катушки индуктивности и отрицательный для конденсатора, тогда модуль знаки можно удалить с S и X и получить
Q = я р M S 2 Икс = V р M S 2 Икс { displaystyle Q = I _ { mathrm {RMS}} ^ {2} X = { frac {V _ { mathrm {RMS}} ^ {2}} {X}}} .
Мгновенная мощность определяется как:
п inst ( т ) = V ( т ) ⋅ я ( т ) { Displaystyle Р _ { текст {inst}} (т) = В (т) CDOT I (т)} ,
куда V ( т ) { Displaystyle V (т)} и я ( т ) { Displaystyle I (т)} — изменяющиеся во времени формы сигналов напряжения и тока.
Это определение полезно, потому что оно применимо ко всем сигналам, независимо от того, являются они синусоидальными или нет. Это особенно полезно в силовой электронике, где распространены несинусоидальные сигналы.
В общем, инженеров интересует активная мощность, усредненная за период времени, будь то цикл низкочастотной линии или период переключения высокочастотного преобразователя мощности. Самый простой способ получить этот результат — взять интеграл мгновенного расчета за желаемый период:
п средний = 1 т 2 − т 1 ∫ т 1 т 2 V ( т ) я ( т ) d т { displaystyle P _ { text {avg}} = { frac {1} {t_ {2} -t_ {1}}} int _ {t_ {1}} ^ {t_ {2}} V (t) I (t) , operatorname {d} t} .
Этот метод расчета средней мощности дает активную мощность независимо от гармоническое содержание формы волны. В практических приложениях это будет выполняться в цифровой области, где расчет становится тривиальным по сравнению с использованием среднеквадратичных значений и фазы для определения активной мощности:
п средний = 1 п ∑ k = 1 п V [ k ] я [ k ] { displaystyle P _ { text {avg}} = { frac {1} {n}} sum _ {k = 1} ^ {n} V [k] I [k]} .
Баланс мощностей
Самостоятельное нахождение некоторых электротехнических неизвестных, как правило, требует обязательной проверки правильности полученных значений с учетом баланса мощностей.
В соответствии с общепринятыми характеристиками, баланс в электрической цепи базируется на законе сохранения энергии, поэтому суммарные потребляемые и отдаваемые мощности должны быть равными.
При расчетах учитываются показатели эквивалентного сопротивления и знакомый большинству из курса физики закон Ома.
Допускаются небольшие расхождения в значениях, что обуславливается стандартными округлениями, осуществляемыми в процессе выполнения самостоятельных расчетов. Таким образом, вне зависимости от уровня сложности создаваемой цепи баланс обязательно должен сходиться, что является гарантией сохранения работоспособности и полной безопасности эксплуатации.