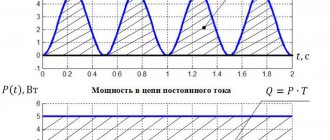
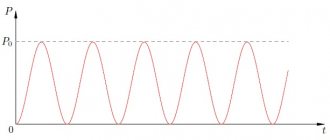
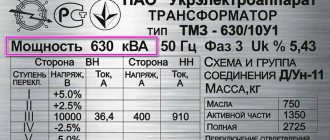
Закон Джоуля-Ленца
Замечание 1
Первым сформулировал зависимость выделения теплоты от силы электрического тока Джеймс Джоуль, что произошло в 1841 году. Позднее это сделал Эмиль Ленц. Так появляется закон Джоуля-Ленца, позволяющий рассчитывать мощность электронагревателей наряду с потерями на тепловыделение в линиях электропередач.
Ты эксперт в этой предметной области? Предлагаем стать автором Справочника Условия работы
В словесной формулировке, согласно исследованиям этих ученых, закон будет звучать таким образом: количество выделяемой в определенном объеме проводника теплоты в момент протекания электрического тока оказывается прямо пропорциональным произведению величины напряженности электрического поля и плотности электрического тока. Формула записывается так:
$w=\vec{j}\vec{E} = QE^2$, где:
- $w$ представляет мощность выделяемого тепла в единице объема;
- $\vec{j}$ считается плотностью электрического тока;
- $\vec{E}$ — напряженность электрического поля;
- $Q$ -проводимость среды.
Принимая во внимание неизменность со временем силы тока и сопротивления проводника, можно записывать закон Джоуля-Ленца более упрощенно:
$Q = I^2Rt$
Применяя закон Ома в совокупности с алгебраическими преобразованиями, получаем следующие эквивалентные формулы:
$Q = \frac{U^2t}{R} = UIt$
Исследования физиков Джоуля и Ленца относительно тепловыделения от действия электрического тока значительно продвинули научное понимание определенных физических процессов, а выведенные при этом основные формулы, не претерпев изменений, продолжают активно использоваться в различных научно-технических отраслях.
Готовые работы на аналогичную тему
Курсовая работа Теплота и энергия в электрической цепи 490 ₽ Реферат Теплота и энергия в электрической цепи 280 ₽ Контрольная работа Теплота и энергия в электрической цепи 200 ₽
Получить выполненную работу или консультацию специалиста по вашему учебному проекту Узнать стоимость
В сфере электротехники выделяют несколько технических задач, где количество теплоты, которая будет выделяться при протекании тока, имеет критически важное значение при расчете таких параметров, как:
- теплопотери в ЛЭП;
- характеристики для проводов сетей электропроводки;
- тепловая мощность электронагревателей;
- температура срабатывания автовыключателей;
- температура плавления плавких предохранителей;
- тепловыделение разных электротехнических аппаратов, а также элементов радиотехники.
Замечание 2
Тепловое действие электротока в проводах ЛЭП является нежелательным из-за весомых потерь электроэнергии на тепловое выделение. Согласно различным данным, в ЛЭП теряется до 40% всей производимой в мировом формате электрической энергии. С целью сокращения потерь в процессе передачи электроэнергии на большие расстояния, напряжение в ЛЭП поднимают (с произведением расчетов на основании производных формул закона Джоуля-Ленца).
Электрическая энергия и мощность
Nbsp; Вопросы к зачету. 1. Электрическая цепь. Определение. Основные элементы электрической цепи. Виды энергии. Основные условные графические обозначения элементов и проводников. 2. Классификация электрических цепей. 3. Основные явления в электрической цепи и величины, их характеризующие (Физические процессы в электрической цепи. Электродвижущая сила. Электрический ток, Напряжение, Потенциал и разность потенциалов, сопротивление, проводимость.) 4. Закон Ома. Внутренние сопротивление источника. Обобщающий закон Ома. 5. Закон Кирхгофа. 6. Энергия и мощность в электрической цепи. 7. Источники электрической энергии. 8. Распределение потенциала вдоль неразветвленной электрической цепи. 9. Источники электрической энергии. 10. Метод преобразования цепи. Применение метода. Преобразование последовательно соединенных резисторов или резистивных элементов. 11. Преобразование параллельно соединенных резисторов или резистивных элементов. 12. Метод непосредственного применения законов Кирхгофа (Законы Кирхгофа, Порядок расчета). 13. Метод узловых потенциалов. 14. Принцип и метод наложения. 15. Метод эквивалентного генератора. 1.Электрическая цепь — это совокупность электротехнических устройств, объектов (источников, приемников электроэнергии, коммутационных, защитных аппаратов и пр.) и соединяющих их проводников, представляющих собой путь для прохождения электрического тока. Происходящие в электрических цепях (далее — ЭЦ) процессы передачи, распределения или преобразования электроэнергии могут быть описаны с использованием понятий об ЭДС, напряжении и силе тока.Протекание электрического тока возможно только в замкнутой ЭЦ; при ее размыкании на любом участке протекание тока прекратится. Активные и пассивные элементы электрической цепи Элементы, входящие в состав электрических цепей, могут быть активными и пассивными. Основным признаком активных составляющих, считается их способность отдавать электроэнергию. Типичными представителями являются генераторы и другие источники электроэнергии, усилители электрических сигналов и другие. Пассивными элементами считаются различные виды потребителей и накопителей электрической энергии. К ним относятся конденсаторы, резисторы, катушки индуктивности и другие двухполюсные устройства. Существует многополюсная аппаратура, функционирующая на базе двухполюсных элементов. Все активные элементы электрической цепи могут быть независимыми и зависимыми. В первую категорию входят источники напряжения и тока. В свою очередь, источник напряжения считается идеализированным элементом цепи, у которого напряжение на зажимах не зависит от протекающего через него электрического тока, а внутреннее сопротивление имеет нулевое значение. Источник тока также является безупречным элементом, у которого ток не зависит от напряжения на зажимах, а значение внутреннего сопротивления стремится к бесконечности. Зависимые источники напряжения и тока именуются таковыми, когда эти величины зависят от параметров напряжения и тока на другом участке цепи. Типичными представителями являются электролампы, транзисторы, усилители, функционирующие в линейном режиме. Основные пассивные элементы электрической цепи представлены резисторами, индуктивными катушками и конденсаторами, с помощью которых регулируются параметры тока и напряжения на отдельных участках. Резистивное сопротивление относится к идеализированным элементам цепи. Его основным свойством является необратимое рассеивание энергии. Зависимость напряжения и тока резистивного сопротивления выражается формулами: u = iR, i = Gu, в которых R является сопротивлением, измеряемым в Омах, а G – проводимостью, измеряемой в сименсах. Соотношение этих величин между собой выражено формулой R = 1/G. Идеализированные индуктивные элементы цепи способны накапливать энергию магнитного поля. Основным параметром считается линейная индуктивность, находящаяся в линейной зависимости между магнитным потоком и током, графически представляющая собой вебер-амперную черту. Индуктивность является также и коэффициентом пропорциональности, измеряемом в Генри. Ёмкостные элементы – конденсаторы обладают свойством накапливать энергию электрического поля. Показатель линейной емкости представляет собой линейную зависимость между зарядом и напряжением, выраженной формулой q = Cu. Условные обозначения элементов электрической цепи Для удобства анализа и расчетов электрических цепей, все их составляющие отображаются в виде специальных схем. Данные схемы состоят из условных обозначений используемых элементов и способов их соединения. Условные обозначения в странах СНГ могут отличаться от символики, принятой в других государствах, соответственно, будут различаться и сами схемы, поскольку использовались различные системы графических маркировок. Все элементы на схемах условно разделяются на три группы: К первой относятся источники питания, преобразующие другие виды энергии в электрическую. В этом случае они считаются первичными. Ко вторичным источникам относятся, например, выпрямительные устройства, у которых электроэнергия имеется на входе и на выходе. Вторая группа представлена потребителями энергии, преобразующими электрический ток в тепло, освещение, движение и т.д. В третью группу входят управляющие элементы, без которых невозможна работа любой цепи. Сюда входят соединительные провода, коммутационная аппаратура, измерительные приборы и другие устройства аналогичного назначения. Все эти составляющие охвачены единым электромагнитным процессом, поэтому они включаются в общую схему с использованием специальных условных знаков. Следует учитывать, что вспомогательные элементы могут не указываться на схемах. Не указываются и соединительные провода, если их сопротивление значительно ниже, чем у составных элементов. Источники питания обозначаются в виде электродвижущей силы. При необходимости проставляются пояснительные надписи. 2. Классификация электрических цепей По типу сложности: простые (неразветвленные), сложные (разветвленные);По виду тока: переменного и постоянного тока;По составу элементов: активные, пассивные, линейные, нелинейные цепи;По характеру распределения параметров: цепи с сосредоточенными и распределенными параметрами;Цепи переменного тока делятся по числу фаз: однофазные, многофазные.Электрические цепи рассчитывают. Для облегчения расчетов составляется схема замещения электрической цепи, т.е. схема, отображающая свойства цепи при определенных условиях. На схеме замещения изображают все элементы, влиянием которых на результат расчета пренебречь нельзя, и указывают все электрические соединения между ними.Любая электрическая цепь может быть представлена в виде схемы с помощью условных графических обозначений. Условные обозначения установлены стандартами системы ЕСКД.Электрические цепи могут иметь последовательное или параллельное соединение электрических элементов. Любой элемент имеет вход (начало) или выход (конец). При последовательном соединении элементов выход предыдущего элемента всегда соединяется с входом последующего элемента. В электрических цепях с последовательным соединением ток во всех элементах одинаковый, а напряжение на каждом элементе зависит от величины его сопротивления. При параллельном соединении элементов объединяются входы нескольких элементов в один узел, а выходы этих элементов включаются в другой узел. При параллельном соединении элементов напряжение на всех элементах будет одинаковым, а величина тока в ветвях будет зависеть от их сопротивления. 4.Зако́н О́ма — эмпирический физический закон, определяющий связь электродвижущей силы источника (или электрического напряжения) с силой тока, протекающего в проводнике, и сопротивлением проводника Внутреннее сопротивление источника тока — количественная характеристика источника тока, которая определяет величину энергетических потерь при прохождении через источник электрического тока. Внутреннее сопротивление имеет размерность сопротивления и измеряется в Омах. При прохождении электрического тока через источник происходят те же процессы диссипации энергии, и при прохождении через сопротивление нагрузки. Благодаря этим процессам напряжение на клеммах источника тока не равна электродвижущей силе, а зависит от величины тока, а, следовательно, от нагрузки. При небольших значениях силы тока эта зависимость линейная и ее можно представить в виде , где U — напряжение, — Электродвижущая сила, R i — внутреннее сопротивление. Таким образом, каждый источник электрического тока характеризуется своим внутренним сопротивлением, который необходимо учитывать при расчете электрических цепей.
Обобщенный закон Ома.
Закон Ома выражаемый формулой , определяет зависимость между током и напряжением на пассивном участке электрической цепи.
Определим зависимость между током, напряжением и э.д.с. на активном участке (рис. 16).
Из формулы 15 следует:
ja -jb=I(R1+R2)- E1+E2 (16)
На положительное напряжение на участке a – b Uab=ja -jb
Следовательно, Uab= I(R1+R2)- E1+E2 (17)
(18)
Формула (18) выражает обобщенный закон Ома, или закон Ома для участка, содержащего э.д.с.
Из формулы видно, что если ток, напряжение и э.д.с. совпадают по направлению, то в выражение закона Ома они входят с одинаковыми знаками. Если э.д.с. действует в сторону, противоположную положительному направлению тока, то в выражении ставится знак «-».
Закон Ома применяется для участка ветви и для одноконтурной замкнутой схемы.
5. Первый закон Кирхгофа показывает связь токов и узлов электрической цепи. Формула связи очень проста. Это правило гласит, что сумма токов всех ветвей, которые сходятся в один узел электроцепи, равняется нулю (речь идёт об алгебраических значениях).
При этом накопление электрических зарядов в одной точке замкнутой электроцепи невозможно. При суммировании токов принято брать положительный знак, если электроток идёт по направлению к узлу, и отрицательный знак, если ток идёт в противоположную от узла сторону. Для описания понятной аналогии для этого случая, уместны сравнения с течениями воды в соединенных между собой трубопроводах.
Второй закон Кирхгофа описывает алгебраическую зависимость между электродинамической силой и напряжением в замкнутой электроцепи. В любом замкнутом контуре сумма электродинамической силы равна сумме падания напряжения на сопротивлениях, относящихся к данному контуру.
Для написания формул, определяющих второй закон Кирхгофа, берут положительное значение электродинамической силы и падение напряжений, если направление на относящихся к ним отрезках контура совпадает с произвольным направлением обхода контура. А если же направление электродинамической силы и токов противоположны выбранному направлению, то эти электродинамические силы и падение напряжений берут отрицательными:
Электрическая энергия и мощность
В любой электрической цепи электрическая энергия (а также мощность) вырабатываемая источниками, равна энергии (мощности), потребляемой приемниками.
Согласно закону Джоуля — Ленца энергия, потребляемая резистивным элементом (резистором) с сопротивлением R, определяется по формулам:
W = I2 Rt
(2.14)
W=UIt.
В электрической цепи постоянного тока мощность P
равна отношению энергии
W
к промежутку времени
t
, в течение которого энергия была выработана источником или преобразована приемником электрической энергии.
,
(2.15)
Мощность численно равна энергии W
, если промежуток времени
t
равен единице.
Из (2.14) и (2.15) получаем выражения для расчета мощности резистивного приемника:
(2.16)
Рпр = UI
.
Если направление ЭДС и тока через источник совпадают, то мощность, вырабатываемая источником с ЭДС Е
равна:
Рu
=
E·I.
В противном случае мощность источника отрицательна
Рu
= —
E·I.
и ее относят к мощности приемника.
Для любой электрической цепи можно записать уравнение баланса мощностей
Рu
=
Pn,
или
ΣEiIi
= Σ
Ii2Ri
(2.17)
В левой части уравнения (2.17) находятся мощности, вырабатываемые всеми источниками электрической энергии, в правой — мощности, преобразуемые (потребляемые) всеми приемниками электрической энергии.
Основными единицами электрической энергии (ЭЭ) и мощности являются 1 джоуль (1 Дж=1 ВАс) и 1 ватт (1 Вт=1 Дж/с=1 ВА). Для мощности и энергии промышленных установок часто используются более крупные единицы: 1 киловатт (1 кВт=103 Вт), 1 мегаватт (1 МВт=106 Вт), 1 киловатт-час (1 кВтч=3,6 106 Втс).
Расчеты потерь электроэнергии в линии электропередач
Как пример, гипотетически берется участок ЛЭП от электростанции до трансформаторной подстанции. По причине того, что провода ЛЭП и потребитель электрической энергии (трансформаторная подстанция) соединены последовательным образом, через них будет течь один и тот же ток $I$. Тогда, на основании закона Джоуля – Ленца, количество теплоты $Q_w$, которая выделится на проводах, рассчитывают, согласно формуле:
$Q_w = R_wI^2$
Производимая электротоком мощность $Q_c$ в нагрузке определяется на основании закона Ома:
$Q_с = U_сI$
При условии равенства токов, таким образом, в первую формулу вместо $I$ вставляется выражение $\frac{Q_c}{U_c}$:
$Q_w = \frac{R_wQ_c^2}{U_c^2}$
При условии игнорирования зависимости сопротивления проводников от изменения температуры, $R_w$ можно считать неизменной величиной (константой). При стабильном энергопотреблении потребителя (трансформаторной подстанции), таким образом, выделение тепловой энергии в проводах ЛЭП будет считаться обратно пропорциональным квадрату напряжения в конечной точке линии. Иными словами, чем больше окажется напряжение электропередачи, тем меньшими станут потери электроэнергии.
Электрический ток и нагрузка
В дело идет Закон Ома. Как я уже писал, это самый значимый закон во всей электронике. Что такое по сути лампочка? Это вольфрамовый проводок в стеклянной колбе с вакуумом. Вольфрам — это металл, следовательно, он может через себя проводить электрический ток. Но весь прикол в том, что при определенном напряжении он раскаляется и начинает светиться. То есть отдавать энергию в пространство в виде тепла и излучения.
В холодном состоянии вольфрамовая нить обладает меньшим сопротивлением, чем в раскаленном, более чем в десять раз. Следовательно, лампочка — это просто как сопротивление для электрической цепи. В этой статье я взял лампочку, чтобы визуально показать нагрузку. Нагрузка — от слова «нагружать». Источнику питания не нравится, когда ему приходится отдавать электроэнергию. Он любит работать без нагрузки
Теперь давайте представим все это с точки зрения гидравлики и механики.
Имеем трубу, по которой бурным поток течет вода. К трубе приделана вертушка, типа водяного колеса. Лопасти вертушки крутят вал.
Рисунок я чертил по всем догмам черчения: главный вид, и справа его разрез.
Если к валу ничего не цепляется, то поток воды бурно бежит по трубе и крутит колесо, а оно в свою очередь крутит вал. Такой режим можно назвать холостым режимом работы водяного колеса, то есть режимом без нагрузки.
Но что будет, если мы начнем использовать вращение вала себе во благо? Например, соединим с помощью муфты вал водяного колеса с валом мини-мельницы?
Думаю, многие из моих читателей сразу догадаются, что водяное колесо начнет притормаживать, так как мы его заставили работать. Крутиться со скоростью холостого хода у нашего вала уже не получится. Скорость будет меньше. То есть в нашем случае у нас на валу есть нагрузка. Что же будет происходить с потоком воды в трубе? Он будет тормозиться, так как лопасти вала не дадут водичке спокойно бежать по трубе. Поэтому, общий поток воды в трубе будет меньше, чем ДО холостого хода вала.
А если нагрузить вал, чтобы тот поднимал грузовой лифт?
Думаю, вся конструкция тут же встанет колом. То есть большая нагрузка станет непосильна для вала. А если бы мы сделали лопасти вертушки такие, чтобы они полностью перекрывали диаметр трубы, то поток жидкости вообще бы остановился.
Давайте разберем еще один пример для понимания. Все тот же самый рисунок:
Предположим, что мы прицепили к валу наждак, а электродвигатель убрали с этой конструкции. И вот мы решили что-нибудь шлифануть.
Итак, что у нас в результате получается? Если мы будем слабо давить на шлифовальный круг, то у нас круг начнет притормаживаться и уже будет крутиться с другой скоростью. Если мы сильнее будем давить на круг, то скорость вала еще больше упадет. Если же мощность нашего вала слабовата, мы можем добиться того, что при сильном давлении на круг вообще остановить вал. Тогда и точиться ничего не будет…
Давайте снова вернемся к мини-мельнице
Что будет если поток воды в трубе увеличить в несколько раз? Мельница будет крутиться так, что ее порвет нахрен! А если поток воды в трубе будет очень слабый? Разумеется, мельница будет молоть одно-два зернышка в час. Хотя, опять же, с большим потоком воды мы вполне можем поднять лифт.
Понимаете к чему я веду? Все завязано друг с другом! Давление в трубе, скорость потока жидкости и нагрузка… Все они связаны воедино.