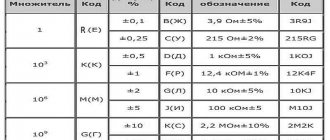
Правила работы на калькуляторе
В быту нас интересуют, как правило, четыре взаимосвязанных характеристики электричества:
- напряжение;
- ток;
- сопротивление;
- или мощность.
Если тебе известны две величины, входящие в закон Ома (U, R, I), то вводи их в соответствующие строки, а оставшийся параметр и мощность будут вычислены автоматически.
Будь внимательным, чтобы не допустить ошибки.
Все значения надо заполнять в одной размерности: амперы, вольты, омы, ватты без использования обозначений дольности или кратности.
Осуществить переход к ним тебе поможет наглядная таблица.
Назначение и определение импеданса
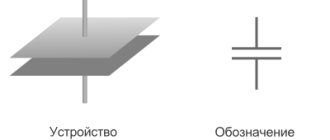
Практически ни одно электронное устройство не обходится в своей схеме без резисторов. Являясь пассивными элементами, они имеют основное предназначение — ограничивать величину тока в электрической цепи. Кроме токоограничения, они служат делителями напряжения или шунтами в измерительных приборах.
Электрическое сопротивление — это величина, имеющая физическую природу и характеризующая возможность проводника пропускать электрический ток. Принцип работы резистора был описан выдающимся экспериментатором Омом. Позже в его честь и была названа единица измерения электрического сопротивления — Ом. Учёный, проводя ряд экспериментов, установил зависимость между силой тока, напряжением и сопротивлением в проводнике. В результате была выведена простая формула, известная как закон Ома: I = U/R, где:
- I — проходящая через проводник сила тока, измеряемая в Амперах;
- U — напряжение, приложенное к проводнику, единица измерения — Вольт;
- R — сопротивление проводника, измеряется в Омах.
Позже устройства, использующиеся только в качестве элементов сопротивления в электрических цепях, получили название — резисторы. Такие приборы, кроме величины сопротивления, характеризуются мощностью, рассчитывающейся по следующей формуле: P = I2 * R. Полученная величина измеряется в Ваттах.
В схемотехнике используется как параллельное, так и последовательное соединение проводников. В зависимости от этого изменяется и величина импеданса участка цепи. Вид соединения, если он не используется для подбора нужного значения, как раз и характеризует применение резисторов в первом случае как токоограничителей, а во втором — как делителей напряжения.
На схемах резисторы обозначаются в виде прямоугольника и подписываются латинской буквой R. Рядом указывается порядковый номер и значение сопротивления. Например, R23 1k обозначает, что резистор с номером 23 имеет сопротивление, равное одному килоОму. Полоски, изображённые внутри прямоугольника, характеризуют мощность, рассеиваемую на проводнике.
Фундаментальный закон сохранения энергии гласит: энергия никуда не исчезает и из ниоткуда не появляется, а только изменяет форму. Поэтому при ограничении тока часть энергии трансформируется в тепло. Именно эту часть и называют мощностью рассеивания резистора, т. е. такую её величину, которую может выдержать сопротивление без изменения своих параметров.
Сам по себе резистор может иметь различную конструкцию и вид. Например, быть проволочным, керамическим, слюдяным и т. п. Маркируется он тремя способами:
- Цветной полосочной системой. Каждая полоска отвечает за определённый множитель. Расшифровку полосок можно взять из справочников или онлайн-калькуляторов.
- Цифрами и буквами. Число указывает непосредственно значение сопротивления, а буква — множитель. Например,15M — пятнадцать мегаОм.
- Цифровая. Обычно используются три цифры, первая и вторая обозначают значение сопротивления, а последняя — множитель. Например, 103 — десять килоОм.
Поэтому видя, какие резисторы установлены в схеме, даже начинающему радиолюбителю не составит труда рассчитать общее сопротивление, особенно используя онлайн-калькулятор параллельного соединения резисторов или последовательного. В случае невозможности различить маркировку на корпусе его сопротивление возможно измерить мультиметром. Но опытные электротехники знают, что для точного измерения понадобится один вывод сопротивления отсоединить от схемы. Связано это как раз с видом подключения проводника.
Простые примеры расчета
Бытовая сеть переменного тока
Пример №1. Проверка ТЭНа.
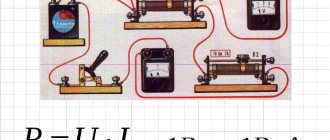
В стиральную машину встроен трубчатый электронагреватель 1,25 кВт на 220 вольт. Требуется проверить его исправность замером сопротивления. По мощности рассчитываем ток и сопротивление.
I = 1250 / 220 = 5,68 А; R = 220 / 5,68 = 38,7 Ом.
Проверяем расчет сопротивления калькулятором по току и напряжению. Данные совпали. Можно приступать к электрическим замерам.
Пример №2. Проверка сопротивления двигателя
Допустим, что мы купили моющий пылесос на 1,6 киловатта для уборки помещений. Нас интересует ток его потребления и сопротивление электрического двигателя в рабочем состоянии. Считаем ток:
I = 1600 / 220 = 7,3 А.
Вводим в графы калькулятора напряжение 220 вольт и ток 7,3 ампера. Запускаем расчет. Автоматически получим данные:
- сопротивление двигателя — 30,1 Ома;
- мощность 1600 ватт.
Цепи постоянного тока
Рассчитаем сопротивление нити накала галогенной лампочки на 55 ватт, установленной в фаре автомобиля на 12 вольт.
Считаем ток:
I = 55 / 12 = 4,6 А.
Вводим в калькулятор 12 вольт и 4,6 ампера. Он вычисляет:
- сопротивление 2,6 ома.
- мощность 5 ватт.
Здесь обращаю внимание на то, что если замерить сопротивление в холодном состоянии мультиметром, то оно будет значительно ниже.
Это свойство металлов позволяет создавать простые и относительно дешевые лампы накаливания без сложной пускорегулирующей аппаратуры, необходимой для светодиодных и люминесцентных светильников.
Другими словами: изменение сопротивления вольфрама при нагреве до раскаленного состояния ограничивает возрастание тока через него. Но в холодном состоянии металла происходит бросок тока. От него нить может перегореть.
Для продления ресурса работы подобных лампочек используют схему постепенной, плавной подачи напряжения от нуля до номинальной величины.
В качестве простых, но надежных устройств для автомобиля часто используется релейная схема ограничения тока, работающая ступенчато.
При включении выключателя SA сопротивление резистора R ограничивает бросок тока через холодную нить накала. Когда же она разогреется, то за счет изменения падения напряжения на лампе HL1 электромагнит с обмоткой реле KL1 поставит свой контакт на удержание.
Он зашунтирует резистор, чем выведет его из работы. Через нить накала станет протекать номинальный ток схемы.
Где применяется делитель тока
Делитель тока очень часто встречается в электротехнике. Важно не путать делитель тока с делителем напряжения, так как после анализа общедоступных источников была выявлена противоречивая информация даже в википедии.
Цитирование из википедии: «Делитель тока имеет важное значение в схемотехнике в качестве элемента цепи для подключения устройства с номинальным током меньшим, чем протекающий в цепи.» Цитирование из другого источника: «При проектировании электрических цепей возникают случаи, когда в цепи протекает ток одного номинала, а номинально-допустимый ток нагрузки должен быть меньше. Для этих целей используют делители тока.» А вот к чему все это приводит — цитирование очередного электротехнического блога: «Проще говоря, если вместо одного из резисторов подключить, например, вентилятор, то изменяя сопротивление второго резистора, мы будем также изменять силу тока, а значит и мощность, проходящую через вентилятор.»
Важно понимать, что напряжение во всей цепи одинаково для каждого резистора. И сила тока на участке резистора зависит только от его сопротивления. Поэтому, если рассмотреть пример с вентилятором, изменяя сопротивление другого резистора, мы не можем изменить силу тока, проходящую через вентилятор. Мощность останется прежней. Чтобы изменить силу тока и соответственно мощность, вместе с вентилятором должна быть последовательно соединена нагрузка, а не параллельно. Последовательное соединение — это делитель напряжения. Параллельное соединение — это делитель тока. Информацию из википедии трудно назвать неверной, но она не полная. Там не хватает уточнения, что для подключения устройства с номинальным током меньшим, чем протекающий в цепи, нужно совмещать делитель тока с делителем напряжения.
Вернемся к примерам использования делителя тока. Цепи делителей тока находят применение в измерительных схемах, где требуется, чтобы часть измеряемого тока проходила через чувствительный прибор. Используя формулу делителя тока, можно подобрать подходящий шунтирующий резистор таким образом, чтобы через измерительный прибор всегда проходила точно заданная доля общего тока:
Теперь обратимся к примерам делителя тока, которые буквально рядом с каждым. Любой частный дом или квартира — это параллельное соединение, соответственно и делитель тока. Совокупность всех повторных заземлителей нейтрали трансформатора — это тоже делитель тока. А не самый приятный пример параллельного соединения — это ситуация, когда ток одновременно уходит через заземлитель и человека, прикоснувшегося к корпусу заземленного электроприбора. В этом случае заземлитель с небольшим сопротивлением в сумме с большим сопротивлением человека дает общее небольшое сопротивление. Можно даже не считать, а просто воспользоваться одним из правил — общее сопротивление всегда меньше сопротивления любого параллельно включенного резистора. И здесь важно понимать, что ток, проходя эту связку заземлитель-человек, далее на своем пути встречает еще одно сопротивление — например от заземлителя нейтрали трансформатора. Получается делитель напряжения, который в совокупности с делителем тока и является основой безопасности использования заземления. То есть на каждом заземлителе происходит падение напряжения. А чем меньше напряжение, тем меньше сила тока.
Полезная информация для начинающего электрика
Как использовать закон Ома на практике
Почти два столетия назад в далеком 1827 году своими экспериментами Георг Ом выявил закономерность между основными характеристиками электричества.
Он изучил и опубликовал влияние сопротивления участка цепи на величину тока, возникающего под действием напряжения. Ее удобно представлять наглядной картинкой.
Любую работу всегда создает трудяга электрический ток. Он вращает ротор электрического двигателя, вызывает свечение электрической лампочки, сваривает или режет металлы, выполняет другие действия.
Поэтому ему необходимо создать оптимальные условия: величина электрического тока должна поддерживаться на номинальном уровне. Она зависит от:
- значения приложенного к цепи напряжения;
- сопротивления среды, по которой движется ток.
Здесь напряжение, как разность потенциалов приложенной энергии, является той силой, которая создает электрический ток.
Если напряжения не будет, то никакой полезной работы от подключённой электрической схемы не произойдёт из-за отсутствия тока. Эта ситуация часто встречается при обрыве, обломе или отгорании питающего провода.
Сопротивление же решает обратную для напряжения задачу. При очень большой величине оно так ограничивает ток, что он не способен совершить никакой работы. Этот режим применяется у хороших диэлектриков.
Калькулятор делителя тока онлайн
Представленный онлайн-калькулятор позволяет рассчитать силу тока при использовании последовательных резистивных делителей на любом участке цепи. Для расчета необходимо ввести общую силу тока цепи и значения сопротивлений резисторов на параллельном участке. Калькулятор делителя тока поддерживает до 10 резисторов одновременно.
Калькулятор делителя тока на резисторах:
| Сила тока источника, А | |
| Резистор | Сила тока на участке резистора, А |
Определение
Если посчитать общее сопротивление (Rобщ), можно выяснить изменение основных электрических параметров (тока (I) и напряжения (U)) при подключении схемы к определенному источнику питания. В простейшем варианте достаточно применить закон Ома (I = U/ R) и пренебречь внутренним сопротивлением аккумулятора.
При напряжении U = 6,5 В через подключенный резистор R = 20 ОМ будет проходить ток I = 6,5/20 = 0,325 А. По вычисленному параметру с помощью классической формулы можно узнать мощность:
P = I2 *R = U2/ R = 0,105625 * 20 = 2,11 Вт.
Полученное значение пригодится для выбора подходящего пассивного элемента в ассортименте магазина.
На практике приходится решать задачи с большим количеством элементов. Общий показатель эквивалентен суммарному сопротивлению цепи. Однако простым сложением правильный результат получить нельзя. Ниже рассмотрены технологии, по которым выполняют корректные вычисления.
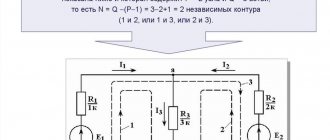
Рисунок поясняет используемую терминологию:
- i1, i2… i6 – токи в отдельных цепях;
- R1-R3 – пассивные элементы (резисторы);
- e1, e2 – типичные обозначения источников тока (ЭДС);
- L и C – компоненты с реактивными характеристиками (индуктивными и емкостными, соответственно);
- ветвями называют с одним током;
- места соединение этих цепей – узлы;
- контуры (обозначены римскими цифрами I, II и III) показывают замкнутые пути прохождения токов по нескольким ветвям.
Как определить эквивалентное сопротивление
Если в электрической сети находится несколько резистивных источников, то, чтобы подсчитать силу тока, напряжения и мощность, следует использовать один взаимозаменяемый физический показатель сопротивления электрической цепи.
Любой показатель последовательного или параллельного подключения возможно преобразовать, используя эквивалентный резистор и один источник электродвижущей силы. Сопротивляемость в данном случае будет равна сумме всех препятствий пассивных устройств заряду электрической сети. Электродвижущая сила взаимозаменяемого источника будет равна сумме всех источников, которые входят в цепь.
Формула определения показателя
Обратите внимание! Сворачиванием цепи, используя преобразования последовательно подключенных или параллельных проводниковых приборов, можно по максимуму сделать проще дальнейший расчет в любой схеме. Исключением будут выступать цепи, которые содержат сопротивляемость по схеме в виде звезды и треугольника.
Что такое эквивалентное сопротивление резисторов
Точного понятия в физике не существует. Его можно вывести через ряд других терминов и формулировку закона Ома. В результате получится, что эквивалентное сопротивление резисторов — это суммарное препятствие взаимозаменяемых пассивных элементов электрической сети, чтобы заряд проходил в проводник.
Сопротивляемость резисторов
К сведению! Один показатель дает на выходе значение сопротивляемости без воздействия на него ряда посторонних моментов.
Подробное объяснение эквивалентному сопротивлению
Параллельное соединение
Такое соединение резисторов получается путём объединения двух и более электрических устройств, при котором их одни выводы соединяются друг с другом и образовывают первую общую точку, а другие, аналогично первым, образовывают вторую общую точку. В этом случае напряжение на всех элементах одинаковое, а проходящая сила тока зависит от их импеданса.
Формула параллельного соединения резисторов выглядит следующим образом:
Какое освещение Вы предпочитаете
ВстроенноеЛюстра
R = (R1*R2*R3…*Rх) / (R1+R2+R3…+Rх), где Rх – порядковый номер резистора.
Отсюда следует, что сила тока, протекающая через каждый проводник, находится по формуле: In = U/Rn.
Исходя из этого, при параллельном соединении результирующий импеданс двух и более резисторов будет меньше самого меньшего значения сопротивления в соединении. При этом когда параллельно включены только два резистора, имеющие одинаковый номинал, то их можно заменить эквивалентом, равным одной второй от величины этого номинала.
Так можно соединить и сотню резисторов, тогда эквивалентное сопротивление определяется как сотая часть от номинала. Например, пусть будет участок схемы с десятью резисторами, включёнными параллельно друг другу с номиналом каждого равного 10 Ом, тогда общее сопротивление будет составлять десятую часть, а именно Rоб = 10/10 = 1 Ом.
Важно отметить, что при таком соединении величина тока поделится на каждый элемент, поэтому и резисторы можно применить меньшей мощности, чем если бы использовался эквивалент, заменяющий всё параллельное подключение.
Пример подбора замены
При разработке прибора возникла потребность использовать на участке цепи резистор с сопротивлением 6 Ом. При изучении номинального ряда стандартных значений, выпускаемых промышленностью, можно отметить, что резистора на 6 Ом в нём нет.
Для получения нужного значения понадобится воспользоваться параллельным включением двух элементов. Эквивалентное значение сопротивления для двух резисторов в таком случае находится в следующем порядке:
- 1/R = (1/R1) + (1/R2);
- 1/R = (R1+R2) / (R1*R2);
- Rэ = (R1*R2) / (R1+R2).
Из решения видно, что если R1 совпадает по номиналу с R2, то общая величина сопротивления равна половине значения одного из элементов. Поэтому при требуемом номинале, равном 6 Ом, это значение составит: Rx = 2*6 = 12 Ом. Для проверки результата следует подставить полученный ответ в формулу: Rэ = (R1*R2) / (R1+R2) = (12*12) / (12+12) = 6 Ом.
Таким образом, решением поставленной задачи будет параллельное включение двух резисторов с величиной сопротивления, равной 12 Ом.
Задача на нахождение эквивалента
Пусть существует схема с тремя параллельно включёнными резисторами и для её упрощения необходимо заменить их одним элементом. Номиналы проводников составляют: R1 = 320 Ом, R2= 10 Ом, R3 = 1 кОм. Для решения задачи используется уже известная формула:
- 1/R = (1/R1) + (1/R2) + (1/R3);
- Rэкв = (R1*R2*R3) / (R1+R2+R3).
Перед тем как подставлять величины в формулу, их все понадобится привести к международной системе единиц (СИ). Так, один килоОм равен 1000 Ом, при подставлении этого значения получается ответ: Rэ = (320*1*1000) / (320+10+1000) = 2406 Ом или 2,4 кОм, что как раз соответствует величине из стандартного ряда. Такая методика расчёта применяется для любого количества параллельно соединённых резисторов.
Цветовая маркировка резисторов с пятью и шестью полосками онлайн расчет
Калькулятор резисторов с пятью цветными полосками:
Для определения сопротивления у резисторов с шестью полосами нужно использовать калькулятор элементов с пятью полосками и учесть шестую цветную полосу, которая означает температурный коэффициент сопротивления. Подробная таблица значений температурного коэффициента сопротивления (ТКС) и их привязка к конкретному цвету приведена в следующей таблице:
| Цвет | ТКС (ppm/ºC) |
| Коричневый | 100 |
| Красный | 50 |
| Желтый | 25 |
| Оранжевый | 15 |
| Голубой | 10 |
| Фиолетовый | 5 |
| Белый | 1 |
Смешанное подключение
В этом случае на участке схемы используется комбинация параллельного и последовательного включения элементов. Такое соединение часто называется параллельно-последовательным:
- При последовательном включении общий импеданс элементов прямо пропорционален сумме сопротивлений каждого из резисторов.
- При параллельном включении проводников значение, обратное сумме импеданса цепи, соответствует сумме значений, обратных сопротивлениям параллельно включённых элементов.
Используя эти правила, которые справедливы для любого числа соединённых проводников в схеме, определяется общее значение импеданса для любого вида подключения. Для того чтобы определить эквивалентное значение сопротивления параллельно-последовательного соединения, участок схемы делится на небольшие группы из параллельно или последовательно включённых резисторов. Затем используется алгоритм, помогающий оптимально посчитать значение эквивалента:
Определяется общее сопротивление всех узлов в схеме с параллельным подключением резисторов:
- При нахождении в этих узлах последовательно соединённых проводников первоначально считается их сопротивление.
- Как только значения эквивалентных значений вычислены, схема упрощается до последовательной цепочки из эквивалентных резисторов.
- Находится окончательное значение общего сопротивления.
Например, существует схема, в которой надо определить полное сопротивление цепи, при этом сопротивление резисторов R1=R3=R5=R6=3 Ом, а R2 =20 Ом и R4=24 Ом. Сопротивления R3, R4, и R5 включены последовательно, поэтому общий импеданс на этом участке цепи равен: Rоб1 = R3+R4+R5 = 30 Ом.
После замены R3, R4, R5 на Rоб1 резистор R3 окажется подключённым параллельно этому сопротивлению. Поэтому импеданс на этом участке будет равен:
Rоб2 = (R2* Rоб1) / (R3+Rоб1) = (20*30) / (20+30) = 12 Ом.
Резисторы R1 и R6 включены с Rоб2 последовательно, а это значит, что эквивалент всей схемы равен: Rэкв = Rоб1+Rоб2+ R6 = 3+12+3 = 18 Ом.
Так шаг за шагом вычисляется эквивалентное значение любой сложности схемы. При множестве проводников, входящих в электрическую цепь, нетрудно ошибиться при расчётах, поэтому все операции выполняются аккуратно или используются онлайн-калькуляторы.