Катушка индуктивности в цепи переменного тока – принцип действия и значение

Теоретика

Для начала давайте определим назначение этой детали, а также основные понятия и термины, связанные с ней.

Что такое катушка индуктивности

Катушка индуктивности – это радиоэлемент, применяющийся в разных схемах для следующего:

• Сглаживание биений;
• Подавление помех;
• Ограничение переменного тока;
• Накопление энергии и прочее.

Представляет собой данный элемент спиральную, винтовую или винтоспиральную катушку, сделанную из изолированного проводника. Деталь обладает относительно малой емкостью и малым активным сопротивлением, при этом у него имеет высокая индуктивность, то есть способность возникновения ЭДС (электродвижущей силы) в проводнике, при протекании в цепи электрического тока.

• Катушка индуктивности, в зависимости от места и цели применения может иметь и другие названия. Например, если элемент используется для изоляции по высокой частоте в разных частях схемы, накоплении энергии магнитного поля сердечника, сглаживания пульсаций и подавления помех, катушку называют дросселем либо реактором (второе название употребляется редко).
• Если говорить про силовую электротехнику, то там устоялось название ректор – его применяют при необходимости ограничения тока, например, если произошло замыкание на ЛЭП.

• Бывают также и цилиндрические катушки индуктивности, называемые соленоидами. Длина такого цилиндра в несколько раз превышает его диаметр.

Интересно знать! Магнитное поле внутри соленоида однородно. Данное магнитное поле может выполнять механическую работу, втягивая ферритовый сердечник.

• Применяются катушки индуктивности и в электромагнитных реле, где их называют обмоткой реле.
• Устанавливаются подобные элементы и в индукционные нагреватели – тут их называют нагревательными индукторами.

• Также можно услышать термины вроде индукционного накопителя или накопительного дросселя, если речь идет об устройствах импульсной стабилизации напряжения.

Конструкционные особенности

Конструкционно катушка индуктивности представляет собой намотанную по спирали или винтом изолированную одножильный или многожильный проводник (чаще, лакированная медная проволока), вокруг диэлектрического сердечника (каркаса). Форма сердечника может быть круглой, тороидальной, прямоугольной, квадратной. Материалы, применяемые для сердечника, имеют магнитную проницаемость выше, чем у воздуха, что дополнительно удерживает магнитное поле возле катушки, а значит, увеличивается и индуктивность.

Существуют и катушки, вовсе не имеющие сердечника, или же он является регулируемым, что позволяет менять индуктивность детали.

Намотка проводника может быть как однослойной, ее еще называют рядовой с шагом, или многослойной (применяются названия универсал, внавал, рядовая). Расстояние между витками называется шагом.

Интересно знать! Шаг намотки может быть прогрессивным, то есть его величина изменяется по длине катушки. Применяется такая намотка для снижения «паразитной» емкости.

Применение

Используются катушки в схемах обработки сигналов и аналоговых схемах. В сочетании с конденсаторами и прочими радиокомпонентами могут формировать участки схем, которые усиливают или отфильтровывают определенные сигналы.

Широко применяются дроссели в источниках питания, где они вместе с конденсаторами фильтра призваны устранить остаточные помехи и прочие колебания, возникающие на выходе.

Если две катушки соединить одним магнитным полем, то получится трансформатор – устройство, способное передавать электричество от одной части цепи к другой, за счет электромагнитной индукции, попутно меняя величину напряжения.

Для справки! Трансформаторы способны функционировать только с переменным током.

Основные характеристики катушек индуктивности

Прежде чем разбираться с тем, как ведет себя ток, проходя в цепи через катушку индуктивности, давайте сначала узнаем главные характеристики этого элемента.

• Прежде всего, нас интересует индуктивность – значение, численно выражающаяся соотношением потока магнитного поля, которое создается протекающим током, к силе этого самого тока. Измеряется этот параметр в Генри (Гн).
• Если говорить более простым языком, то это явление можно описать так. При протекании тока через катушку индуктивности создается электромагнитное поле, которое напрямую связано с ЭДС, которая оказывает противодействие изменению переменного напряжения, то есть в цепи возникает ток, который течет в обратном направлении основному.
• Измерение силы тока на катушке индуктивности и переменного напряжения, противостоят данной силе, точнее наоборот. Это свойство элемента называется индуктивным сопротивлением, которое находится в противофазе реактивному емкостному сопротивлению конденсатора, включенному в цепь переменного тока.

Совет! Изменение величины индуктивности катушки происходит пропорционально изменению числа витков.

• Давно известно, что любое магнитное поле обладает некоторой энергией. Отсюда следует, что магнитное поле катушки тоже имеет определенный запас магнитной энергии. Величина этого запаса равна затраченной энергии на обеспечение протекания тока (I) в противодействие ЭДС. Расчеты производятся по приведенной выше формуле.

• Чтобы было еще понятнее давайте сравним катушку с гидротурбиной. Итак, водяной поток, который направлен через турбину, будет ощущать ее сопротивление, пока турбина до конца не раскрутится. Она имеет некоторую инерцию, а значит, будет вращаться синхронно с потоком воды, не оказывая ему практически никакого сопротивления.
• Если вы попробуете остановить поток воды или сменить его направление, то увидите, что турбина продолжит вращаться по инерции, заставляя двигаться воду в прежнем направлении. Чем выше инерция у турбины, тем сильнее она будет сопротивляться изменению направления потока воды.
• Ровно то же самое происходит в катушке индуктивности, когда переменный ток начинает течь в обратном направлении.

• Влияние тока на индуктивность катушки выражается не только в виде основного эффекта взаимодействия. Часто наблюдаются паразитные эффекты, из-за которых сопротивление переменному току катушки индуктивности чисто реактивным назвать нельзя. Из-за этих эффектов в катушке возникают некоторые потери, оценивающиеся как сопротивление потерь. Данное значение составляет сумму потерь в сердечнике, проводе, экране и диэлектрике.
• Каждая из потерь вызвана разными причинами. В проводах их целых три: они обладают хоть и малым, но все же активным омическим сопротивлением; данное сопротивление растет с увеличением частоты, что обусловлено уменьшением амплитуды электромагнитных волн, по мере того как они проникают в глубину проводящей среды (это явление называется скин-эффектом) – другими словами, ток вытесняется на верхние слои провода, из-за чего изменяется площадь проводника, а значит, и его сопротивление; если провода свиты в спираль, возникает эффект близости, из-за которого тоже меняется активное сечение проводника, и общее сопротивление.

• Потери в диэлектрике могут возникать из-за межвиткового конденсатора, или по причине его электромагнитных свойств. Однако справедливости ради стоит отметить, что потери в этой части детали настолько малы, что ими часто пренебрегают при расчетах.
• Потери на сердечнике складываются из двух величин: потери на перемагничивание ферромагнетика (потери на гистерезис) и потери на вихревые токи. Переменное магнитное поле, возникающее от протекающего в проводнике тока, индуцирует вихревые ЭДС в соседних проводниках – сердечнике, проводах ближайших витков, и даже экране. Возникшие токи, имеющие название помимо вихревых, токи Фуко, также являются причиной потерь, из-за активного сопротивления провода.
• С потерями на сопротивление связана и другая характеристика, называемая добротностью. Ее величина – это соотношение реактивного и активного сопротивления катушки индуктивности.

• Следующий параметр – это паразитная емкость. Явление состоит в том, что между витками катушки возникает некоторая нежелательная емкостная связь.
• ТКИ (температурный коэффициент индуктивности) – все мы знаем, что при нагревании вещества увеличиваются в размерах. Когда это происходит с катушкой, мы получаем нестабильность индуктивности, из-за изменения длины и диаметра проводника, длины и диаметра каркаса, а значит, изменения диаметра и шага витков. Помимо этого перемена температуры влияет на диэлектрическую проницаемость материала каркаса, что влечет изменение емкости катушки и влияет на проницаемость магнитным полем ферромагнетика сердечника.
• ТКД (температурный коэффициент дробности) – тут все понятно! Это изменение параметров добротности в зависимости от температуры.

Принцип работы

Чтобы понять принцип действия катушки индукции, следует знать:

• вокруг движущихся электрически заряженных частиц (электрический ток) возникает электромагнитное поле. Если проводник с протекающим током смотан в катушку, поле многократно усиливается. Еще большим оно становится при использовании металлического сердечника, что объясняется высокой магнитопроницаемостью металлов по сравнению с воздухом;
• переменное магнитное поле наводит в проводнике ЭДС (закон электромагнитной индукции, открытый М. Фарадеем).

Способность катушки превращать электрическую энергию в магнитное поле, называется индуктивностью. Она измеряется в генри (Гн), в формулах обозначается литерой L. Катушка индуктивностью в 1 Гн при изменении силы тока со скоростью dI = 1 А/с (ампер в секунду) создает ЭДС в 1 В. Индуктивность катушки зависит от ее длины, потому шаг витков стремятся делать как можно меньшим.

Сердечник в катушке может быть регулируемым, тогда элемент имеет переменную индуктивность. Также применяют катушки вовсе без сердечника. Если катушка включена в цепь постоянного тока, то весь эффект от нее состоит в создании электромагнитного поля. Так устроены, например, электрические магниты для захвата металлолома, устанавливаемые на погрузочных кранах.

При проведении эксперимента надо ограничить ток в цепи, посредством включенной последовательно с катушкой нагрузки, иначе возникнет короткое замыкание.

Включение катушки индуктивности в цепи с постоянным и переменным током

В целом, мы определили, что такое катушка индуктивности, для чего она нужна, и какие характеристики для расчета ее параметров важны, однако до сих пор неискушенному читателю наверняка не понятно, как будут изменяться параметры протекающего через эту деталь тока.

Цепь, питаемая постоянным током

Чтобы упростить изложение, будем проводить очень простой опыт:

• Для начала нам потребуется блок питания, способный выдавать стабильные 12 Вольт напряжения на выходе, 12-ти вольтовая лампочка накаливания для создания сопротивления, а также сама катушка индуктивности.

• Катушку мы соберем своими руками из куска лакированной медной проволоки и ферритового стержня.

• Инструкция предельно проста — берем проволоку и наматываем ее на стержень, после чего зачищаем ножом концы, чтобы можно было подсоединить клеммы от блока питания и подпаять провода.
• Цена такой схемы минимальна, так что можете без проблем повторить опыт при желании дома.

• При помощи LC-метра измеряем индуктивность полученной детали. Как видно из фото выше, в рассматриваемом примере она составила 132 мкГн.

• Теперь берем все наши детали и соединяем их по приведенной выше схеме.

• Вот что получилось на практике. Как видим, постоянный ток протекает через катушку практически беспрепятственно, если не учитывать естественное сопротивление проводника, ведь ток не меняет своего направления на противоположное.

• Значит ли это, что катушка индуктивности неприменима в цепях с постоянным током? Вовсе нет! Вот другая схема, в которую, как мы видим, уже включен некий выключатель, способный размыкать цепь. Именно в момент замыкания и происходит самое интересное.
• Поскольку до этого ток был равен нулю, он начнет изменяться и расти, из-за чего изменится магнитное поле катушки, что в свою очередь приведет к возникновению ЭДС. В катушке появится индукционный ток, который потечет в обратном направлении основного потока от источника питания.
• Именно в момент включения величина ЭДС будет максимальной, так как скорость изменения тока в этот момент наиболее высока, а значит, ток катушки индуктивности равен нулю.
• Что произойдет дальше? А дальше мы увидим, что ток в катушке индуктивности начнет расти, тогда как ЭДС, наоборот, снижаться. Вот как это выглядит на графике.

• На верхнем графике изображено изменение напряжения входной сети, сразу после включения. Как видим, моментально появляется постоянное значение.
• Дальше показано, как меняется величина тока, протекающего через катушку. Он тоже достигает постоянно значения, но не сразу, а спустя какое-то время.
• Напряжение на катушке (нижний график) также вырастает моментально, но тут же начинает падать. При этом обратите внимание, что графики силы тока и напряжения зеркально противоположны.
• Если все это перенести на наш опыт с лампой, то мы увидим, что после соединения цепи через выключатель, она загорится не сразу, а с некоторой задержкой.

Похожая ситуация будет и при размыкании цепи.

По графикам видна противоположная ситуация, означающая, что лампочка продолжить гореть еще какое-то время после размыкания цепи.

Дело в том, что при прекращении подачи питания, в катушке снова возникнет ЭДС, однако ток индукции потечет теперь в том же направлении, что и от источника питания, то есть запасенная энергия в катушке, поддержит питание цепи.

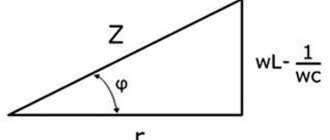
Векторная диаграмма реальной катушки и полное её сопротивление

Несовпадение по фазе слагаемых в выражении (13.12) затрудняет определение амплитуды и действующей величины приложенного к цепи напряжения U. Поэтому воспользуемся векторным способом сложения синусоидальных величин. Амплитуды составляющих общего напряжения

UmR = RIm; UmL = ωLIm ,

а действующие величины

UR = RI; UL = XLI .

Вектор общего напряжения

U = UR + UL

Для того чтобы найти величину вектора U, построим векторную диаграмму (рис. 13.10, а), предварительно выбрав масштабы тока Mi и напряжения Мu.

За исходный вектор диаграммы принимаем вектор тока I. Направление этого вектора совпадает с положительным направлением оси, от которой отсчитываются фазовые углы (начальная фаза заданного тока Ψi =0). Как и ранее, эту ось удобно (но не обязательно) направить по горизонтали.

Вектор UR по направлению совпадает с вектором тока I, а вектор UL направлен перпендикулярно вектору I с положительным углом.

Из диаграммы видно, что вектор тока I общего напряжения U отражает вектор тока I на угол φ>0, но φ<90°, а по величине равен гипотенузе прямоугольного треугольника, катетами которого являются векторы падений напряжения в активном и индуктивном сопротивлениях UR и UL :

UR = Ucosφ

Проекция вектора напряжения U на направление вектора тока называется активной составляющей вектора напряжения и обозначается Ua. Для катушки по схеме рис. 13.9 при Ua = UR

U = Usinφ (13.14)

Проекция вектора напряжения U на направление, перпендикулярное вектору тока, называется реактивной составляющей вектора напряжения и обозначается Up. Для катушки Up = UL

При токе i = Imsinωtуравнение напряжения можно записать на основании векторной диаграммы в виде

U = Umsin(ωt+φ)

Стороны треугольника напряжений, выраженные в единицах напряжения, разделим на ток I. Получим подобный треугольник сопротивлений (рис. 13.10, б), катетами которого являются активное R = UR/I и индуктивное XL = UL/I, сопротивления, а гипотенузой величина Z = U/I.

Отношение действующего напряжения к действующему току данной цепи называется полным сопротивлением цепи. Стороны треугольника сопротивлений нельзя считать векторами, так как сопротивления не являются функциями времени. Из треугольника сопротивлений следует

Понятие о полном сопротивлении цепи Z позволяет выразить связь между действующими величинами напряжения и тока формулой, подобной формуле Ома:

Из треугольников сопротивления и напряжения определяются

cosφ = UR/U = R/Z; sinφ = UL/U = XL/Z; tgφ = UL/UR = XL/R. (13.18)

График зависимости тока и ЭДС самоиндукции от времени

Графически характер изменения тока в цепи и ЭДС самоиндукции с течением времени выглядит так:

Из графика видно, что ЭДС самоиндукции тем больше, чем выше скорость изменения силы тока. В начале периода (участок вблизи т.1 на графике) сила тока возрастает быстро, потому и ЭДС самоиндукции здесь максимальна. К концу первой четверти периода (т. 2) скорость изменения снижается почти до нуля (синусоида принимает горизонтальное положение), после чего сила тока все стремительнее уменьшается (участок между т. 2 и т. 3).

Соответственно, ЭДС самоиндукции снижается в т. 2 до нуля, а затем снова возрастает, но при этом меняет знак на противоположный: теперь она противодействует падению силы тока, то есть ток и ЭДС по знаку совпадают. В следующем полупериоде картина повторяется.

Устройство катушки

Более близким к идеализированному элементу — индуктивности — является реальный элемент электронной цепи — индуктивная катушка. В отличие от индуктивности в индуктивной катушке имеют место также запасание энергии электронного поля и преобразование электронной энергии в другие виды энергии, а именно в термическую. Количественно способность реального и идеализированного частей электронной цепи припасать энергию магнитного поля характеризуется параметром, именуемым индуктивностью.

Таким макаром термин «индуктивность» применяется как заглавие идеализированного элемента электронной цепи, как заглавие параметра, количественно характеризующего характеристики этого элемента, и как заглавие основного параметра индуктивной катушки.

Связь меж напряжением и током в индуктивной катушке определяется законом электрической индукции, из которого следует, что при изменении магнитного потока, пронизывающего индуктивную катушку, в ней наводится электродвижущая сила е, пропорциональная скорости конфигурации потокосцепления катушки ψ и направленная таким макаром, чтоб вызываемый ею ток стремился воспрепятствовать изменению магнитного потока:

e = — dψ / dt

В системе единиц СИ магнитный поток и потокосцепление выражают в веберах (Вб).

Интересно почитать: инструкция как прозвонить транзистор.

Магнитный поток Ф, пронизывающий любой из витков катушки, в общем случае может содержать две составляющие: магнитный поток самоиндукции Фси и магнитный поток наружных полей Фвп: Ф — Фси + Фвп.

1-ая составляющая представляет собой магнитный поток, вызванный протекающим по катушке током, 2-ая — определяется магнитными полями, существование которых не связано с током катушки — магнитным полем Земли, магнитными полями других катушек и неизменных магнитов. Если 2-ая составляющая магнитного потока вызвана магнитным полем другой катушки, то ее именуют магнитным потоком взаимоиндукции.

Потокосцепление катушки ψ, так же как и магнитный поток Ф, может быть представлено в виде суммы 2-ух составляющих: потокосцепления самоиндукции ψси, и потокосцепления наружных полей ψвп

ψ= ψси + ψвп

Наведенная в индуктивной катушке ЭДС е, в свою очередь, может быть представлена в виде суммы ЭДС самоиндукции, которая вызвана конфигурацией магнитного потока самоиндукции, и ЭДС, вызванной конфигурацией магнитного потока наружных по отношению к катушке полей:

e = eси + eвп,

тут еси — ЭДС самоиндукции, евп — ЭДС наружных полей.

Если магнитные потоки наружных по отношению к индуктивной катушке полей равны нулю и катушку пронизывает только поток самоиндукции, то в катушке наводится только ЭДС самоиндукции.

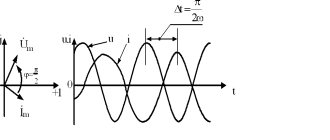
Сдвиг фаз между напряжением и током

Данное явление обусловлено противодействием катушки индуктивности изменению силы тока.

Изучить явление поможет простой опыт, для которого понадобятся следующие устройства и элементы:

• источник постоянного тока;
• осциллограф;
• генератор частоты;
• резистор на 100 Ом;
• катушка индуктивности.

Все элементы последовательно подключаются к источнику постоянного тока. На осциллографе видно две синусоиды, отображающие напряжение на генераторе частоты (красная) и на резисторе (желтая).

Вторую синусоиду можно считать отображением колебаний тока на резисторе, так как он по амплитуде, фазе и частоте всегда соответствует напряжению на данном участке.

Ход опыта:

1. генератор настраивается на частоту в 1 кГц. По осциллографу видно, что фазы обеих синусоид совпадают. Амплитуда на второй синусоиде составляет почти 2 В;
2. увеличивают частоту тока до 100 кГц. Осциллограф отражает два изменения: амплитуда колебаний напряжения на резисторе уменьшилась, а синусоида резистора сдвинулась относительно синусоиды генератора: это и есть сдвиг фаз;
3. при дальнейшем увеличении частоты, наблюдается следующее: амплитуда напряжения на резисторе падает до 480 мВ, а сдвиг фаз увеличивается;
4. при установке максимально возможной частоты, амплитуда напряжения на резисторе падает до 120 мВ. Сдвиг фаз приближается к 900 (четверть периода).

Опыт подтвердил, что индуктивное сопротивление катушки при увеличении частоты возрастает. Попутно наблюдается сдвиг фаз между напряжением источника и током нагрузки, стремящийся к 900.