Лекция по электротехнике по теме «Цепи переменного тока с активным сопротивлением, индуктивностью и емкостью»

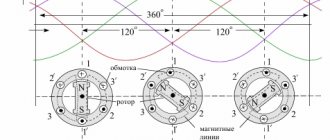
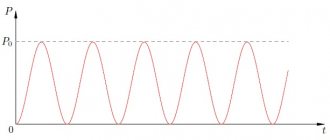
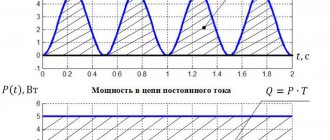
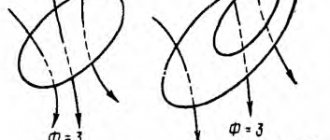Понятие об идеальной емкости

Идеальную емкость в электрических цепях представляет конденсатор. Конденсатор и катушка индуктивности не потребляют мощность, в них \(P=0.\) То есть в данных элементах не осуществляется невозвратная трансформация энергии в иные ее виды, в них циркулирует имеющаяся энергия. Иными словами, электроэнергия запасается в магнитном поле катушки и электрическом поле конденсатора. Этот процесс занимает около четверти периода, после чего она направляется обратно в цепь.

Определение 3

Благодаря происходящим в катушке и конденсаторе процессам, они получили название реактивных элементов. Соответствующим образом и их сопротивления называются реактивными. А вот резистор имеет активное сопротивление.

При обмене энергией интенсивность характеризует максимальное значение скорости притока энергии в магнитное поле катушки и максимальное значение скорости притока энергии в электрическое поле конденсатора. Такая интенсивность является реактивной мощностью и рассчитывается так:

\(Q=UIsinφ\)

При нагрузке на индуктивности \(φ≥0\) реактивная мощность принимает только плюсовые значения. В случае опережающего тока нагрузки емкости – минусовые.

Реактивная мощность идеальной катушки соответствует наибольшему значению запаса энергии в катушке и частоты.

Определение 4

Коэффициентом мощности является соотношение полной и активной мощности. Его значение определяют как косинус угла смещения между током и напряжением

Наряду с полной и активной мощностью существует понятие комплексной мощности. Реактивная мощность является характеристикой циркуляции энергии между источником и приемником. Реактивный ток не производит никакой работы и это влечет за собой потери на силовых установках, а соответственно повышение мощности. Потому на сегодняшний день есть тенденция к увеличению мощности электрических сетей.

Некоторые приемники электроэнергии, например, двигатели, пользуются активно-индуктивной нагрузкой. Если к данной нагрузке подключить конденсатор, то общий ток приемника будет достигать величины фазы напряжения. То есть, он будет расти, но его общее значение будет падать при постоянной активной мощности. Все это влечет потери общего тока цепи. Конденсаторы применяют для повышения мощности.

Сложно разобраться самому?

Попробуй обратиться за помощью к преподавателям

Решение задач Контрольные работы Эссе

Мгновенная мощность

Для мгновенного определения мощности в электрической цепи вводится формула в виде:

Ты эксперт в этой предметной области? Предлагаем стать автором Справочника Условия работы

$p = ui$

Мгновенная мощность обладает двумя видами элементов:

• постоянной составляющей;
• гармонической составляющей.

Мгновенная мощность имеет угловую частоту, которая превышает угловую частоту напряжения и тока в два раза. При отрицательных значениях мгновенной мощности энергия будет возвращаться к источнику питания. Это говорит о том, что направления напряжения и тока имеют противоположные значения в двухполюснике.

Подобное возвращение энергии к источнику происходит из-за того, что идет энергетический запас в электрических и магнитных полях на уровне емкостных и индуктивных элементов. Они входят в состав двухполюсника.

Определение 2

Активная мощность – среднее значение мгновенной мощности за определенный период времени.

$P = UI cos \phi$

Активная мощность при потреблении пассивным двухполюсником не имеет отрицательных значений. На входе пассивного двухполюсника будет фиксироваться $cos \phi \geq 0$. Ситуация, при которой $P=0$, возможна в теории, но только для двухполюсника без активных сопротивлений. В нем должны быть:

Готовые работы на аналогичную тему

Курсовая работа Емкость и мощность электрической цепи 490 ₽ Реферат Емкость и мощность электрической цепи 260 ₽ Контрольная работа Емкость и мощность электрической цепи 240 ₽

Получить выполненную работу или консультацию специалиста по вашему учебному проекту Узнать стоимость

• емкостные элементы;
• идеальные индуктивные элементы.

Рис.1.48

[/td]
где — амплитуда тока,

— начальная фаза.

Сдвиг фаз между напряжением и током в цепи с емкостью равен т.е. ток в цепи с емкостью опережает по фазе приложенное напряжение на 90° (рис.1.49).

Комплексное сопротивление цепи с емкостью

§53. Емкость в цепи переменного тока

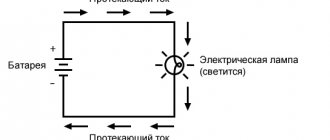
Ток и напряжение. В цепи постоянного тока емкость (идеальный конденсатор) имеет сопротивление бесконечно большое, так как после окончания процесса заряда такой конденсатор не пропускает электрический ток. Однако при подключении емкости к источнику переменного тока (рис. 191,а) происходит непрерывный процесс его заряда и разряда, при этом через емкость проходит переменный ток.

Ток i при включении в цепь переменного тока емкости определяется количеством электричества q, проходящим по этой цепи в единицу времени. Следовательно,

i = ?q / ?t

где ?q — изменение количества электричества (заряда q) за время ?t.

Количество электричества q, накопленное в конденсаторе при изменении напряжения и, также непрерывно изменяется. Поэтому, учитывая формулу (69), будем иметь:

i = C ?u / ?t

где ?u — изменение напряжения и за время ?t.

Из рис. 191,б видно, что скорость изменения напряжения ?u/?t будет наибольшей в моменты времени, когда угол ?t равен 0; 180 и 360°. Следовательно, в эти моменты времени ток i имеет максимальное значение. В моменты же времени, когда угол ?t равен 90° и 270°, скорость изменения напряжения ?u/?t = 0 и поэтому i = 0.

В течение первой четверти периода происходит заряд емкости и в цепи течет ток заряда, который считаем положительным. При этом по мере заряда емкости и увеличения разности потенциалов на электродах ток i уменьшается. При ?t = 90° емкость полностью заряжается, разность потенциалов на электродах становится равной напряжению и источника и ток i = 0.

Во второй четверти периода емкость начнет разряжаться и ток i изменяет свое направление (становится отрицательным). При

?t =180°, когда u = 0, ток i разряда достигает максимального значения. В этот момент изменяется полярность напряжения и источника и начинается процесс перезаряда емкости при противоположном (отрицательном) направлении тока i. При со/ = 270° заряд прекращается, ток i становится равным нулю и начинается разряд при первоначальном (положительном) направлении тока.

Таким образом, емкость в течение одного периода изменения напряжения и дважды заряжается и дважды разряжается. Следовательно, в цепи (см. рис. 191, а) непрерывно протекает переменный ток i. Из рис. 191,б видно, что при включении в цепь переменного тока емкости ток i опережает по фазе напряжение и на угол 90° или же что напряжение и отстает по фазе от тока i на угол 90° (рис. 191,в).

Емкостное сопротивление. Сопротивление, которое оказывает емкость переменному току, называют емкостным. Оно обозначается Xс и измеряется в омах. Физически емкостное сопротивление обусловлено действием э. д. с. ес, возникающей в конденсаторе С. Эта э. д. с. направлена против приложенного напряжения u, так как заряженный конденсатор можно рассматривать как источник с некоторой э. д. с. ес, действующей между его пластинами. Поэтому э. д. с. ес препятствует изменению тока под действием напряжения u, т. е. оказывает прохождению переменного тока определенное сопротивление.

Из формулы (70) следует, что чем больше емкость С и скорость изменения напряжения ?u/?t, т. е. частота его изменения f (значение ?), тем больше ток i в цепи с емкостью и тем меньше емкостное сопротивление:

Xс = 1 /(?C)

Закон Ома для цепи с емкостью:

I = U / Xс = U / ( 1 /(?C) )

Электрическая мощность. Рассмотрим, как изменяется электрическая мощность в цепи переменного тока с емкостью. Ее можно получить графическим путем, перемножая ординаты кривых тока и напряжения при различных углах ?t. Кривая мгновенной мощности (см. рис. 179,б) представляет собой синусоиду, которая изменяется с двойной частотой 2? по сравнению с частотой изменения тока i и напряжения u. Следовательно, в этой цепи тоже имеет место непрерывный колебательный процесс обмена энергией между источником и емкостью. В первую и третью четверти периода мощность положительна, т. е. конденсатор получает энергию W от источника и накапливает ее в своем электрическом поле. Во вторую и четвертую четверть периода конденсатор отдает накопленную энергию источнику (мощность отрицательна); при этом протекание тока по цепи поддерживается э. д. с. ес. В целом за период в емкостное сопротивление не поступает электрическая энергия (среднее значение мощности за период равно нулю). Поэтому емкостное сопротивление, так же как и индуктивное, относят к группе реактивных сопротивлений.

Для характеристики процесса обмена энергией между источником и емкостью введено понятие реактивной мощности емкости:

Qс = UсI

где Uс — напряжение, приложенное к конденсатору (действующее значение) .

Эту мощность можно выразить также в виде

Qс = U2с/ Xс или Qс = I2Xс

Следует отметить, что в реальных конденсаторах имеют место потери мощности, вследствие чего они потребляют от источника некоторую электрическую энергию. Потери мощности вызваны тем, что в диэлектрике, разделяющем пластины конденсатора, под действием переменного электрического поля возникают токи смещения, нагревающие диэлектрик. Чем больше напряжение и частота его изменения, тем больше потери мощности в конденсаторах от токов смещения. Однако эти потери имеют значение только в конденсаторах, применяемых в высокочастотных установках. При стандартной частоте 50 Гц потери в конденсаторах настолько малы, что их обычно не учитывают.

ИНФОФИЗ

Рассмотрим по отдельности случаи подключения внешнего источника переменного тока к резистру с сопротивлением R

, конденсатору емкости
C
и катушки индуктивности
L
. Во всех трех случаях напряжения на резисторе, конденсаторе и катушке равны напряжению источника переменного тока.

1. Резистор в цепи переменного тока

Сопротивление R называют активным, потому что цепь с таким сопротивлением поглощает энергию.

Активное сопротивление — устройство, в котором энергия электрического тока необратимо преобразуется в другие виды энергии (внутреннюю, механическую)

Пусть напряжение в цепи меняется по закону: u = Umcos ωt ,

тогда сила тока меняется по закону: i = u/R = IRcosωt

u – мгновенное значение напряжения;

i – мгновенное значение силы тока;

IR

— амплитуда тока, протекающего через резистор.

Связь между амплитудами тока и напряжения на резисторе выражается соотношением RIR

=
UR
Колебания силы тока совпадают по фазе с колебаниями напряжения. (т.е. фазовый сдвиг между током и напряжением на резисторе равен нулю).

2. Конденсатор в цепи переменного тока

При включении конденсатора в цепь постоянного напряжения сила тока равна нулю, а при включении конденсатора в цепь переменного напряжения сила тока не равна нулю. Следовательно, конденсатор в цепи переменного напряжения создает сопротивление меньше, чем в цепи постоянного тока.

Соотношение между амплитудами тока IC

и напряжения

UC

:

Ток опережает по фазе напряжение на угол π/2.

3. Катушка в цепи переменного тока

В катушке, включенной в цепь переменного напряжения, сила тока меньше силы тока в цепи постоянного напряжения для той же катушки. Следовательно, катушка в цепи переменного напряжения создает большее сопротивление, чем в цепи постоянного напряжения.

Соотношение между амплитудами тока IL

и напряжения
UL
:

ωLIL

=
UL
Ток отстает по фазе от напряжения на угол π/2.

Теперь можно построить векторную диаграмму для последовательного RLC-контура, в котором происходят вынужденные колебания на частоте ω. Поскольку ток, протекающий через последовательно соединенные участки цепи, один и тот же, векторную диаграмму удобно строить относительно вектора, изображающего колебания тока в цепи. Амплитуду тока обозначим через I

0. Фаза тока принимается равной нулю. Это вполне допустимо, так как физический интерес представляют не абсолютные значения фаз, а относительные фазовые сдвиги.

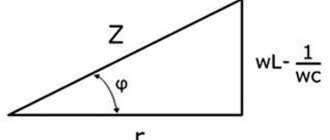
Векторная диаграмма на рисунке построена для случая, когда или В этом случае напряжение внешнего источника опережает по фазе ток, текущий в цепи, на некоторый угол φ.

Векторная диаграмма для последовательной RLC-цепи

Из рисунка видно, что

откуда следует

Из выражения для I

0 видно, что амплитуда тока принимает максимальное значение при условии

или

Явление возрастания амплитуды колебаний тока при совпадении частоты ω внешнего источника с собственной частотой ω0 электрической цепи называется электрическим резонансом

. При резонансе

Сдвиг фаз φ между приложенным напряжением и током в цепи при резонансе обращается в нуль. Резонанс в последовательной RLC-цепи называется резонансом напряжений

. Аналогичным образом с помощью векторной диаграммы можно исследовать явление резонанса при параллельном соединении элементов
R
,
L
и
C
(так называемый
резонанс токов
).

При последовательном резонансе (ω = ω0) амплитуды UC

и
UL
напряжений на конденсаторе и катушке резко возрастают:

Рисунок иллюстрирует явление резонанса в последовательном электрическом контуре. На рисунке графически изображена зависимость отношения амплитуды UC

напряжения на конденсаторе к амплитуде 0 напряжения источника от его частоты ω. Кривые на рисунке называются
резонансными кривыми
.