Трансформатор, как элемент радиотехники и электротехники, работает на основе электромагнитной индукции. Говоря об индуктивности трансформатора, имеют в виду индуктивность обмоток и взаимоиндукцию между ними.
Каждая из обмоток представляет некоторое количество витков провода, намотанных на ферромагнитный сердечник, то есть обыкновенную катушку индуктивности.
Трудность в определении параметров катушки заключается в том, что они изменяются в зависимости от нескольких параметров и их сочетания:
- токи в обмотках;
- уровень намагниченности магнитопровода;
- магнитные характеристики сердечника;
- взаимодействие между соседними обмотками;
- наличия постоянной составляющей тока.
Конструкция и принцип действия силового трансформатора
В основе конструкции любого трансформатора находятся следующие элементы:
- Сердечник из ферромагнитного материала.
- Первичная и вторичные обмотки. В случае автотрансформатора одна обмотка выполняет обе функции.
В сетях переменного тока промышленной частоты (50 или 60Гц) в качестве ферромагнитного материала используется сталь, обработанная по специальной технологии. На высоких частотах часто делаются трансформаторы без сердечника, поскольку для нормальной работы достаточно взаимосвязи межу катушками.
Принцип работы:
- в первичной обмотке, подключенной в цепь питания, создается переменное электрическое поле;
- под действием поля первичной катушки в сердечнике создается переменное магнитное поле;
- в силу электромагнитной индукции во всех обмотках наблюдается ЭДС индукции.
ЭДС индукции в первичной обмотке направлена противоположно поданному напряжению, поэтому они взаимно компенсируются. В результате, при отсутствии нагрузки через первичную обмотку протекает сравнительно небольшой ток холостого хода.
Наличие тока вторичной цепи аналогично вызывает дополнительный магнитный поток, а он – ЭДС самоиндукции в первичное катушке. В результате компенсация первичного напряжения снижается и растет ток в первичной цепи.
Расчет импульсного трансформатора для двухтактного преобразователя и согласующих устройств
В правильно сконструированном двухтактном преобразователе постоянный ток через обмотку и подмагничивание сердечника отсутствуют. Это позволяет использовать полный цикл перемагничивания и получить максимальную мощность. Поскольку трансформатор имеет много взаимозависимых параметров, расчет ведут по шагам, уточняя при необходимости исходные данные.
Как определить число витков и мощность?
Габаритная мощность, полученная из условия не перегрева обмотки, равна [1]:
Pгаб = So ⋅ Sc ⋅ f ⋅ Bm / 150 (1)
Где: Pгаб — мощность, Вт; Sc — площадь поперечного сечения магнитопровода, см2 ; So — площадь окна сердечника, см2; f — частота колебаний, Гц; Bm = 0,25 Тл — допустимое значение индукции для отечественных никель-марганцевых ферритов на частотах до 100 кГц.
Максимальную мощность трансформатора выбираем 80% от габаритной:
Pmax = 0,8 ⋅ Pгаб (2)
Минимальное число витков первичной обмотки n1 определяется максимальным напряжением на обмотке Um и допустимой индукцией сердечника Bm:
n1 = ( 0,25 ⋅ 104 ⋅ Um ) / ( f ⋅ Bm ⋅ Sc ) (3)
Размерности единиц здесь те же, что и в формуле (1).
Плотность тока в обмотке j для трансформаторов мощностью до 300 Вт принимаем 3..5 А/мм2 (большей мощности соответствует меньшее значение). Диаметр провода в мм рассчитываем по формуле:
d = 1,13 ⋅ ( I / j )1/2 (4)
Где I — эффективный ток обмотки в А.
Пример 1:
Для ультразвуковой установки нужен повышающий трансформатор мощностью 30..40 Вт. Напряжение на первичной обмотке синусоидальное, с эффективным значением Uэфф = 100 В и частотой 30 кГц.
Выберем ферритовое кольцо К28x16x9.
Площадь его сечения: Sc = ( D — d ) ⋅ h / 2 = ( 2,8 — 1,6 ) ⋅ 0,9 / 2 = 0,54 см2Площадь окна: So = π ⋅ ( d / 2 )2 = π⋅ ( 1,6 / 2 )2 = 2 см2Габаритная мощность: Pгаб = 0,54 ⋅ 2 ⋅ 30 ⋅ 103 ⋅ 0,25 / 150 = 54 ВтМаксимальная мощность: Pmax = 0,8 ⋅ 54 = 43,2 ВтМаксимальное напряжение на обмотке: Um = 1,41 ⋅ 100 = 141 ВЧисло витков: n1 = 0,25 ⋅104 ⋅ 141 / ( 30 ⋅ 103 ⋅ 0,25 ⋅ 0,54 ) = 87Число витков на вольт: n0 = 87 / 100 = 0,87Эффективное значение тока первичной обмотки: I = P / U = 40 / 100 = 0,4 AПлотность тока выберем 5 А/мм2. Тогда диаметр провода по меди: d = 1,13 ⋅ ( 0,4 / 5 )1/2 = 0,31 мм
Как уточнить плотность тока?
Если мы делаем маломощный трансформатор, то можем поиграть с плотностью тока и выбрать более тонкие провода, не опасаясь их перегрева. В книге Эраносяна [2, Стр.109] дана такая табличка:
| Pн, Вт | 1 .. 7 | 8 .. 15 | 16 .. 40 | 41 .. 100 | 101 .. 200 |
| j, А/мм2 | 7 .. 12 | 6 .. 8 | 5 .. 6 | 4 .. 5 | 4 .. 4,5 |
Почему плотность тока зависит от мощности трансформатора?
Выделяемое количество теплоты равно произведению удельных потерь на объем провода. Рассеиваемое количество теплоты пропорционально площади обмотки и перепаду температур между ней и средой. С увеличением размера трансформатора объем растет быстрее площади и для одинакового перегрева удельные потери и плотность тока надо уменьшать. Для трансформаторов мощностью 4..5 кВА плотность тока не превышает 1..2 А/мм2 [3].
3. Как уточнить число витков первичной обмотки?
Зная число витков первичной обмотки n вычислим ее индуктивность. Для тороида она определяется по формуле:
L = μ0 ⋅ μ ⋅ Sс ⋅ n2 / la (5)
Где: Площадь Sс дана в м2; средняя длина магнитной линии la в м; индуктивность в Гн; μ0 = 4π ⋅ 10-7 Гн/м — магнитная постоянная.
В инженерном виде эта формула выглядит так:
L = AL n2 (5А) , n = ( L / AL )1/2 (5Б)
Коэффициент AL и параметр мощности Sо ⋅ Sc для некоторых типов колец приведены в Таблице 2 [4,5,6]:
| Кольцо | К7х4х2 | К10х6х3 | К10х6х4,5 | К16х10х4,5 | К20х12х6 | К32х20х6 | К38х24х7 | К40х25х11 |
| AL , нГн/вит2 ± 25% | 224 | 310 | 460 | 430 | 620 | 570 | 650 | 1050 |
| Sо ⋅ Sc , см4 | 0,004 | 0,017 | 0,025 | 0,106 | 0,271 | 1,131 | 2,217 | 4,050 |
Для работы трансформатора в качестве согласующего устройства должно выполняться условие:
L > ( 4 .. 10 ) ⋅ R / ( 2 ⋅ π ⋅ fmin ) (6)
Где L — индуктивность в Гн; R = U2эфф / Pн приведенное к первичной обмотке сопротивление нагрузки Ом; fmin — минимальная частота, Гц.
В ключевых преобразователях в первичной обмотке трансформатора текут два тока: прямоугольный ток нагрузки Iпр = Um / R и треугольный ток намагничивания обмотки IT:
Для нормальной работы преобразователя величина треугольной составляющей не должна превышать 10% от прямоугольной, т.е индуктивность обмотки должна удовлетворять неравенству:
L > 5 R / f (7)
При необходимости число витков увеличивают или применяют феррит с большей μ. Чрезмерно завышать число витков в обмотке не желательно. Из-за роста межвитковой емкости на рабочей частоте могут возникнуть резонансные колебания.
Выбранный феррит должен иметь достаточную максимальную индукцию и малые потери в рабочей полосе частот. Как правило, на низких частотах (до 1 МГц) применяют феррит с μ = 1000 .. 6000 , а на радиочастотах приходиться использовать материалы с μ = 50 .. 400.
Пример 2:
Трансформатор из Примера 1 намотан на кольце К28х16х9 из никель-марганцевого феррита 2000НМ с магнитной проницаемостью μ = 2000. Мощность нагрузки P = 40 Вт , эффективное напряжение первичной обмотки Uэфф = 100 В , частота f = 30 кГц. Уточним число его витков.
Приведенное сопротивление нагрузки: R = 1002 / 40 = 250 ОмПлощадь поперечного сечения магнитопровода: Sc = 0,54 см2 = 0,54 ⋅ 10 -4 м2Средняя длина магнитной линии: la = π ( D +d ) / 2 = π ( 2,8 + 1,6 ) ⋅ 10 -2 / 2 = 6,9 ⋅ 10 -2 м Коэффициент индуктивности: AL = 4π ⋅ 10-7 ⋅ 2000 ⋅ 0,54 ⋅ 10 -4 / 6,9⋅10-2 = 1966 нГн / вит2
Минимальная индуктивность первичной обмотки по формуле (6): L = 10 ⋅ 250 / ( 2π ⋅ 3 ⋅ 104 ) = 13,3 мГнЧисло витков: n = (13,3 ⋅ 10 -3 / 1,963 ⋅ 10 -6 ) 1/2 = 82
Оно даже меньше, чем рассчитанное ранее в Примере 1 nmin = 87. Таким образом, условие достаточной индуктивности выполнено и число витков первичной обмотки n = 87.
Какие ферриты можно применить и почему?
Как известно, сердечник в трансформаторе выполняет функции концентратора электромагнитной энергии. Чем выше допустимая индукция B и магнитная проницаемость μ , тем больше плотность передаваемой энергии и компактнее трансформатор. Наибольшей магнитной проницаемостью обладают т.н. ферромагнетики — различные соединения железа, никеля и некоторых других металлов.
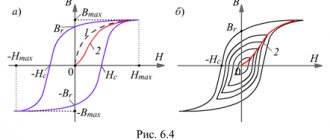
Магнитное поле описывают две величины: напряженность Н (пропорциональна току обмотки) и магнитная индукция В (характеризует силовое действие поля в материале). Связь В и H называют кривой намагничивания вещества. У ферромагнетиков она имеет интересную особенность — гистерезис (греч. отстающий) — когда мгновенный отклик на воздействие зависит от его предыстории.
После выхода из нулевой точки (этот участок называют основной кривой намагничивания) поля начинают бегать по некой замкнутой кривой (называемой петлей гистерезиса). На кривой отмечают характерные точки — индукцию насыщения Bs, остаточную индукцию Br и коэрцитивную силу Нс.
Рис.1. Магнитные свойства ферритов. Слева форма петли гистерезиса и ее параметры. Справа основная кривая намагничивания феррита 1500НМ3 при различных температурах и частотах: 1 — 20кГц, 2 — 50кГц, 3 — 100 кГц.
По значениям этих величин ферромагнетики условно делят на жесткие и мягкие. Первые имеют широкую, почти прямоугольную петлю гистерезиса и хороши для постоянных магнитов. А материалы с узкой петлей используют в трансформаторах. Дело в том, что в сердечнике трансформатора есть два вида потерь — электрические, и магнитные. Электрические (на возбуждение вихревых токов Фуко) пропорциональны проводимости материала и частоте, а вот магнитные тем меньше, чем меньше площадь петли гистерезиса.
Ферриты это пресс порошки окисей железа или других ферромагнетиков спеченные с керамическим связующим. Такая смесь сочетает два противоположных свойства — высокую магнитную проницаемость железа и плохую проводимость окислов. Это минимизирует как электрические, так и магнитные потери и позволяет делать трансформаторы, работающие на высоких частотах. Частотные свойства ферритов характеризует критическая частота fc , при которой тангенс потерь достигает 0,1. Тепловые — температура Кюри Тс , при которой μ скачком уменьшается до 1.
Отечественные ферриты маркируются цифрами, указывающими начальную магнитную проницаемость, и буквами, обозначающими диапазон частот и вид материала.
Наиболее распространен низкочастотный никель-цинковый феррит, обозначаемый буквами НН. Имеет низкую проводимость и сравнительно высокую частоту fc. Но у него большие магнитные потери и невысокая температура Кюри.
Никель-марганцевый феррит имеет обозначение НМ. Проводимость его больше, поэтому fc низкая. Зато малы магнитные потери, температура Кюри выше, он меньше боится механических ударов.
Иногда в маркировке ферритов ставят дополнительную цифру 1, 2 или 3. Обычно, чем она выше, тем более температурно стабилен феррит.
Какие марки ферритов нам наиболее интересны?
Для преобразовательной техники хорош термостабильный феррит 1500НМ3 с fc=1,5 МГц, Bs=0,35..0,4 Тл и Tc=200 ℃.
Для спец применений выпускают феррит 2000НМ3 с нормируемой дезакаммодацией (временной стабильностью магнитной проницаемости). У него fc=0,5 МГц, Bs=0,35..0,4 Тл и Tc=200 ℃.
Для мощных и компактных трансформаторов разработаны ферриты серии НМС. Например 2500НМС1 с Bs=0,45 Тл и 2500НМС2 c Bs=0,47 Тл. Их критическая частота fc=0,4 МГц, а температура Кюри Tc>200 ℃.
Что касается допустимой индукции Bm, этот параметр подгоночный и в литературе не нормируется. Ориентировочно можно считать Bm = 0,75 Вsmin. Для никель-марганцевых ферритов это дает примерно 0,25 Тл. С учетом падения Bs при повышенных температурах и за счет старения в ответственных случаях лучше подстраховаться и снизить Bm до 0,2 Тл.
Основные параметры распространенных ферритов сведены в Таблицу 3:
| Марка | 100НН | 400НН | 600НН | 1000 НН | 2000 НН | 2000 НМ | 1000 НМ3 | 1500 НМ1 | 1500 НМ3 |
| μнач | 80..120 | 350.. 500 | 500.. 800 | 800.. 1200 | 1800.. 2400 | 1700.. 2500 | 800.. 1200 | 1200.. 1800 | 1200.. 1800 |
| fc, МГц | 7 | 3,5 | 1,5 | 0,4 | 0,1 | 0,5 | 1,8 | 0,7 | 1,5 |
| Tc, ℃ | 120 | 110 | 110 | 110 | 70 | 200 | 200 | 200 | 200 |
| Bs, Тл | 0,44 | 0,25 | 0,31 | 0,27 | 0,25 | 0,38.. 0,4 | 0,33 | 0,35.. 0,4 | 0,35.. 0,4 |
Насколько нагреется сердечник?
Потери в магнетике.
При частоте менее критической fс потери энергии в магнетике складываются в основном из потерь на перемагничивание, а вихретоковыми можно пренебречь.
Опыт и теория показывают, что потери энергии в единице объема (или массы) на одном цикле перемагничивания прямо пропорциональны площади петли гистерезиса. Следовательно мощность магнитных потерь:
PH = P0 ⋅ V ⋅ f (8)
Где: P0 – удельные потери в единице объема (измеренные на частоте f0 при индукции B0 ) ; V – объем образца.
Таблица 4. Удельные объемные потери в ферритах 2500НМС при f0 =16 кГц ; B0=0,2 Тл:
| T , oC | P0 , мкВт / ( см 3 ⋅ Гц ) | |
| 2500НМС1 | 2500НМС2 | |
| 25 | 10,5 | 8,5 |
| 100 | 8,7 | 6 |
Однако, с ростом частоты индукция насыщения уменьшается, петля гистерезиса деформируется, а потери растут. Для учета этих факторов Штейнмец (C. P. Steinmetz, 1890-1892) предложил эмпирическую формулу:
PH = P1 ⋅ m ⋅ ( f / f1 ) α ( B / B1) β (9)
Условились [7, Стр.54], что f1 = 1 кГц, B1 = 1 Тл. Величины P1, α, β и массу сердечника m указывают в справочнике.
Таблица 5. Удельные потери в некоторых ферритах
| Марка | 1500НМ3 | 2000НМ1-А,Б | 2000НМ3 | 2000НМ-17 | 3000 НМ-А | 6000НМ-1 | |||
| f | — | 0,4..100 кГц | 0,1..1 МГц | — | 0,4..100 кГц | 0,1..1 МГц | 0,4..200 кГц | 20..50 кГц | 50..100 кГц |
| P1, Вт / кг | 23,2 | 32±7 | 13±3 | 44,6 | 63±10 | 25±4 | 48±8 | 11±2 | 38±0,8 |
| α | 1,2 | 1,2 | 1,4 | 1,3 | 1,2 | 1,4 | 1,2 | 1,35 | 1,6 |
| β | 2,2 | 2,4 | 2,7 | 2,85 | 2,76 | 2,69 | 2,6 | ||
Потери в меди.
Омические потери в первичной обмотке при комнатной температуре и без учета скин-эффекта:
PM1 = I2 эфф ( ρ / Sm ) ( ( D — d ) + 2h ) ⋅ n1 (10)
Где: Iэфф — эффективный ток, D — внешний, d — внутренний диаметр кольца, h — его высота в метрах; n1 — число витков; Sm — поперечное сечение провода, в мм2 ; ρ = 0,018 Ом ⋅ мм2 / м — удельное сопротивление меди.
Суммарные потери во всех обмотках при повышенной температуре окружающей среды:
PM = ( PM1 + PM2 + .. )⋅ ( 1 + 0,004⋅ ( T — 25oC ) ) (11)
Общие потери в трансформаторе.
Потери в магнетике и меди:
PΣ = PH + PM (12)
Предполагаемая температура перегрева при естественной конвекции:
ΔT = PΣ / ( αm Sохл ) (13)
Где αm = (10..15) -4 Вт/(см2oС) , Sохл = π /2 ( D2 — d2 ) + π h ( D + d )
Пример 3:
Найдем потери в трансформаторе из Примеров 1 и 2. Для простоты считаем, что вторичная и первичная обмотка одинаковые.
Эффективный ток первичной обмотки Iэфф = 0,4 А.
Потери в меди первичной обмотки: PM1 = 0,42 ⋅ ( 0,018 / 0,08 ) ⋅ ( 28 — 16 + 18 ) ⋅ 10 -3 ⋅ 87 ≈ 0,1 Вт.
Потери в меди обеих обмоток: PM = 0,2 Вт.
Согласно справочным данным для феррита 2000НМ P1 = 32 Вт / кг ; α = 1,2 ; β = 2,4 ; масса сердечника К28х16х9 равна 20 грамм.
Потери в феррите: PH = 32 ⋅ ( 30 / 1 ) ⋅ 1,2 ⋅ ( 0,25 / 1 ) ⋅ 2,4 ⋅ 20 ⋅ 10 -3= 1,36 Вт
Суммарные потери в трансформаторе: PΣ = 1,56 Вт.
Ориентировочный КПД = ( 40 — 1,56 ) / 40 ⋅ 100% ≈ 96%
Как учесть инерционные свойства трансформатора?
На Рис.2. показана T-схема замещения трансформатора. В нее входят сопротивление источника ri , приведенное сопротивление нагрузки R = n2 Rн или R = Pн / U2эфф , где n = U1 / U2 — коэффициент трансформации, Uэфф — эффективное напряжение первичной обмотки.
Рис.2. Эквивалентная схема трансформатора.
Инерционные свойства трансформатора определяют малые индуктивности рассеяния Ls, индуктивность намагничивания Lμ (почти равна индуктивности первичной обмотки L1), параллельная емкость обмотки Сp (т.н. динамическая емкость) и последовательная емкость между обмотками Сп.
Как оценить индуктивности и емкости?
L1 рассчитывают по формуле (5) или измеряют экспериментально. Согласно [8] индуктивность рассеивания по порядку величины равна Ls ~ L1 / μ. Емкость Ср составляет примерно 1 пФ на виток.
Трансформатор работает подобно полосовому фильтру. На малых частотах он представляет собой ФВЧ с частотой среза ωн = R / Lμ. На высоких частотах элементы Ls и Cp образуют ФНЧ с частотой среза ωв ≈ ( Ls Cp )-1/2Последовательная емкость Сп невелика и на работу практически не влияет.
В модели есть два характерных резонанса:
Низкочастотный (резонанс намагничивания) в параллельном контуре Lμ Ср.Его частота fμ ≈ ( 1/ 2 π ) ⋅ (Lμ Cp )-1/2 , а добротность Qμ ≈ ( ri || R ) ⋅ ( Lμ / Cp)-1/2 (14)
Высокочастотный (резонанс рассеивания) в контуре, образованном Ls и Cр. Его частота fs ≈ ( 1/ 2 π ) ⋅ (Ls Cp )-1/2 , а добротность Qs ≈ ( Ls / Cp)1/2 / ri (15)
Как влияют резонансы обмотки?
Амплитудно-частотная характеристика трансформатора похожа на АЧХ полосового фильтра, но на ее верхнем краю резонанс fs дает характерный пик.
Реакция же на импульсы напряжения зависит от способа включения источника и величин сопротивлений схемы.
При малом внутреннем сопротивлении источника riпроявляется лишь резонанс fs в виде характерного «звона» на фронтах импульсов. Если же источник подключается через ключ, то при его размыкании могут возникать интенсивные колебания с частотой fμ.
Рис.3. Пример АЧХ и переходного процесса в трансформаторе. Его эквивалентная схема дана ниже на рисунке 4.
Экспериментальное измерение параметров импульсного трансформатора.
Для пробы было взято кольцо из феррита 3000НМ размера К10х6х2. Первичная обмотка составляла 21 виток; вторичная 14; коэффициент трансформации n = 1,5 ; сопротивление нагрузки равнялось 4,7 кОм; источником служил генератор прямоугольных импульсов на TTL микросхемах с уровнем 6В, частотой 1 МГц и внутренним сопротивлением ri ≈ 200 Ом.
Рассчитаем теоретические параметры:
Sc = 4 ⋅ 10 -6 м2 , la = 25,13 ⋅ 10 -3 м , ALтеор = 600 нГн / вит2 , L1теор = 0,6 ⋅ 212 = 265 мкГн, Ls теор ≈ 265/3000 = 0,09 мкГн , Сp теор ≈ 21+14 = 35 пФ. Приведенное сопротивление нагрузки R = n2 Rн = 2,25 ⋅ 4,7 ~ 10 кОм.
Результаты измерений индуктивностей прибором АКИП-6107:
L1 = 269 мкГн , L2 = 118 мкГн , закоротив вторичную обмотку получим 2Ls = 6,8 мкГн, что на два порядка выше ее теор оценки.
Динамическую емкость Cp можно оценить по формуле (15), подав на трансформатор прямоугольные импульсы и измерив при помощи осциллографа период колебаний «звона» на фронтах импульсов на выходе вторичной обмотки. Частота «звона» fs оказалась 18,5 МГц , что дает Ср ≈ 21 пФ и неплохо согласуется с теор оценкой.
Для сравнения с опытом эквивалентная схема с измеренными параметрами моделировалась в программе LT Spice.
Рис.4. Модель трансформатора. Vout — приведенное напряжение, фактическое будет в n раз меньше.
Рис.5. Результаты эксперимента. Масштаб вертикальной шкалы 1 вольт на деление.
Итак, модель, построенная на основе измеренных Lμ , Ls и Cp вполне согласуется с экспериментом.
Теоретическая оценка [8] емкости 1 пФ на виток для малых колец приемлема, но оценка индуктивности рассеяния на два порядка расходится с фактической. Ее проще определять на опыте.
Приложение 1. Вывод формулы для числа витков.
При подаче напряжения U на обмотку в ней возникнет ЭДС индукции E: U = -E = n Sc dB / dt
Для синусоидального напряжения с амплитудой Um: Um = n Sc ω BmОткуда число витков: n = Um / ( Sc ω Bm )
Выразив круговую частоту через обычную, а площадь в см2 получим инженерную формулу:
n = 0,16 ⋅ 104 / ( f ⋅ Bm⋅ Sc )
Для прямоугольного напряжения величиной Um приращение индукции: dB = dt Um / ( n Sc )Интегрируя ее по времени от 0 до T/2 и учитывая, что за половину периода поле изменится от -Bm до +Bm получим: 2Bm = ( T / 2) Um / ( n Sc )
Выразив период через частоту, а площадь в см2 получим инженерную формулу:
n = 0,25 ⋅104 / ( f ⋅ Bm ⋅ Sc )
Она пригодна для обоих случаев.
Приложение 2. Вывод формулы для габаритной мощности трансформатора.
Согласно закону электромагнитной индукции Фарадея связь напряжения на катушке с изменением магнитной индукции в ней:
U dt = n Sc dB
За время от 0 до T/2 индукция изменится от -Bm до +Bm. Интегрируя в этих пределах получим среднее напряжение:
Uср = 4n ⋅ Sc ⋅ Bm ⋅ f
Где:
Но приборы измеряют не среднее, а действующее напряжение, которое эквивалентно постоянному по энергии. Связь среднего и действующего напряжения дает коэффициент формы кф = Uэфф / Uср . Для меандра он равен 1, для синуса 1,11.
Отсюда эффективное напряжение на катушке: Uэфф = 4 ⋅ кф ⋅ n ⋅ Sc ⋅ Bm ⋅ f
Габаритную мощность оценим из следующих соображений. Частота f не велика, потери на вихревые токи и перемагничивания малы и мощность ограничена лишь перегревом обмотки. Его определяет максимальная плотность тока j , одинаковая для обоих обмоток.
Определим габаритную мощность как полусумму мощностей первичной и вторичной обмоток.
Pгаб = ( P1+P2 ) / 2 = ( Uэфф1⋅ I1 + Uэфф2 ⋅ I2 ) / 2 = j ( S1 n1 + S2 n2 ) 4 кф Sc Bm f / 2
Где S1 и S2 площади витка первичной и вторичной обмоток.
Это соотношение можно записать через площадь меди Sm:
Pгаб = 2⋅ кф ⋅ f ⋅ Sc ⋅ Sm ⋅ Bm ⋅ j
Площадь меди связывают с коэффициентом заполнения окна σ = Sm / Sо.
Сигма это некий эмпирический коэффициент, равен минимум 0,15 для однослойной обмотки и максимум 0,4 для многослойной (больше не поместится).
В итоге наша формула имеет вид:
Pгаб = 2 ⋅ кф ⋅ σ⋅ f ⋅ Sc⋅ Sо ⋅ Bm ⋅ j
Все величины здесь в СИ.
Допустим, что напряжение имеет форму меандра, кф = 1. Выбирая плотность тока j = 2,2 А / мм2 ; коэффициент заполнения σ = 0,15 ; выразив площади в см2 ; Bm в Тл ; частоту в Гц получим расчетную формулу:
Pгаб = Sc ⋅ So ⋅ f ⋅ Bm / 150
Как видно, эта формула выведена с большим запасом, реально можно получить с трансформатора и большую мощность.
Литература.
- Косенко С. “Расчёт импульсного трансформатора двухтактного преобразователя” // Радио, №4, 2005, с. 35 — 37, 44.
- Эраносян С. А. Сетевые блоки питания с высокочастотными преобразователями. — Л.: Энергоатомиздат. Ленингр. отд-ние, 1991,— 176 с: ил.
- С. В. Котенёв, А. Н. Евсеев. Расчет и оптимизация тороидальных трансформаторов и дросселей. — М.: Горячая линия-Телеком, 2013. — 359 с.: ил.
- А. Петров «Индуктивности, дроссели, трансформаторы «// Радиолюбитель, №12, 1995, с.10-11.
- Михайлова М.М., Филиппов В.В., Муслаков В.П. Магнитомягкие ферриты для радиоэлектронной аппаратуры. Справочник. — М.: Радио и связь, 1983. — 200 с., ил.
- Расчетные геометрические параметры кольцевых сердечников.
- Б.Ю.Семенов. Силовая электроника для любителей и профессионалов. М. : Солон-Р, 2001. — 327 с. : ил
- Курс лекций «Импульсная техника» для студентов 4-го курса кафедры Радиофизики. Глава 3.
Физическое понятие индуктивности обмоток
Индуктивность представляет собой коэффициент пропорциональности между током, создаваемым замкнутым электрическим контуром, и магнитным потоком, который создается этим контуром.
Более понятной формулировкой будет та, которая говорит о величине ЭДС самоиндукции в замкнутом контуре, которая возникает при изменении силы тока за единицу времени. То есть, понятие индуктивности справедливо для изменяющегося тока.
При постоянном токе говорить об индуктивности бессмысленно.
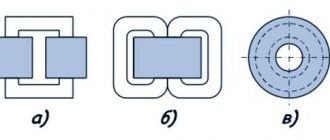
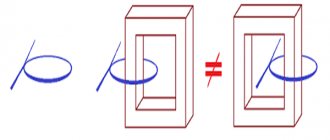
В идеальном трансформаторе все электромагнитное поле, создаваемое обмотками, замкнуто в магнитном сердечнике. В реальных конструкциях существует поле рассеяния, величина которого зависит от способа выполнения катушки и конструктивных особенностей сердечника. Чем больше толщина намотки, тем большая часть электромагнитного поля замыкается вне магнитопровода.
Этому способствует также качество сборки магнитопровода. Зазоры между пластинами способствуют резкому увеличению рассеивания. В связи с этим наилучшими свойствами обладают О-образные сердечники.
От чего зависит ЭДС в обмотках трансформатора?
В прошлой статье я указал, что мгновенное значение ЭДС в обмотке трансформатора определяется числом витков ω провода в ней и скоростью изменения магнитного потока dΦ/dt
где ω – число витков обмотки трансформатора,
dФВ/dt – скорость изменения магнитного потока.
Однако в большинстве случаев нам интересно не мгновенное значение ЭДС, а действующее. Поэтому выведем выражение, определяющее действующее значение ЭДС в обмотках трансформатора. Это можно сделать аналитически проинтегрировав функцию изменения магнитного потока dΦ/dt, либо же путем нахождения среднего значения ЭДС Ecp и коэффициента формы ЭДС kф. Я буду выводить выражение вторым способом.
Магнитный поток протекая в сердечнике трансформатора изменяется в соответствии с некоторой периодичной функцией имеет два амплитудных значения максимальное +Фm и минимальное –Фm, тогда полное изменение магнитного потока за полупериод Т/2 будет иметь значение
Тогда среднее значение ЭДС Еср в обмотке трансформатора будет иметь вид
где ω – число витков обмотки трансформатора,
Т/2 – полупериод изменения функции магнитного потока,
f – частота изменения магнитного потока,
Фm – амплитуда магнитного потока.
Действующее значение ЭДС и её среднее значение связывает коэффициент формы кривой ЭДС kф, тогда действующее значение ЭДС в обмотке трансформатора будет определяться следующим выражением
где kф – коэффициент формы ЭДС,
f – частота изменения ЭДС,
ω – число витков обмотки трансформатора,
B – магнитная индукция в сердечнике,
Sc – площадь сечения сердечника трансформатора.
Приведём примеры действующего значение ЭДС для синусоидального, прямоугольного (меандр) и треугольного изменения
Из вышесказанного следует, что при условии постоянства электромагнитной индукции B, ЭДС пропорциональна конструктивным параметрам трансформатора сечению магнитопровода Sc и количеству витков ω. Правильный выбор величины электромагнитной индукции В является одной из ключевых задач при проектировании трансформатора. Кроме того, с ростом частоты f увеличивается ЭДС, поэтому для реализации одинаковой ЭДС с ростом частоты требуются меньшие размеры и вес трансформатора. Данный фактор является основным преимуществом трансформаторов высокой частоты, которые чаще всего применяются в настоящее время.
Формулы и измерение
Формулы для расчета индуктивности катушек довольно сложны и имеет различный вид для различных типов исполнения обмоток:
- линейный проводник;
- одновитковая катушка;
- плоская катушка;
- соленоидальная обмотка;
- тороидальная форма.
Наибольшие сложности возникают при расчетах многовитковых многослойных катушек, то есть тех, которые составляют обмотку трансформаторов.
В подавляющем большинстве случаев точный расчет невозможен, поэтому приходится использовать примерные данные и уточнять их после проведения измерений.
Формулы для расчета индуктивности трансформатора основаны на расчетах соленоида:
L=µ0µN2S/l, где
µ0 – магнитная постоянная;
µ – магнитная проницаемость сердечника;
N – количество витков;
S – площадь одного витка;
l – длина обмотки.
Для измерения индуктивности существует несколько методик и приборов, созданных на их основе. В большинстве случаев измерение производится путем вычислений индуктивного сопротивления катушки при подаче образцового напряжения заданной частоты и измеренного значения тока через обмотку.
В специализированных приборах вычисления производятся автоматически, и пользователь только считывает показания шкалы прибора, выраженные в единицах индуктивности – Гн, мГн или мкГн.
Условное обозначение трансформаторов на схемах:
Рисунок 1 — УГО трансформаторов.
- – трансформатор с ферритовым сердечником;
- – трансформатор с сердечником из магнитодиэлектрика, т.е. диэлектрического магнитного материала;
- – трансформатор с ферритовым сердечником с 2 вторичными обмотками;
- – трансформатор с ферритовым сердечником с отводами из вторичной обмотки.
Рядом с условным обозначением указывается тип элемента (T) и порядковый номер, также рядом с условным обозначением может указываться (не является обязательным требованием) коэффициент трансформации.
Как измерить в домашних условиях
Приборы для непосредственного измерения индуктивности имеют высокую стоимость и редко используются в домашних условиях. С приемлемой точностью результаты можно получить, используя обычные приборы для измерения переменного тока: амперметр и вольтметр. Также необходим омметр.
Порядок действий следующий:
- При помощи омметра определяют активное сопротивление обмотки R.
- Подключают трансформатор последовательно с амперметром в сеть.
- Параллельно обмотке подключают вольтметр.
- По показаниям приборов определяют полное сопротивление трансформатора: Z=U/I
- Индуктивное сопротивление находят, вычитая из полного сопротивления активное: XL=Z-R
- Индуктивность определяется по формуле: L=XL/(2πf), где π – число пи 3.14, f – частота измерений.
Как правило, активное сопротивление намотки значительно (на несколько порядков) меньше индуктивного, поэтому можно его не учитывать. Именно поэтому, включение трансформатора в цепь постоянного напряжения вызывает короткое замыкание. Ток обмотки при этом будет ограничиваться только активным сопротивлением.
Маркировка трансформаторов:
Так как габариты даже высокочастотных трансформаторов не такие уж и маленькие, по сравнению с остальными электронными приборами, то информация обычно указывается в явном виде.
На трансформаторах указывается:
- Тип трансформатора, например, ТП – трансформатор питания (т.е. силовой);
- Рабочее напряжение первичной и всех вторичных обмоток;
- Указывается либо номинальная мощность, либо максимальный ток для каждой вторичной обмотки;
- Число вторичных обмоток;
- Рабочая частота;
- Для измерительных трансформаторов указывается классточности;
- Для согласующих трансформаторов указывается индуктивность обмоток.
Физические особенности процесса
Оптимальная величина потока определяется особенностями устройства. Проходя путь от генератора (места выработки) до потребителя, электрическая энергия трансформируется. В генераторе показатели выше, так как проходить ток будет большие расстояния (от 1-10 метров, до 1-10 км). Нормативные показатели – 10 кВ. Потребитель по установленным правилам должен получить электроэнергию, мощность которой равна 380 или 220 В. Добиться необходимых изменений позволяет трансформатор с вращающимся магнитным полем.
Пусковой режим работы трансформатора на резонансную нагрузку
Пусковой режим должен обеспечивать нормальный переходный процесс и выход рабочей точки петли гистерезиса на симметричный частный цикл в рабочем режиме. Если изначально магнитопровод силового трансформатора был полностью размагничен, при подаче на трансформатор напряжения с частотой резонансного контура центр частного цикла петли намагничивания смещается по основной кривой намагничивания из точки О в точку О1, поэтому рабочая индукция оказывается увеличенной по отношению к своему установившемуся значению в два раза (рис. 11а).
Моделирование переходного процесса при пуске показало, что происходит размагничивание трансформатора (рис. 11б) с постоянной времени τ, определяемой выражением (4). При этом видно, что величина перерегулирования индукции трансформатора достигает удвоенного значения. Для устранения перерегулирования пуск инвертора рекомендуется производить с повышенной частоты, соответственно в два раза превышающей резонансную. По мере размагничивания силового трансформатора частота может быть итерационно приближена к резонансной, при этом величина шага подстройки не должна приводить к превышению рабочей индукции (рис. 11в).
Рис. 11. Переходной процесс при пуске трансформатора: а) первый цикл петли намагничивания; б) процесс размагничивания трансформатора; в) нормальный пуск трансформатора
Процесс подмагничивания трансформатора
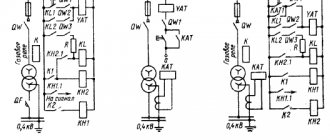
Типовая структура преобразователя частоты для установки индукционного нагрева, построенная на основе последовательного резонансного инвертора напряжения, нагруженного через согласующий трансформатор TV1 на последовательный резонансный контур, образованный индуктором с нагреваемой деталью, имеющей активно-индуктивное сопротивление (Rн, Lи), и компенсирующим конденсатором С, изображена на рис. 1. В процессе нагрева параметры нагрузки существенно изменяются, что приводит к изменению резонансной частоты колебательного контура, в связи с этим в систему управления преобразователя частоты вводится узел фазовой автоподстройки частоты, непрерывно настраивающий инвертор на резонансную частоту. При этом возможно однократное появление несимметрии при изменении длительности одного из полупериодов питающего напряжения, которая определяется отношением длительности шага подстройки к резонансному периоду.
Рис. 1. Типовая схема преобразователя частоты УИН
Если к согласующему силовому трансформатору TV1 прикладывается симметричное прямоугольное напряжение, его магнитопровод перемагничивается по симметричной частной петле гистерезиса (рис. 2) и магнитная индукция в нем изменяется от значения +Bр до значения –Bр. Однако разброс динамических параметров IGBT-транзисторов, согласующих драйверов и системы фазовой автоподстройки частоты приводит к неодинаковой длительности полупериодов выходного напряжения и, как следствие, к появлению постоянной составляющей напряжения, прикладываемого к трансформатору Uср и подмагничиванию силового трансформатора постоянным током [1], величину которого можно определить соотношением
где
— среднее значение напряжения на первичной обмотке в течение резонансного периода Т, Rоб1 — сопротивление первичной обмотки. Это приводит к смещению центра частной петли гистерезиса по основной кривой намагничивания из точки О в точку О1 (рис. 2), соответствующую напряженности поля Н0 от намагничивающей силы постоянного тока. Н0 определяется согласно закону полного тока
где W — количество витков первичной обмотки; lc — длина силовой магнитной линии трансформатора.
Рис. 2. Смещение частной петли гистерезиса магнитопровода силового трансформатора при наличии подмагничивания постоянным током
Таким образом, ток ILμ индуктивности намагничивания трансформатора Lμ можно условно разделить на переменную составляющую, обеспечивающую перемагничивание магнитопровода, и постоянную составляющую, называемую током подмагничивания I0 и определяемую величиной постоянной составляющей напряжения несимметрии Uср.
Подмагничивание силового трансформатора приводит к перемагничиванию его сердечника по несимметричному циклу (кривая 2), что при достаточном значении тока подмагничивания приводит к насыщению силового трансформатора и неограниченному росту тока первичной обмотки, несмотря на малое значение Вр (рис. 3). В результате этого происходит перегрузка и выход из строя силовых транзисторов инвертора.
Рис. 3. Подмагничивание магнитопровода постоянным током: а) ток первичной обмотки; б) ток намагничивания трансформатора
Известные в настоящее время методы решения проблем подмагничивания силового трансформатора условно можно свести к четырем группам:
- Введение обратной связи по потоку рассеяния или току намагничивания силового трансформатора. В этом случае, при увеличении тока подмагничивания, коррекция длительности управляющих импульсов должна производиться в каждом такте управления [4].
- Выбор магнитопровода трансформатора с непрямоугольной формой петли намагничивания [3]. При этом следует отметить, что чем больше длина магнитной силовой линии и меньше магнитная проницаемость ферромагнитного материала магнитопровода, тем более силовой трансформатор становится устойчивым к подмагничиванию постоянным током (рис. 2), так как постоянная составляющая индукции (Bo), вызванная током подмагничивания (Io), оказывается значительно меньше диапазона изменения рабочей индукции (Bp).
- Введение немагнитного зазора в магнитопровод трансформатора, имеющего мощный размагничивающий эффект, приводящий к сдвигу петли гистерезиса и заметному снижению магнитной проницаемости высокопроницаемых материалов при уменьшении остаточной индукции Br. В связи с этим значительно увеличивается полезный размах индукции [3]. Малые величины зазора фактически не влияют на потери в магнитопроводе, однако оказывают необходимый размагничивающий эффект, исключающий быстрое насыщение магнитопровода при воздействии поля постоянного тока.
- Включение разделительного конденсатора в первичную обмотку трансформатора (рис. 5), что приводит к симметрированию положения рабочей петли гистерезиса. В этом случае ток подмагничивания силового трансформатора полностью отсутствует за счет того, что среднее значение тока разделительного конденсатора в установившемся режиме равно нулю.
При сопоставлении данных методов следует отметить следующие особенности их реализации. Первый метод является универсальным, однако на практике он связан со значительными сложностями измерения контролируемых параметров (потока рассеивания и тока подмагничивания). К тому же при значительной несимметрии рост тока через первичную обмотку трансформатора в каждом периоде происходит с большой скоростью, что может привести к ситуации, когда ограничение длительности импульсов не успевает скорректировать несимметрию [4].
Второй метод наиболее простой, но его применение не исключает ток подмагничивания, вследствие чего приходится увеличивать запас рабочей индукции по отношению к индукции насыщения, которая должна включать постоянный уровень Bo, обусловленный током подмагничивания.
Введение немагнитного зазора является эффективным методом борьбы с подмагничиванием магнитопровода и позволяет уменьшить смещение частного цикла петли намагничивания при воздействии значительных несимметрий. Однако в этом случае, как и в предыдущем, полностью устранить ток подмагничивания не удается.
В резонансных схемах наиболее эффективен четвертый метод, который полностью исключает ток подмагничивания трансформатора, благодаря чему удается симметрировать частный цикл петли гистерезиса при воздействии значительных несимметрий и сравнительно малом запасе рабочей индукции.