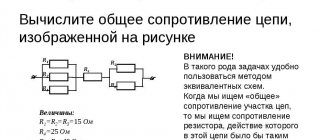
Часто бывает, что задачу не удается решить из-за того, что под рукой нет нужной формулы. Выводить формулу с самого начала – дело не самое быстрое, а у нас на счету каждая минута.
Ниже мы собрали вместе основные формулы по теме «Электричество и Магнетизм». Теперь, решая задачи, вы сможете пользоваться этим материалом как справочником, чтобы не терять время на поиски нужной информации.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Магнетизм: определение
Магнетизм – это взаимодействие движущихся электрических зарядов, происходящее посредством магнитного поля.
Поле – особая форма материи. В рамках стандартной модели существует электрическое, магнитное, электромагнитные поля, поле ядерных сил, гравитационное поле и поле Хиггса. Возможно, есть и другие гипотетические поля, о которых мы пока что можем только догадываться или не догадываться вовсе. Сегодня нас интересует магнитное поле.
Магнитная индукция
Так же, как заряженные тела создают вокруг себя электрическое поле, движущиеся заряженные тела порождают магнитное поле. Магнитное поле не только создается движущимися зарядами (электрическим током), но еще и действует на них. По сути магнитное поле можно обнаружить только по действию на движущиеся заряды. А действует оно на них с силой, называемой силой Ампера, о которой речь пойдет позже.
Изображение магнитного поля при помощи силовых линий
Прежде чем мы начнем приводить конкретные формулы, нужно рассказать про магнитную индукцию.
Магнитная индукция – это силовая векторная характеристика магнитного поля.
Она обозначается буквой B и измеряется в Тесла (Тл). По аналогии с напряженностью для электрического поля Е магнитная индукция показывает, с какой силой магнитное поле действует на заряд.
Кстати, вы найдете много интересных фактов на эту тему в нашей статье про теорию магнитного поля и интересные факты о магнитном поле Земли.
Как определять направление вектора магнитной индукции? Здесь нас интересует практическая сторона вопроса. Самый частый случай в задачах – это магнитное поле, создаваемое проводником с током, который может быть либо прямым, либо в форме окружности или витка.
Для определения направления вектора магнитной индукции существует правило правой руки. Приготовьтесь задействовать абстрактное и пространственное мышление!
Если взять проводник в правую руку так, что большой палец будет указывать на направление тока, то загнутые вокруг проводника пальцы покажут направление силовых линий магнитного поля вокруг проводника. Вектор магнитной индукции в каждой точке будет направлен по касательной к силовым линиям.
Определение
Учёный, открывший данный закон, — настоящая загадка истории: про него известно лишь то, что фамилия у него была Буравчик. Большинство склоняются к тому, что звали его всё-таки Пётр Сигизмундович. Про него сочиняют немало баек.
Даже с появлением закона буравчика связана забавная полушутка-полулегенда: якобы когда Буравчик смог сформулировать это правило (правда, название было не в честь его автора, а в честь тех предметов, которые действовали согласно данному закону), он отправился прямиком в Москву, на поклон к Михаилу Васильевичу Ломоносову. Простота метода несколько смутила великого учёного, и он, погрузившись в размышления, отвернулся и начал, извините за выражение, ковыряться в носу.
На что Пётр Сигизмундович ехидно заметил, что Михаил Васильевич, используя свой палец как буравчик, в точности следует его закону.
После этого Ломоносов уже не колебался в принятии решения относительно изысканий Буравчика: правилу — быть! Каждый физик формулирует это правило своими словами, однако суть всегда такова: если направление движения штопора будет проходить в одну и ту же сторону с направлением тока внутри проводника, то его ручка продемонстрирует сторону, в которую будет обращён вектор магнитной индукции.
В свою очередь, штопор интерпретировался в правило правой руки, которое, в свою очередь, послужило основой для другого мнемонического закона, правила левой руки, благодаря коим физика кажется намного проще. Всех их активно применяют во многих её областях — в этом немалую роль играет их простота вкупе с эффективностью, которые были отмечены ещё Ломоносовым, а также то, что звучат они кратко и понятно: с помощью правила буравчика можно определить, к примеру, сторону, в которую направлены угловая скорость, магнитная индукция, параметры индукционного тока и многое другое, что позволяет решать задачи. В этой статье мы подробно рассмотрим все случаи этих правил и правила винта.
Сила Ампера
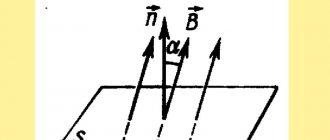
Представим, что есть магнитное поле с индукцией B. Если мы поместим в него проводник длиной l, по которому течет ток силой I, то поле будет действовать на проводник с силой:
Это и есть сила Ампера. Угол альфа – угол между направлением вектора магнитной индукции и направлением тока в проводнике.
Направление силы Ампера определяется по правилу левой руки: если расположить левую руку так, чтобы в ладонь входили линии магнитной индукции, а вытянутые пальцы указывали бы направление тока, отставленный большой палец укажет направление силы Ампера.
Правило буравчика для момента
Момент сил — это вектор силы, которая вызывает вращательное движение какого-то объекта. Вращательный момент связан с другими величинами, например, работой, совершаемой во время вращения тела. Хоть алгоритм и работает аналогично, сформулируем правило винта (буравчика) для момента силы. Если прокручивать штопор туда, куда силы смещают тело, то направление завинчивания инструмента укажет направление вращательного момента. Для правой руки правило звучит так: мысленно взяв предмет в правую руку, предмет двигают в сторону направления четырех пальцев (их ориентация должна совпадать с той стороной, куда силы пытаются сместить объект), большой распрямленный палец же укажет вектор вращающего момента.
Сила Лоренца
Мы выяснили, что поле действует на проводник с током. Но если это так, то изначально оно действует отдельно на каждый движущийся заряд. Сила, с которой магнитное поле действует на движущийся в нем электрический заряд, называется силой Лоренца. Здесь важно о, так на неподвижные заряды магнитное поле не действует.
Итак, частица с зарядом q движется в магнитном поле с индукцией В со скоростью v, а альфа – это угол между вектором скорости частицы и вектором магнитной индукции. Тогда сила, которая действует на частицу:
Как определить направление силы Лоренца? По правилу левой руки. Если вектор индукции входит в ладонь, а пальцы указывают на направление скорости, то отогнутый большой палец покажет направление силы Лоренца. Отметим, что так направление определяется для положительно заряженных частиц. Для отрицательных зарядов полученное направление нужно поменять на противоположное.
Если частица массы m влетает в поле перпендикулярно линиям индукции, то она будет двигаться по окружности, а сила Лоренца будет играть роль центростремительной силы. Радиус окружности и период обращения частицы в однородном магнитном поле можно найти по формулам:
Электромагнитные явления (стр. 5 )
Если увеличить силу пробного тока или длину элемента в некоторое число раз, то в это же число раз изменится и сила, действующая на пробный элемент тока.
Отношение же силы, действующей на пробный элемент тока, к произведению силы тока на длину элемента останется величиной постоянной, не зависящей ни от силы, ни от величины тока, ни от длины элемента. Это отношение обозначается буквой В
и принимается за силовую характеристику магнитного поля. Соответствующая физическая величина называется
ИНДУКЦИЕЙ МАГНИТНОГО ПОЛЯ
.
ИНДУКЦИЯ МАГНИТНОГО ПОЛЯ – это векторная физическая величина, равная отношению силы, действующей на элемент длины проводника, помещенный в данную точку поля, к произведению силы тока на длину элемента.
МОДУЛЬ ВЕКТОРА МАГНИТНОЙ ИНДУКЦИИ РАВЕН:
Индукция магнитного поля показывает, чему равна сила, действующая на элемент проводника с током единичной длины, если по нему идет ток единичной силы.
Чтобы получить единицу индукции магнитного поля, надо в определяющее уравнение индукции подставить единицы силы — 1Н, силы тока — 1А, длины — 1м. Получаем: .
Эта единица имеет собственное наименование 1Тл (
1 тесла).
Для наглядности магнитные поля на чертежах изображаются с помощью силовых линий.
СИЛОВЫЕ ЛИНИИ МАГНИТНОГО ПОЛЯ — это линии, касательные к каждой точке которых совпадают с вектором индукции магнитного поля.
Направление силовых линий магнитного поля определяется по ПРАВИЛУ БУРАВЧИКА
(или
ПРАВОГО ВИНТА
):
ЕСЛИ БУРАВЧИК ВРАЩАТЬ ТАК, ЧТОБЫ ОН ПРОДВИГАЛСЯ ПО ТОКУ, ТО НАПРАВЛЕНИЕ ВРАЩЕНИЯ РУЧКИ БУРАВЧИКА СОВПАДАЕТ С НАПРАВЛЕНИЕМ СИЛОВЫХ ЛИНИЙ МАГНИТНОГО ПОЛЯ
.
По густоте силовых линий можно сравнивать индукции различных магнитных полей.
Величина индукции магнитного поля прямого БЕСКОНЕЧНО ДЛИННОГО тока в данной точке поля прямо пропорциональна силе тока, создающего это поле, и обратно пропорциональна расстоянию от этого тока до данной точки поля:
Чтобы найти значение силы (называемой СИЛОЙ АМПЕРА
), действующей на проводник, помещенный в магнитное поле, надо знать величину индукции магнитного поля, силу тока, протекающего по проводнику, длину проводника и угол между направлением силы тока и вектором индукции магнитного поля.
Направление силы Ампера определяется по ПРАВИЛУ ЛЕВОЙ РУКИ: ЕСЛИ ЛАДОНЬ ЛЕВОЙ РУКИ РАСПОЛОЖИТЬ ТАК, ЧТОБЫ В НЕЕ ВХОДИЛИ ЛИНИИ ИНДУКЦИИ МАГНИТНОГО ПОЛЯ, ЧЕТЫРЕ ПАЛЬЦА НАПРАВИТЬ ПО ТОКУ (ИЛИ ПРОТИВ ДВИЖЕНИЯ ОТРИЦАТЕЛЬНЫХ ЗАРЯДОВ), ТО ОТОГНУТЫЙ НА 90 ГРАДУСОВ БОЛЬШОЙ ПАЛЕЦ ПОКАЖЕТ НАПРАВЛЕНИЕ СИЛЫ, ДЕЙСТВУЮЩЕЙ НА ПРОВОДНИК
Если сила Ампера — это сила, действующая со стороны магнитного поля на все заряженные частицы, совершающие направленное движение внутри проводника, то сила Лоренца — это сила, действующая со стороны магнитного поля на отдельно взятую движущуюся заряженную частицу.
, где N — число заряженных частиц, движущихся внутри проводника.
Сила тока I
может быть представлена через заряд q всех частиц и время
t
, в течение которого этот заряд протекает через поперечное сечение проводника: .
Заряд всех частиц, в свою очередь, равен произведению заряда одной частицы q0
на число частиц
N
:
q=q0N.
Таким образом:
Направление силы Лоренца так же, как и сила Ампера, определяется по правилу левой руки.
Если магнитное поле в точке создается несколькими токами, то результирующая индукция находится как векторная сумма индукций полей, создаваемых каждым током независимо от других токов. Это правило носит название ПРИНЦИПА СУПЕРПОЗИЦИИ МАГНИТНЫХ ПОЛЕЙ.
Если под действием силы Ампера проводник перемещается в магнитном поле, то магнитное поле совершает работу. Величина этой работы зависит от силы тока, протекающего по проводнику и от магнитного потока, пронизывающего площадь, ометаемую движущимся проводником.
МАГНИТНЫЙ ПОТОК определяется как физическая величина, равная произведению перпендикулярной составляющей индукции магнитного поля на площадь, которую оно пронизывает:
Чтобы получить единицу магнитного потока, надо в его определяющее уравнение подставить единицы индукции — 1Тл и площади – 1 м2. Получаем:
Эта единица имеет собственное наименование 1 Вб (1вебер).
§3. Вещества в магнитном поле
Известно, что магнитные поля можно получить с помощью проводников, по которым течет ток, и постоянных магнитов. Материалом, для изготовления постоянных магнитов служат специальные сорта стали, некоторые сплавы. Эти же и некоторые другие вещества могут значительно увеличивать индукцию магнитного поля тока.
Возникает вопрос: ЧЕМ ЖЕ ВЕЩЕСТВА С ЯРКО ВЫРАЖЕННЫМИ МАГНИТНЫМИ СВОЙСТВАМИ ОТЛИЧАЮТСЯ ОТ ДРУГИХ ВЕЩЕСТВ?
Ответить на этот вопрос можно, только разобравшись в природе магнетизма вообще.
Для этого можно оттолкнуться от гипотезы Ампера о существовании в любом теле молекулярных, точнее внутриатомных токов.
Согласно этой гипотезе, магнитные свойства должны быть присущи всем телам без исключения.
Одна из правдоподобных версий, позволяющих представить себе механизм намагничивания веществ, заключается в предположении, что магнитное поле у атома появляется за счет орбитального движения электронов.
Если это так, то, вероятно, должно существовать два класса веществ с нескомпенсированными и со скомпенсированными магнитными полями у их отдельных атомов.
При попадании веществ, относящихся к первой группе, в магнитное поле, последнее будет выстраивать атомы так, что векторы индукции внешнего поля и каждого атома окажутся сонаправленными. За счет этого внешнее магнитное поле должно уменьшаться.
Магнитная проницаемость таких веществ больше единицы и они будут слабо втягиваться в магнитное поле.
Опыт показывает, что подобные вещества действительно существуют. Они называются ПАРАМАГНЕТИКАМИ.
У веществ другого класса число электронов в атомах должно быть четным. При этом, если на одной орбите будет находиться два электрона, вращаться они должны в разные стороны.
В этом случае понятно, что векторы индукции магнитного поля, создаваемого каждым таким электроном, будут равны по величине и противоположны по направлению. При любой ориентации атомов, вещества такого типа магнитными свойствами обладать не должны.
Если же подобные вещества попадут в магнитное поле, ситуация меняется.
На вращающиеся электроны будет действовать сила Лоренца, причем, поскольку электроны движутся в разные стороны, сила, действующая на них, также будет направлена в разные стороны.
За счет этого должны измениться численные значения скоростей электронов. У одного электрона скорость увеличится, у другого – уменьшится.
Соответственно изменится и индукция магнитных полей, создаваемых электронами. У атома появится собственное магнитное поле и направлено оно будет против поля, вызвавшего описанный эффект.
Магнитная проницаемость таких веществ меньше единицы и они будут слабо выталкиваться из магнитного поля.
Опыт показывает, что существуют и такие вещества. Они называются ДИАМАГНЕТИКАМИ
.
Разработанная модель позволяет понять природу магнетизма и является необходимым шагом для ответа на поставленный в начале вопрос.
Кроме описанных ситуаций, можно представить еще один случай, когда в веществе имеются локальные области намагниченности, где магнитные поля огромного количества атомов уже направлены в одну сторону.
Суммарное магнитное поле многих локальных областей может быть равно нулю, если эти области в теле сориентированы по-разному.
С ростом внешнего магнитного поля, за счет перестройки атомов, области намагниченностей, не совпадающих с этим полем, будут уменьшаться, а совпадающих расти.
Магнитная проницаемость таких материалов должна быть очень большой.
Такие вещества называют ФЕРРОМАГНЕТИКАМИ
.
Ферромагнетики находят очень широкое применение в технике. Из них изготовляют постоянные магниты и электромагниты, сердечники трансформаторов и генераторы тока, ими покрывают пленки для магнитофонов и диски для ЭВМ.
Согласно изложенному механизму, предметы, изготовленные из ферромагнетиков можно намагнитить, поместив их во внешнее магнитное поле.
Действительно, даже в относительно слабом магнитном поле Земли удается намагнитить стальной стержень, сориентировав его в направлении линий магнитной индукции и ударяя по торцу молотком.
Если ферромагнетики можно намагничивать, то вероятно, можно осуществлять и обратный процесс их размагничивания, например, за счет увеличения интенсивности теплового движения частиц.
Опыт с нагреванием намагниченной стальной иглы подтверждает это предположение.
Аналогичные опыты с другими ферромагнетиками показывают, что у всех них при некоторой температуре, разной для разных веществ, и называемой ТОЧКОЙ КЮРИ
, пропадают ферромагнитные свойства.
§4. Некоторые применения магнитных явлений
С магнитными явлениями мы встречаемся и в жизни, широко применяют их и в технике.
Поскольку магнитным полем обладает Земля, магнитная стрелка может дать возможность ориентироваться на ее поверхности.
Сильное магнитное поле можно получить с помощью катушки с током, в которую вставлен стальной сердечник. Такое устройство называется ЭЛЕКТРОМАГНИТОМ
.
Намагниченные пленки, покрытые специальным составом, могут очень долгое время хранить на себе различную информацию.
Но не всегда магнитные явления используются на пользу человеку.
Так, в военном деле применяют мины, реагирующие на магнитные поля, создаваемые намагниченными стальными корпусами кораблей.
Чтобы не подорваться на таких минах корабли необходимо размагничивать. Эту операцию можно осуществить с помощью проводников, по которым пропускается электрический ток определенной силы и направления, в зависимости от характера намагниченности корабля.
ПРИМЕР РЕШЕНИЯ ЗАДАЧИ
В горизонтальной плоскости на параллельно расположенных токопроводящих рельсах, расстояние между которыми L
, лежит проводник.
Вся система помещена в магнитное поле с индукцией В
.
Ток какой силы необходимо пропускать через проводник, чтобы он двигался по рельсам с постоянной скоростью?
Коэффициент трения скольжения проводника по рельсам — m
. Углы между вектором индукции магнитного поля, направлением тока в проводнике и скоростью его движения — прямые.
Эту задачу можно отнести к разряду статических, по той причине, что проводник, по условию задачи, должен двигаться с постоянной скоростью.
Тело движется с постоянной скоростью, если сумма сил, действующих на него, равна нулю.
Если по проводнику, находящемуся в магнитном поле, течет ток силой I
, на проводник действует сила Ампера.
Направление этой силы можно определить по правилу левой руки. Для этого необходимо левую руку расположить таким образом, чтобы силовые линии входили в ладонь.
Четыре пальца должны быть направлены по току, тогда отогнутый на 900 большой палец, покажет направление силы Ампера.
Если проводник движется с постоянной скоростью, то должна существовать сила, направленная в противоположную сторону и равная по величине силе Ампера.
| В + + + I + + + FА Fтр + + + + + + + + + + |
Так как между проводником и рельсами присутствует трение, то вероятно, такой силой может быть сила трения скольжения.
Сумма сил, действующих на проводник равна нулю, значит сила Ампера равна силе трения:
Как только мы записали это равенство, достаточно вспомнить, что сила Ампера равна произведению силы тока, протекающего по проводнику, на длину активной части проводника, находящегося в магнитном поле, и индукцию магнитного поля:
Поскольку угол между вектором магнитной индукции и направлением тока равен 900, то sin900 = 1.
Сила трения равна произведению коэффициента трения на силу нормального давления:
Если рельсы расположены горизонтально, то сила нормального давления равна силе тяжести:
Подставляем выражение для силы Ампера и силы трения в исходное уравнение и получаем выражение, из которого можно найти интересующую нас величину силы тока: .
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Задача №1
Пройдя разность потенциалов 2000 В, электрон влетает в однородное магнитное поле с индукцией 150 мТл и движется в нем по дуге окружности радиусом 1 м (в плоскости, перпендикулярной магнитному полю).
Чему равно отношение заряда электрона к его массе (удельный заряд электрона).
Задача №2
На двух тонких нитях висит горизонтальный стержень длиной L
и массой
m
. Стержень находится в однородном магнитном поле, вектор индукции которого направлен вертикально вниз. На какой угол отклонится нить, если по стержню пропустить ток силой
I
?
Задача №3
В горизонтально расположенном проводнике длиной 20 см и массой 4 г сила тока равна 10 А. Найдите индукцию (модуль и направление) магнитного поля, в которое нужно поместить проводник, чтобы сила тяжести уравновесилась силой Ампера.
Задача №4
Электрон движется в однородном магнитном поле с индукцией В =
4 мТл. Найдите период обращения электрона.
Задача №5
В проводнике с длиной активной части 8 см сила тока равна 50 А. Он находится в однородном магнитном поле. Под действием силы Ампера проводник переместился на 10 см перпендикулярно силовым линиям, и при этом была совершена работа 8 мДж. Найдите индукцию магнитного поля.
Глава 5
ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ
В 1820 г. датский физик экспериментально установил связь между электрическим током и магнитным полем. Суть опытов Эрстеда состояла в том, что если по проводнику проходил электрический ток, вокруг проводника возникало магнитное поле, которое можно было исследовать с помощью магнитной стрелки.
Говоря не очень точным языком, науки того времени, когда впервые были проведены аналогичные опыты, «Электричество порождало магнетизм».
Открытие Эрстеда, сделанное в результате простого эксперимента, послужило толчком к развитию нового направления в естествознании — учения об электромагнетизме. Кроме того, что это открытие повлекло за собой цепь новых фундаментальных экспериментов в области исследования связей между электрическими и магнитными явлениями (изучение взаимодействия параллельных токов А. Ампером), оно привело к ряду важнейших изобретений, в частности, электромагнита (1820 г., Ф. Араго), электродвигаг., М. Фарадей) и дало объективный метод измерения электричества, оно натолкнуло целый ряд естествоиспытателей на мысль:
если электричество порождает магнетизм, то не может ли магнетизм породить электричество?
Именно так поставили себе задачу: найти связь между магнетизмом и электричеством А. Ампер и М. Фарадей. Но Ампер от решения задачи вскоре отказался и даже пытался убедить Фарадея последовать его примеру. Однако упорство Фарадея вызывает удивление и восхищение. Будучи убежденным в существовании не только прямой связи между электричеством и магнетизмом, но связи обратной, он искал эту связь 11 лет. Разумеется, Фарадей в течение этого времени не замыкался только на решении этой задачи, он выполнял множество других дел и решал другие задачи. Поиск затруднялся и из-за отсутствия необходимых для экспериментов материалов. В распоряжении Фарадея не было даже обычного для нас провода с изоляцией. Не было у него и чувствительных приборов, способных зарегистрировать слабые эффекты, которые он искал. В ряде случаев Фарадей подходил исключительно близко к открытию, затем вновь удалялся от него.
Аналогичным образом обстояли дела и у других исследователей. Истории науки известен поистине печальный для одного из ее представителей факт. В 1825 г. Колладон проводил эксперимент, который давал тот же результат, что в дальнейшем получил Фарадей. Однако в целях исключения влияния мощного магнита на электроизмерительный прибор, последний был перенесен в другую комнату. К тому времени, когда Колладон доходил до прибора, всякое движение его стрелки прекращалось. Эффект зарегистрирован не был!
Ответ на вопрос о возможности порождения магнетизмом электричества искал и нашел его независимо от Фарадея американский физик Д. Генри. Но Генри запоздал с публикацией своих результатов и приоритет открытия явления, названного явлением электромагнитной индукции, принадлежит английскому физику М. Фарадею.
Фарадей проводил свои опыты на самодельных, весьма примитивных с нашей точки зрения и к тому же малочувствительных приборах.
Пронаблюдать эффекты, зарегистрированные Фарадеем, можно в несколько видоизмененном виде с помощью современных приборов.
Соберем установку, состоящую из соединенных между собой проволочной катушки и гальванометра, прибора служащего для обнаружения электрического тока в замкнутой цепи, для определения его величины и направления.
Будем вводить в катушку постоянный магнит северным полюсом. Стрелка гальванометра отклоняется вправо.
Когда магнит находится в состоянии покоя, стрелка гальванометра указывает на ноль.
При выведении магнита из катушки, стрелка гальванометра отклоняется влево.
Введем магнит в катушку южным полюсом, при этом
стрелка гальванометра отклоняется влево.
Когда магнит покоится, стрелка указывает на ноль.
При выведении магнита из катушки, стрелка гальванометра отклоняется вправо.
Изменим скорость движения магнита относительно катушки.
При медленном движении магнита относительно катушки, сила тока в цепи меньше, чем при быстром движении магнита.
Соберем установку, состоящую из двух не соединенных между собой цепей. Первая цепь состоит из последовательно соединенных источника постоянного тока, реостата, выключателя и проволочной катушки. Вторая цепь — индикаторная. Она состоит из гальванометра и другой проволочной катушки. Одна катушка находится внутри другой. Катушки неподвижны относительно друг друга.
При помощи реостата будем изменять силу тока в первой цепи.
Стрелка гальванометра отклоняется от нулевого деления, что указывает на наличие тока в индикаторной цепи.
При увеличении тока в первой цепи, стрелка гальванометра отклоняется в одну сторону, а при уменьшении — в другую.
Когда ток в первой цепи не меняется, стрелка гальванометра указывает на ноль.
Внесем внутрь второй катушки стальной сердечник.
При движении стального сердечника стрелка прибора отклонятся то вправо, то влево, в зависимости от направления его движения.
Если сердечник покоится относительно катушки, стрелка прибора не отклоняется.
Будем перемещать катушку с помещенным внутрь нее стальным сердечником относительно другой катушки.
Стрелка прибора отклоняется то вправо, то влево, в зависимости от направления движения катушки. При этом величина отклонения стрелки прибора значительно больше, чем в случае аналогичного движения катушки без сердечника.
Будем включать и выключать источник тока.
При включении источника тока, стрелка прибора отклоняется вправо от нулевого деления. При выключении источника тока, стрелка прибора отклоняется влево от нулевого деления.
Если по катушке протекает постоянный по величине и направлению электрический ток, стрелка электроизмерительного прибора, включенного в цепь другой катушки, не отклоняется от нулевого деления.
Подсоединим проволочную рамку к стрелочному электроизмерительному прибору.
При вращении рамки между полюсами постоянного магнита, электроизмерительный прибор показывает наличие изменяющегося по величине и направлению тока в цепи.
Если рамка покоится относительно магнита, тока в цепи нет.
Объединяет все опыты то обстоятельство, что в электрической цепи, не содержащей источника тока, образующей замкнутый контур, пронизываемый магнитным полем, наводится (индуцируется) электрический ток.
Чтобы отличать этот электрический ток от электрического тока, созданного источником, включенным в цепь, назовем его индукционным током.
В разных опытах индукционный ток появляется за счет разных причин, но везде эти причины связаны с магнитным полем, точнее с его изменением.
В одних случаях, различными способами изменяется индукция магнитного поля, пронизывающего контур, в других, меняется площадь контура, пронизываемого магнитным полем, или его ориентация относительно магнитного поля.
Чтобы легче было объединить причины возникновения индукционного тока, можно ввести физическую величину — магнитный поток (Ф).
Назовем магнитным потоком физическую величину, равную произведению модуля вектора индукции магнитного поля на площадь контура, пронизаваемого этим магнитным полем и на косинус угла между направлением вектора магнитной индукции и нормалью (перпендикуляром) к поверхности, ограниченной контуром
: .
На чертеже представление о величине магнитного потока можно отразить с помощью большего или меньшего числа магнитных силовых линий, пронизывающих тот или иной контур.
Чтобы получить единицу магнитного потока, надо в его определяющее уравнение подставить единицы магнитной индукции — 1 Тл и площади — 1 м2.
Получаем: [Ф] = 1 Тл 1 м2 .
Эта единица имеет собственное наименование — 1 Вб (вебер
).
При определении направления индуцируемых в замкнутом контуре электрических токов, сам Фарадей предлагал два различных правила для случая “вольта-электрической” и “магнитоэлектрической” индукции.
То, что в обоих случаях существует один и тот же индукционный процесс, подчиняющийся общему правилу, понял петербургский академик .
Чтобы сформулировать правило Ленца,
необходимо вновь вернуться к опытам по получению индукционных токов. Эти опыты можно провести, например, на такой установке:
На острие укреплено коромысло с двумя уравновешивающими друг друга кольцами, изготовленными из немагнитного металла (в данном случае — алюминия). Одно кольцо сплошное, другое — разрезанное.
Будем вдвигать и выдвигать в кольца постоянный магнит, меняя его полюса.
Движение магнита не оказывает никакого влияния на разрезанное кольцо.
При сближении магнита и сплошного кольца, кольцо отталкивается от магнита.
При удалении магнита от сплошного кольца, оно притягивается к магниту.
Результаты опытов не зависят от того, каким полюсом магнит обращен к кольцу.
Таким образом, обобщая результаты наблюдений, можно построить следующую цепочку суждений.
1. Раз кольцо начинает взаимодействовать с магнитом, значит вокруг него возникает магнитное поле.
2. Поскольку кольцо изготовлено из немагнитного металла, это поле может породиться протекающим по кольцу током.
3. Так как взаимодействие появляется только при взаимном движении кольца и магнита, ток в кольце появляется за счет этого движения.
4. При движении магнита относительно кольца изменяется магнитный поток, пронизывающий кольцо, следовательно, ток возникающий в кольце, является индукционным.
5. Так как при взаимном сближении кольца и магнита, происходит их отталкивание, вектор индукции магнитного поля магнита направлен противоположно вектору индукции магнитного поля кольца.
6. Так как при взаимном удалении кольца и магнита, происходит их притяжение, вектор индукции магнитного поля магнита сонаправлен с вектором магнитного поля кольца.
7. Во всех случаях, направление индукционного тока можно определить исходя из правила:
При изменении магнитного потока, пронизывающего замкнутый контур, в контуре возникает индукционный ток такого направления, что порожденное им магнитное поле создает магнитный поток препятствующий изменению магнитного потока, порождающего индукционный ток.
Конкретно, направление индукционного тока в проводнике и знак возникающей ЭДС можно определить следующим образом.
Рассмотрим случай, когда в проводящее кольцо вводится магнит. Магнитный поток, пронизывающий кольцо, нарастает. Вектор, индукции магнитного поля магнита, сонаправлен с вектором скорости движения магнита.
В этом случае вектор индукции магнитного поля, созданного индукционным током, направлен против скорости движения магнита.
Вращая правый винт так, чтобы направление вращения ручки совпадало с направлением силовых линий магнитного поля, созданного индукционным током (или, что то же самое, было противоположным направлению движения магнита), по направлению перемещения винта определяем направление индукционного тока. В нашем случае ток направлен против часовой стрелки.
| Из за большого объема этот материал размещен на нескольких страницах: 5 |
Взаимодействие токов
Рассмотрим два случая. Первый – ток течет по прямому проводу. Второй – по круговому витку. Как мы знаем, ток создает магнитное поле.
В первом случае магнитная индукция провода с током I на расстоянии R от него считается по формуле:
Мю – магнитная проницаемость вещества, мю с индексом ноль – магнитная постоянная.
Во втором случае магнитная индукция в центре кругового витка с током равна:
Также при решении задач может пригодиться формула для магнитного поля внутри соленоида. Соленоид – это катушка, то есть множество круговых витков с током.
Пусть их количество – N, а длина самого соленоилда – l. Тогда поле внутри соленоида вычисляется по формуле:
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Магнитный поток и ЭДС
Если магнитная индукция – векторная характеристика магнитного поля, то магнитный поток – скалярная величина, которая также является одной из самых важных характеристик поля. Представим, что у нас есть какая-то рамка или контур, имеющий определенную площадь. Магнитный поток показывает, какое количество силовых линий проходит через единицу площади, то есть характеризует интенсивность поля. Измеряется в Веберах (Вб) и обозначается Ф.
S – площадь контура, альфа – угол между нормалью (перпендикуляром) к плоскости контура и вектором В.
При изменении магнитного потока через контур в контуре индуцируется ЭДС, равная скорости изменения магнитного потока через контур. Кстати, подробнее о том, что такое электродвижущая сила, вы можете почитать в еще одной нашей статье.
По сути формула выше – это формула для закона электромагнитной индукции Фарадея. Напоминаем, что скорость изменения какой-либо величины есть не что иное, как ее производная по времени.
Для магнитного потока и ЭДС индукции также справедливо обратное. Изменение тока в контуре приводит к изменению магнитного поля и, соответственно, к изменению магнитного потока. При этом возникает ЭДС самоиндукции, которая препятствует изменению тока в контуре. Магнитный поток, который пронизывает контур с током, называется собственным магнитным потоком, пропорционален силе тока в контуре и вычисляется по формуле:
L – коэффициент пропорциональности, называемый индуктивностью, который измеряется в Генри (Гн). На индуктивность влияют форма контура и свойства среды. Для катушки с длиной l и с числом витков N индуктивность рассчитывается по формуле:
Формула для ЭДС самоиндукции:
Основные формулы раздела «Электромагнитная индукция»
Алгоритм решения задач по теме «Электромагнитная индукция»:
1. Внимательно прочитать условие задачи. Установить причины изменения магнитного потока, пронизывающего контур.
2. Записать формулу:
- закона электромагнитной индукции;
- ЭДС индукции в движущемся проводнике, если в задаче рассматривается поступательно движущийся проводник; если в задаче рассматривается электрическая цепь, содержащая источник тока, и возникающая на одном из участков ЭДС индукции, вызванная движением проводника в магнитном поле, то сначала нужно определить величину и направление ЭДС индукции. После этого задача решается по аналогии с задачами на расчет цепи постоянного тока с несколькими источниками.
3. Записать выражение для изменения магнитного потока и подставить в формулу закона электромагнитной индукции.
4. Записать математически все дополнительные условия (чаще всего это формулы закона Ома для полной цепи, силы Ампера или силы Лоренца, формулы кинематики и динамики).
5. Решить полученную систему уравнений относительно искомой величины.
6. Решение проверить.
Электромагнитные колебания и волны →
← Магнитное поле
Электромагнитная индукция
3.2 (64.8%) 50 votes
Энергия магнитного поля
Электроэнергия, ядерная энергия, кинетическая энергия. Магнитная энергия – одна из форм энергии. В физических задачах чаще всего нужно рассчитывать энергию магнитного поля катушки. Магнитная энергия катушки с током I и индуктивностью L равна:
Объемная плотность энергии поля:
Конечно, это не все основные формулы раздела физики «электричество и магнетизм», однако они часто могут помочь при решении стандартных задач и расчетах. Если же вам попалась задача со звездочкой, и вы никак не можете подобрать к ней ключ, упростите себе жизнь и обратитесь за решением в сервис студенческой помощи.