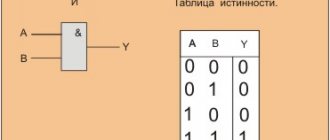
Обоснование векторной диаграммы
Предположим, что ток задан уравнением
i = Imsin(ωt +Ψ)
Проведем две взаимно перпендикулярные оси и из точки пересечения осей проведем вектор Im, длина которого в определённом масштабе Mi выражает амплитуду тока Im:
Im = Im/Mi
Направление вектора выберем так, чтобы с положительным направлением горизонтальной оси вектор составлял угол, равный начальной фазе Ψ (рис. 12.10).
Проекция этого вектора на вертикальную ось определяет мгновенный ток в начальный момент времени: i0 = ImsinΨ.
Представим себе, что вектор Im вращается против движения часовой стрелки с угловой скоростью, равной угловой частоте ω. Его положение в любой момент времени определяется углом ωt +Ψ ,
Тогда мгновенный ток для произвольного момента времени t можно определить проекцией вектора Im на вертикальную ось в этот момент времени.
Следующая статья сложение и вычитания векторов векторной диаграммы.
Например, для t = t1
i1 = Imsin(ωt1 +Ψ)
в общем случае
i = Imsin(ωt +Ψ)
Получили такое же уравнение, каким был задан переменный ток, что свидетельствует о возможности изображения тока вращающимся вектором при нанесении его на чертеж в начальном положении.
Переменный ток. Векторные диаграммы
Переменным током называется ток, который с течением времени изменяется и по величине, и по направлению. В электротехнике в основном используется синусоидальный переменный ток, т.е. изменяющийся с течением времени по закону синуса. Математически мгновенное значение синусоидального тока выражается следующим образом:
, (2.1)
где i
– мгновенное значение тока в момент времени
t
,
Im
– максимальное (амплитудное) значение тока,
ω
– круговая (угловая) частота. Угловая частота
ω
связана с частотой
f
переменного тока выражением . Выражение
ω t
называется фазой колебаний или фазовым углом. Фазой характеризуется состояние процесса изменения тока в данный момент времени
t
.
График синусоидального тока представлен на рис. 2.1а. По оси ординат отложено мгновенное значение тока, по оси абсцисс – фазовый угол в градусах или радианах. На оси абсцисс можно откладывать и непосредственно время t
, а не величину
ω t
, причем время удобно измерять в долях периода
T
.
Рис. 2.1. Изображение графика синусоидального тока (а)
и векторной диаграммы (б)
Кроме графического и тригонометрического представления синусоидального тока имеется еще метод вращающегося радиус вектора (рис. 2.1 б). При анализе параметров переменного тока этот метод в ряде случаев облегчает вывод некоторых формул, а также является очень наглядным при качественном рассмотрении процессов, происходящих в цепях переменного тока. Представим максимальный ток Im
в виде вектора
I в некотором произвольном масштабе. Теперь предположим, что этот вектор вращается вокруг своего начала – точки 0 против часовой стрелки с угловой скоростью ω
равной угловой частоте
ω
.
Пусть в момент времени t = 0
вектор
I совпадает по направлению с осью OX, (начальной осью). Тогда к моменту времени t = t 1
вектор повернется на угол
ω t 1
по отношению к начальной оси. Проекция вектора
I в этом положении на вертикальную ось равна отрезку OA:
. (2.2)
Сравнивая формулы (2.1) и (2.2) можно увидеть, что отрезок OA в выбранном масштабе дает мгновенное значение тока в момент времени t = t 1
, если в момент времени
t = 0
мгновенное значение этого синусоидального тока равнялось нулю (проекция вектора
I на вертикальную ось в начальный момент t = 0
). Таким образом, мы можем считать, что проекция вращающегося радиус вектора
I на вертикальную ось в любой момент времени представляет в определенном масштабе мгновенное значение тока в этот момент. Точно также можно построить развернутую графическую зависимость этой величины от времени. На рис. 2.2 изображен вектор I, представляющий переменную величину и соответствующая развернутая векторная диаграмма для i
.
Рис. 2.2. Графическое и векторное представление синусоидального тока
Если в начальный момент времени t = 0
вектор
I составляет с начальной осью некоторый угол, то развернутая диаграмма для этого случая представлена на рис. 2.3 а и 2.3 б. Мгновенное значение тока в зависимости от времени в этих случаях записывается следующим образом: для рис. 2.3 а, и для рис. 2.3 б. Угол, определяющий положение вектора I в момент времени t = 0
, называется начальной фазой.
Рис. 2.3 Графическое и векторное представление вектора I
для двух начальных фаз
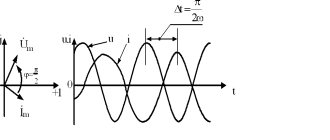
Если две периодические величины в своих измерениях одновременно проходят нулевые и максимальные значения, одновременно возрастают и убывают, то об этих величинах можно сказать, что они совпадают по фазе. На рис. 2.4 показаны кривые: тока и напряжения, совпадающие по фазе, полученные вращением двух векторов U и I, совпадающих по направлению и имеющих начальную фазу равную 0. На рис. 2.5 изображены две величины U
и
I
, имеющие различные начальные фазы.
Рис. 2.4. Тригонометрическое изображение и векторная диаграмма
для случая совпадения напряжения и тока по фазе
Разность начальных фаз φ = α – β
называется сдвигом фаз. На рис. 2.5 видно, что кривая тока опережает по фазе кривую напряжения, т.к. она раньше по времени достигает своего максимального значения, раньше начинает убывать и т.д. Стоит отметить, что при вращении этих двух векторов угол между ними не изменяется.
Рис. 2.5. Изображение величин U
и
I
, имеющих различные
начальные фазы в векторном и графическом виде
При одновременном действии двух или нескольких переменных однородных величин (в частности, двух токов или двух напряжений) происходит сложение мгновенных значений этих величин. Результат такого сложения можно изобразить графически, если построить две синусоиды, и в каждый момент времени сложить ординаты этих синусоид и по сумме ординат построить третью синусоиду. Вместе с тем, гораздо проще и нагляднее пользоваться методом геометрического сложения радиус-векторов, представляющих соответствующие величины. При этом возможно определить не только амплитудное значение, но и начальную фазу. На рис. 2.6 показано сложение двух токов I 1
и
I 2
с различными амплитудными значениями и различными фазами.
Рис. 2.6. Сложение двух синусоидальных токов векторным
и графическим способами
Стоит отметить, что, как правило, важно знать не мгновенное значение тока или напряжения, а иметь возможность оценить действие переменного тока в течение некоторого промежутка времени, т.е. знать некоторое усредненное значение переменного тока или напряжения. В зависимости от вида действия тока (химическое, тепловое, электродинамическое и т.д.) следует пользоваться различными усреднениями. Например, для оценки химического действия следует брать среднее арифметическое значение переменного тока за определенный промежуток времени. Для синусоидального переменного тока данное значение равно нулю за период. Поэтому использование переменного тока для процесса электролиза не годится. В свою очередь, тепловое и электродинамическое действие тока пропорционально квадрату силы тока и. следовательно, в этих случаях представляет собой интерес среднеквадратичное значение переменного тока. Вычислим среднеквадратичное значение тока на примере теплового действия тока. В случае переменного тока в веществе за бесконечно малый промежуток времени dt
выделится количество теплоты
dQ
, т.е.: , где
i
– мгновенное значение переменного тока в течении времени
dt .
Количество теплоты за промежуток времени
T
равно:
. (2.3)
Далее найдем значение постоянного тока I
за такой же промежуток времени
T
, при котором выделится эквивалентное количество теплоты
Q .
Так как , то . Теперь подставим вместо
Q
выражение (2.3): . Значение переменного тока, которое действует аналогично значению постоянного тока, называется действующим значением переменного тока. Математически данное предложение можно записать следующим образом:
. (2.4)
Из последнего выражения видно, что действующее значение тока I
равно среднеквадратичному значению переменного тока.
Получим соотношение между действующим значением тока I и амплитудным значением тока Im для переменного синусоидального тока . Для этого следует определить значение интеграла:
.
Видно, что: первый интеграл: , второй интеграл — . Следовательно, для случая синусоидального тока можно записать:
. (2.5)
Аналогичным образом выглядит соотношение между действующим и амплитудным значениями переменного напряжения:
. (2.6)
Стоит отметить, что электроизмерительные приборы (амперметры и вольтметры) электромагнитной, электродинамической и некоторых других систем показывает среднеквадратичное значение тока и напряжения, и следовательно, действующее значение этих величин. В свою очередь, приборы магнитоэлектрической системы показывают среднеарифметическое ли просто среднее значение переменного тока. По этой причине приборы данной системы не пригодны для измерений параметров переменного тока.
Рассмотрим теперь электрические цепи, содержащие различные типы нагрузки, в частности активное сопротивление (резистор), индуктивное сопротивление (катушка индуктивности), емкостное сопротивление (конденсатор).
1) Цепь переменного тока, содержащая активное сопротивление
.
Пусть к активному сопротивлению R
приложено переменное напряжение . Тогда в цепи пойдет переменный ток
i
такой же частоты, но по фазе ток, вообще говоря, может не совпадать по фазе с напряжением, т.е. выражение для мгновенного значения тока имеет вид:
. (2.7)
Для бесконечно малых промежутков времени мы вправе применить к переменному току закон Ома, справедливый для постоянного тока, считая, что токи и напряжения в эти малые промежутки времени не изменятся. Для мгновенных значений тока и напряжения можно записать:
. (2.8)
Заменяя U
в выражении (2.8) через получим:
. (2.9)
Сравнивая выражения (2.7) и (2.9) можно увидеть, что , а φ
= 0. Следовательно, фазы тока и напряжения одинаковы, разность фаз равна нулю, т.е. ток и напряжение совпадают по фазе. Электрическая цепь и векторная диаграмма для нее изображена на рис. 2.7.
Рис.2.7. Электрическая цепь, содержащая активное сопротивление (а),
и векторная диаграмма к ней (б)
2) Цепь переменного тока, содержащая индуктивное сопротивление.
На рис. 2.8 изображена цепь переменного тока, содержащая катушку индуктивности. Для простоты рассуждений будем считать данную катушку индуктивности идеальной, т.е. ее активное сопротивление равно нулю. На практике, особенно в области высоких частот, такое допущение корректно.
Рис. 2.8. Цепь переменного тока, содержащая катушку индуктивности
Приложим к данной катушке переменное напряжение . В этом случае по катушке пойдет переменный ток, который своим магнитным полем будет наводить в катушке переменную ЭДС самоиндукции E
. По закону Кирхгофа для мгновенных значений переменного тока имеем , но т.к.
R
= 0, то
U = — E
. В свою очередь, из закона электромагнитной индукции известно, что:
, (2.10)
где L
– коэффициент самоиндукции катушки, или просто индуктивность. Т.к. ток по фазе может не совпадать с напряжением, представим его в виде:
, (2.11)
где φ
– сдвиг фаз между током и напряжением. Подставив (2.11) в (2.10), и продифференцировав, можно получить:
. (2.12)
Сравнив (2.9) и (2.12), можно записать:
. (2.13)
Отсюда можно сделать следующие выводы:
а) . Так как величина ωL
имеет такую же размерность, что и сопротивление, по аналогии с законом Ома
U = IR
для активного сопротивления можно считать произведение
ωL
индуктивным сопротивлением катушки. Наличие индуктивного сопротивления цепи обусловлено противодействием ЭДС самоиндукции E переменному току, протекающему в цепи согласно правилу Ленца. Индуктивное сопротивление, также как и ЭДС самоиндукции, зависит от индуктивности цепи и скорости изменения тока, которая в случае переменного тока определяется частотой тока.
б) , если φ =
-90º. Следовательно, в выражении для тока (2.11) угол
φ
следует заменить на угол 90º. Таким образом можно записать:
(2.14)
Из данного выражения можно сделать вывод о том, что ток в катушке индуктивности отстает по фазе по фазе от напряжения, приложенного к катушке, на угол 90º. На рис. 2.9 изображен графический и векторный вид тока и напряжения для случая идеальной катушки индуктивности.
Рис. 2.9. Векторное и графическое представление тока и напряжения
цепи переменного тока, содержащей индуктивное сопротивление
Вместе с тем, в некоторых случаях считать активное сопротивление R
катушки равным нулю нельзя. В этом случае катушку индуктивности рассматривают в виде последовательного соединения активного сопротивления
R
и чистой индуктивности
L
без активного сопротивления и анализируют получившуюся RL цепь (рис. 2.10).
Соотношения, полученные для амплитудных значений тока Im
и напряжения
Um
также справедливы и для действующих значений тока
I
и напряжения
U
. В частности, если разделить обе части равенства на √2, то получится соотношение . Аналогично можно получить выражение для активного сопротивления, т.е. . Поэтому если по цепи (рис. 2.10) идет ток
I
, то напряжение на активном сопротивлении равно
Ua = IR
, а на индуктивном
UL = IXL
.
Рис. 2.10. Электрическая цепь, иллюстрирующая катушку индуктивности
с ненулевым активным сопротивлением
Построим векторную диаграмму напряжений для данной цепи, но вместо амплитудных значений будем использовать действующие значения напряжения, что эквивалентно изменению масштаба отрезков в √2 раза. Отложим вектор Ua = IR
в направлении тока
I
, а вектор
UL
, направленным относительно I на 90º против часовой стрелки (рис. 2.11). Общее напряжение равно векторной сумме напряжений
Ua
и
UL
.
Рис. 2.11. Векторное и графическое представление напряжений
в RL цепи
Воспользовавшись правилом сложения векторов, выражение для общего напряжения можно записать в следующем виде:
(2.15)
Из данного выражения видно, что сдвиг фаз между общим напряжением и током зависит от соотношения Ua
и
UL
, и, следовательно, и от соотношения
R
и
XL
. Из рис. 2.11 видно, что . Разделив полное выражение на величину тока
I
, можно найти полное сопротивление
Zk
катушки, равное:
(2.16)
В свою очередь, для сдвига фаз можно записать следующее выражение:
(2.17)
3) Цепь переменного тока, содержащая конденсатор.
Если обкладки конденсатора присоединить к источнику постоянного тока, то ток в цепи будет идти до тех пор, пока на обкладках конденсатора за счет протекающего заряда не возникает разность потенциалов равная ЭДС источника. Если же на конденсатор подать переменное напряжение, то конденсатор будет непрерывно перезаряжаться, и в цепи все время будет идти переменный ток, при этом, чем больше емкость конденсатора, тем больший ток будет течь по цепи (рис. 2.12, 2.13).
Рис. 2.12. Цепь переменного тока, содержащая конденсатор
Рис. 2.13. Векторное и графическое представление тока и напряжения
в цепи, содержащей конденсатор
Пусть к конденсатору приложено переменное напряжение , в этом случае заряд конденсатора будет меняться со временем так же, как меняется напряжение на нем. Если C
– емкость конденсатора, то . За бесконечно малый промежуток времени
dt
заряд изменяется на величину
dq
. Зная определение силы тока, можно записать: . Приняв , можно записать: . Так как имеет размерность сопротивления, поэтому ее обозначают и называют емкостным сопротивлением. Из формул для тока и напряжения видно, что ток опережает напряжение на 90°.
Рассмотрим теперь цепь переменного тока, состоящую из последовательно соединенных сопротивления R
, конденсатора
C
и идеальной катушки индуктивности
L
(рис. 2.14). Так как элементы в цепи соединены последовательно, то по всем элементам цепи протекает один и тот же ток
I
. Следовательно, напряжение на элементах цепи определяется по закону Ома для участка цепи: , , .
Рис. 2.14. Цепь переменного тока, содержащая в себе последовательно соединенные резистор, конденсатор и катушку индуктивности
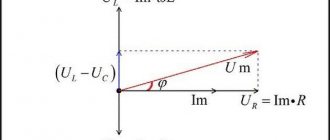
Построим векторную диаграмму для такой цепи. Начальную фазу тока примем равной 0, т.е. вектор I направим вдоль начальной оси. Напряжение Ua следует отложить в этом же направлении, т.к. ток и напряжение на активном сопротивлении совпадают по фазе. Напряжение на катушке индуктивности UL будет опережать ток на 90º, а напряжение на конденсаторе UC будет отставать от тока на 90º. Треугольник напряжений для цепи (2.14) изображен на рис. 2.15.
Рис. 2.15. Векторная диаграмма для цепи, в которой последовательно
соединены сопротивление, конденсатор и катушка индуктивности
Общее напряжение цепи равно геометрической сумме напряжений на отдельных участках. Для того, чтобы его найти необходимо сначала сложить противоположные вектора UL и UC, а затем к получившемуся вектору прибавить вектор Ua. Векторная сумма UL+UC равна алгебраической разности модулей векторов UL
и
UC
, т.е.
( UL — UC )
. Тогда:
. (2.18)
Подставив в (2.18) вместо Ua
,
UL
и
UC
их выражения через ток
I
и соответствующие сопротивления можно получить:
.
Обозначим выражение через Z:
. (2.19)
Величина Z
называется полным сопротивлением цепи. Из данного выражения видно, что полное сопротивление цепи вычисляется через
R
,
XL
,
XC
аналогично тому, как вычисляется общее напряжение всей цепи через напряжения на компонентах цепи. По аналогии с рис. 2.15 можно построить треугольник сопротивлений (рис. 2.16).
Рис. 2.16. Треугольник сопротивлений для полной цепи
переменного тока
Сдвиг фаз φ
между током
I
и общим напряжением
U
определяется из соотношений:
; , (2.20)
Знак сдвига фаз φ
зависит от преобладания в цепи индуктивной или емкостной нагрузки.
Рассмотрим случай, когда индуктивное сопротивление равно емкостному в цепи переменного тока, т.е. . Тогда . Следовательно, и φ =
0, т.е. сдвига фаз между током и напряжением нет, а полное сопротивление
Z = R
. В этом случае говорят о наличии резонанса напряжений в цепи. Явление резонанса используется в радиотехнике для выделения сигнала определенной радиостанции. В свою очередь, в электротехнике, как правило, резонанс напряжений – явление опасное, т.к. оно связано с возникновением перенапряжений на элементах цепи, в разы превышающих рабочее напряжение установки. При этом плавкие и подобные предохранители не способны осуществить защиту установки от этих перенапряжений. Рассмотрим пример. Имеется цепь переменного тока, в которой соединены последовательно активное сопротивление
R =
10 Ом и реактивные сопротивления
XL = XC =
1000 Ом. Приложенное напряжение возьмем равное
U =
100 В. Тогда ток в цепи . Тогда напряжения на катушке индуктивности и на конденсаторе будут соответственно равны
UL = IXL =
10
А ·
1000
О
=10000
В
и
UC = IXC =
10
А ·
1000
Ом
=10000
В
. Видно, что напряжения на элементах цепи во много раз превышают напряжение источника. Если изоляция в конденсаторе и/или катушке индуктивности не рассчитаны на такое напряжение, то данные элементы цепи выйдут из строя.
В общем случае величина напряжения на катушке индуктивности или на конденсаторе при резонансе во столько раз превышают напряжение, подводимое ко всей цепи, во сколько раз реактивные сопротивления XL
и
XC
больше активного сопротивления
R
:
; . (2.21)
Таким образом, перенапряжение при резонансе возникает при R < XL
и
R < XC
. Поскольку резонанс возникает при условии , то легко можно получить выражение для резонансной частоты, а именно:
. (2.22)
Подставляя (2.22) в выражение XL
и
XC
, можно получить общее условие возникновения перенапряжения при резонансе:
; ; . (2.23)
Величина не зависит от частоты и является собственной характеристикой контура. Так как данная величина имеет размерность сопротивления, ее называют характеристическим или волновым сопротивлением контура ρ
.
Стоит отметить, что напряжение на конденсаторе UC
и катушке индуктивности
UL
не всегда будут максимальными при резонансе. Добиться явления резонанса в цепи можно с помощью подбора либо частоты
ω
, либо емкости конденсатора
C
, либо индуктивности катушки
L
. График зависимости
UC
и
UL
от частоты приведен на рис. 2.17. Из данного рисунка видно, что напряжение
UC
и
UL
достигают при разных частотах
ω C
и
ω L
. Одна из них меньше, а другая больше резонансной частоты
ω0
. Чем меньше активное сопротивление контура, тем максимумы
UL
и
UC
выше и ближе друг к другу. Совпадают же они при
R = 0
, и, наоборот, при достаточно большом сопротивлении
R
(
R >ρ
) зависимости
UC (ω)
и
UL (ω)
не имеют максимумов.
Рис. 2.17. Частотные зависимости UC
,
UL
и
I
Рис. 2.18. Емкостные зависимости UC
,
UL
и
I
В данной лабораторной работе настройка цепи на резонанс осуществляется изменением емкости C
. Зависимости
UC ( C )
и
UL ( C )
приведены на рис. 2.18. При резонансной емкости напряжение на катушке индуктивности достигает максимума. В свою очередь, напряжение на конденсаторе
UC
достигает максимума при емкости меньшей, чем
C рез
.
При практическом осуществлении режима резонанса напряжений следует учитывать наличие активного сопротивления у катушки индуктивности. Вольтметр, подключенный к катушке, показывает полное напряжение на ней, которое соответствует . Данное напряжение при резонансе не равно напряжению на конденсаторе UC
. Следовательно, настройка на резонанс осуществляется по максимуму тока
I
.
Рассмотрим теперь мощность, выделяемую в цепи переменного тока. Так как ток и напряжение меняются, то, соответственно, и мощность в цепи переменного тока есть величина переменная, и, следовательно, можно говорить только о мгновенной мощности p
, определяемой произведением мгновенного значения тока на мгновенное значение напряжения, т.е.
p = i · u
. В общем случае, когда разность фаз между током и напряжением равна
φ
, мгновенная мощность
p
будет определяться следующим выражением:
. (2.24)
Применив ряд тригонометрических преобразований, можно получить:
. (2.25)
Заменив амплитудные значения тока и напряжения на действующие, получим:
. (2.26)
Последнее выражение постоянную составляющую и гармоническую составляющую , изменяющуюся с двойной частотой 2ω t
. В случае активной нагрузки (
φ =
0, cos
φ =
1) мгновенная мощность определяется выражением . В случае чисто индуктивной нагрузки (
φ =
90°, cos
φ =
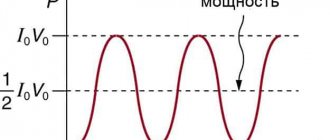
0) мгновенная мощность определяется выражением . В случае чисто емкостной нагрузки выражение для мгновенной мощности отличается от предыдущего только знаком, т.е. . Наличие этого знака ярко проявляется при резонансе. Графики для мгновенных мощностей для случая активной, индуктивной и емкостной нагрузок изображены на рис. 2.19 (а, б, в).
Рис. 2.19 а. Частотная зависимость мгновенной мощности
в случае активной нагрузки
Рис. 2.19 б. Частотная зависимость мгновенной мощности
в случае индуктивной нагрузки
Рис. 2.19 в. Частотная зависимость мгновенной мощности
в случае емкостной нагрузки
На практике представляет интерес не мгновенное значение мощности, а ее среднее значение за большой промежуток времени, соответствующий большому количеству периодов колебаний мощности. Эту мощность можно измерить с помощью ваттметра. Так как стрелка ваттметра не успевает отслеживать мгновенные значения мощности, то она устанавливается в положении, соответствующем некоторому среднему значению мощности. Определим эту величину. Работа переменного тока dA
за малый промежуток времени
dt
равна . В свою очередь, работа за период равна , средняя мощность p за это же время равна . Далее, учитывая формулу (2.26), можно записать:
,
или же
.
Второй интеграл равен нулю, т.к. интеграл от функции косинус за целый период равен нулю. Следовательно, средняя мощность имеет вид:
, (2.27)
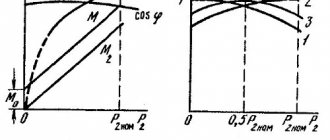
т.е. определяется не только действующими значениями тока и напряжения на потребителе, но и сдвигом фаз φ
между током и напряжением. Величину cos
φ
называют коэффициентом мощности, и она играет существенную роль среди параметров, характеризующих потребителя. Чем меньше cos
φ
, тем менее эффективно используется мощность, подводимая от генератора к потребителю и тем больше потери энергии в подводимых проводах.
Так как в общем случае , то выражение для средней мощности можно записать в виде . Далее, заменив отношение действующего напряжения к полному сопротивлению через ток , имеем . Таким образом, средняя мощность в цепи переменного тока равна мощности, выделяемой на активном сопротивлении R
цепи.
Активная мощность P
является основной величиной, характеризующей энергетические процессы в цепях переменного тока, но не единственной. Например, в случае чисто индуктивной нагрузки активная мощность равна нулю. Однако при этом по подводящим проводам течет переменный ток и между генератором и потребителем происходит обмен энергией (знаки + и – на рис. 2.19 б.) Интенсивность этого обмена зависит от действующих значений тока
I
и напряжения
U
и определяется реактивной мощностью
Q
. Аналогичный обмен энергией происходит и при чисто емкостной нагрузке (рис. 2.19 в). По этой причине индуктивную и емкостную нагрузки, обобщая, называют реактивными. В случае смешанной нагрузки, например, активно-индуктивной, реактивная мощность определяется выражением . Поскольку при этом энергетические процессы в цепи будут определяться как активной мощностью
P
, так и реактивной мощностью
Q
, то было введено понятие полной мощности
S
. Полная мощность в цепи при любом характере нагрузки равна произведению действующего значения тока и действующего значения напряжения, т.е. .Используя векторную диаграмму напряжений для какой-либо нагрузки, можно получить соотношение между полной, активной и реактивной мощностями для этой нагрузки. Для этого стороны векторной диаграммы напряжений умножаем на ток и получаем треугольник мощностей (рис. 2.20). Из данного треугольника можно записать следующее выражение для полной мощности: . Единицей измерения активной мощности является ватт (Вт) или киловатт (кВт), реактивной мощности – вольт-ампер реактивный (Вар) или киловольт-ампер реактивный (кВар), полной мощности – вольт-ампер (Ва) или киловольт-ампер (кВа). Такое различие в наименовании, кроме численного значения мощности, показывает, о какой именно мощности идет речь.
Рис. 2.20. Треугольник мощностей цепи переменного тока
Практическая часть
Задание I: Исследование неразветвленной цепи переменного тока.
1) Собрать электрическую схему, изображенную на рис. 2.21.
Приборы и компоненты:
ваттметр с пределами измерений по току 1 – 2 А, амперметр с пределами измерений 0.25 – 1 А, два вольтметра с пределами измерений 75 В (второй вольтметр используется для измерений напряжений на различных участках цепи), катушка однофазного трансформатора на 220 В или катушка индуктивности на 1200 витков (сердечник катушки разомкнут), магазин конденсаторов. К магазину конденсаторов следует подключить параллельно конденсатор постоянной емкости в 10 мкФ.
Примечание:
Для удобства измерений второй вольтметр следует подключить параллельно вольтовой обмотке ваттметра и затем с данного вольтметра вывести свободные проводники для возможности подключения данной измерительной системы к различным участкам цепи.
Рис. 2.21. Рабочая электрическая схема для выполнения задания I
Таблица 2.1
| Режим | Участок цепи | Измерить | Вычислить | ||||||||
| I,А | U,В | P, Вт | Z, Ом | R, Ом | XL,Ом | XC,Ом | S, Ва | Q, Вар | cosφ | ||
| XL > XC C = 40 мкФ | R | ||||||||||
| L | |||||||||||
| C | |||||||||||
| R + L +C | |||||||||||
| XL = XC C ≈ 20мкФ | R | ||||||||||
| L | |||||||||||
| C | |||||||||||
| R + L + C | |||||||||||
| XL < XC C = 10 мкФ | R | ||||||||||
| L | |||||||||||
| C | |||||||||||
| R + L + C | |||||||||||
2) Для трех разных значений емкости конденсатора (см. таблицу 2.1) произвести измерения тока, напряжения и активной мощности (ваттметр измеряет активную мощность) на активном сопротивлении (R1 + R3), на индуктивном сопротивлении L, емкостном сопротивлении C, а также на всем участке цепи, т.е. R + L + C. Напряжение источника следует выставить порядка 70 В. Получившиеся данные занести в таблицу 2.1.
Примечание:
В опыте 2 (
XL = XC
) добиться резонанса напряжений, ориентируясь по наибольшему току в цепи.
3) Произвести расчеты согласно таблице 2.1.
4) Построить в масштабе векторные диаграммы напряжений, треугольники сопротивлений и мощностей для всех трех опытов с учетом того, что вольтметр, подключенный к катушке индуктивности, показывает полное напряжение на этом участке, а не чисто индуктивную составляющую.
Задание II: Исследование явления резонанса напряжений.
1) Собрать схему, изображенную на рис. 2.22.
Примечание:
Слева на указанной схеме изображен трехфазный трансформатор. В данной схеме обмотки данного трансформатора подключаются звездой, т.е. на начала первичной обмотки (A, B, C) подается трехфазное напряжение (с клемм A, B, C) со стенда, концы первичной обмотки X, Y, Z соединяются между собой, концы вторичной обмотки x, y, z также соединяются между собой, с клемм a, b, c снимается трехфазное напряжение. При выполнении данного задания в качестве источника напряжения используются две любые из этих клемм.
Рис. 2.22. Рабочая электрическая схема для выполнения задания II
Приборы и компоненты:
амперметр с пределами измерений 0.25 – 1 А, вольтметр V1 с пределами измерений до 60 В (использовать 15 В), два вольтметра (V2 и V3) с пределами измерений 75 В, катушка однофазного трансформатора на 220 В или катушка индуктивности на 1200 витков (сердечник катушки разомкнут), магазин конденсаторов.
2) Произвести расчеты, согласно таблице 2.2.
Таблица 2.2
| Измерить | Вычислить | |||||||||
| C, мкФ | U, В | UL, В | UC, В | I, А | Z, Ом | Zk, Ом | XL, Ом | XC, Ом | S, Ва | cosφ |
| 10 | ||||||||||
| 12 | ||||||||||
| 14 | ||||||||||
| 15 | ||||||||||
| 16 | ||||||||||
| 17 | ||||||||||
| 18 | ||||||||||
| 19 | ||||||||||
| 20 | ||||||||||
| 21 | ||||||||||
| 22 | ||||||||||
| 23 | ||||||||||
| 24 | ||||||||||
| 26 | ||||||||||
| 28 | ||||||||||
| 30 | ||||||||||
| 32 | ||||||||||
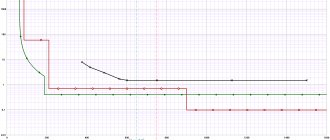
3) По данным измерений и расчетов построить на общем рисунке графики зависимостей: I = f ( C )
,
UC = f ( C )
,
UL = f ( C )
,
Z = f ( C )
, cos
φ = f ( C )
.
Контрольные вопросы
1) Какими параметрами характеризуется синусоидальный ток и напряжение?
2) Какова связь между синусоидально изменяющейся величиной и вектором x, ее представляющим? Как осуществить переход от синусоидальной кривой к векторной диаграмме и наоборот?
3) Что называется среднеквадратичным (действующим) значением синусоидального тока?
4) Каково соотношение между амплитудным и амплитудным значением тока?
5) Какое значение тока (мгновенное, амплитудное, среднее, действующее) показывает амперметр, включенный в цепь переменного тока?
6) Почему сопротивление катушки в цепи переменного тока больше ее сопротивления в цепи постоянного тока?
7) Раскройте физический смысл активного сопротивления.
9) Раскройте физический смысл емкостного сопротивления.
10) Покажите, что средняя мощность в цепи переменного тока равна активной мощности.
11) Что такое активная, реактивная и полная мощности в цепи переменного тока? Каковы единицы измерения этих величин?
12) Что такое резонанс напряжений?
13) Почему при резонансе напряжений на зажимах катушки индуктивности и конденсатора напряжение может быть больше напряжения, приложенного ко всей цепи?
14) Докажите, что максимум кривой UC ( C )
лежит левее максимума кривой
UL ( C )
.
15) Докажите, что максимум кривой UC ( ω )
лежит левее максимума кривой
UL ( ω )
.
16) Нарушится ли резонанс напряжений в цепи, если в эту цепь дополнительно включить активное сопротивление?
а) Последовательно с XC
и
XL
.
б) Параллельно XC
и
XL
.
в) Параллельно XC
или
XL
.
Построение векторной диаграммы
Вращая вектор Im‘ против движения часовой стрелки, в прямоугольной системе координат построим график изменения проекции его на вертикальную ось в пределах одного оборота (одного периода). Получим известный уже график синусоидальной функции, соответствующий заданному уравнению.
При построении векторов положительные углы отсчитывают от положительного направления горизонтальной оси против вращения часовой стрелки, а отрицательные — по ее движению.
В процессе расчета электрической цепи определяется ряд синусоидальных величин. Все их можно изобразить на одном чертеже при помощи вращающихся векторов, привязав к одной паре взаимно перпендикулярных осей.
Совокупность векторов, изображающих на одном чертеже несколько синусоидальных величин одинаковой частоты в начальный момент времени, называется векторной диаграммой.
Например, напряжение и ток в электрической цепи выражаются уравнениями:
u = 125 sin(ωt + 30°)
i = 12 sin(ωt — 20°).
Векторная диаграмма такой цепи изображена на рис. 12.11. Если выбрать масштабы напряжения и тока
Mu = 50 В/см; Mi = 4 А/см;
то
Um = Um/Mu = 125/50 = 2,5 см; Im = Im = im/Mi = 12/4 = 3 см.
Векторная диаграмма содержит векторы синусоидальных величин одинаковой частоты, поэтому они вращаются с одинаковой частотой и их взаимное расположение не меняется.
Начало отсчета времени выбирают произвольно, поэтому один из векторов диаграммы можно направить произвольно; остальные же нужно располагать с учетом сдвига фаз по отношению к первому или предыдущему вектору.
Разновидности векторных диаграмм и правила их построения
Определение 1
Векторная диаграмма – это совокупность векторов на комплексной прямой, которая соответствует комплексным параметрами и/или величинам электрической цепи.
Векторные диаграммы могут быть:
- Точеными.
- Качественными.
Построение точечных диаграмм осуществляется с соблюдением масштаба всех величин согласно результатам численного анализа. Основное назначение точечных диаграмм — проверка результатов расчета. Качественные векторные диаграммы строятся с учетом взаимосвязей между комплексными величинами. Построение данного вида диаграмм, как правило, заменяет расчет, или предшествует ему. В качественных векторных диаграммах значения параметров (или величин) и масштаб изображения несущественны. Основное требование к ним заключается в том, чтобы все связи между величинами были отображены корректно. Этот вид диаграмм является одним из основных инструментов анализа цепей переменного тока.
Ты эксперт в этой предметной области? Предлагаем стать автором Справочника Условия работы
Векторные диаграммы делятся на круговые и линейные. В круговой векторной диаграмме геометрическим местом точек перемещения конца вектора является окружность или полуокружность. В линейных векторных диаграммах геометрическим местом точек конца вектора является прямая линия.
Перед построением векторной диаграммы сначала вычерчивается и анализируется схема замещения, которая эквивалентна принципиальной схеме электрической цепи. На данной схеме обязательно отмечаются каждый элемент электрической цепи, наносятся направления всех напряжений и токов. Векторные диаграммы токов и напряжений должны чертиться в крупных масштабах, выбор которого осуществляется по самой большой вычисленной или измеренной величине электрического тока или напряжения.
Несимметричные режимы в простейших характерных случаях (короткое замыкание и холостой ход) могут быть проанализированы на основе построения векторных диаграмм.
Рассмотрим режимы обрыва и короткого замыкания фазы при соединении в звезду для трех- и четырехпроводной систем. При этом будем проводить сопоставление с симметричным режимом работы цепи, фазные напряжения и токи в которой будут базовыми. Для этой цепи (см. рис.1,а) векторная диаграмма токов и напряжений приведена на рис. 1,б (принято, что нагрузка носит активно-индуктивный характер). Здесь
При обрыве фазы А нагрузки приходим к векторной диаграмме на рис. 2.
В этом случае
.
При коротком замыкании фазы А (трехпроводная система) имеет место векторная диаграмма на рис. 3. Из нее вытекает: ; ; ; ; .
При обрыве фазы А в четырехпроводной системе (нейтральный провод на рис. 1,а показан пунктиром, а вектор тока — пунктиром на рис. 1,б) ; ; .
Симметричный трехфазный приемник при соединении в треугольник и соответствующая этому случаю векторная диаграмма напряжений и токов приведены на рис. 4.
Здесь при том же способе соединения фаз генератора ; ; ; ; ; .
При обрыве провода в фазе А-В нагрузки, как это видно из схемы на рис. 5, ; , при этом сами токи и в силу автономности режима работы фаз при соединении нагрузки в треугольник такие же, как и в цепи на рис. 4,а. Таким образом, ; ; .
Цепь при обрыве линейного провода А-А’ и соответствующая этому случаю векторная диаграмма приведены на рис.6.
Здесь
; ; .
Мощность в трехфазных цепях
Мгновенная мощность трехфазного источника энергии равна сумме мгновенных мощностей его фаз:
.
Активная мощность генератора, определяемая как среднее за период значение мгновенной мощности, равна
.
Соответственно активная мощность трехфазного приемника с учетом потерь в сопротивлении нейтрального провода
,
реактивная
и полная
.
Суммарная активная мощность симметричной трехфазной системы
| . | (1) |
Учитывая, что в симметричном режиме для звезды имеют место соотношения
и для треугольника —
на основании (1) для обоих способов соединения фаз получаем
,
где j — угол сдвига между фазными напряжением и током.
Аналогично
Докажем теперь указанное ранее свойство уравновешенности двухфазной системы Тесла и симметричной трехфазной системы.
1. Двухфазная система Тесла
В соответствии с рис. 7
| (2) |
| . | (3) |
С учетом (2) и (3)
.
Таким образом, суммарная мгновенная мощность фаз есть величина постоянная, равная суммарной активной мощности источника.
2. Симметричная трехфазная цепь
Тогда
Отсюда
,
т.е. и для симметричной трехфазной цепи свойство уравновешенности доказано.
Измерение мощности в трехфазных цепях
Ниже рассмотрены практические схемы включения ваттметров для измерения мощности в трехфазных цепях.
1. Четырехпроводная система, несимметричный режим.
Представленная на рис. 8 схема называется схемой трех ваттметров.
Суммарная активная мощность цепи определяется как сумма показаний трех ваттметров
.
2. Четырехпроводная система, симметричный режим.
Если режим работы цепи симметричный, то для определения суммарной активной мощности достаточно ограничиться одним ваттметром (любым), включаемым по схеме на рис. 8. Тогда, например, при включении прибора в фазу А,
| . | (4) |
3. Трехпроводная система, симметричный режим.
При отсутствии доступа к нейтральной точке последняя создается искусственно с помощью включения трех дополнительных резисторов по схеме «звезда», как показано на рис. 9 – схема ваттметра с искусственной нейтральной точкой.
При этом необходимо выполнение условия , где — собственное сопротивление обмотки ваттметра. Тогда суммарная активная мощность трехфазной системы определяется согласно (4).
4. Трехпроводная система, симметричный режим; измерение реактивной мощности.
С помощью одного ваттметра при симметричном режиме работы цепи можно измерить ее реактивную мощность. В этом случае схема включения ваттметра будет иметь вид по рис. 10,а. Согласно векторной диаграмме на рис. 10,б измеряемая прибором мощность
Таким образом, суммарная реактивная мощность
5. Трехпроводная система, несимметричный режим.
Представленная на рис. 11 схема называется схемой двух ваттметров. В ней сумма показаний приборов равна суммарной активной мощности цепи.
Действительно, показания приборов в данной схеме:
.
Тогда
В заключение отметим, что если в схеме на рис. 11 имеет место симметричный режим работы, то на основании показаний приборов можно определить суммарную реактивную мощность цепи
| . | (5) |
Литература
- Основы
теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с. - Бессонов Л.А.
Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Контрольные вопросы и задачи
- В симметричной трехпроводной цепи произошел обрыв фазы. Что покажет вольтметр, включенный между найтральными точками источника и приемника?
- Во сколько раз мощность в цепи на рис. 6,а меньше мощности в цепи на рис. 4,а?
- В цепи на рис. 10,а симметричная нагрузка составлена из резистивных элементов. Что покажет ваттметр?
- В цепи на рис. 10,а симметричная нагрузка с фазным сопротивлением соединена в звезду. Линейное напряжение .
- В цепи на рис. 11 нагрузкой служат два одинаковых конденсатора с ХС=100 Ом, включенные между линейными проводами А и В, В и С соответственно. Линейное напряжение .
- На основе построения векторной диаграммы токов и напряжений для симметричного режима работы цепи на рис. 11 доказать соотношение (5).
Ответ: .
Ответ: в два раза.
Ответ: .
Определить показание ваттметра.
Ответ: .
Определить показания ваттметров.
Ответ: .
Как сделать лучевую векторную диаграмму связей в Excel
Сначала взглянем на то, что мы пытаемся построить и визуально оценим объем работы. Выглядит интересно? Тогда читайте дальше, чтобы узнать, как это создать.
Чтобы создать лучевую диаграмму в Excel для визуального анализа взаимоотношений в сети, нам нужно сначала понять ее различные составляющие.
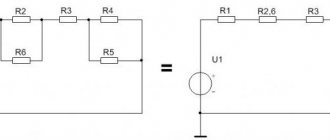
Как видите, диаграмма содержит следующие части:
- Набор точек, каждая из которых представляет одну заинтересованную сторону – участники сети.
- Набор сероватых толстых сплошных и тонких пунктирных линий, представляющих все отношения между людьми. Сплошные – сильные связи (например, друзья), пунктирные – слабые связи (знакомые).
- Набор зеленых толстых и синих пунктирных линий, представляющих отношения для выбранного конкретного участника сетевой группы.
- Срез для выбора анализа участника – как панель управления лучевой диаграммой.
- Табличка со сводной статистикой выбранного человека.