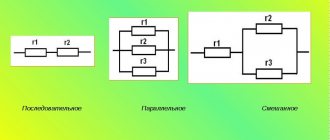
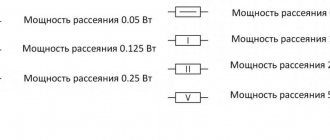
Все известные виды проводников обладают определенными свойствами, в том числе и электрическим сопротивлением. Это качество нашло свое применение в резисторах, представляющих собой элементы цепи с точно установленным сопротивлением. Они позволяют выполнять регулировку тока и напряжения с высокой точностью в схемах. Все подобные сопротивления имеют свои индивидуальные качества. Например, мощность при паралл ельном и последовательном соединении резисторов будет различной. Поэтому на практике очень часто используются различные методики расчетов, благодаря которым возможно получение точных результатов.
Пример задачи
Два проводника сопротивлением $R_1 = 2 \space Ом$ и $R_2 = 3 \space Ом$ соединены последовательно. Сила тока в цепи равна $1 \space А$. Определите сопротивление цепи, напряжение на каждом проводнике и полное напряжение всего участка цепи.
Так как проводники соединены последовательно, мы будем использовать формулы, полученные на данном уроке.
Дано: $R_1 = 2 \space Ом$ $R_2 = 3 \space Ом$ $I = 1 \space А$
$R — ?$ $U_1 — ?$ $U_2 — ?$ $U — ?$
Решение:
Общее сопротивление цепи будет равно сумме сопротивлений составляющих ее проводников: $R = R_1 + R_2$.
Рассчитаем его: $R = 2 \space Ом + 3 \space Ом = 5 \space Ом$.
Сила тока на всех участках цепи будет одинакова и равна $1 \space А$.
Запишем закон Ома для участка цепи с первым проводником и выразим из него напряжение на концах первого проводника: $I = \frac{U_1}{R_1}$, $U_1 = IR_1$.
Рассчитаем его: $U_1 = 1 \space А \cdot 2 \space Ом = 2 \space В$.
Так же рассчитаем напряжение на концах второго проводника: $I = \frac{U_2}{R_2}$, $U_2 = IR_2$, $U_2 = 1 \space А \cdot 3 \space Ом = 3 \space В$.
При последовательном соединении проводников полное напряжение в цепи мы можем рассчитать двумя способами.
Способ №1 Напряжение на всей цепи равно сумме напряжений на концах проводников в этой цепи: $U = U_1 + U_2$, $U = 2 \space В + 3 \space В = 5 \space В$.
Способ №2 Мы уже знаем общее сопротивление двух проводников. Получается, что эти два проводника мы можем представить как один целый. Используем закон Ома для участка цепи: $I = \frac{U}{R}$, $U = IR$, $U = 1 \space А \cdot 5 \space Ом = 5 \space В$.
Ответ: $R = 5 \space Ом$, $U_1 = 2 \space В$, $U_2 = 3 \space В$, $U = 5 \space В$.
Смешанное соединение
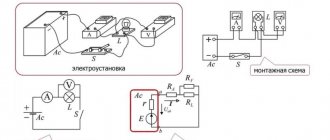
Схемы со смешанным соединением резисторов содержат последовательное и одновременно параллельное соединение. Эту схему несложно преобразовать, заменив параллельное соединение резисторов последовательным. Для этого заменяют сначала сопротивления R2 и R6 на их общее R2,6, используя формулу, приведённую ниже:
R2,6=R2∙R6/R2+R6.
Точно так же заменяются два параллельных резистора R4, R5 одним R4,5:
R4,5=R4∙R5/R4+R5.
В результате получается новая, более простая схема. Обе схемы приведены ниже.
Мощность резисторов на схеме со смешанным соединением определяется по формуле:
P=U∙I.
Для расчёта по этой формуле сначала находят напряжение на каждом сопротивлении и величину тока через него. Можно использовать другой метод, чтобы определить мощность резисторов. Для этого используется формула:
P=U∙I=(I∙R)∙I=I2∙R.
Если известно только напряжение на резисторах, то применяют другую формулу:
P=U∙I=U∙(U/R)=U2/R.
Все три формулы часто используются на практике.
Давайте рассмотрим немного расчетов по подключению ТЭНов.
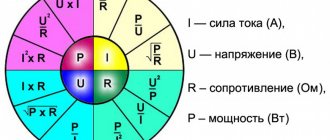
Общие формулы
| Мощность (Ватт) |
| Напряжение (Вольт) |
| Сила тока (Ампер) |
| Сопротивление (Ом) |
Рассмотрим последовательное или параллельное подключение нескольких одинаковых нагревательных элементов с различными схемами соединения. Для произведения расчетов нам понадобятся такие характеристики:
R = полное сопротивление P = общая мощность U и I соответственно напряжение и сила тока
Сопротивление в цепи при последовательном соединении проводников
Как найти общее сопротивление цепи, зная сопротивление отдельных проводников, при последовательном соединении?
Давайте порассуждаем. В цепи был один проводник с определенным сопротивлением. Мы последовательно подключаем второй. Представим эти два проводника в виде одного элемента цепи. Тогда получается, что, подсоединив второй проводник, мы увеличили длину первого.
Сопротивление же зависит от длины проводника. Поэтому суммарное сопротивление цепи будет точно больше сопротивления одного проводника.
Общее сопротивление цепи при последовательном соединении равно сумме сопротивлений отдельных проводников (или отдельных участков цепи): $R = R_1 + R_2 + … + R_n$.
На схемах электрических цепей последовательное соединение нескольких проводников изображается так, как показано на рисунке 4.
Рисунок 4. Последовательное соединение проводников на схеме электрической цепи
Резисторы
Соединяем последовательно
[Сопротивление последовательно соединенных резисторов, кОм
] = [
Сопротивление первого резистора, кОм
] + [
Сопротивление второго резистора, кОм
]
[Мощность, рассеиваемая первым резистором, Вт
] = [
Сопротивление первого резистора, кОм
] * [
Сила тока, мА
] ^ 2 / 1000
[Мощность, рассеиваемая вторым резистором, Вт
] = [
Сопротивление второго резистора, кОм
] * [
Сила тока, мА
] ^ 2 / 1000
Получается, что из двух резисторов по 500 Ом на 2 Вт можно сделать один на 1 кОм, 4 Вт.
Включаем параллельно
[Сопротивление параллельно соединенных резисторов, кОм
] = 1 / (1 / [
Сопротивление первого резистора, кОм
] + 1 / [
Сопротивление второго резистора, кОм
])
Эта формула интуитивно понятна, да и формально может быть выведена из следующего соображения. При заданном напряжении на резисторах через каждый из них независимо идет ток, равный напряжению, деленному на сопротивление. Итоговое сопротивление равно напряжению, деленному на суммарный ток. В формулах значение напряжения счастливым образом сокращается, и получается приведенная формула.
[Мощность, рассеиваемая первым резистором, Вт
] = [
Напряжение на резисторах, В
] ^ 2 / [
Сопротивление первого резистора, кОм
] / 1000
[Мощность, рассеиваемая вторым резистором, Вт
] = [
Напряжение на резисторах, В
] ^ 2 / [
Сопротивление первого резистора, кОм
] / 1000
Получается, что из двух резисторов по 500 Ом на 2 Вт можно сделать один на 250 Ом, 4 Вт.
К сожалению в статьях периодически встречаются ошибки, они исправляются, статьи дополняются, развиваются, готовятся новые. Подпишитесь, на новости, чтобы быть в курсе.
Практика проектирования электронных схем. Самоучитель электроники. Искусство разработки устройств. Элементная база радиоэлектроники. Типовые схемы.
Применение тиристоров (динисторов, тринисторов, симисторов). Схемы. Ис. Тиристоры в электронных схемах. Тонкости и особенности использования. Виды тирис.
Биполярный транзистор. Принцип работы. Применение. Типы, виды, категор. Все о биполярном транзисторе. Принцип работы. Применение в схемах. Свойства. Кла.
Плавная регулировка яркости свечения люминесцентных ламп дневного свет. Схема драйвера для плавной регулировки яркости свечения ламп дневного света. Дра.
Проверка электронных элементов, радиодеталей. Проверить исправность, р. Как проверить исправность детали. Методика испытаний. Какие детали можно использ.
RC — цепь. Резисторно — конденсаторная схема. Резистор, конденсатор. И. Расчет RC — цепи, изменения напряжения на конденсаторе в зависимости от времени.
Как правильно подключать нагреватели: параллельно или последовательно?
Итак, следует ли подключать нагреватели параллельно или последовательно? Этот вопрос возникает, когда к источнику питания необходимо подключить более одного нагревателя. Любое количество нагревателей может быть подключено параллельно, но обычно только два нагревателя подключаются последовательно. Надежное последовательное подключение более двух нагревателей является сложной задачей. Если нагреватели соединены последовательно, отказ одного нагревателя останавливает работу всех ТЭНов в цепочке. При параллельном подключении нагревателей отказ одного ТЭНа обычно не влияет на другие нагреватели.
Чаще всего при подключении используется два ТЭНа. В этом случае, если нагреватели соединены последовательно, напряжение каждого ТЭНа должно быть равно половине общего доступного напряжения. Например, два нагревателя на 240 вольт, подключенные последовательно к источнику питания на 480 вольт. Также мощность каждого нагревателя должна быть одинаковой. (Если мощность и напряжение каждого нагревателя не равны, нагреватели не будут делить общее напряжение поровну.) Если два нагревателя подключены параллельно, напряжение каждого нагревателя должно быть таким же, как напряжение питания.
Мощность при паралл ельном соединение
При паралл ельном подключении все начала резисторов соединяются с одним узлом схемы, а концы – с другим. В этом случае происходит разветвление тока, и он начинает протекать по каждому элементу. В соответствии с законом Ома, сила тока будет обратно пропорциональна всем подключенным сопротивлениям, а значение напряжения на всех резисторах будет одним и тем же.
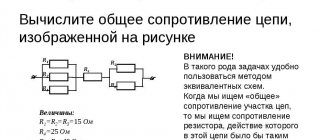
Прежде чем вычислять силу тока, необходимо выполнить расчет полной проводимости всех резисторов, применяя следующую формулу:
- 1/R = 1/R1+1/R2+1/R3+1/R4 = 1/200+1/100+1/51+1/39 = 0,005+0,01+0,0196+0,0256 = 0,06024 1/Ом.
- Поскольку сопротивление является величиной, обратно пропорциональной проводимости, его значение составит: R = 1/0,06024 = 16,6 Ом.
- Используя значение напряжения в 100 В, по закону Ома рассчитывается сила тока: I = U/R = 100 x 0,06024 = 6,024 A.
- Зная силу тока, мощность резисторов, соединенных паралл ельно, определяется следующим образом: P = I 2 x R = 6,024 2 x 16,6 = 602,3 Вт.
- Расчет силы тока для каждого резистора выполняется по формулам: I1 = U/R1 = 100/200 = 0,5A; I2 = U/R2 = 100/100 = 1A; I3 = U/R3 = 100/51 = 1,96A; I4 = U/R4 = 100/39 = 2,56A. На примере этих сопротивлений прослеживается закономерность, что с уменьшением сопротивления, сила тока увеличивается.
Существует еще одна формула, позволяющая рассчитать мощность при паралл ельном подключении резисторов: P1 = U 2 /R1 = 100 2 /200 = 50 Вт; P2 = U 2 /R2 = 100 2 /100 = 100 Вт; P3 = U 2 /R3 = 100 2 /51 = 195,9 Вт; P4 = U 2 /R4 = 100 2 /39 = 256,4 Вт. Сложив мощности отдельных резисторов, получится их общая мощность: Р = Р1+Р2+Р3+Р4 = 50+100+195,9+256,4 = 602,3 Вт.
Таким образом, мощность при последовательном и паралл ельном соединении резисторов определяется разными способами, с помощью которых можно получить максимально точные результаты.
При проектировании электрических схем возникает необходимость использования последовательного и параллельного соединений резисторов.
Соединения применяются также и при ремонтах электрооборудования, поскольку в некоторых ситуациях невозможно найти эквивалентный номинал резистора. Выполнить расчет просто, и справиться с этой операцией может каждый.
Сила тока в цепи при последовательном соединении проводников
При изучении силы тока мы измеряли ее на различных участках электрической цепи (рисунок 3). Полученные с помощью амперметра значения силы тока были одинаковы.
Рисунок 3. Измерение силы тока на различных участках электрической цепи при последовательном соединении ее элементов
При этом все элементы у нас были соединены последовательно. Сделаем вывод.
При последовательном соединении сила тока в любых частях цепи одна и та же: $I = I_1 = I_2 = … = I_n$.
Напряжение в цепи при последовательном соединении проводников
Используя закон Ома для участка цепи, мы можем найти напряжение и на концах этих участков: $U_1 = IR_1$, $U_2 = IR_2$, … $U_n = IR_n$.
Получается, что напряжение будет тем больше, чем больше сопротивление на участках цепи. Сила тока же везде будет одинакова.
Как найти напряжение участка цепи, состоящего из последовательно соединенных проводников, зная напряжение на каждом?
Полное напряжение в цепи при последовательном соединении, или напряжение на полюсах источника тока, равно сумме напряжений на отдельных участках цепи: $U = U_1 + U_2 + … + U_n$.