В этой статье мы расскажем вам, что представляет собой мощность электрического тока и как её можно рассчитать.
Определение.
Мощность электрического тока (обозначается буквой P) — это физическая величина, определяемая как количество работы, которая совершается источником электрического напряжения для переноса электрического заряда (q) по проводнику за единицу времени t.
Если сказать в целом, то мощность электрического тока показывает, сколько электрической энергии преобразуется за определенное время. Она, в том числе, описывает энергопотребление потребителя.
Формулы
На многих бытовых электроприёмниках есть этикетки с указанием мощности. Мощность (P) говорит о работе (A), выполняемой электроприбором в единицу времени (t). Поэтому, дабы отыскать среднюю мощность электрического тока, необходимо поделить его работу на время, то есть P = A / t.
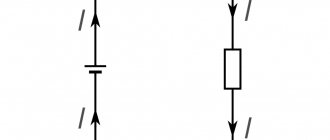
Давайте рассмотрим, что такое мощность электрического тока. Для этого рассмотрим электрическую цепь (см. рисунок 1), состоящую из источника тока, проводов и какого-либо электроприёмника, которым может быть резистор, аккумулятор, электродвигатель и т.д.
Рис. 1. Электрическая цепь, в которой напряжение и ток постоянны
Рекомендуемое электрическое напряжение также указывается на электрооборудовании. Как эти две величины связаны друг с другом? Из школьного курса физики мы знаем, что напряжение (U) между концами данного электроприёмника определяется следующим образом: U = A / q, где: A — работа, совершаемая источником электрического напряжения для переноса электрического заряда (q) по проводнику.
Величина электрического заряда рассчитывается по формуле: q = I * t
Имеем A = P * t; A = U*q, а q = I * t. После преобразования формул получаем: A = P*t = U*q = U*I*t
Отсюда следует (разделив обе стороны уравнения на t), что P = U*I. То есть мы можем сказать, что количество энергии, переданное от источника тока к резистору определяется по формуле: P = U * I
Из этой формулы можно найти, что U = P / I , I = P / U.
Согласно закону Ома для участка цепи I = U/R, где R — электрическое сопротивление участка цепи. Потому из формулы P = U*I следуют две другие формулы для мощности электрического тока, то есть P = U2/R, P = I2R.
Формулу P = I2R комфортно применять для электрических цепей с последовательным соединением проводников, потому что сила электрического тока при таком соединении в проводниках одинакова.
Для параллельно соединенных проводников работу и мощность удобнее выражать через одинаковое для их электрическое напряжение, исключая силу электрического тока, т.е. лучше применять формулу P = U2/R.
Если электроприборы соединены последовательно либо параллельно, их электрическая мощность суммируется. В данном случае для расчета полной мощности употребляется такая формула:
Pобщ = P1 + P2 + … + Pn, где P1 , P2 , … — мощность отдельно взятых электроприёмников.
1.11. Работа и мощность тока
При протекании тока по однородному участку цепи электрическое поле совершает работу. За время Δt по цепи протекает заряд Δq = I Δt. Электрическое поле на выделенном учестке совершает работу
| ΔA = (φ1 – φ2) Δq = Δφ12 I Δt = U I Δt, |
где U = Δφ12 – напряжение. Эту работу называют работой электрического тока.
Если обе части формулы
| RI = U, |
выражающей закон Ома для однородного участка цепи с сопротивлением R, умножить на IΔt, то получится соотношение
| R I2 Δt = U I Δt = ΔA. |
Это соотношение выражает закон сохранения энергии для однородного участка цепи.
Работа ΔA электрического тока I, протекающего по неподвижному проводнику с сопротивлением R, преобразуется в тепло ΔQ, выделяющееся на проводнике.
| ΔQ = ΔA = R I2 Δt. |
Закон преобразования работы тока в тепло был экспериментально установлен независимо друг от друга Дж. Джоулем и Э. Ленцем и носит название закона Джоуля–Ленца.
Мощность электрического тока равна отношению работы тока ΔA к интервалу времени Δt, за которое эта работа была совершена:
Работа электрического тока в СИ выражается в джоулях (Дж), мощность – в ваттах (Вт).
Рассмотрим теперь полную цепь постоянного тока, состоящую из источника с электродвижущей силой и внутренним сопротивлением r и внешнего однородного участка с сопротивлением R. Закон Ома для полной цепи записывается в виде
| (R + r) I = . |
Умножив обе части этой формулы на Δq = IΔt, мы получим соотношение, выражающее закон сохранения энергии для полной цепи постоянного тока:
| R I2Δt + r I2Δt = IΔt = ΔAст. |
Первый член в левой части ΔQ = R I2Δt – тепло, выделяющееся на внешнем участке цепи за время Δt, второй член ΔQист = r I2Δt – тепло, выделяющееся внутри источника за то же время.
Выражение IΔt равно работе сторонних сил ΔAст, действующих внутри источника.
При протекании электрического тока по замкнутой цепи работа сторонних сил ΔAст преобразуется в тепло, выделяющееся во внешней цепи (ΔQ) и внутри источника (ΔQист).
| ΔQ + ΔQист = ΔAст = IΔt |
.
Следует обратить внимание, что в это соотношение не входит работа электрического поля. При протекании тока по замкнутой цепи электрическое поле работы не совершает; поэтому тепло производится одними только сторонними силами, действующими внутри источника. Роль электрического поля сводится к перераспределению тепла между различными участками цепи.
Внешняя цепь может представлять собой не только проводник с сопротивлением R, но и какое-либо устройство, потребляющее мощность, например, электродвигатель постоянного тока. В этом случае под R нужно понимать эквивалентное сопротивление нагрузки. Энергия, выделяемая во внешней цепи, может частично или полностью преобразовываться не только в тепло, но и в другие виды энергии, например, в механическую работу, совершаемую электродвигателем. Поэтому вопрос об использовании энергии источника тока имеет большое практическое значение.
Полная мощность источника, то есть работа, совершаемая сторонними силами за единицу времени, равна
Во внешней цепи выделяется мощность Отношение равное
называется коэффициентом полезного действия источника.
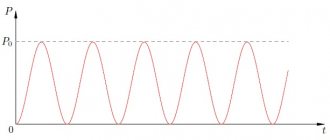
На рис. 1.11.1 графически представлены зависимости мощности источника Pист, полезной мощности P, выделяемой во внешней цепи, и коэффициента полезного действия η от тока в цепи I для источника с ЭДС, равной , и внутренним сопротивлением r. Ток в цепи может изменяться в пределах от I = 0 (при ) до (при R = 0).
| Рисунок 1.11.1. Зависимость мощности источника Pист, мощности во внешней цепи P и КПД источника η от силы тока |
Из приведенных графиков видно, что максимальная мощность во внешней цепи Pmax, равная
достигается при R = r. При этом ток в цепи а КПД источника равен 50 %. Максимальное значение КПД источника достигается при I → 0, т. е. при R → ∞. В случае короткого замыкания полезная мощность P = 0 и вся мощность выделяется внутри источника, что может привести к его перегреву и разрушению. КПД источника при этом обращается в нуль.
Единицы измерения и обозначение
Единицей измерения мощности в Международной системе единиц (СИ), является ватт. При этом русское обозначение: Вт, международное: W). 1 Вт = 1 Дж/c. Из формулы P = U*I следует, что: 1 ватт = 1 вольт * 1 ампер, или 1 Вт = 1 В*А.
Есть также единицы измерения мощности, кратные ваттам: гектаватт (гВт), киловатт (кВт), мегаватт (МВт). Другими словами 1 гВт = 100 Вт, 1 кВт = 1000 Вт, 1 МВт = 1 000 000 Вт.
Единицы мощности, применяемые в электротехнике, кратны ватту: микроватт (мкВт), милливатт (мВт), гектоватт (гВт), киловатт (кВт) и мегаватт (МВт). Другими словами, 1 мкВт = 1*10-6 Вт, 1 мВт = 1*10-3 Вт, 1 гВт = 1*102 Вт, 1 кВт = 1*103 Вт, 1 МВт = 1*106 Вт.
Каждый электроприбор имеет определенную мощность (указана на приборе). Вот типовые значения мощности для некоторых электроприборов.
| Прибор | Мощность, Вт |
| Телевизор в режиме ожидания | 0,5 |
| Лампа карманного фонарика | Около 1 |
| Лампы накаливания | 25-150 |
| Холодильник | 160 |
| Электронагреватель | 500-2000 |
| Пылесос | До 1300-1800 |
| Электрочайник | Около 2000 |
| Утюг | 1200-2200 |
| Стиральная машина | До 2300 |
Раньше для обозначения мощности использовалась единица измерения — лошадиная сила (л.с.), которая известна и сейчас. Переведите из лошадиных сил в ватты, используя выражение: 1 л.с. = 735.5 Вт.
Пример расчета мощности электрического тока
В конце концов, вы сможете проверить свои познания на 2-ух обычных примерах.
Представьте, что в первой задачке у вас есть резистор R = 50 Ом, через который течет электрический ток I = 0,3А. Какая электрическая мощность преобразуется в этом резисторе?
Вы можете отыскать решение, найдя соответствующую формулу и подставив в нее заданные значения. То есть у нас получается: P = I2R = 0,32 * 50 = 4,5 Вт
Во второй задаче дан резистор R, электрическое сопротивление которого 700 Ом. В техническом описании указано, что максимальная мощность этого резистора составляет 10 Вт. Насколько высоким может быть напряжение, подаваемое на этот резистор?
Для решения этой задачки подбираем подходящую формулу: P = U2/R, откуда мы находим Umax = Pmax * R = 700 * 10 = 83,67 В.
Это означает, что максимальное напряжение может составлять 83,67 В. Чтобы подстраховаться, следует выбирать электрическое напряжение значительно ниже этого предела.
Более подробно о том как можно находить мощность электрического тока я писал в статье:
Что такое КПД источника тока
Рассмотренный коэффициент полезного действия всей электрической цепи, позволяет лучше понять физическую суть КПД источника тока, формула которого также состоит из различных величин.
В процессе перемещения электрических зарядов по замкнутой электрической цепи, источником тока выполняется определенная работа, которая различается как полезная и полная. Во время совершения полезной работы, источника тока перемещает заряды во внешней цепи. При полной работе, заряды, под действием источника тока, перемещаются уже по всей цепи.
В виде формул они отображаются следующим образом:
- Полезная работа – Аполез = qU = IUt = I2Rt.
- Полная работа – Аполн = qε = Iεt = I2(R +r)t.
На основании этого, можно вывести формулы полезной и полной мощности источника тока:
- Полезная мощность – Рполез = Аполез /t = IU = I2R.
- Полная мощность – Рполн = Аполн/t = Iε = I2(R + r).
В результате, формула КПД источника тока приобретает следующий вид:
- η = Аполез/ Аполн = Рполез/ Рполн = U/ε = R/(R + r).
Максимальная полезная мощность достигается при определенном значении сопротивления внешней цепи, в зависимости от характеристик источника тока и нагрузки. Однако, следует обратить внимание на несовместимость максимальной полезной мощности и максимального коэффициента полезного действия.
Измерение мощности электрического тока
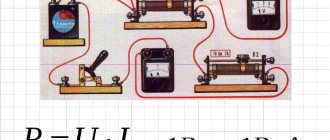
Вы сможете измерить силу электрического тока при помощи вольтметра и амперметра. Чтобы высчитать нужную мощность, помножьте электрическое напряжение на силу тока. Электрический ток и напряжение можно найти по показаниям приборов.
Рис. 2. Измерение мощности электрического тока
Помните, что вы всегда должны определять электрическое напряжение параллельно нагрузке и электрический ток последовательно.
Есть особые приборы – ваттметры, определяющие мощность электрического тока в цепи, которые, по сути, подменяют два устройства – амперметр и вольтметр.
Источник ЭДС
Для существования постоянного тока в цепи необходимо непрерывно разделять электрические заряды, которые под действием сил Кулона стремятся соединиться. Для этого необходимы сторонние силы. ЭДС характеризует действие этих сторонних сил. А сама эта работа осуществляется внутри источников ЭДС. Электрические заряды внутри источников ЭДС движутся против кулоновских сил под воздействием сторонних сил.
Сравнивая электрический ток с течением жидкости в трубах, можно сказать, что источник работает, как насос, который подает воду из нижнего резервуара в верхний, из которого она под действием силы тяжести стекает в нижний резервуар.
В быту «источником тока» часто неточно называют любой источник электрического напряжения (батарею, генератор, розетку), но в строго физическом смысле это не так, более того, обычно используемые в быту источники напряжения по своим характеристикам гораздо ближе к источнику ЭДС, чем к источнику тока из-за наличия внутреннего сопротивления.
В настоящее время выпускают множество различных источников ЭДС — от маленьких батареек для часов до генераторов.
Внутри источника тока происходит разделение зарядов из-за процессов, происходящих внутри источника, например, химических процессов.
Гальванический элемент
— химический источник тока, основанный на взаимодействии двух металлов и (или) их оксидов в электролите (батарейки, аккумуляторы).
Генераторы
— создают ток за счет расходования механической энергии.
Термоэлементы
— используют энергию теплового движения заряженных частиц.
Фотоэлементы
— создают ток за счет энергии света.
Единицы измерения электрического тока, применяемые на практике
В паспортах потребителей электроэнергии – лампочки, плиты, электродвигатели – обычно указывают силу электрического тока в них. Исходя из мощности, найти работу электрического тока за данный промежуток времени довольно просто, нужно лишь использовать формулу A = P*t.
Выразив мощность в ваттах, а время в секундах, мы получим работу в джоулях: 1 Вт = 1 Дж/с, где 1 Дж = 1 Вт*с.
Но эту единицу работы неудобно применять на практике, так как электроприёмники потребляют ее в течение долгих периодов времени, как, к примеру, в бытовых устройствах – в течение нескольких часов, в электропоездах – в течение нескольких часов либо даже суток, а расчет потребленной энергии по электросчетчику в большинстве случаев делается раз в месяц.
Потому при расчете работы тока либо затраченной и выработанной электроэнергии во всех этих случаях нужно переводить эти промежутки времени в секунды, что усложняет расчеты.
Перышкин А.В. Физика 8. – М.: Дрофа, 2010. [2]
Потому на практике, при расчете работы электрического тока, более удобно выражать время в часах, а работу электрического тока не в джоулях, а в других единицах: например, ватт-час (Вт*ч), гектоватт*час (гВт*ч), киловатт-час (кВт*ч).
Перышкин А.В. Физика 8. – М.: Дрофа, 2010. [2]
Будут верны следующие соотношения:
- 1 Вт*ч = 3600 Дж;
- 1 гВт*ч = 100 Вт*ч = 360 000 Дж;
- 1 кВт*ч = 1000 Вт*ч = 3 600 000 Дж.
Задача. Существует электрическая лампа, рассчитанная на ток в мощностью 100 ватт. Лампа работает в течение 6 часов каждый день. Нам нужно отыскать работу электрического тока за один месяц (30 дней) и стоимость потребленной электроэнергии, предполагая, что тариф составляет 500 копеек за один кВт/ч.
Запишем условие задачки и решим ее.
Входные данные: P = 100 Вт, t = 6 ч * 30 = 180 ч, тариф = 500 к / кВт*ч .
Решение задачи. Мы знаем, что A = P*t, потому получаем: A = 100 Вт*180 ч = 18 000 Вт*ч = 18 кВт*ч.
Мы рассчитываем стоимость так: Стоимость = 500 к / кВт*ч * 18 кВт*ч = 9000 копеек = 90 рублей.
Ответ: A = 18 кВт*ч, стоимость израсходованной электроэнергии = 90 рублей.
§ 22. Работа и мощность электрического тока
Способность тела производить работу называется энергией этого тела
. Например, поднятый на высоту какой-либо груз обладает некоторым запасом энергии и при падении производит работу. Работа измеряется в джоулях (
дж
). Энергия тела тем больше, чем большую работу может произвести это тело при своем движении. Энергия не исчезает, а переходит из одной формы в другую. Например, электрическая энергия может быть превращена в механическую, тепловую, химическую и т. д. Для переноса зарядов в замкнутой цепи источник электрической энергии затрачивает известную энергию, равную произведению э. д. с. источника на количество электричества, перенесенного через эту цепь, т. е.
A
0 =
E q
. Однако не вся энергия является полезной, т. е. не вся работа, произведенная источником энергии, сообщается приемнику энергии, так как часть ее расходуется на преодоление внутреннего сопротивления источника и проводов. Таким образом, источник электрической энергии производит полезную работу, равную
A
=
U q
,
где U
— напряжение на зажимах приемника,
в
. При неизменном токе количество электричества равно произведению силы тока в цепи на время его прохождения, т. е.
q
=
I t
,
тогда формулу работы можно представить в следующем виде:
A
=
U I t
, (28)
т. е. работа электрического тока равна произведению напряжения, силы тока в цепи и времени его прохождения
.
Если же выразить напряжение на зажимах участка цепи как произведение силы тока на сопротивление этого участка, т. е.
U
=
I r
,
то формулу работы можно записать и таким образом:
A
=
I
2
r t
. (29)
Однако ни одна из указанных формул не определяет размеров генератора электрической энергии, от которого получена эта работа, так как и большой и малый генераторы могут производить одинаковую работу, но в различные промежутки времени. Поэтому размеры генератора определяются не выполненной работой, а его мощностью. Зто относится к любому электротехническому аппарату и машине (электродвигатели, электрические лампы, нагревательные приборы и т. д.). Мощностью называется работа, производимая (или потребляемая) в одну секунду
. Мощность можно представить следующей формулой:
Если в формулах работы и мощности напряжение выражено в вольтах, сила тока — в амперах, сопротивление — в омах и время — в секундах, то работа выражается в ньютоно-метрах или в ватт-секундах (вт · сек
), т. е. в джоулях (
дж
), а мощность — в ваттах (
вт
). Для измерения малых мощностей применяют единицу, в тысячу раз меньшую 1
вт
, называемую милливаттом (
мвт
); 1
вт
= 1000
мвт
. Для измерения больших мощностей применяют единицу, в тысячу раз большую ватта, называемую киловаттом (
квт
); 1
квт
= 1000
вт
. Так как ватт-секунда (джоуль) является малой единицей, то работа обычно выражается в более крупных единицах: ватт-часах (
вт · ч
) и киловатт-часах (
квт · ч
). Соотношения между этими единицами и джоулем следующие: 1
вт · ч
= 3600
дж
; 1
квт · ч
= 3 600 000
дж
. Мощность во внешней цепи при напряжении
U
на зажимах генератора равна произведению напряжения на силу тока, т. е.
P = U I
.
При очень малом внешнем сопротивлении сила тока в цепи велика, а напряжение на зажимах генератора при этом мало. Если сопротивление внешней цепи равно нулю, то напряжение на зажимах генератора U
также равно нулю, следовательно и мощность
Р
, отдаваемая во внешнюю цепь, равна нулю. При очень большом внешнем сопротивлении (когда внешняя цепь разомкнута, сопротивление ее составляет бесконечно большую величину) сила тока в цепи равна нулю. Мощность, отдаваемая во внешнюю цепь, и в этом случае равна нулю. Таким образом с увеличением сопротивления внешней цепи мощность сначала возрастает от нуля до какой-то наибольшей (максимальной) величины, а затем убывает до нуля. Сопротивление внешней цепи
r
, при котором источник энергии отдает приемнику наибольшую мощность, равно внутреннему сопротивлению источника, т. е.
r
=
r
0. Однако надо иметь в виду, что при равенстве внутреннего сопротивления генератора сопротивлению внешней цепи полезная мощность генератора недостаточна и работа его в таких условиях неэкономична, так как половина всей мощности, развиваемой генератором, затрачивается на преодоление его внутреннего сопротивления.
Пример.
Источник энергии с э. д. с.
Е
= 120
в
и внутренним сопротивлением
r
0 = 10
ом
замыкается на нагрузку, сопротивление которой последовательно принимает следующие значения:
r
= 30; 20; 10; 5 и 2
ом
. Определить мощность, отдаваемую источником энергии во внешнюю цепь, при различных сопротивлениях нагрузки. Решение. Сила тока в замкнутой цепи и мощность во внешней цепи равны:
При сопротивлении нагрузки r
= 30
ом
при r
= 20
ом
при r
= 10
ом
при r
= 5
ом
при r
= 2
ом
Из рассмотренного примера видно, что наибольшая мощность во внешней цепи 360 вт
будет при сопротивлении нагрузки, равном внутреннему сопротивлению источника энергии, т. е.
r
=
r
0 = 10
ом
.
предыдущая страница
| оглавление | следующая страница |