In this article we will tell you what electrical power is and how it can be calculated.
Definition.
Electric current power (denoted by the letter P) is a physical quantity defined as the amount of work done by a source of electrical voltage to transfer electric charge (q) along a conductor per unit time t.
Generally speaking, the power of an electric current shows how much electrical energy is converted in a certain time. It also describes the consumer’s energy consumption.
Formulas
Many household electrical appliances have labels indicating their wattage. Power (P) refers to the work (A) performed by an electrical appliance per unit of time (t). Therefore, in order to find the average power of the electric current, it is necessary to divide its work by time, that is, P = A / t.
Let's look at what electric power is. To do this, consider an electrical circuit (see Figure 1), consisting of a current source, wires and some kind of electrical receiver, which can be a resistor, battery, electric motor, etc.
Rice. 1. An electrical circuit in which the voltage and current are constant
The recommended electrical voltage is also indicated on the electrical equipment. How are these two quantities related to each other? From a school physics course, we know that the voltage (U) between the ends of a given electrical receiver is determined as follows: U = A / q, where: A is the work done by the source of electrical voltage to transfer electric charge (q) along the conductor.
The amount of electric charge is calculated by the formula: q = I * t
We have A = P * t; A = U*q, and q = I * t. After transforming the formulas we get: A = P*t = U*q = U*I*t
It follows (by dividing both sides of the equation by t) that P = U*I. That is, we can say that the amount of energy transferred from the current source to the resistor is determined by the formula: P = U * I
From this formula we can find that U = P / I, I = P / U.
According to Ohm's law for a circuit section I = U/R, where R is the electrical resistance of the circuit section. Therefore, from the formula P = U*I, two other formulas for the power of electric current follow, that is, P = U2/R, P = I2R.
The formula P = I2R is convenient to use for electrical circuits with a series connection of conductors, because the strength of the electric current in such a connection in the conductors is the same.
For parallel-connected conductors, it is more convenient to express work and power through the same electrical voltage for them, excluding the strength of the electric current, i.e. it is better to use the formula P = U2/R.
If electrical appliances are connected in series or in parallel, their electrical power is summed up. In this case, to calculate the total power, the following formula is used:
Ptotal = P1 + P2 + … + Pn, where P1, P2, … is the power of individual electrical receivers.
1.11. Work and current power
When current flows through a homogeneous section of the circuit, the electric field does work. During the time Δt, a charge Δq = I Δt flows through the circuit. The electric field in a selected area does work
| ΔA = (φ1 – φ2) Δq = Δφ12 I Δt = UI Δt, |
where U = Δφ12 – voltage.
This work is called the work of electric current. If both sides of the formula
| RI = U, |
expressing Ohm's law for a homogeneous section of a circuit with resistance R, multiply by IΔt, you get the relation
| R I2 Δt = UI Δt = ΔA. |
This relationship expresses the law of conservation of energy for a homogeneous section of the chain.
The work ΔA of electric current I flowing through a stationary conductor with resistance R is converted into heat ΔQ released on the conductor.
| ΔQ = ΔA = R I2 Δt. |
The law of converting the work of current into heat was established experimentally independently of each other by J. Joule and E. Lenz and is called the Joule–Lenz law.
The power of the electric current is equal to the ratio of the current work ΔA to the time interval Δt during which this work was performed:
The work of an electric current in SI is expressed in joules (J), power - in watts (W).
Let us now consider a complete direct current circuit, consisting of a source with an electromotive force and internal resistance r and an external homogeneous section with resistance R. Ohm's law for the complete circuit is written as
| (R + r) I = . |
By multiplying both sides of this formula by Δq = IΔt, we obtain a relationship expressing the law of conservation of energy for a complete DC circuit:
| R I2Δt + r I2Δt = IΔt = ΔAst. |
The first term on the left side ΔQ = R I2Δt is the heat released in the external section of the circuit during the time Δt, the second term ΔQist = r I2Δt is the heat released inside the source during the same time.
The expression IΔt is equal to the work of external forces ΔAst acting inside the source.
When electric current flows through a closed circuit, the work of external forces ΔAst is converted into heat released in the external circuit (ΔQ) and inside the source (ΔQist).
| ΔQ + ΔQist = ΔAst = IΔt |
.
It should be noted that this ratio does not include the work of the electric field. When current flows through a closed circuit, the electric field does not do any work; therefore, heat is produced only by external forces acting inside the source. The role of the electric field is reduced to the redistribution of heat between different sections of the circuit.
The external circuit can be not only a conductor with resistance R, but also some device that consumes power, for example, a DC motor. In this case, R must be understood as the equivalent load resistance. The energy released in the external circuit can be partially or completely converted not only into heat, but also into other types of energy, for example, into mechanical work performed by an electric motor. Therefore, the question of using the energy of a current source is of great practical importance.
The total power of the source, that is, the work done by external forces per unit time, is equal to
The power released in the external circuit is equal to
is called the source efficiency factor.
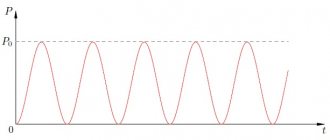
In Fig. 1.11.1 graphically shows the dependences of the source power Pist, the useful power P released in the external circuit, and the efficiency factor η on the current in the circuit I for a source with an emf equal to and internal resistance r. The current in the circuit can vary from I = 0 (at ) to (at R = 0).
| Figure 1.11.1. Dependence of source power Pist, power in the external circuit P and source efficiency η on current strength |
From the above graphs it is clear that the maximum power in the external circuit Pmax, equal to
is achieved at R = r. In this case, the current in the circuit and the efficiency of the source is 50%. The maximum value of the source efficiency is achieved at I → 0, i.e. at R → ∞. In the event of a short circuit, the useful power P = 0 and all the power is released inside the source, which can lead to its overheating and destruction. The efficiency of the source goes to zero.
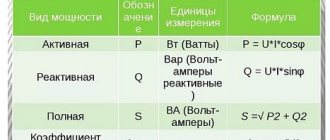
Units of measurement and designation
The unit of power in the International System of Units (SI) is the watt. In this case, the Russian designation: W , international: W ). 1 W = 1 J/s. From the formula P = U*I it follows that: 1 watt = 1 volt * 1 ampere, or 1 W = 1 VA.
There are also power units that are multiples of watts: hectawatt (gW), kilowatt (kW), megawatt (MW). In other words, 1 GW = 100 W, 1 kW = 1000 W, 1 MW = 1,000,000 W.
The units of power used in electrical engineering are multiples of the watt: microwatt (µW), milliwatt (mW), hectowatt (gW), kilowatt (kW) and megawatt (MW). In other words, 1 µW = 1*10-6 W, 1 mW = 1*10-3 W, 1 gW = 1*102 W, 1 kW = 1*103 W, 1 MW = 1*106 W.
Each electrical appliance has a certain power (indicated on the device). Here are typical wattage ratings for some electrical appliances.
| Device | Power, W |
| TV in standby mode | 0,5 |
| Flashlight lamp | About 1 |
| Incandescent lamps | 25-150 |
| Fridge | 160 |
| Electric heater | 500-2000 |
| Vacuum cleaner | Up to 1300-1800 |
| Electric kettle | Around 2000 |
| Iron | 1200-2200 |
| Washing machine | Up to 2300 |
Previously, the unit of measurement used to denote power was horsepower (hp), which is still known today. Convert from horsepower to watts using the expression: 1 hp. = 735.5 W.
An example of calculating the power of electric current
In the end, you will be able to test your knowledge with 2 common examples.
Imagine that in the first problem you have a resistor R = 50 Ohm through which an electric current I = 0.3A flows. What electrical power is converted in this resistor?
You can find the solution by finding the appropriate formula and plugging in the given values into it. That is, we get: P = I2R = 0.32 * 50 = 4.5 W
In the second problem, a resistor R is given, the electrical resistance of which is 700 Ohms. The technical description states that the maximum power of this resistor is 10 W. How high can the voltage applied to this resistor be?
To solve this problem, we select the appropriate formula: P = U2/R, from where we find Umax = Pmax * R = 700 * 10 = 83.67 V.
This means that the maximum voltage can be 83.67 V. To be on the safe side, you should choose an electrical voltage well below this limit.
I wrote in more detail about how to find the power of an electric current in the article:
What is the efficiency of a current source
The considered efficiency of the entire electrical circuit allows us to better understand the physical essence of the efficiency of the current source, the formula of which also consists of various quantities.
In the process of moving electric charges along a closed electrical circuit, a certain amount of work is performed by the current source, which is distinguished as useful and complete. While performing useful work, the current source moves charges in the external circuit. When fully operational, charges, under the influence of a current source, move throughout the entire circuit.
They are displayed as formulas as follows:
- Useful work – Apolez = qU = IUt = I2Rt.
- Total work – Total = qε = Iεt = I2(R +r)t.
Based on this, we can derive formulas for the useful and total power of the current source:
- Net power – Puse = Apoles /t = IU = I2R.
- Total power – Pfull = Afull/t = Iε = I2(R + r).
As a result, the formula for the efficiency of the current source takes the following form:
- η = Apoles/Atoll = Puse/Ptot = U/ε = R/(R + r).
Maximum useful power is achieved at a certain value of external circuit resistance, depending on the characteristics of the current source and load. However, attention should be paid to the incompatibility of maximum net power and maximum efficiency.
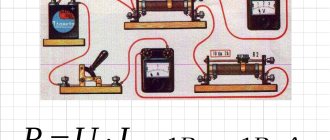
Electric current power measurement
You can measure the strength of electric current using a voltmeter and an ammeter. To calculate the required power, multiply the electrical voltage by the current. Electric current and voltage can be found from instrument readings.
Rice. 2. Electric current power measurement
Remember that you should always detect electrical voltage in parallel with the load and electrical current in series.
There are special devices - wattmeters - that determine the power of the electric current in a circuit, which, in fact, replace two devices - an ammeter and a voltmeter.
EMF source
For the existence of direct current in a circuit, it is necessary to continuously separate electric charges, which, under the influence of Coulomb forces, tend to connect. This requires outside forces. EMF characterizes the action of these external forces. And this work itself is carried out inside the EMF sources. Electric charges inside EMF sources move against Coulomb forces under the influence of external forces.
Comparing the electric current with the flow of liquid in the pipes, we can say that the source works like a pump that supplies water from the lower reservoir to the upper one, from which it flows under the influence of gravity into the lower reservoir.
In everyday life, a “current source” is often inaccurately called any source of electrical voltage (battery, generator, socket), but in a strictly physical sense this is not so; moreover, voltage sources usually used in everyday life are much closer in their characteristics to an EMF source than to current source due to the presence of internal resistance.
Currently, many different EMF sources are produced - from small watch batteries to generators.
Inside the current source, charge separation occurs due to processes occurring inside the source, for example, chemical processes.
Galvanic cell
- a chemical current source based on the interaction of two metals and (or) their oxides in an electrolyte (batteries, accumulators).
Generators
- create current by expending mechanical energy.
Thermoelements
- use the energy of thermal motion of charged particles.
Photocells
- create current using light energy.
Units of electrical current used in practice
The passports of electricity consumers - light bulbs, stoves, electric motors - usually indicate the strength of the electric current in them. Based on power, it is quite simple to find the work done by electric current over a given period of time; you just need to use the formula A = P*t.
Expressing power in watts and time in seconds, we get work in joules: 1 W = 1 J/s, where 1 J = 1 W*s.
But this unit of work is inconvenient to use in practice, since electrical receivers consume it over long periods of time, as, for example, in household appliances - for several hours, in electric trains - for several hours or even a day, and the calculation of consumed energy is based on In most cases, the electric meter is checked once a month.
Therefore, when calculating the work of a current or the energy consumed and generated, in all these cases it is necessary to convert these time periods into seconds, which complicates the calculations.
Peryshkin A.V. Physics 8. – M.: Bustard, 2010. [2]
Therefore, in practice, when calculating the work of electric current, it is more convenient to express time in hours, and the work of electric current not in joules, but in other units: for example, watt-hour (Wh), hectowatt-hour (gWh), kilowatt-hour (kW*h).
Peryshkin A.V. Physics 8. – M.: Bustard, 2010. [2]
The following relationships will be true:
- 1 Wh = 3600 J;
- 1 gWh = 100 Wh = 360,000 J;
- 1 kWh = 1000 Wh = 3,600,000 J.
Task. There is an electric lamp designed for a current of 100 watts. The lamp works for 6 hours every day. We need to find the work of electric current for one month (30 days) and the cost of consumed electricity, assuming that the tariff is 500 kopecks per kW/h.
Let's write down the condition of the problem and solve it.
Input data : P = 100 W, t = 6 h * 30 = 180 h, tariff = 500 kW/kWh.
The solution of the problem. We know that A = P*t, so we get: A = 100 W*180 h = 18,000 W*h = 18 kW*h.
We calculate the cost as follows: Cost = 500 kW*h * 18 kW*h = 9000 kopecks = 90 rubles.
Answer: A = 18 kWh, cost of consumed electricity = 90 rubles.
To main§ 22. Work and power of electric current
The ability of a body to produce work is called the energy of that body
.
For example, a load raised to a height has a certain amount of energy and produces work when falling. Work is measured in joules ( J
).
The energy of a body is greater, the more work this body can produce during its movement. Energy does not disappear, but passes from one form to another. For example, electrical energy can be converted into mechanical, thermal, chemical, etc. To transfer charges in a closed circuit, a source of electrical energy expends a known energy equal to the product of e. d.s. source on the amount of electricity transferred through this circuit, i.e. A
0 =
E q
. However, not all energy is useful, that is, not all the work done by the energy source is communicated to the energy receiver, since part of it is spent on overcoming the internal resistance of the source and wires. Thus, the source of electrical energy produces useful work equal to
A
=
U q
,
where U
— voltage at the receiver terminals,
in
. At a constant current, the amount of electricity is equal to the product of the current in the circuit and the time it passes, i.e.
q
=
I t
,
then the work formula can be presented as follows:
A
=
UI t
, (28)
i.e. the work of electric current is equal to the product of voltage, current strength in the circuit and the time it passes
.
If we express the voltage at the terminals of a section of the circuit as the product of the current strength and the resistance of this section, i.e.
U
=
Ir
,
then the work formula can be written as follows:
A
=
I
2
r t
. (29)
However, none of the above formulas determines the size of the electrical energy generator from which this work is obtained, since both large and small generators can produce the same work, but at different time intervals. Therefore, the size of the generator is determined not by the work performed, but by its power. This applies to any electrical apparatus and machine (electric motors, electric lamps, heating devices, etc.). Power is the work done (or consumed) in one second.
. Power can be represented by the following formula:
If in the work and power formulas voltage is expressed in volts, current in amperes, resistance in ohms and time in seconds, then work is expressed in newton-meters or watt-seconds ( W sec
), i.e. in joules (
J
), and power - in watts (
W
).
To measure low powers, a unit is used that is a thousand times smaller than 1 W
, called a milliwatt (
mW
);
1 W
= 1000
mW
.
To measure high powers, a unit a thousand times larger than the watt is used, called the kilowatt ( kW
);
1 kW
=
1000
W. Since the watt-second (joule) is a small unit, work is usually expressed in larger units: watt-hours ( w h
) and kilowatt-hours (
kw h
).
The relationships between these units and the joule are as follows: 1 W h
= 3600
J
;
1 kW h
=
3,600,000
J. The power in the external circuit at voltage U
at the generator terminals is equal to the product of voltage and current, i.e.
P=UI
.
With very low external resistance, the current in the circuit is high, and the voltage at the generator terminals is small. If the resistance of the external circuit is zero, then the voltage at the generator terminals U
is also equal to zero, therefore the power
P
given to the external circuit is equal to zero.
With a very large external resistance (when the external circuit is open, its resistance is infinitely large), the current in the circuit is zero. The power supplied to the external circuit is also zero in this case. Thus, with an increase in the resistance of the external circuit, the power first increases from zero to some largest (maximum) value, and then decreases to zero. The external circuit resistance r
, at which the energy source delivers the greatest power to the receiver, is equal to the internal resistance of the source, i.e.
r
=
r
0. However, it must be borne in mind that if the internal resistance of the generator is equal to the resistance of the external circuit, the useful power of the generator is insufficient and its work in such conditions it is uneconomical, since half of the total power developed by the generator is spent on overcoming its internal resistance.
Example.
Energy source with e.
d.s. E
= 120
V
and internal resistance
r
0 = 10
ohms
is closed to the load, the resistance of which sequentially takes the following values:
r
= 30;
20; 10; 5 and 2 ohms
. Determine the power supplied by the energy source to the external circuit at various load resistances. Solution. The current strength in the closed circuit and the power in the external circuit are equal:
With load resistance r
= 30
ohm
at r
= 20
ohm
at r
= 10
ohm
at r
= 5
ohms
at r
= 2
ohm
From the considered example it is clear that the maximum power in the external circuit is 360 W
will be with a load resistance equal to the internal resistance of the energy source, i.e.
r
=
r
0 = 10
ohm
.
Previous page
| table of contents | Next page |