What is deformation? Types of deformation
The phenomenon in which a change in the shape of a body occurs under the influence of some external force is called deformation. Its nature lies in the movement of molecules of a substance or entire layers of a crystal lattice, which leads to the appearance of so-called defects. The degree of deformation depends on many factors, among which we will consider mechanical stress.
There are several types of changes in body shape:
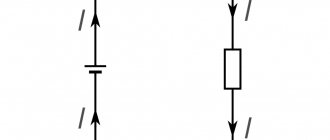
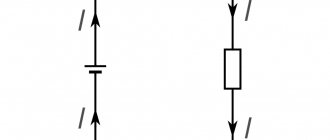
- Tensile deformation when an external force is applied along the entire body. Has practical value in the manufacture of ropes, cables and building materials;
- Compression strain. In this case, the vector of action of the external force coincides with the longitudinal axis of the body, but it is directed towards the center of this body. This type of deformation is used in the manufacture of metal and building materials to give them strength;
- Shear deformation occurs under the action of an external force, which is directed perpendicular to the longitudinal axis and causes the movement of different planes of the body relative to each other;
- Bending deformation is characterized by curvature of the main axis of the body, for example, when there are two points of support. The force that an object can withstand, as well as mechanical stress, play a big role in the creation of building materials;
- Torsional deformation occurs when a body rotates around its longitudinal axis. This type of deformation can be clearly demonstrated on a spring, which, after the cessation of the external force, will restore its shape.
Section method. Stresses: full, normal, tangential
To calculate strength of machine parts and assemblies, it is necessary to know the internal elastic forces that arise as a result of the action of external forces applied to the parts.
The section method is widely used in strength of materials to determine internal forces, so it is necessary to consider it in detail. Any body, including a part or machine assembly, can be represented as a system of material points.
In the strength of materials, changeable (deformable) systems of material points are considered.
The section method is
in that the body is mentally cut by a plane into two parts, any of which is discarded, and in return, internal forces that were acting before the cut are applied to the section of the remaining part. The remaining part is considered as an independent body, in equilibrium under the influence of external and internal forces applied to the section.
According to Newton's 3rd law (axiom of interaction), the internal forces acting in the cross section of the remaining and rejected parts of the body are equal in magnitude, but opposite in direction. Considering the equilibrium of any of the two parts of a dissected body, we obtain the same value of internal forces, but it is better to consider that part of the body for which the equilibrium equations are simpler.
According to the assumption of continuity of the material of the body, it can be argued that the internal forces arising in the body are forces uniformly or unevenly distributed over the cross section.
By applying equilibrium conditions to the remaining part of the body, one can find the law of distribution of internal forces over the section, as well as determine the static equivalents of these forces.
The main design object in the resistance of materials is a beam, and we are interested in the internal forces in its cross section, for which we consider the internal forces in the cross section of a beam.
Let's cut the beam (Fig. 1.) with cross section a - a
and consider the equilibrium of its left side.
Rice. 1. Equilibrium of the left side of the beam.
If the external forces acting on the beam lie in the same plane, then in the general case the static equivalent of the internal forces acting in the section a - a,
there will be
the main vector Fm
applied at the center of gravity of the section, and
the main moment MTL
- MI,
balancing the plane system of external forces applied to the remaining part of the beam.
Let us decompose the main vector into component N ,
directed along the axis of the beam, and component
Q
, perpendicular to this axis, that is, lying in the plane of the cross section.
We will call these components of the main vector, together with the main moment, internal force factors acting in the section of the beam. Component N
is called
longitudinal force
, component
Q
is called transverse force
, and a pair of forces with moment Mk is called bending moment.
To determine the indicated three internal force factors, statics gives three equilibrium equations for the remaining part of the beam, namely:
( z
always direct along the axis of the beam).
If the external forces acting on the beam do not lie in the same plane, then in the general case, six internal force factors arise in the cross section of the beam (Fig. 2), for the determination of which statics gives six equilibrium equations for the remaining part of the beam, namely:
Rice. 2. 6 internal force factors in the beam section.
The six internal force factors that arise in the cross section of a beam in the most general case have the following names: N -
longitudinal force,
Q
x,
Qy
- transverse forces,
Mk
- torque,
Msh, Miu
- bending moments.
With different deformations in the cross section of the beam, different internal force factors arise. Let's consider special cases.
1. Only longitudinal force N
In this case, it is a tensile deformation (if the force N is directed away from the section) or a compression deformation (if the force
N
is directed towards the section).
2. Q occurs in the section.
In this case, it is a shear deformation.
3. Only torque Mk occurs in the section.
In this case, it is a torsional deformation.
4. Only bending moment Mn occurs in the section.
In this case, it is pure bending deformation.
Mn
and a transverse force
occur simultaneously in a section ,
then the bending is called transverse.
5. Several internal force factors simultaneously arise in the section
(for example, bending and torque moments or bending moment and axial force). In these cases, a combination of basic deformations occurs.
Along with the concept of deformation, one of the main concepts of strength of materials is stress .
Stress characterizes the intensity of internal forces acting in a section.
Let's consider an arbitrarily loaded beam and apply the section method to it (Fig. 3). Let us select a small element of area dA in the section ,
considering the material continuous.
Due to the smallness of the element, we can assume that within its limits the internal forces applied at different points are identical in magnitude and direction and represent a system of parallel forces. We denote the resultant of this system as dF
. Dividing
dF
by the area of the elementary area
dA ,
we determine the intensity of the internal forces, that is, the voltage
p
at the points of the elementary area
dA
:
Rice. 3. Determination of stress p using the section method.
Thus, stress is an internal force per unit cross-sectional area.
Voltage is a vector quantity. Voltage unit:
This unit of stress is very small; a larger multiple of the unit is used, namely megapascal (MPa)
:
1 MPa = 106 Pa
=
1 N/mm2
.
Let us expand the voltage vector p
into two components:
Ϭ -
perpendicular to the section plane and
τ
- lying in the section plane (Fig. 1.5).
We will call these components normal
(
Ϭ
) and
tangential
(
τ
) stress, respectively.
Since the angle between the normal and tangential stresses is always 90°, the modulus of the total stress p
will be determined by the formula
The decomposition of the total stress into normal and tangential stress has a physical meaning. In the cross section of a beam, during tension, compression and pure bending, only normal stresses act, and during shear and torsion, only tangential stresses.
Let's consider a hypothesis called the principle of independence of the action of forces
and is formulated as follows:
when several loads act on a body, internal forces, stresses, displacements and deformations at any place can be determined as the sum of these quantities found from each load separately.
Using the principle of independence of the action of forces and starting with the study of the simplest basic deformations, when only normal or only tangential stresses act in the cross sections of a beam, we will later move on to the study of complex deformations, when both stresses act in the cross section, and consider cases of combination deformations, which are called complex resistance.
I would like to note that the principle of independent action of forces is applicable only for parts and assemblies whose deformations are small compared to their sizes and are proportional to the acting loads.
Assessment Questions
1. What is the section method?
2. What three internal force factors act in the cross section of the beam?
3. What parameter characterizes voltage?
4. In what units is voltage measured?
5. What components is the voltage vector divided into?
6. What stresses act during tension, compression and pure bending?
7. Formulate the principle of independence of forces.
To calculate strength of machine parts and assemblies, it is necessary to know the internal elastic forces that arise as a result of the action of external forces applied to the parts.
The section method is widely used in strength of materials to determine internal forces, so it is necessary to consider it in detail. Any body, including a part or machine assembly, can be represented as a system of material points.
In the strength of materials, changeable (deformable) systems of material points are considered.
The section method is
in that the body is mentally cut by a plane into two parts, any of which is discarded, and in return, internal forces that were acting before the cut are applied to the section of the remaining part. The remaining part is considered as an independent body, in equilibrium under the influence of external and internal forces applied to the section.
According to Newton's 3rd law (axiom of interaction), the internal forces acting in the cross section of the remaining and rejected parts of the body are equal in magnitude, but opposite in direction. Considering the equilibrium of any of the two parts of a dissected body, we obtain the same value of internal forces, but it is better to consider that part of the body for which the equilibrium equations are simpler.
According to the assumption of continuity of the material of the body, it can be argued that the internal forces arising in the body are forces uniformly or unevenly distributed over the cross section.
By applying equilibrium conditions to the remaining part of the body, one can find the law of distribution of internal forces over the section, as well as determine the static equivalents of these forces.
The main design object in the resistance of materials is a beam, and we are interested in the internal forces in its cross section, for which we consider the internal forces in the cross section of a beam.
Let's cut the beam (Fig. 1.) with cross section a - a
and consider the equilibrium of its left side.
Rice. 1. Equilibrium of the left side of the beam.
If the external forces acting on the beam lie in the same plane, then in the general case the static equivalent of the internal forces acting in the section a - a,
there will be
the main vector Fm
applied at the center of gravity of the section, and
the main moment MTL
- MI,
balancing the plane system of external forces applied to the remaining part of the beam.
Let us decompose the main vector into component N ,
directed along the axis of the beam, and component
Q
, perpendicular to this axis, that is, lying in the plane of the cross section.
We will call these components of the main vector, together with the main moment, internal force factors acting in the section of the beam. Component N
is called
longitudinal force
, component
Q
is called transverse force
, and a pair of forces with moment Mk is called bending moment.
To determine the indicated three internal force factors, statics gives three equilibrium equations for the remaining part of the beam, namely:
( z
always direct along the axis of the beam).
If the external forces acting on the beam do not lie in the same plane, then in the general case, six internal force factors arise in the cross section of the beam (Fig. 2), for the determination of which statics gives six equilibrium equations for the remaining part of the beam, namely:
Rice. 2. 6 internal force factors in the beam section.
The six internal force factors that arise in the cross section of a beam in the most general case have the following names: N -
longitudinal force,
Q
x,
Qy
- transverse forces,
Mk
- torque,
Msh, Miu
- bending moments.
With different deformations in the cross section of the beam, different internal force factors arise. Let's consider special cases.
1. Only longitudinal force N
In this case, it is a tensile deformation (if the force N is directed away from the section) or a compression deformation (if the force
N
is directed towards the section).
2. Q occurs in the section.
In this case, it is a shear deformation.
3. Only torque Mk occurs in the section.
In this case, it is a torsional deformation.
4. Only bending moment Mn occurs in the section.
In this case, it is pure bending deformation.
Mn
and a transverse force
occur simultaneously in a section ,
then the bending is called transverse.
5. Several internal force factors simultaneously arise in the section
(for example, bending and torque moments or bending moment and axial force). In these cases, a combination of basic deformations occurs.
Along with the concept of deformation, one of the main concepts of strength of materials is stress .
Stress characterizes the intensity of internal forces acting in a section.
Let's consider an arbitrarily loaded beam and apply the section method to it (Fig. 3). Let us select a small element of area dA in the section ,
considering the material continuous.
Due to the smallness of the element, we can assume that within its limits the internal forces applied at different points are identical in magnitude and direction and represent a system of parallel forces. We denote the resultant of this system as dF
. Dividing
dF
by the area of the elementary area
dA ,
we determine the intensity of the internal forces, that is, the voltage
p
at the points of the elementary area
dA
:
Rice. 3. Determination of stress p using the section method.
Thus, stress is an internal force per unit cross-sectional area.
Voltage is a vector quantity. Voltage unit:
This unit of stress is very small; a larger multiple of the unit is used, namely megapascal (MPa)
:
1 MPa = 106 Pa
=
1 N/mm2
.
Let us expand the voltage vector p
into two components:
Ϭ -
perpendicular to the section plane and
τ
- lying in the section plane (Fig. 1.5).
We will call these components normal
(
Ϭ
) and
tangential
(
τ
) stress, respectively.
Since the angle between the normal and tangential stresses is always 90°, the modulus of the total stress p
will be determined by the formula
The decomposition of the total stress into normal and tangential stress has a physical meaning. In the cross section of a beam, during tension, compression and pure bending, only normal stresses act, and during shear and torsion, only tangential stresses.
Let's consider a hypothesis called the principle of independence of the action of forces
and is formulated as follows:
when several loads act on a body, internal forces, stresses, displacements and deformations at any place can be determined as the sum of these quantities found from each load separately.
Using the principle of independence of the action of forces and starting with the study of the simplest basic deformations, when only normal or only tangential stresses act in the cross sections of a beam, we will later move on to the study of complex deformations, when both stresses act in the cross section, and consider cases of combination deformations, which are called complex resistance.
I would like to note that the principle of independent action of forces is applicable only for parts and assemblies whose deformations are small compared to their sizes and are proportional to the acting loads.
Assessment Questions
1. What is the section method?
2. What three internal force factors act in the cross section of the beam?
3. What parameter characterizes voltage?
4. In what units is voltage measured?
5. What components is the voltage vector divided into?
6. What stresses act during tension, compression and pure bending?
7. Formulate the principle of independence of forces.
Elastic and plastic deformation
Mechanical stress, which depends on the nature of the substance, affects the ability of the body to restore its original shape after a defect occurs in the crystal lattice. Based on this criterion, elastic and plastic deformation are distinguished.
With plastic deformation, the body, after exposure to an external force, is not able to restore its previous shape. For example, plasticine, when pressed with a finger, retains the resulting hole.
Elastic deformation is characteristic of those substances that are able to restore their original shape after being exposed to an external force. An example is the same spring, which, with any type of deformation described above, returns to its original state.
General information about aircraft engine technology
For his existence, a person needs material and cultural benefits, the sources of which are natural objects and human labor.Nature puts at human disposal a negligible number of objects that can be used directly, without human labor. Therefore, a person almost always has to expend labor in order, through qualitative transformation, to adapt objects of nature to satisfy his needs.
The qualitative change in natural objects carried out by man is called the technological process (TP). The word “technology” is formed from two Greek words: techne - art, science, craft and logos - teaching, i.e. - the doctrine of craft. Currently, this concept is given meaning to the body of knowledge about the means, methods, patterns and scientific principles of carrying out production processes (machining, stamping, assembly, etc.), which is the subject of the course. Mechanical engineering technology is a branch of science that studies the patterns that operate in the process of manufacturing machines, with the aim of using these patterns to ensure the required quality of machines and the lowest cost of producing them on time.
The efficiency of production in the country as a whole and labor productivity in all sectors of the economy depend on the total complex of technologies the state owns.
The manufacture of machines begins from the moment when the initial materials begin to be given the geometric parameters and physical and mechanical properties required for a given machine, i.e., from the manufacture of blanks for its parts and ends with testing the machine. In such a broad area as mechanical engineering technology, many processes of processing, processing and joining of materials and semi-finished products, different in physical essence and the necessary equipment, are used: various types of casting, pressure processing, explosion, cutting, electrochemical processing, chemical-thermal treatment, welding, soldering, assembly, surface coatings, etc. All these processes are studied in academic disciplines, which are basic in relation to mechanical engineering technology.
Aircraft engine manufacturing (ADS) is a sub-sector of the aviation industry that provides aircraft and helicopters with traction means, the weight, resource and economic characteristics of which determine the efficiency and profitability of operating the civil aviation aircraft fleet and the tactical and technical data of military aviation.
ADS refers to medium precision engineering, the features of which are: - Medium in size and overall dimensions of the product. for small-sized engines, the largest diameter is 500 mm; for medium engines diameter up to 1000mm; for large engines of transport aircraft – 3000mm; — High precision of parts and products. The requirements for high reliability of aircraft engines and assemblies are primarily related to trouble-free operation. (Of the total number of failures of airplanes and helicopters, 70% are due to the fault of aircraft engines, and 40% of them are due to the fault of units.) Therefore, the requirements for accuracy and quality of processing apply not only to mating surfaces, but also to free surfaces.
The mating surfaces of the engines are at the level of 6th quality, and in units 5.6-grade. The accuracy of the main parts of turbines and shafts is not lower than 8.9 quality.
The roughness of engine parts at the interface reaches Ra0.01 µm, and the average roughness is Ra2.5 µm. Some parts of the units have a roughness of Ra0.008 µm.
— Complexity of shapes and thin-walled parts. The specific gravity of a gas turbine engine is 30, 40 times less than that of a car engine. — Widespread use of difficult-to-process expensive materials. — Wide variety of processing methods used. — Relatively frequent change of production facilities.
Typical time frames for sustainable engine production: for military aviation 4...8 years; for civil aviation 10...15 years. Each aircraft plant produces simultaneously from 3-5 to 15-20 types of engines. All these requirements are ensured by the appropriate level of organization of the production process and the quality of development and debugging of the technological process (TP).
The production process is a set of actions carried out to transform materials and semi-finished products into a product. The production process covers:
- preparation of means of production;
- organization of workplace maintenance;
- receipt and storage of materials and semi-finished products;
- all stages of manufacturing, assembly and testing of products;
- transportation, technical control and sales of products.
TP is part of the production process that ensures the manufacture of parts.
Mechanical stress: formula and definition
The magnitude of mechanical stress is characterized by the internal forces of molecules, which are directed against the pressure and deformation of the body, per unit area.
There are two types of voltage:
- Normal stress is applied per unit area of the section parallel to the main axis of the body.
- The tangential mechanical stress is applied per unit sectional area of any other sectional plane.
To mathematically calculate mechanical stress, the formula is used: Q=F/S.