Electric current power: definition, formulas, units of measurement, designation

In this article we will tell you what electrical power is and how it can be calculated.

Definition.

Electric current power (denoted by the letter P) is a physical quantity defined as the amount of work done by a source of electrical voltage to transfer electric charge (q) along a conductor per unit time t.

Generally speaking, the power of an electric current shows how much electrical energy is converted in a certain time. It also describes the consumer’s energy consumption.

What is electric power

When describing electrical power in a broad sense, we are most often talking about the energy or force with which some object or action is endowed. For example, it can be defined for an explosion or a mechanism, such as an engine. This parameter is associated with force and depends on it, which is why these phenomena are often confused.

The difference is that force affects physical actions, that is, work is performed. If it is done in the specified time, then through these two parameters the power value can be calculated.

In the case of electricity, there are two types:

1. Active - turns into energy of heat, light, mechanical action, etc. It is measured in watts and calculated by the formula 1 W = 1 V x 1A. But in practice, this indicator is most often expressed in kilowatts and megawatts.
2. Reactive – load arising due to oscillations within the electromagnetic field. The unit of measurement is volt-amperes (VA), they are calculated as Q=U x I x sin angle. The latter means a phase change between current and voltage reduction.

In practice, the differences between both types are best seen using the example of heating elements and electric motors. Heating elements are assembled from a material with high resistance, so they convert all the electricity received into heat. The electric motor has parts that have inductance, that is, part of the current returns to the network and can negatively affect it, creating overloads.

Power unit

A unit of power is taken to be the power at which 1 J of work is done in 1 s.

This unit is called the watt (W) in honor of the scientist Watt (Figure 1).

Figure 1. James Watt (1736-1819) - Scottish engineer and inventor.

From the power formula $N = \frac{A}{t}$:

$$1 \space watt = \frac{1 \space joule}{1 \space second} = 1 \frac{J}{s}$$

Other power units often used are kilowatt (kW), megawatt (MW) and milliwatt (mW):

$1 \space MW = 1,000,000 \space W$

$1 \space W = 0.000001 MW$

$1 \space kW = 1000 \space W$

$1 \space W = 0.001 kW$

$1 \space mW = 0.001 \space W$

$1 \space W = 1000 \space mW$

Power is also sometimes measured in horsepower (hp):

$1 \space l. With. = 735.5 \space W$

$1 \space W = 0.00013596 \space hp$

This unit of measurement is not as popular as the watt, but is still used, for example, in the automotive industry.

How is power indicated?

P - electric current power is indicated (W).

In conclusion, it should be noted that total power has practical significance, as a value that describes the loads actually imposed by the consumer on the elements of the supply network (wires, cables, distribution boards, transformers, power lines), since these loads depend on the current consumed, and not from the energy actually used by the consumer. That is why this value of transformers and distribution boards is measured in volt-amperes, and not in watts.

Current power through the capacitor

Let an alternating voltage be applied to the capacitor. As we know, the current through a capacitor is ahead of the voltage in phase by:

For instantaneous power we get:

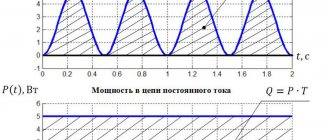
Graph of instantaneous power versus time.

AC power through a capacitor.

What is the average power value? It corresponds to the “middle” of the sinusoid and in this case is equal to zero! We see this now as a mathematical fact. But it would be interesting to understand from a physical point of view why the current power through the capacitor turns out to be zero.

To do this, let's draw graphs of the voltage and current in the capacitor over one oscillation period.

The voltage across the capacitor and the current through it.

Let's consider all four quarters of the period sequentially.

1. First quarter, . The tension is positive and increasing. The current is positive (flows in the positive direction), the capacitor is charged. As the charge on the capacitor increases, the current decreases.

Instantaneous power is positive: the capacitor stores energy coming from the external circuit. This energy arises due to the work of an external electric field that pushes charges onto the capacitor.

2. Second quarter, . The tension remains positive, but is subsiding. The current changes direction and becomes negative: the capacitor is discharged against the direction of the external electric field. At the end of the second quarter, the capacitor is completely discharged.

Instantaneous power is negative: the capacitor releases energy. This energy returns to the circuit: it is used to do work against the electric field of the external circuit (the capacitor, as it were, “pushes” the charges in the direction opposite to the one in which the external field “wants” to move them).

3. Third quarter, . The external electric field changes direction: the voltage is negative and increases in magnitude. The current is negative: the capacitor is charging in the negative direction.

The situation is completely similar to the first quarter, only the signs of voltage and current are opposite. The power is positive: the capacitor again stores energy.

4. Fourth quarter, . The voltage is negative and decreases in magnitude. The capacitor is discharged against the external field: the current strength is positive.

Power is negative: the capacitor returns energy to the circuit. The situation is similar to the second quarter - again with the replacement by replacing the signs of current and voltage with opposite ones.

We see that the energy taken by the capacitor from the external circuit during the first quarter of the oscillation period is completely returned to the circuit during the second quarter. This process is then repeated again and again. This is why the average power consumed by a capacitor turns out to be zero.

Concept of total power. Capacity Triangle

Apparent power is a geometrically calculated value equal to the root of the sum of the squares of active and reactive powers, respectively. Denoted by the Latin letter S.

You can also calculate the total power by multiplying the voltage and current respectively.

S = U⋅I

IMPORTANT! Apparent power is measured in volt-amperes (VA).

The power triangle is a convenient representation of all the previously described calculations and relationships between active, reactive and apparent power.

The legs reflect the reactive and active components, the hypotenuse – the full power. According to the laws of geometry, the cosine of the angle φ is equal to the ratio of the active and total components, that is, it is the power factor.

Electrical power and inactive power

Equipment certificates contain active load - power factor, which is an important characteristic. It shows how efficiently a household appliance consumes electricity.

Fig.8

This is a number from −1 to 1, it is never equal to one. This coefficient depends on the type of load: C, L or R. The first 2 negatively affect PF = cos φ of the system. If its parameter is large, the current consumed by the devices increases. Many power loads are inductive, causing the current to lag behind the voltage.

Inactive energy arises in electrical AC circuits of alternating current networks. It is calculated simply: the square root of the sum (Pa2 + Pr2). If the reactive load is zero, then the passive load is equal to the modulus |Pa|.

The presence of nonlinear current distortions in electrical networks is caused by non-compliance with the direction that occurs between U/I, since the energy has a pulsed nature. In nonlinear modes, the apparent current power (EP) increases. Such a load is inactive and consumes Pr and current distortion energy. The unit of measurement is the same as regular power W.

How to find out voltage by knowing current strength

To calculate the voltage, use the formulas:

U=P/I – direct current;

U=P/(I*cos(phi)) - single-phase network;

U=P/(1.73*I*cos(phi)) - three-phase network.

From the expression it can be seen that voltage is directly proportional to voltage and inversely proportional to current.

Electrical power: AC circuit

For such lines, it is unacceptable to use formulas that determine instantaneous parameters, since the final indicator changes from a minimum value to a maximum value with the network frequency. A typical single-phase 220 V network is characterized by a 50 Hz sinusoidal signal. It is allowed to use the simple formula P = U x I when connecting devices with resistive parameters:

• Heating elements of washing machines;
• spirals of infrared heaters;
• incandescent light bulbs.

Using this formula, the load is set.

How to calculate power knowing current and voltage

The power characteristics of electrical installations are calculated using the formula:

We recommend reading: Transistors and diodes: how semiconductors work

P=U*I - direct current;

P=U*I*cos(phi) – alternating current of a single-phase network.

P=1.73*U*I*cos(phi) - three-phase network.

The article provides simplified formulas for calculating the active power of the electrical network, which give approximate results.

To obtain accurate results, it is also necessary to take into account reactance and ordinary resistance, as well as losses.

Electrical current through voltage and current

Since the potential difference calculated by the formula (F1-F2) determines the voltage (U), it is easy to conclude that the relationship established by Ohm’s law cannot be used. Electrical power (P) is also qualified by the current strength (I) on a specific section of the line. Final expression: P = U x I.

What is the load determined in terms of current and resistance?

Through a simple conversion, the electrical energy consumption is determined using the following formula: P = I2 x R. This shows the dependence of the power on the nominal value of the resistor connected to the line of the network element. For a complete circuit, the source resistance (internal) and the conductance of the connection point are indicated.

How to calculate correctly

Active power, how to make the correct calculation?

The power of the electric current affects how quickly the device can complete the job. For example, an expensive heater with twice the power will heat a room faster than two cheap ones with half the power. It turns out that it is more profitable to buy a unit with more power in order to heat a cold room faster. But, at the same time, such a unit will consume significantly more energy than its cheaper counterpart.

The power consumption of all appliances in the house is also taken into account when selecting wiring for installation in the house. If you do not take this into account and subsequently connect too many devices to the network, this will cause network overload. The wiring will not be able to withstand the power of the electric current of all devices, which will lead to melting of the insulation, short circuit and self-ignition of the wiring. As a result, a fire may start, which can lead to irreparable consequences.

Single-phase sinusoidal current in electrical circuits is calculated by the formula P = U x I x cos φ, where υ and Ι. Their designation is encrypted as follows: the root mean square value of voltage and current, and φ is the phase angle between them.

For non-sinusoidal current circuits, the electrical capacitance is equal to the square root of the sum of the squares of the active and reactive performance. Active performance is characterized by the speed of the irreversible process of converting electrical energy into other types of energy. This capacitance can be calculated through the current, voltage and active component of the circuit resistance r or its conductivity g using the formula P = I(2) xr = U(2) x g.

Reactive Power

It should be noted that:

• The resistor consumes active power and releases it in the form of heat and light.
• inductance consumes reactive power and releases it in the form of a magnetic field.
• The capacitor consumes reactive power and releases it in the form of an electric field.

In any electrical circuit of both sinusoidal and non-sinusoidal current, the active capacity of the entire circuit is equal to the sum of the active powers of the individual parts of the circuit; for three-phase circuits, the electrical capacity is defined as the sum of the throughput of the individual phases. With the total performance S, the active one is related by the relation P = S x cos φ.

In the theory of long lines (the analysis of electromagnetic processes in a transmission line, the length of which is comparable to the length of the electromagnetic wave), the complete analogue of active power is transmitted power, which is defined as the difference between the incident power and the reflected performance.

How to find reactive apparent power through active power? This performance, which characterizes the loads created in electrical devices by fluctuations in the energy of the electromagnetic field in a sinusoidal alternating current circuit, is equal to the product of the rms values ​​of voltage U and current I, multiplied by the sine of the phase angle φ between them: Q = U x I x sin φ (if the current lags behind the voltage, the phase shift is considered positive, if it is ahead, it is negative).

Reactive quantity designation

An example of calculating the power of electric current

In the end, you will be able to test your knowledge with 2 common examples.

Imagine that in the first problem you have a resistor R = 50 Ohm through which an electric current I = 0.3A flows. What electrical power is converted in this resistor?

You can find the solution by finding the appropriate formula and plugging in the given values ​​into it. That is, we get: P = I2R = 0.32 * 50 = 4.5 W

In the second problem, a resistor R is given, the electrical resistance of which is 700 Ohms. The technical description states that the maximum power of this resistor is 10 W. How high can the voltage applied to this resistor be?

To solve this problem, we select the appropriate formula: P = U2/R, from where we find Umax = Pmax * R = 700 * 10 = 83.67 V.

This means that the maximum voltage can be 83.67 V. To be on the safe side, you should choose an electrical voltage well below this limit.

Current power through resistor

Let alternating current flow through a resistor with a resistance of . The voltage across the resistor, as we know, oscillates in phase with the current:

Therefore, for instantaneous power we obtain:

(2)

We see that the power is non-negative all the time - the resistor takes energy from the circuit, but does not return it back to the circuit.

AC power through a resistor.

The maximum value of our power is related to the amplitudes of current and voltage by the usual formulas:

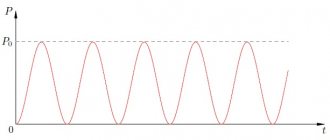
In practice, however, it is not the maximum, but the average current power that is of interest. This is understandable. Take, for example, an ordinary light bulb that is lit in your home. A current with a frequency of Hz flows through it, i.e., fluctuations in current and voltage occur per second. It is clear that over a sufficiently long time, a certain average power is released from the light bulb, the value of which is somewhere between and . Where exactly?

Look again carefully at Fig. 1. Don’t you have an intuitive feeling that the average power corresponds to the “middle” of our sinusoid and therefore takes on the value ?

This feeling is absolutely true! The way it is. Of course, we can give a mathematically strict definition of the average value of a function (in the form of some integral) and confirm our guess with direct calculation, but we don’t need this. An intuitive understanding of a simple and important fact is enough:

the average value of the square of the sine (or cosine) over the period is equal to .

The mean value of the squared sine is

So, for the average value of the current power across the resistor we have:

(3)

In connection with these formulas, the so-called effective (or effective) values ​​of voltage and current are introduced (in fact, these are nothing more than the root mean square values ​​of voltage and current. We have already encountered this: the root mean square speed of the molecules of an ideal gas (leaf "Equation of state of an ideal gas"):

(4)

Formulas (3), written in terms of effective values, are completely similar to the corresponding formulas for direct current:

Therefore, if you take a light bulb, connect it first to a constant voltage source, and then to an alternating voltage source with the same effective value, then in both cases the light bulb will burn equally brightly.

The effective values ​​(4) are extremely important for practice. It turns out that AC voltmeters and ammeters show exactly the effective values ​​(that’s how they are designed). Know also that the notorious volts from the outlet are the effective value of the household power supply voltage.

Power in mechanics[ | ]

If a force acts on a moving body, then this force does work. Power in this case is equal to the scalar product of the force vector and the velocity vector with which the body moves:

where F {\displaystyle \mathbf {F} } is the force vector;
v {\displaystyle \mathbf {v} } — velocity vector; α {\displaystyle \alpha } is the angle between the vector of velocity and force; F {\displaystyle F}—modulus of the force vector; v {\displaystyle v} is the magnitude of the velocity vector. A special case of power during rotational motion:

where M {\displaystyle \mathbf {M} } is the moment of force (N*m); ω {\displaystyle \mathbf {\omega } } — angular velocity (rad/s); n {\displaystyle n} — rotation speed (rpm, rpm).

Current power through the coil

Let alternating voltage be applied to the coil. The current through the coil lags in phase from the voltage by:

For instantaneous power we get:

Again the average power is zero. The reasons for this are, in general, the same as in the case of a capacitor. Let's look at the graphs of voltage and current through the coil over a period (Fig. 5).

The voltage across the coil and the current through it.

We see that during the second and fourth quarters of the period, energy enters the coil from the external circuit. In fact, voltage and current have the same signs, the current increases in magnitude; To create a current, the external electric field does work against the vortex electric field, and this work goes to increase the energy of the magnetic field of the coil.

In the first and third quarters of the period, the voltage and current have different signs: the coil returns energy to the circuit. The vortex electric field, which maintains a decreasing current, moves charges against the external electric field and thereby does positive work. How is this work accomplished? Due to the energy previously accumulated in the coil.

Thus, the energy stored in the coil during one quarter of the period is completely returned to the circuit during the next quarter. Therefore, the average power consumed by the coil is zero.