OGE 2022 in physics ›
1. Electric current, passing through a circuit, produces different effects: thermal, mechanical, chemical, magnetic. In this case, the electric field does work, and electrical energy is converted into other types of energy: internal, mechanical, magnetic field energy, etc.
As has been shown, the voltage \( (U) \) in a section of the circuit is equal to the ratio of the work \( (F) \) performed when moving an electric charge \( (q) \) in this section to the charge : \( U=A/q \). Hence \( A=qU \). Since the charge is equal to the product of current \( (I) \) and time \( (t) \) \( q=It \), then \( A=IUt \), i.e. . The work done by an electric current on a section of a circuit is equal to the product of the voltage on that section, the current strength and the time during which the work is performed.
The unit of work is the joule (1 J) . This unit can be expressed in terms of electrical units:
\( [A] \)= 1 J = 1 V · 1 A · 1 s
To measure work, three measuring instruments are used: ammeter, voltmeter and clock, however, in real life, electric energy meters are used to measure the work of electric current.
If you need to find the work done by a current, but the current strength or voltage is unknown, then you can use Ohm’s law, express the unknown quantities and calculate the work using the formulas: \( A=\frac{U^2}{R}t \) or \( A=I^2Rt \).
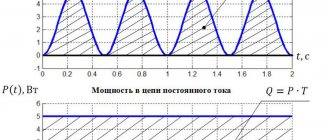
2. The power of the electric current is equal to the ratio of the work to the time during which it was completed: \( P=A/t \) or \( P=IUt/t \); \( P=IU \) , i.e. The power of the electric current is equal to the product of voltage and current in the circuit .
The unit of power is the watt (1 W): \( [P]=[I]\cdot[U] \); \( [P] \) = 1 A · 1 V = 1 W.
Using Ohm's law, you can obtain other formulas for calculating current power: \( P=\frac{U^2}{R};P=I^2R \).
The power of the electric current in a conductor can be determined using an ammeter and a voltmeter by measuring the current and voltage, respectively. To measure power, you can use a special device called a wattmeter, which combines an ammeter and a voltmeter.
3. When electric current passes through a conductor, it heats up. This happens because free electrons in metals and ions in electrolyte solutions moving under the influence of an electric field collide with molecules or atoms of conductors and transfer their energy to them. Thus, when work is done by the current, the internal energy of the conductor increases, a certain amount of heat is released in it, equal to the work done by the current, and the conductor heats up: \( Q=A \) or \( Q=IUt \). Considering that \( U=IR \), \( Q=I^2Rt \).
The amount of heat released when current passes through a conductor is equal to the product of the square of the current strength, the resistance of the conductor and time.
This law is called the Joule-Lenz law.
EXAMPLES OF TASKS
Part 1
1. The current strength in the conductor was increased by 2 times. How will the amount of heat released in it per unit time change if the resistance of the conductor remains constant?
1) will increase by 4 times 2) will decrease by 2 times 3) will increase by 2 times 4) will decrease by 4 times
2. The length of the electric stove spiral was reduced by 2 times. How will the amount of heat released in the spiral per unit time change at a constant network voltage?
1) will increase by 4 times 2) will decrease by 2 times 3) will increase by 2 times 4) will decrease by 4 times
3. The resistance of the resistor \( R_1 \) is four times less than the resistance of the resistor \( R_2 \). Current work in resistor 2
1) 4 times more than in resistor 1 2) 16 times more than in resistor 1 3) 4 times less than in resistor 1 4) 16 times less than in resistor 1
4. The resistance of the resistor \( R_1 \) is 3 times greater than the resistance of the resistor \( R_2 \). The amount of heat that will be released in resistor 1
1) 3 times more than in resistor 2 2) 9 times more than in resistor 2 3) 3 times less than in resistor 2 4) 9 times less than in resistor 2
5. The circuit is assembled from a current source, a light bulb and a thin iron wire connected in series. The light bulb will glow brighter if
1) replace the wire with a thinner iron one 2) reduce the length of the wire 3) swap the wire and the light bulb 4) replace the iron wire with nichrome
6. The figure shows a bar graph. It shows the voltage values at the ends of two conductors (1) and (2) of the same resistance. Compare the values of current work \( A_1 \) and \( A_2 \) in these conductors for the same time.
1) \( A_1=A_2 \) 2) \( A_1=3A_2 \) 3) \( 9A_1=A_2 \) 4) \( 3A_1=A_2 \)
7. The figure shows a bar graph. It shows the current values in two conductors (1) and (2) of the same resistance. Compare the values of current work \( A_1 \) and \( A_2 \) in these conductors for the same time.
1) \( A_1=A_2 \) 2) \( A_1=3A_2 \) 3) \( 9A_1=A_2 \) 4) \( 3A_1=A_2 \)
8. If you use lamps with a power of 60 and 100 W in a chandelier to illuminate the room, then
A. A large current will be in a 100 W lamp. B. A 60 W lamp has greater resistance.
The following statement(s) are true:
1) only A 2) only B 3) both A and B 4) neither A nor B
9. An electric stove connected to a direct current source consumes 108 kJ of energy in 120 s. What is the current strength in the tile spiral if its resistance is 25 Ohms?
1) 36 A 2) 6 A 3) 2.16 A 4) 1.5 A
10. An electric stove with a current of 5 A consumes 1000 kJ of energy. What is the time it takes for the current to pass through the spiral of the tile if its resistance is 20 Ohms?
1) 10000 s 2) 2000 s 3) 10 s 4) 2 s
11. The nickeline spiral of the electric stove was replaced with a nichrome one of the same length and cross-sectional area. Establish a correspondence between physical quantities and their possible changes when the tile is connected to the electrical network. Write down the selected numbers in the table under the corresponding letters. The numbers in the answer may be repeated.
PHYSICAL QUANTITY A) electrical resistance of the spiral B) electric current strength in the spiral B) electric current power consumed by the tile
NATURE OF CHANGE 1) increased 2) decreased 3) did not change
12. Establish a correspondence between physical quantities and the formulas by which these quantities are determined. Write down the selected numbers in the table under the corresponding letters.
PHYSICAL QUANTITIES A) current work B) current strength C) current power
FORMULAS 1) \( \frac{q}{t} \) 2) \( qU \) 3) \( \frac{RS}{L} \) 4) \( UI \) 5) \( \frac{U}{I} \)
Part 2
13. The heater is connected in series with a rheostat with a resistance of 7.5 Ohms in a network with a voltage of 220 V. What is the resistance of the heater if the power of the electric current in the rheostat is 480 W?
§ 13. Work and power of electric current
Electric Energy. In nature and technology, processes of energy conversion from one type to another continuously occur (Fig. 30). In electrical energy sources, various types of energy are converted into electrical energy. For example, in electric generators 1, driven by some mechanism, mechanical energy is converted into electrical energy, in thermogenerators 2 - thermal energy, in batteries 9 when they are discharged and galvanic cells 10 - chemical energy, in photocells 11 - radiant energy.
Receivers of electrical energy, on the contrary, convert electrical energy into other types of energy - thermal, mechanical, chemical, radiant, etc. For example, in electric motors 3 electrical energy is converted into mechanical energy, in electric heating devices 5 into thermal energy, in electrolytic baths 8 and batteries 7 when they are charged - into a chemical one, in electric lamps 6 - into radiant and thermal, in the antennas of 4 radio transmitters - into radiant.
Rice. 30. Ways to convert energy from one type to another
The measure of energy is work. The work W performed by an electric current during a time t at a known voltage U and current I is equal to the product of the voltage and the current and the duration of its action:
W=UIt (29)
The work done by an electric current of 1 A at a voltage of 1 V for 1 s is taken as a unit of electrical energy. This unit is called the joule (J). The joule, which is also called the watt-second (W*s), is a very small unit of measurement, so in practice larger units are used to measure electrical energy - watt-hour (1 Wh = 3600 J), kilowatt-hour (1 kW*h = 1000 W*h = 3.6*106 J), megawatt-hour (1 MW*h=1000 kW*h=3.6*109 J).
Electric power. The energy received by the receiver or supplied by the current source within 1 s is called power. Power P at constant values of U and I is equal to the product of voltage U and current I:
P=UI (30)
Using Ohm's law to determine current and voltage as a function of resistance R and conductivity G, other expressions for power can be obtained. If we replace voltage U=IR or current I=U/R=UG in formula (30), we get
P = I2R (31)
or
P = U2/R = U2G (32)
Therefore, electrical power is equal to the square of the current and the resistance, or the square of the voltage divided by the resistance, or the square of the voltage multiplied by the conductivity.
The power that is created by a current of 1 A at a voltage of 1 V is taken as a unit of power and is called a watt (W). In technology, power is measured in larger units: kilowatts (1 kW = 1000 W) and megawatts (1 MW = 1,000,000 W).
Energy losses and efficiency. When converting electrical energy into other types of energy, or vice versa, not all the energy is converted into the required type of energy; part of it is unproductively spent (lost) to overcome friction in machine bearings, heating wires, etc. These energy losses are inevitable in any machine and any apparatus.
The ratio of the power supplied by a source or receiver of electrical energy to the power it receives is called the efficiency of the source or receiver. Efficiency (efficiency)
? = P2/P1 = P2/(P2 + ?P) (33)
Where
P2 — output (useful) power; P1 - received power; ?P - power loss.
Efficiency is always less than unity, since in any machine and any apparatus there are energy losses. Sometimes efficiency is expressed as a percentage. Thus, traction motors of electric and diesel locomotives have an efficiency of 86-92%, powerful transformers - 96-98%, traction substations - 94-96%, contact networks of electrified railways - about 90%, diesel locomotive generators - 92- 94%. Let us consider, as an example, the distribution of energy in an electrical circuit (Fig. 31). Generator 1, powering this circuit, receives mechanical power Pmx = 28.9 kW from prime mover 2 (for example, a diesel engine), and delivers electrical power Rel = 26 kW (2.9 kW is the power loss in the generator). Therefore, it has efficiency ?gen = Rel/Pmx = 26/28.9 = 0.9.
The power Rel = 26 kW supplied by the generator is spent on powering electric lamps (6 kW), heating electric stoves (7.2 kW) and powering the electric motor (10.8 kW). Part of the power ?Ppr = 2 kW is lost to useless heating of the wires connecting the generator to consumers.
Rice. 31. Scheme of energy conversion in an electrical circuit
In each receiver of electrical energy, power losses also occur. In electric motor 3, the power loss is 0.8 kW (it receives 10.8 kW from the network and delivers only 10 kW), so the efficiency ?motor = 10/10.8 = 0.925. Of the 6 kW power received by the lamps, only a small part is used to create radiant energy, most of it is uselessly dissipated as heat. In an electric stove, not all of the 7.2 kW power received is used to heat food, since part of the heat it creates is dissipated in the surrounding space. When considering electrical circuits, along with determining the currents and voltages acting in individual sections, it is also necessary to determine the power transmitted through them. In this case, the so-called energy balance of capacities must be observed. This means that the power received by any device (current source or consumer) or section of the electrical circuit must be equal to the sum of the power it supplies and the power losses that occur in this device or section of the circuit.
Answers
Oersted's experience. Magnetic field of current. Interaction of magnets. The effect of a magnetic field on a current-carrying conductor →
← Series and parallel connections of conductors
Work and power of electric current. Joule-Lenz law
3.1 (62.69%) 119 votes
Current measuring instruments
Electrical measuring instruments are a special type of devices that are used to measure many electrical quantities. These include:
- AC ammeter;
- AC voltmeter;
- Ohmmeter;
- Multimeter;
- Frequency meter;
- Electric meters.
Ammeter
To determine the current strength in an electrical circuit, you need to use an ammeter. This device is connected to the circuit in series and, due to its negligible internal resistance, does not affect its state. The ammeter scale is graduated in amperes.
In a classic device, a measured current passes through an electromagnetic coil, which creates a magnetic field that causes the magnetic needle to deflect. The deflection angle is directly proportional to the measured current.
Classic ammeter
An electrodynamic ammeter has a more complex operating principle. It contains two coils: one is movable, the other stands still. They can be connected to each other in series or in parallel. When current passes through the coils, their magnetic fields begin to interact, which as a result causes the moving coil with an arrow attached to it to deviate by a certain angle proportional to the magnitude of the current being measured.
Voltmeter
A voltmeter is used to determine the voltage (potential difference) across a section of the circuit. The device must be connected parallel to the circuit and have high internal resistance. Then only hundredths of the current will enter the device.
School voltmeter
The principle of operation is that inside the voltmeter there is a coil and a series-connected resistor with a resistance of at least 1 kOhm, on which the volt scale is calibrated. The most interesting thing is that the resistor actually registers the current strength. However, the divisions are selected in such a way that the readings correspond to the voltage value.
Ohmmeter
This device is used to determine electrically active resistance. The principle of operation is to change the measured resistance into a voltage directly dependent on it thanks to an operational amplifier. The desired object must be connected to a feedback circuit or to an amplifier.
You may be interested in Checking a capacitor with a multimeter
If the ohmmeter is electronic, then it will work on the principle of measuring the current flowing through the required resistance at a constant potential difference. All elements are connected in series. In this case, the current strength will have the following dependence: I = U/(r0 + rx), where U is the emf of the source, r0 is the resistance of the ammeter, rx is the desired resistance. According to this dependence, resistance is determined.
Electronic ohmmeter
Multimeter
The devices given as an example are used today only in schools for physics lessons. Multimeters were invented for professional tasks. The most common device includes simultaneously the functions of an ammeter, voltmeter and ohmmeter. The device can be either easily portable or huge stationary with a large number of possibilities. The name “multimeter” was first applied specifically to a digital meter. Analog devices are more often called “avometer”, “tester” or simply “Tseshka”.
Universal multimeter
The work of current is a complex but very important topic in electrodynamics. Without knowing it, you will not be able to solve even the simplest problems. Even electricians use job finding formulas to make the necessary calculations.
Content
In previous lessons, we already mentioned that the electric field has some energy. This means that it is capable of doing some work. This work is called electric current work .
Now let’s remember the definition of mechanical work that we already know. It is determined by the force acting on the body and the distance over which this body moves: $A = Fs$.
If we transfer this knowledge to electrical phenomena, we can say that the work of current is the work of electrical forces that move charged particles in a conductor. But if we use the formula $A = Fs$ for each particle, then subsequent calculations will be incredibly complex. After all, then we will need to know both the exact number of charged particles and the exact distance that they have traveled under the influence of the electric field forces.
We'll go the other way. It will be much simpler and clearer. In this lesson we will define the work of electric current through other electrical quantities (current strength, voltage, electric charge). We will also learn to calculate the work of electric current using the knowledge gained.
Why is it inconvenient to express the work of current in joules in practice?
Let's start with the fact that the passports of electrical appliances usually indicate the current power in them. How can you express the work of a current in terms of power and time?
Knowing the power of the electricity consumer, it is possible to calculate the current work performed in a certain time: $A = Pt$.
Let's consider the units of measurement of quantities in this formula. We measure power in watts , time in seconds , and work in joules .
$1 \space W = 1 \frac{J}{s}$, $1 \space J = 1 \space W \cdot s$.
Please note that time is expressed in seconds. But usually in an electricity consumer the current does work for a longer time.
We use some devices for hours, and some around the clock. For example, the same refrigerator. Electricity is calculated using the meter once a month.
It is logical that it is very inconvenient to convert such large periods of time into seconds each time when calculating the work of electric current. That's why other units of measurement are used.
Non-system units of measurement of electric current work
For the above reasons, when calculating the work of electric current, it is much more convenient to express time in hours. The work itself is often expressed in the following units: $watt \cdot hour$ ($W \cdot hour$), $hectowatt \cdot hour$ ($gW \cdot hour$), $kilowatt \cdot hour$ ($kW \cdot h$).
$1 \space W \cdot h = 3600 \space J$, $1 \space GW \cdot h = 100 \space W \cdot h = 360 \space 000 \space J$, $1 \space kW \cdot h = 1000 \space W \cdot h = 3 \space 600 \space 000 \space J$.