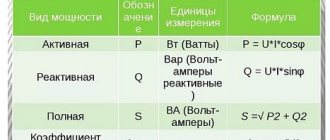
Content
In previous lessons, we already mentioned that the electric field has some energy. This means that it is capable of doing some work. This work is called electric current work .
Now let’s remember the definition of mechanical work that we already know. It is determined by the force acting on the body and the distance over which this body moves: $A = Fs$.
If we transfer this knowledge to electrical phenomena, we can say that the work of current is the work of electrical forces that move charged particles in a conductor. But if we use the formula $A = Fs$ for each particle, then subsequent calculations will be incredibly complex. After all, then we will need to know both the exact number of charged particles and the exact distance that they have traveled under the influence of the electric field forces.
We'll go the other way. It will be much simpler and clearer. In this lesson we will define the work of electric current through other electrical quantities (current strength, voltage, electric charge). We will also learn to calculate the work of electric current using the knowledge gained.
Electric current work and voltage
What is the electrical voltage across the circuit section?
Let us recall the definition of this quantity. We said that the voltage at the ends of the conductor (section of the circuit) is equal to the work that is done when a charge passes through this conductor, equal to $1 \space C$: $U = \frac{A}{q}$.
How can we express the work of electric current in this section through voltage and electric charge passing through a section of a circuit?
Using the electric voltage formula, we express the work of electric current.
$A = Uq$. To determine the work of electric current on any section of the circuit, it is necessary to multiply the voltage at the ends of this section of the circuit by the electric charge (the amount of electricity) passing through it.
Current measuring instruments
Electrical measuring instruments are a special type of devices that are used to measure many electrical quantities. These include:
- AC ammeter;
- AC voltmeter;
- Ohmmeter;
- Multimeter;
- Frequency meter;
- Electric meters.
Ammeter
To determine the current strength in an electrical circuit, you need to use an ammeter. This device is connected to the circuit in series and, due to its negligible internal resistance, does not affect its state. The ammeter scale is graduated in amperes.
In a classic device, a measured current passes through an electromagnetic coil, which creates a magnetic field that causes the magnetic needle to deflect. The deflection angle is directly proportional to the measured current.
Classic ammeter
An electrodynamic ammeter has a more complex operating principle. It contains two coils: one is movable, the other stands still. They can be connected to each other in series or in parallel. When current passes through the coils, their magnetic fields begin to interact, which as a result causes the moving coil with an arrow attached to it to deviate by a certain angle proportional to the magnitude of the current being measured.
Voltmeter
A voltmeter is used to determine the voltage (potential difference) across a section of the circuit. The device must be connected parallel to the circuit and have high internal resistance. Then only hundredths of the current will enter the device.
School voltmeter
The principle of operation is that inside the voltmeter there is a coil and a series-connected resistor with a resistance of at least 1 kOhm, on which the volt scale is calibrated. The most interesting thing is that the resistor actually registers the current strength. However, the divisions are selected in such a way that the readings correspond to the voltage value.
Ohmmeter
This device is used to determine electrically active resistance. The principle of operation is to change the measured resistance into a voltage directly dependent on it thanks to an operational amplifier. The desired object must be connected to a feedback circuit or to an amplifier.
You might be interested in Do-it-yourself generator from an asynchronous motor
If the ohmmeter is electronic, then it will work on the principle of measuring the current flowing through the required resistance at a constant potential difference. All elements are connected in series. In this case, the current strength will have the following dependence: I = U/(r0 + rx), where U is the emf of the source, r0 is the resistance of the ammeter, rx is the desired resistance. According to this dependence, resistance is determined.
Electronic ohmmeter
Multimeter
The devices given as an example are used today only in schools for physics lessons. Multimeters were invented for professional tasks. The most common device includes simultaneously the functions of an ammeter, voltmeter and ohmmeter. The device can be either easily portable or huge stationary with a large number of possibilities. The name “multimeter” was first applied specifically to a digital meter. Analog devices are more often called “avometer”, “tester” or simply “Tseshka”.
Universal multimeter
The work of current is a complex but very important topic in electrodynamics. Without knowing it, you will not be able to solve even the simplest problems. Even electricians use job finding formulas to make the necessary calculations.
Work of electric current and current strength
How to express the work of current in terms of voltage, current and time?
We have already established that the work of electric current can be calculated using the formula: $A = Uq$.
What is the electric charge $q$? Let us recall the definition of current strength: $I = \frac{q}{t}$. Let us express the electric charge from here: $q = It$.
Let's substitute the resulting expression into the formula for calculating the work of electric current: $A = Uq$, $A = UIt$.
The work of an electric current on a section of a circuit is equal to the product of the voltage at the ends of this section by the current strength and the time during which the work was performed: $A = UIt$.
Units of current work
You already know that work is measured in joules ($J$).
Let's see how this unit of measurement compares with others. Voltage is measured in volts ($V$), current in amperes ($A$), and time in seconds ($s$). Then (from the formula $A = UIt$) we can write the following.
$1 \space joule = 1 \space volt \cdot 1 \space ampere \cdot q \space second$, $1 \space J = 1 \space V \cdot A \cdot s$.
Voltage calculation problem
Condition. The electric stove has been plugged in for 20 minutes. What is the voltage in the network if, at a current of 4 A, the work is equal to 480 kJ?
Solution. Since the work and current strength are known, you need to use the following formula: A = U * I * t. Here voltage is an unknown factor. It must be calculated as the quotient of the product and a known factor, that is: U = A /( I * t).
Before making calculations, you need to convert the values to SI units. Namely, work in Joules and time in seconds. This will be 480,000 J and 1200 s. Now all that remains is to count everything.
Answer. The voltage is 100 V.
Measuring current work in practice
What instruments measure the work of electric current?
It turns out that in order to measure the work of electric current, you need to use three devices at once: a voltmeter, an ammeter and a stopwatch.
But there are other special devices - counters (Figure 1).
Figure 1. Electricity meter
In the meter device, the three above-mentioned devices are connected to each other. Such meters are installed in each apartment or in its immediate vicinity (for example, on staircases in apartment buildings).
Sample task
Let's consider an example of a problem to calculate the work of an electric current.
What work does an electric motor do in $1 \space h$ if the current in the electric motor circuit is $5 \space A$ and the voltage at its terminals is $220 \space V$? The engine efficiency is $80\%$.
Let's write down the conditions of the problem and solve it. Don't forget to convert units to SI (hours to seconds).
Given: $t = 1 \space h$ $I = 5 \space A$ $U = 220 \space B$ $\eta = 80 \%$
SI: $t = 3600 \space s$
$A_1 — ?$
Solution:
The total work done by the electric current in the electric motor will be calculated using the formula $A = UIt$. $A = 220 \space B \cdot 5 \space A \cdot 3600 \space c = 3 \space 960 \space 000 \space J$.
Let's remember the definition of efficiency. The efficiency of the mechanism is determined by the ratio of useful work to total work: $\eta = \frac{A_1}{A} \cdot 100 \%$, where $A_1$ is the useful work done by the current in the electric motor.
We have already calculated the total work done by the current. Now let's express the useful work of the engine from the definition of efficiency and calculate it: $A_1 = \frac{A \eta}{100 \%}$, $A_1 = \frac{3 \space 960 \space 000 \space J \cdot 80 \% }{100 \%} = 3 \space 168 \space 000 J \approx 3.2 \cdot 10^6 \space J \approx 3.2 \space MJ$.
Please note that if the problem statement talks about the operation of some electrical device, then we are talking about the useful work of electric current. We can calculate the useful work of electric current using the formula for efficiency, and the total work - using the formulas: $A = Uq$ and $A = UIt$.
Answer: $A_1 \approx 3.2 \space MJ$.
Interpretation of the law of conservation of energy. Joule-Lenz law
Ohm's law for a homogeneous section of a circuit with resistance R is reflected by the formula:
RI=U
Let's multiply both sides of the expression by IΔt and get the relation:
RI2∆t=UI∆t=∆A.
The result obtained is an expression of the law of conservation of energy for a homogeneous section of the chain.
Definition 2
The work ΔA of electric current I flowing through a stationary conductor with resistance R is converted into heat ΔQ released on the conductor.
∆Q=∆A=RI2∆t
This law is called the Joule-Lenz law.
The law bears the name of two famous physicists at once, since it was established experimentally by both of them independently of each other.
Definition 3
The power of the electric current is the ratio of the current work ΔA to the time interval Δt during which this work was performed.
It can be said more simply: power is work done per unit of time. Let us write down the formula connecting the work of the current and its power:
P=∆A∆t=UI=I2R=U2R
The work of an electric current is expressed in joules (J), the current power is measured in watts (W), time is measured in seconds (s): 1 W = 1 J1 s. The current power is measured using a wattmeter, and the work is calculated as a result of multiplying the current strength, voltage and time of current flow through the circuit: A=IUt.
Next, we will analyze a complete direct current circuit, including a source with an electromotive force δ and internal resistance r and an external homogeneous section with resistance R.
Definition 4
Ohm's law for a complete circuit looks like this:
(R+r)I=δ
Do you need help from a teacher? Describe the task - and our experts will help you! Describe the task
Let's multiply both sides of the expression with Δq=IΔt and get a relationship that will serve as an expression of the law of conservation of energy for a complete DC circuit:
RI2∆t+rI2∆t=δI∆t=∆Ast
The left side of the expression contains ΔQ=RI2Δt (heat that is released on the external section of the circuit during the time Δt) and ΔQist=rI2Δt (the heat that is released inside the source during the same time).
The expression δIΔt is equal to the work of external forces ΔAst that act inside the source.
Definition 5
When electric current flows through a closed circuit, the work of external forces ΔAst is converted into heat, which is released in the external circuit (ΔQ) and inside the source (ΔQist).
∆Q+Qist=∆Ast=δI∆t
The following fact should be noted: the work of the electric field is not included in the indicated ratio. When current passes through a closed circuit, the electric field does no work; This means that heat is produced only through external forces that act inside the source. The electric field here redistributes heat between different sections of the circuit.
The external circuit can be not only a conductor with resistance R, but also some device that consumes power, for example, a DC motor. Then R must be regarded as the equivalent load resistance. The energy that is released in the external circuit has the ability to be partially or completely converted into both heat and other types of energy, for example, into mechanical work performed by an electric motor. Thus, the topic of using the energy of a current source is of great practical importance.
It will be interesting➡ Stray currents and ways to deal with them
Exercises
Exercise No. 1
How much work does the electric current do in an electric motor in $30 \space min$ if the current in the circuit is $0.5 \space A$ and the voltage at the motor terminals is $12 \space V$?
Given: $t = 30 \space min$ $I = 0.5 \space A$ $U = 12 \space B$
SI: $t = 1800 \space s$
$A — ?$
Show solution and answer
Hide
Solution:
To calculate the total work of electric current, we use the formula: $A = UIt$.
$A = 12 \space B \cdot 0.5 \space A \cdot 1800 \space c = 10 \space 800 \space J = 10.8 \space kJ$.
Answer: $A = 10.8 \space kJ$.
Exercise No. 2
The voltage on the filament of a flashlight bulb is $3.5 \space V$, the resistance of the filament is $14 \space Ohm$.
How much work does the current do in a light bulb for $5 \space min$? Given: $t = 5 \space min$ $U = 3.5 \space V$ $R = 14 \space Ohm$
SI: $t = 300 \space s$
$A — ?$
Show solution and answer
Hide
Solution: Let's write down the formula for calculating the work of electric current: $A = UIt$.
We can express the unknown current strength through Ohm's law for a section of the circuit: $I = \frac{U}{R}$.
Let's substitute this expression into the formula for calculating the work: $A = U \cdot \frac{U}{R} \cdot t = \frac{U^2 t}{R}$, $A = \frac{3.5^2 \ space В^2 \cdot 300 \space с}{14 \space Ohm} = \frac{3 \space 675 \space В \cdot А \cdot с}{14} = 262.5 \space J$.
Answer: $A = 262.5 \space J$.
Calculation formula
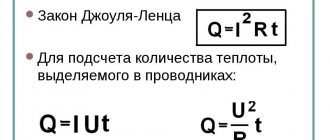
In 1841, the English scientist James Joule formulated a law for finding a quantitative measure of the thermal effect of electric current. In 1842, the same law was also discovered by the Russian physicist Emilius Lenz. Because of this, it received the double name of the Joule-Lenz law. In general, the law is written as follows: Q = I² • R • t.
It is quite general in nature, since it does not depend on the natural forces that generate the current. Today this law is actively applied in everyday life. For example, to determine the degree of heating of the tungsten filament used in light bulbs.
Joule-Lenz law
The Joule-Lenz law determines the amount of heat generated by a current. But, nevertheless, this will help to find out what formulas are used to calculate the work of the electric field. This is because it subsequently manifests itself in the form of heating of the conductor. This suggests that the work done by the current is equal to the heat of heating of the conductor (A=Q). Work of electric current, formula: A= I² • R • t. This is not the only formula for finding a job. If you use Ohm's law for a section of the chain (I=U:R), then you can derive two more formulas: A=I•U•t or A=U²:R.
You might be interested in this Purpose and function of a residual current device (RCD)
Portraits of Joule and Lenz
The general formula for calculating power is that it is directly proportional to work and inversely dependent on time (P=A:t). If we talk about power in an electric field, then based on the previous formulas, we can create as many as three: P = I² • R; P=I•U; Р=U²:R.
Ohm's law for a circuit section