Content
When an electric current passes through a circuit, we can observe its various effects: thermal, chemical, magnetic, light.
Take, for example, the effect of heat. You can confidently say that it can definitely manifest itself to varying degrees . This was confirmed by our experiments. The stretched copper wire simply heated up, but the tungsten coil in the electric lamp certainly heated up more. After all, it became so hot that it began to emit light. This means that we could heat copper wire to a similar state. What needs to be done for this? How to control the current strength? What is this force anyway?
In this lesson you will learn the answers to all these questions. We will look at how charge moves along a conductor when current passes. With the help of this knowledge, we will approach the definition of a new force and its properties - strength .
Current direction
Previously, physicists wrote in textbooks like this: one day they decided that the current was directed from plus to minus, and then they learned that electrons flow through wires. But these electrons are negative, which means they can't do without them. But since we have already agreed on the direction, we will leave it as it is. Then everyone had a question: why can’t the direction of the current be changed? But no one received an answer.
Now they write it a little differently: positive particles flow along the conductor from plus to minus, and the current is directed there. Nobody has any questions here.
| So which version is correct? In fact, both of them. Charge carriers are different for each type of material. In metals these are electrons, in electrolytes they are ions. Each type of particle has its own signs and the need to run to the opposite pole of the charge of the current source. We will not choose the direction of current for each type of material to solve the problem! Therefore, it is customary to direct the current from plus to minus. In most school course assignments, the direction of flow does not play a role, but there is that very insidious minority in which this point will be very important. Therefore, remember: we direct the current from plus to minus. |
Movement of charge along a conductor
As you already know, electric current is the ordered movement of charged particles. We say that particles are “charged” - this means that they have a certain charge $q$.
Accordingly, when such particles move, a certain charge is transferred. Each free electron in a metal carries a charge. Each ion in a solution of acids, salts or alkalis also carries a charge.
It is logical that the more particles move from one section of the chain to another, the greater the total charge they will transfer.
What determines the intensity of the action of electric current? It has been experimentally proven that the intensity (degree of action) of the electric current depends precisely on the magnitude of this transferred charge .
What is the difference between AC and DC current
Current is the movement of charged electrons in a certain direction. This movement is necessary so that household and professional electrical appliances can operate at the installed rated power. In a home outlet, current comes from a power plant, where the kinetic energy of electrons is converted into electrical energy.
You may be interested in the difference between RJ-11 and RJ-12
Constant current is electricity obtained from a phone battery or battery. It is called so because the direction of movement of electrons in it does not change. The operation of chargers is based on this principle: they convert alternating electricity from the network into direct electricity and in this form it accumulates in batteries.
Alternating current is electricity in any home electrical system. It is called so because the direction of electron movement is constantly changing. The number of direction changes is determined by the frequency, which for home networks in the CIS is 50 Hz. This means that in one second the electric current changes direction as many as 50 times. The voltage in the network is the maximum “pressure” that causes electrons to move.
Designation of direct and alternating current
Current strength
The electric charge passing through the cross section of the conductor in $1 \space c$ will determine such a value as the current strength in the circuit (Figure 1).
Figure 1. Charge passing through a cross-section of a conductor
Current strength is a physical quantity equal to the ratio of the electric charge $q$ passing through the cross section of the conductor to the time of its passage $t$: $I = \frac{q}{t}$, where $I$ is the current strength.
Formulas for calculating current characteristics
Lumen is a unit of measurement of luminous flux
If a direct current source is connected to the conductor, the basic parameters can be calculated using the classical formula. Current in amperes is equal to voltage in volts divided by electrical resistance in ohms:
I = U/R.
The power dependence is displayed as follows:
I = P/U = √P/R.
A simple transformation can be used to calculate other quantities:
- R=U/I=U2/P=P/I2;
- U= √P*R=I*R=P/U;
- P=I2*R=U2/I=U*I.
Graphic representation of basic formulas
For your information. In AC circuits, the sinusoidal waveform is taken into account. Resistive loads (capacitors, coils) create a phase shift between voltage and current.
The force of interaction between conductors and current as the basis for determining the unit of current
In order to determine the unit of measurement of current strength, experiments were carried out, which we will now consider. These experiments consisted of the phenomenon of interaction of two conductors with current.
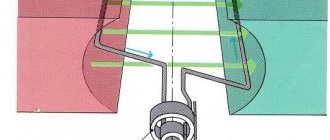
Let's take two flexible straight conductors. Let's place them parallel to each other. Let's connect them to a current source (Figure 2).
Figure 2. Interaction of conductors with current
Once the circuit is closed, an electric current will flow through it. The current will also flow through our experimental conductors.
What will we see? They will begin to interact with each other. Namely, they will be attracted to each other (Figure 2, a) or repelled from each other (Figure 2, b). This will depend on the direction of the current in them.
The question immediately arises of how to measure this force with which the conductors interact? Experiments have shown the following.
The strength of interaction between conductors with current depends on: the length of the conductors; distances between them; the environment in which the conductors are located; current strength in conductors .
For us now the very last point is important. Let's take conductors for which all other conditions will be the same, except for the strength of the currents. It turns out that the greater the current in each conductor, the greater the force they interact with each other.
What do we call a voltage source?
A voltage source, or more precisely a source with a constant output voltage, is a source of electrical energy that has a constant, unchanging voltage at its external terminals, regardless of the current consumed from this source.
Each source has a certain internal resistance and can be represented as a series connection (Fig. 1.12) of an ideal emf, expressed in volts, and a certain internal resistance Rg , expressed in ohms.
Rice. 1.12. Source and external circuit
If an external circuit is connected to such a source, the current consumed by it will flow through the internal resistance of the source. The voltage drop across it is greater, the greater the current consumed by the external circuit. The voltage at the external terminals of the source is equal to the difference between the source emf and the voltage drop across the internal resistance. Therefore, the external voltage can have a constant value, despite changes in current consumption, only when the internal resistance of the source is close to zero. It is this source that we will call a voltage source.
A graphical representation of the voltage source is shown in Fig. 1.13. In practice, ideal constant voltage sources are not found. However, often sources with internal resistance more than 10 times less than the load resistance can be approximately considered voltage sources.
Rice. 1.13 . Graphic representation of voltage source
Current unit
Now imagine very thin and very long conductors. They are located parallel to each other. The distance between them is $1 \space m$. The current strength in them is the same. And all this in a vacuum! This is where the unit of current measurement comes in (Figure 3).
As a unit of current strength, I take the current strength at which segments of parallel conductors of length $1 \space m$ interact with a force of $2 \cdot 10^{-7} \space Н$ ($0.0000002 \space Н$).
Figure 3. Defining the unit of current measurement
The name of this unit is ampere ($A$) . It is named after the French physicist Andre Ampère (Figure 4).
Figure 4. Ampere Andre Marie (1775 - 1836) - French physicist, mathematician and natural scientist. He introduced the concept of electric current into physics, for which he was nicknamed “the Newton of electricity” in the scientific community.
Practical units of electric current work
You all know that at the end of the month you need to pay for the electricity that was used in your apartment. In the SI system, time is measured in seconds, but converting weeks or months into seconds every time is inconvenient and unnecessary. Therefore, people came up with a unit of measurement that is more convenient to use in practice. The energy consumed from the network will depend on the operating time and the power of a particular device. For example, a washing machine will consume more energy in an hour of operation than a light bulb in an entire evening. So, based on the amount of energy consumed, the unit of measurement that is used in practice is the kilowatt hour.
This way you can convert any units of measurement.
There is a cost to using one kilowatt-hour of energy. This cost is multiplied by the number of kilowatt-hours used in a month, and we thus get our electricity bill. For example, 1 kWh costs 3 rubles. Let's say we used 150 kWh of electricity in a month. Then we multiply the number of kilowatt-hours by the cost of one kilowatt-hour and get the amount in rubles.
For example, let’s calculate how much energy an iron will consume in a month if its power is 1800 W and it is used for half an hour every second day.
Since there are 30 days in a month, the iron is used 15 times a month for half an hour. In total, it turns out that the iron works 7.5 hours per month.
Another well-known unit of measurement is horsepower.
. The power of many engines is usually measured in horsepower. If we are talking about the power of electric current, then horsepower is equal to 1 liter. With. = 746 W. For example, we can calculate how much work is done by an 85 hp engine. With. for 2 hours of work. As a rule, the engine does not operate at full power all the time, so we will assume that on average during these 2 hours it worked at 80% power.
The appearance of such units of measurement does not mean that the SI system is somehow bad. On the contrary, the vast majority of calculations should be performed in the SI system, and only then convert the result into any units of measurement. It’s just that SI units are not suitable for some situations.
For example, in astronomy the distances are so large that it is inconvenient to use kilometers: the resulting numbers are huge. For example, from the Sun to the Earth there are almost 150 million km, and to Mercury - about 60 million km. Therefore, scientists decided to introduce a unit of distance known as the astronomical unit (AU). The astronomical unit is the distance between the Sun and the Earth. Thus, the distance from the Sun to Mercury is approximately 0.4 AU. e. Despite this, in astronomy we also talk about distances that are significantly greater than the astronomical unit. In these cases, the light year is used (even though the word "year" is a unit of distance). A light year is the distance that light travels in a vacuum in one year.
For example, the distance from Earth to the center of our galaxy is approximately 26,000 light years.
When making any calculations, you must first make sure that the units of measurement of all quantities correspond to each other. For example, if a car drives at an average speed of 60 km/h, then in 2 hours it will travel 120 km. How did we know this? We multiplied kilometers per hour by hours and got kilometers because the hours were shortened. But if we are given that the speed of the car is 20 m/s, then in order to calculate how far it will travel in 2 hours, we need to convert the hours into seconds, and then just multiply by the speed. Now the resulting distance will be measured in meters, because the speed was given in meters per second.
Current strength of some electrical appliances
For a better understanding of how much one ampere is in practice, Table 1 shows the average current values for some electrical appliances.
| Device | Current value $I$, A |
| Flashlight bulb | 0,1 |
| Regular incandescent lamp | 0,3 — 0,5 |
| Fridge | 0,8 — 1 |
| TV | 1,2 — 2 |
| Electric iron | 3 |
| Vacuum cleaner | 4 — 9 |
| Washing machine | 6 — 10 |
| Trolleybus engine | 160 — 220 |
| Lightning | more than 400,000 |
Table 1. Current values in various electricity consumers
Ammeter
We know where the current is directed, how it is measured, how to calculate it, knowing the charge and the time during which this charge has passed. All that remains is to measure it.
A device for measuring current is called an ammeter. It is connected in an electrical circuit in series with the conductor in which the current is measured.
Ammeters are very different in principle of operation: electromagnetic, magnetoelectric, electrodynamic, thermal and inductive - and these are only the most common.
We will consider only the operating principle of a thermoammeter, because to understand the operating principle of other devices you need to know what a magnetic field and coils are.
The thermoammeter is based on the property of current to heat wires. It works like this: a thin wire is connected to two fixed terminals. This thin thread is held together by a silk thread tied to a spring. Along the way, this wire is wound around a fixed axis on which the arrow is attached. The measured current is supplied to fixed terminals and passed through the wire (arrows in the figure indicate the path of the current).
Under the influence of the current, the thread will heat up slightly, which will lead to stretching, as a result of which the silk thread attached to the thread will be pulled back by a spring. The movement of the wire will rotate the axis, and therefore the arrow. The arrow will show the measurement value.
Relationship between charge unit and current unit
Although we have already talked about charge and its unit of measurement (coulomb) earlier, in physics it is customary to define it in terms of ampere.
Let us express the charge itself from the definition of current ($I = \frac{q}{t}$) and obtain the following formula.
$q = It$.
If $I = 1 \space A$, and $t = 1 \space c$, then we get a unit of electric charge - $1 \space Cl$.
$1 \space pendant = 1 \space ampere \cdot 1 \space s$, or $1 \space Cl = 1 \space A \cdot 1 \space s = 1 \space A \cdot s$.
A unit of electric charge is taken to be the electric charge passing through the cross section of a conductor at a current strength of $1 \space A$ for a time of $1 \space s$.
About electric current
To facilitate understanding of the topic, you can use analogues (comparisons) from the outside world. Electrical quantities are sometimes explained using the example of a conventional pipeline:
- the flow of electrons is similar to the movement of a liquid;
- voltage (potential difference) – different pressure levels;
- as the cross-section of the conductor decreases, the current resistance increases - in the same way, the pressure has to be increased to move more water per unit of time.
Through the transparent walls you can observe the movement of the liquid flow. The presence of visual markers—contaminants—will simplify the visual experiment. However, the most keen-sighted person is not able to see the movement of microscopically small electrons.
However, it is the movement of a stream of charged particles that is an electric current. Why does such an action, even after a long period of experiment, not change the mass (size) of individual sections of the conductor?
As in the case of observation, the answer to the question is explained by the very small magnitude of the parameters under consideration. Electrons can be compared to ants. When moving to another “house”, the old anthill retains its size (shape). Likewise, the mass of the conductor will not change noticeably even if particles with electrical charges are completely removed from it.
Electric charge and its dependence on current and time
We have obtained a formula that allows us to take a fresh look at the definition of electric charge: $q = It$.
We conclude: the electric charge passing through the cross section of the conductor depends on the strength of the current and the time of its passage.
This knowledge will be useful in solving problems. Note that electric charge is sometimes called quantity of electricity .
For example, let's find the amount of electricity that passes through the cross section of the lamp's spiral in $1 \space min$. The lamp current is $400 \space mA$.
Given: $I = 400 \space mA$ $t = 1 \space min$
SI: $I = 0.4 \space A$ $t = 60 \space s$
$q — ?$
Show solution and answer
Hide
Solution:
We use the formula for electric charge obtained from the definition of current: $q = It$.
Let's calculate this charge: $q = 0.4 \space A \cdot 60 \space c = 24 \space Cl$.
Answer: $q = 24 \space Cl$.
Current source
The water in the pipe is taken from the water supply, the spring with water is in the ground - in general, not out of nowhere. Electric current also has its own source.
The source can be, for example, a galvanic cell (ordinary battery). A battery works based on chemical reactions within it. These reactions release energy, which is then transferred to the electrical circuit.
Any source must have poles: “plus” and “minus”. Poles are its extreme positions. Essentially, the terminals to which an electrical circuit is connected. In fact, current simply flows from “+” to “-”.
Exercises
Exercise No. 1
Express in amperes the current equal to $2000 \space mA$;
$100 \space mA$; $55 \space mA$; $3 \space ka$. Given: $I_1 = 2000 \space mA$ $I_2 = 100 \space mA$ $I_3 = 55 \space mA$ $I_4 = 3 \space kA$
Show solution and answer
Hide
Solution:
$I_1 = 2000 \space mA = 2000 \cdot 10^{-3} \space A = 2 \space A$.
$I_2 = 100 \space mA = 100 \cdot 10^{-3} \space A = 0.1 \space A$.
$I_3 = 55 \space mA = 55 \cdot 10^{-3} \space A = 0.055 \space A$.
$I_4 = 3 \space kA = 3 \cdot 10^3 \space A = 3000 \space A$.
Answer: $I_1 = 2 \space A$, $I_2 = 0.1 \space A$, $I_3 = 0.55 \space A$, $I_4 = 3000 \space A$.
Exercise No. 2
The current strength in the electric stove circuit is $1.4 \space A$.
What electric charge passes through the cross section of its spiral in $10 \space min$? Given: $t = 10 \space min$ $I = 1.4 \space A$
SI: $t = 600 \space s$
$q — ?$
Show solution and answer
Hide
Solution:
We use the formula: $q = It$. $q = 1.4 \space A \cdot 600 \space c = 840 \space Cl$.
Answer: $q = 840 \space Kl$.
Examples of Ohm's law calculations
Let's find the voltage if the current is 0.9 Amperes and the resistance is 100 Ohms, using a triangle, cover the voltage with your hand, look, the vertical line means multiply. We use that formula again, just substitute the numbers, U = 0.9 A * 100 Ohm, we think it turns out to be 90, which means U = 90 volts.
Now we calculate the resistance, take the same units, only remove the resistance, we get this formula: R = 90 V \ 0.9 A, we get 100 Ohms.
To calculate the current, we again remove the current, we get this formula I = 90 V \ 100 Ohm, we get 0.9 Amperes. So, that's all, by the way, Ohm's law applies where there are no inductors and capacitors, don't worry about capacitors and inductors, just remember that Ohm's law applies where there are no inductors and capacitors. I hope my article was useful, good luck to everyone, Dmitry Tsyvtsyn was with you.
Current power
Any electrical device (lamp, electric motor, etc.) is designed to consume a certain amount of energy per unit of time. Therefore, along with the work of current, the concept of current power is very important. The current power P is equal to the ratio of the work done by the current A during the time Δt to this time interval:
Using formula (2.7.1), we can give equality (2.7.4) the form:
Formula (2.7.5) is a universal formula for calculating current power. Using Ohm's law, you can obtain two more formulas for current power:
Formulas (2.7.6) and (2.7.7), as well as (2.7.2) and (2.7.3), are suitable only when the work of the current is completely used to increase the internal energy.
The SI unit of work for current is the joule (J) and power is the watt (W). In practice, the off-system unit of current work is widely used - kilowatt-hour (kW • h): 1 kW • h = 3.6 • 106 J.