Мощность электрического тока: определение, формулы, единицы измерения, обозначение

В этой статье мы расскажем вам, что представляет собой мощность электрического тока и как её можно рассчитать.

Определение.

Мощность электрического тока (обозначается буквой P) — это физическая величина, определяемая как количество работы, которая совершается источником электрического напряжения для переноса электрического заряда (q) по проводнику за единицу времени t.

Если сказать в целом, то мощность электрического тока показывает, сколько электрической энергии преобразуется за определенное время. Она, в том числе, описывает энергопотребление потребителя.

Что такое мощность электрического тока

При описании электрической мощности в широком смысле чаще всего речь идет об энергии или силе, которой наделен некоторый объект либо действие. Например, ее можно определить для взрыва или же механизма, например двигателя. Этот параметр связан с силой и зависит от нее, потому эти явления нередко путают.

Отличие в том, что сила влияет на физические действия, то есть выполняется работа. Если она проделана за указанное время, то через эти два параметра можно вычислить значение мощности.

В случае с электричеством она бывает двух видов:

1. Активная – превращается в энергию тепла, света, механических действий и т. д. Она измеряется в ваттах и вычисляется по формуле 1 Вт = 1 В х 1А. Но на практике этот показатель чаще всего выражен в киловаттах и мегаваттах.
2. Реактивная – нагрузка, возникающая из-за колебаний внутри электромагнитного поля. Единица измерения – вольт-амперы (ВА), они вычисляются как Q=U x I x sin угла. Последнее означает изменение фазы между током и снижением напряжения.

На практике отличия обоих видов лучше всего рассмотреть на примере элементов для нагревания и электродвигателей. ТЭНы собраны из материала с высоким сопротивлением, поэтому всю полученную электроэнергию они превращают в тепловую. Электродвигатель же имеет детали, обладающие индуктивностью, то есть часть тока возвращается в сеть и может отрицательно влиять на нее, создавая перегрузки.

Единица измерения мощности

За единицу мощности принимают такую мощность, при которой за 1 с совершается работа в 1 Дж.

Эта единица называется ваттом (Вт) в честь ученого Уатта (рисунок 1).

Из формулы мощности $N = \frac{A}{t}$:

$$1 \space ватт = \frac{1 \space джоуль}{1 \space секунда} = 1 \frac{Дж}{с}$$

Часто используются другие единицы мощности — киловатт (кВт), мегаватт (МВт) и милливатт (мВт):

$1 \space МВт = 1 000 000 \space Вт$

$1 \space Вт = 0.000001 МВт$

$1 \space кВт = 1000 \space Вт$

$1 \space Вт = 0.001 кВт$

$1 \space мВт = 0.001 \space Вт$

$1 \space Вт = 1000 \space мВт$

Также мощность иногда измеряют в лошадиных силах (л. с.):

$1 \space л. с. = 735.5 \space Вт$

$1 \space Вт = 0.00013596 \space л.с.$

Эта единица измерения не так популярна как ватт, но до сих пор используется, например, в автомобильной индустрии.

Как обозначается мощность

Р — мощность электрического тока обозначается (Вт).

В завершение следует отметить, что полная мощность имеет практическое значение, как величина, описывающая нагрузки, фактически налагаемые потребителем на элементы подводящей электросети (провода, кабели, распределительные щиты, трансформаторы, линии электропередачи), так как эти нагрузки зависят от потребляемого тока, а не от фактически использованной потребителем энергии. Именно поэтому данная величина трансформаторов и распределительных щитов измеряется в вольт-амперах, а не в ваттах.

Мощность тока через конденсатор

Пусть на конденсатор подано переменное напряжение . Как мы знаем, ток через конденсатор опережает по фазе напряжение на :

Для мгновенной мощности получаем:

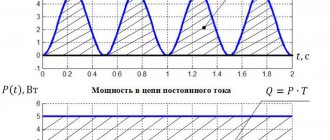
График зависимости мгновенной мощности от времени.

Мощность переменного тока через конденсатор.

Чему равно среднее значение мощности? Оно соответствует «середине» синусоиды и в данном случае равно нулю! Мы видим это сейчас как математический факт. Но интересно было бы с физической точки зрения понять, почему мощность тока через конденсатор оказывается нулевой.

Для этого давайте нарисуем графики напряжения и силы тока в конденсаторе на протяжении одного периода колебаний.

Напряжение на конденсаторе и сила тока через него.

Рассмотрим последовательно все четыре четверти периода.

1. Первая четверть, . Напряжение положительно и возрастает. Ток положителен (течёт в положительном направлении), конденсатор заряжается. По мере увеличения заряда на конденсаторе сила тока убывает.

Мгновенная мощность положительна: конденсатор накапливает энергию, поступающую из внешней цепи. Эта энергия возникает за счёт работы внешнего электрического поля, продвигающего заряды на конденсатор.

2. Вторая четверть, . Напряжение продолжает оставаться положительным, но идёт на убыль. Ток меняет направление и становится отрицательным: конденсатор разряжается против направления внешнего электрического поля.В конце второй четверти конденсатор полностью разряжен.

Мгновенная мощность отрицательна: конденсатор отдаёт энергию. Эта энергия возвращается в цепь: она идёт на совершение работы против электрического поля внешней цепи (конденсатор как бы «продавливает» заряды в направлении, противоположном тому, в котором внешнее поле «хочет» их двигать).

3. Третья четверть, . Внешнее электрическое поле меняет направление: напряжение отрицательно и возрастает по модулю. Сила тока отрицательна: идёт зарядка конденсатора в отрицательном направлении.

Ситуация полностью аналогична первой четверти, только знаки напряжения и тока — противоположные. Мощность положительна: конденсатор вновь накапливает энергию.

4. Четвёртая четверть, . Напряжение отрицательно и убывает по модулю. Конденсатор разряжается против внешнего поля: сила тока положительна.

Мощность отрицательна: конденсатор возвращает энергию в цепь. Ситуация аналогична второй четверти — опять-таки с заменой заменой знаков тока и напряжения на противоположные.

Мы видим, что энергия, забранная конденсатором из внешней цепи в ходе первой четверти периода колебаний, полностью возвращается в цепь в ходе второй четверти. Затем этот процесс повторяется вновь и вновь. Вот почему средняя мощность, потребляемая конденсатором, оказывается нулевой.

Понятие полной мощности. Треугольник мощностей

Полная мощность – это геометрически вычисляемая величина, равная корню из суммы квадратов активной и реактивной мощностей соответственно. Обозначается латинской буквой S.

Также рассчитать полную мощность можно путем перемножения напряжения и силы тока соответственно.

S = U⋅I

ВАЖНО! Полная мощность измеряется в вольт-амперах (ВА).

Треугольник мощностей – это удобное представление всех ранее описанных вычислений и соотношений между активной, реактивной и полной мощностей.

Катеты отражают реактивную и активную составляющие, гипотенуза – полную мощность. Согласно законам геометрии, косинус угла φ равен отношению активной и полной составляющих, то есть он является коэффициентом мощности.

Мощность электрооборудования и неактивная мощность

Паспорта на оборудование содержат активную нагрузку – коэффициент мощности, являющийся важной характеристикой. Она показывает, насколько эффективно бытовой прибор потребляет электроэнергию.

Рис.8

Это число от −1 до 1, оно не бывает равным единице. Коэффициент этот зависит от вида нагрузки: C, L или R. Первые 2 негативно влияют на PF = cos φ системы. Если его параметр большой, ток, потребляемый приборами, увеличивается. Многие силовые нагрузки индуктивные, вынуждают ток отставать от напряжения.

В электрических АС-цепях сетях переменного тока возникает неактивная энергия. Она рассчитывается просто: квадратный корень из суммы (Pa2+Рr2). Если реактивная нагрузка нулевая, то пассивная равняется модулю |Pa|.

Наличие нелинейных искажений тока в электросетях вызвано несоблюдением направления, возникающего между U/I, поскольку энергия обладает импульсным характером. При нелинейных режимах увеличивается полная мощность тока (EP). Подобная нагрузка неактивная, потребляет Pr и энергию искажения тока. Единица измерения – как у обычной мощности Вт.

Как узнать напряжение, зная силу тока

Для расчета напряжения используют формулы:

U=P/I – постоянный ток;

U=P/(I*cos(фи)) — однофазная сеть;

U=P/(1,73*I*cos(фи)) — трехфазная сеть.

Из выражения видно, что напряжение прямо пропорционально напряжению и обратно пропорционально силе тока.

Электрическая мощность: цепь переменного тока

Для таких линий пользоваться формулами, определяющими мгновенные параметры, недопустимо, поскольку итоговый показатель меняется от минимального значения до максимального с частотой сети. Для типовой однофазной сети 220 В характерен синусоидальный сигнал 50 Гц. Разрешается применять простую формулу P = U х I при присоединении приборов, имеющих резистивные параметры:

• ТЭН стиральных машин;
• спирали инфракрасных обогревателей;
• лампочки накаливания.

С помощью этой формулы устанавливается нагрузка.

Как рассчитать мощность, зная силу тока и напряжение

Силовую характеристику электроустановок рассчитывают по формуле:

Советуем к прочтению: Транзисторы и диоды: как работают полупроводники

P=U*I — постоянный ток;

P=U*I*cos(фи) – переменный ток однофазной сети.

P=1,73*U*I*cos(фи) — трехфазная сеть.

В статье приведены упрощенные формулы расчета активной мощности электросети, которые дают приблизительные результаты.

Для получения точных результатов, необходимо учитывать также реактивное и обычное сопротивление, а также потери.

Сила электрического тока через напряжение и ток

Поскольку разница потенциалов, вычисляемая по формуле (F1-F2), определяет напряжение (U), нетрудно сделать вывод о том, что нельзя использовать соотношение, установленное законом Ома. Электрическая мощность (P) также квалифицируется силой тока (I) на конкретном участке линии. Финальное выражение: P = U х I.

Чему равна нагрузка, определяемая через ток и сопротивление

За счет простого преобразования определяется потребление электрической энергии по следующей формуле: P = I2 х R. Здесь показывается зависимость мощности от номинального значения резистора, присоединенного к линии элемента сети. Для полной цепи указываются сопротивление источника (внутреннее) и проводимость точки соединения.

Как правильно рассчитать

Активная мощность, как сделать правильный расчет?

Мощность электрического тока влияет на то, как быстро прибор сможет выполнить работу. К примеру, дорогой обогреватель, имеющий в 2 раза большую мощность, обогреет помещение быстрее, чем два дешевых, с меньшей в 2 раза мощностью. Получается, что выгоднее купить агрегат, имеющий большую мощность, чтобы быстрее обогреть холодное помещение. Но, в то же время, такой агрегат будет тратить существенно больше энергии, чем его более дешевый аналог.

Потребляемая мощность всех приборов в доме учитывается и при подборе проводки для прокладки в доме. Если не учитывать этого и в последующем включить в сеть слишком много приборов, то это вызовет перегрузку сети. Проводка не сможет выдержать мощность электрического тока всех приборов, что приведет к плавлению изоляции, замыканию и самовоспламенению проводки. В результате может начаться пожар, который может привести к непоправимым последствиям.

Однофазный синусоидальный ток в электрических цепях вычисляется по формуле Р = U x I x cos φ, где υ и Ι. Их обозначение шифруется следующим образом: среднеквадратичное значение напряжение и тока, а φ — фазный угол фаз между ними.

Для цепей несинусоидального тока электрическая ёмкость равна корню квадратному из суммы квадратов активной и реактивной производительности. Активная производительность характеризуется скоростью, которая имеет необратимый процесс преобразования электрической энергии в другие виды энергии. Данная ёмкость может вычисляться через силу тока, напряжение и активную составляющую сопротивления цепи r или её проводимость g по формуле P = I(2) x r = U(2) x g.

Следует заметить, что:

• резистор потребляет активную мощность и отдаёт её в форме тепла и света.
• индуктивность потребляет реактивную мощность и отдаёт её в форме магнитного поля.
• конденсатор потребляет реактивную мощность и отдаёт её в форме электрического поля.

В любой электрической цепи как синусоидального, так и несинусоидального тока активная способность всей цепи равна сумме активных мощностей отдельных частей цепи, для трёхфазных цепей электрическая емкость определяется как сумма пропускной способности отдельных фаз. С полной производительностью S, активная связана соотношением P = S x cos φ.

В теории длинных линий (анализ электромагнитных процессов в линии передачи, длина которой сравнима с длиной электромагнитной волны) полным аналогом активной мощности является проходящая мощность, которая определяется как разность между падающей мощностью и отраженной производительностью.

Как найти реактивную полную мощность через активную? Данная производительность, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи синусоидального переменного тока, равна произведению среднеквадратичных значений напряжения U и тока I, умноженному на синус угла сдвига фаз φ между ними: Q = U x I x sin φ (если ток отстаёт от напряжения, сдвиг фаз считается положительным, если опережает — отрицательным).

Пример расчета мощности электрического тока

В конце концов, вы сможете проверить свои познания на 2-ух обычных примерах.

Представьте, что в первой задачке у вас есть резистор R = 50 Ом, через который течет электрический ток I = 0,3А. Какая электрическая мощность преобразуется в этом резисторе?

Вы можете отыскать решение, найдя соответствующую формулу и подставив в нее заданные значения. То есть у нас получается: P = I2R = 0,32 * 50 = 4,5 Вт

Во второй задаче дан резистор R, электрическое сопротивление которого 700 Ом. В техническом описании указано, что максимальная мощность этого резистора составляет 10 Вт. Насколько высоким может быть напряжение, подаваемое на этот резистор?

Для решения этой задачки подбираем подходящую формулу: P = U2/R, откуда мы находим Umax = Pmax * R = 700 * 10 = 83,67 В.

Это означает, что максимальное напряжение может составлять 83,67 В. Чтобы подстраховаться, следует выбирать электрическое напряжение значительно ниже этого предела.

Мощность тока через резистор

Пусть переменный ток протекает через резистор сопротивлением . Напряжение на резисторе, как нам известно, колеблется в фазе с током:

Поэтому для мгновенной мощности получаем:

(2)

Мы видим, что мощность всё время неотрицательна — резистор забирает энергию из цепи, но не возвращает её обратно в цепь.

Мощность переменного тока через резистор.

Максимальное значение нашей мощности связано с амплитудами тока и напряжения привычными формулами:

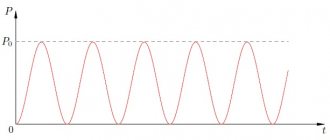
На практике, однако, интерес представляет не максимальная, а средняя мощность тока. Это и понятно. Возьмите, например, обычную лампочку, которая горит у вас дома. По ней течёт ток частотой Гц, т. е. за секунду совершается колебаний силы тока и напряжения. Ясно, что за достаточно продолжительное время на лампочке выделяется некоторая средняя мощность, значение которой находится где-то между и . Где же именно?

Посмотрите ещё раз внимательно на рис. 1. Не возникает ли у вас интуитивное ощущение, что средняя мощность соответствует «середине» нашей синусоиды и принимает поэтому значение ?

Это ощущение совершенно верное! Так оно и есть. Разумеется, можно дать математически строгое определение среднего значения функции (в виде некоторого интеграла) и подтвердить нашу догадку прямым вычислением, но нам это не нужно. Достаточно интуитивного понимания простого и важного факта:

среднее значение квадрата синуса (или косинуса) за период равно .

Среднее значение квадрата синуса равно

Итак, для среднего значения мощности тока на резисторе имеем:

(3)

В связи с этими формулами вводятся так называемые действующие (или эффективные) значения напряжения и силы тока (на самом деле это есть не что иное, как средние квадратические значения напряжения и тока. Такое у нас уже встречалось: средняя квадратическая скорость молекул идеального газа (листок «Уравнение состояния идеального газа»):

(4)

Формулы (3), записанные через действующие значения, полностью аналогичны соответствующим формулам для постоянного тока:

Поэтому если вы возьмёте лампочку, подключите её сначала к источнику постоянного напряжения , а затем к источнику переменного напряжения с таким же действующим значением , то в обоих случаях лампочка будет гореть одинаково ярко.

Действующие значения (4) чрезвычайно важны для практики. Оказывается, вольтметры и амперметры переменного тока показывают именно действующие значения (так уж они устроены). Знайте также, что пресловутые вольт из розетки — это действующее значение напряжения бытовой электросети.

Мощность в механике[ | ]

Если на движущееся тело действует сила, то эта сила совершает работу. Мощность в этом случае равна скалярному произведению вектора силы на вектор скорости, с которой движется тело:

где F {\displaystyle \mathbf {F} } — вектор силы; v {\displaystyle \mathbf {v} } — вектор скорости; α {\displaystyle \alpha } — угол между вектором скорости и силы; F {\displaystyle F} — модуль вектора силы; v {\displaystyle v} — модуль вектора скорости.
Частный случай мощности при вращательном движении:

где M {\displaystyle \mathbf {M} } — момент силы (Н*м); ω {\displaystyle \mathbf {\omega } } — угловая скорость (рад/с); n {\displaystyle n} — частота вращения (число оборотов в минуту, об/мин).

Мощность тока через катушку

Пусть на катушку подано переменное напряжение . Ток через катушку отстаёт по фазе от напряжения на :

Для мгновенной мощности получаем:

Снова средняя мощность оказывается равной нулю. Причины этого, в общем-то, те же, что и в случае с конденсатором. Рассмотрим графики напряжения и силы тока через катушку за период (рис. 5).

Напряжение на катушке и сила тока через неё.

Мы видим, что в течение второй и четвёртой четвертей периода энергия поступает в катушку из внешней цепи. В самом деле, напряжение и сила тока имеют одинаковые знаки, сила тока возрастает по модулю; для создания тока внешнее электрическое поле совершает работу против вихревого электрического поля, и эта работа идёт на увеличение энергии магнитного поля катушки.

В первой и третьей четвертях периода напряжение и сила тока имеют разные знаки: катушка возвращает энергию в цепь. Вихревое электрическое поле, поддерживающее убывающий ток, двигает заряды против внешнего электрического поля и совершает тем самым положительную работу. А за счёт чего совершается эта работа? За счёт энергии, накопленной ранее в катушке.

Таким образом, энергия, запасаемая в катушке за одну четверть периода, полностью возвращается в цепь в ходе следующей четверти. Поэтому средняя мощность, потребляемая катушкой, оказывается равной нулю.