Что такое деформация? Виды деформации
Явление, при котором происходит изменение формы тела под действием какой-либо внешней силы, называется деформацией. Ее природа заключается в движении молекул вещества или целых слоев кристаллической решетки, что приводит к возникновению так называемых дефектов. Степень деформирования зависит от многих факторов, среди которых мы рассмотрим механическое напряжение.
Выделяют несколько видов изменения формы тела:
- Деформация растяжения, когда внешняя сила воздействует вдоль всего тела. Имеет прикладное значение при изготовлении веревок, тросов и строительных материалов;
- Деформация сжатия. В этом случае вектор действия внешней силы совпадает с продольной осью тела, однако он направлен в сторону центра этого тела. Применяется этот вид деформирования при изготовлении металла и строительных материалов для придания им прочности;
- Деформация сдвига возникает под действием внешней силы, которая направлена перпендикулярно продольной оси и вызывает движение различных плоскостей тела относительно друг друга;
- Деформация изгиба характеризуется искривлением главной оси тела, например, когда имеется две точки опоры. Сила, которую может выдержать тот или иной предмет, а также механическое напряжение играют большую роль при создании строительных материалов;
- Деформация кручения возникает при повороте тела вокруг его продольной оси. Этот вид деформации можно наглядно продемонстрировать на пружинке, которая после прекращения воздействия внешней силы восстановит свою форму.
Метод сечений. Напряжения полное, нормальное, касательное
Для расчетов деталей и узлов машин на прочность необходимо знать внутренние силы упругости, возникающие в результате действия приложенных к деталям внешних сил.
Метод сечений широко применяется в сопротивлении материалов для определения внутренних сил, поэтому необходимо рассмотреть его подробно. Всякое тело, в том числе деталь или узел машины, можно представлять как систему материальных точек.
В сопротивлении материалов рассматриваются изменяемые (деформируемые) системы материальных точек.
Метод сечений заключается
в том, что тело мысленно рассекается плоскостью на две части, любая из которых отбрасывается, а взамен нее к сечению оставшейся части прикладываются внутренние силы, действовавшие до разреза. Оставленная часть рассматривается как самостоятельное тело, находящееся в равновесии под действием внешних и приложенных к сечению внутренних сил.
Согласно 3-ему закону Ньютона (аксиома взаимодействия), внутренние силы, действующие в сечении оставшейся и отброшенной частей тела, равны по модулю, но противоположны по направлению. Рассматривая равновесие любой из двух частей рассеченного тела, получаем одно и то же значение внутренних сил, но лучше рассматривать ту часть тела, для которой уравнения равновесия проще.
Согласно допущению о непрерывности материала тела, можно утверждать, что внутренние силы, возникающие в теле, представляют собой силы, равномерно или неравномерно распределенные по сечению.
Применяя к оставленной части тела условия равновесия, можно найти закон распределения внутренних сил по сечению, а также определить статические эквиваленты этих сил.
Основным расчетным объектом в сопротивлении материалов является брус, и нас интересуют внутренние силы в его поперечном сечении, для чего рассмотрим внутренние силы в поперечном сечении бруса.
Рассечем брус (рис. 1.) поперечным сечением а — а
и рассмотрим равновесие его левой части.
Рис. 1.Равновесие левой части бруса.
Если внешние силы, действующие на брус, лежат в одной плоскости, то в общем случае статическим эквивалентом внутренних сил, действующих в сечении а — а,
будут
главный вектор Fm,
приложенный в центре тяжести сечения, и
главный момент МТЛ —
МИ,
уравновешивающие плоскую систему внешних сил, приложенных к оставленной части бруса.
Разложим главный вектор на составляющую N,
направленную вдоль оси бруса, и составляющую
Q,
перпендикулярную этой оси, то есть лежащую в плоскости поперечного сечения. Эти составляющие главного вектора вместе с главным моментом назовем внутренними силовыми факторами, действующими в сечении бруса. Составляющую
N
называют
продольной силой
, составляющую
Q —
поперечной силой
, а пару сил с моментом Мк — изгибающим моментом.
Для определения указанных трех внутренних силовых факторов статика дает три уравнения равновесия оставленной части бруса, а именно:
(ось z
всегда направляем по оси бруса).
Если внешние силы, действующие на брус, не лежат в одной плоскости, то в общем случае в поперечном сечении бруса возникают шесть внутренних силовых факторов (рис. 2), для определения которых статика дает шесть уравнений равновесия оставленной части бруса, а именно:
Рис. 2. 6 внутренних силовых факторов в сечении бруса.
Шесть внутренних силовых факторов, возникающих в поперечном сечении бруса в самом общем случае, носят следующие названия: N —
продольная сила,
Q
x,
Qy—
поперечные силы,
Мк
— крутящий момент,
Мш, Миу—
изгибающие моменты.
При разных деформациях в поперечном сечении бруса возникают различные внутренние силовые факторы. Рассмотрим частные случаи.
1. В сечении возникает только продольная сила N.
В таком случае это деформация растяжения (если сила N направлена от сечения) или деформация сжатия (если сила
N
направлена к сечению).
2. В сечении возникает только поперечная силаQ.
В таком случае это деформация сдвига.
3. В сечении возникает только крутящий моментМк.
В таком случае это деформация кручения.
4. В сечении возникает только изгибающий моментМн.
В таком случае это деформация чистого изгиба. Если в сечении одновременно возникает изгибающий момент
Мн
и поперечная сила
Q,
то изгиб называют поперечным.
5. В сечении одновременно возникает несколько внутренних силовых факторов
(например, изгибающий и крутящий моменты или изгибаюший момент и продольная сила). В этих случаях имеет место сочетание основных деформаций.
Наряду с понятием деформации одним из основных понятий сопротивления материалов является напряжение.
Напряжение характеризует интенсивность внутренних сил, действующих в сечении.
Рассмотрим произвольно нагруженный брус и применим к нему метод сечений (рис. 3). Выделим в сечении малый элемент площади dA ,
считая материал непрерывным. Из- за малости элемента можно считать, что в его пределах внутренние силы, приложенные в различных точках, одинаковы по модулю и направлению и представляют собой систему параллельных сил. Равнодействующую этой системы обозначим
dF.
Разделив
dF
на площадь элементарной площадки
dA,
определим интенсивность внутренних сил, то есть напряжение
р
в точках элементарной площадки
dA
:
Рис. 3.Определение напряжения р по методу сечений.
Таким образом, напряжение есть внутренняя сила, отнесенная к единице площади сечения.
Напряжение есть величина векторная. Единица напряжения:
Эта единица напряжения очень мала, применяют более крупную кратную единицу, а именно мегапаскаль (МПа)
:
1 МПа = 106Па
=
1 Н/мм2
.
Разложим вектор напряжения р
на две составляющие:
Ϭ—
перпендикулярную плоскости сечения и
τ
— лежащую в плоскости сечения (рис. 1.5). Эти составляющие назовем соответственно
нормальным
(
Ϭ
) и
касательным
(
τ
) напряжением.
Так как угол между нормальным и касательным напряжениями всегда равен 90°, то модуль полного напряжения р
определится по формуле
Разложение полного напряжения на нормальное и касательное имеет физический смысл. В поперечном сечении бруса при растяжении, сжатии и чистом изгибе действуют только нормальные напряжения, а при сдвиге и кручении — только касательные напряжения.
Рассмотрим гипотезу, которая носит название принцип независимости действия сил
и формулируется так:
при действии на тело нескольких нагрузок внутренние силы, напряжения, перемещения и деформации в любом месте могут быть определены как сумма этих величин, найденных от каждой нагрузки в отдельности.
Используя принцип независимости действия сил и начав с изучения простейших основных деформаций, когда в поперечных сечениях бруса действуют только нормальные или только касательные напряжения, в дальнейшем перейдем к изучению сложных деформаций, когда в поперечном сечении действуют и те, и другие напряжения, и рассмотрим случаи сочетания деформаций, которые называют сложным сопротивлением.
Хочу отметить, что принцип независимости действия сил применим только для деталей и узлов, деформации которых малы по сравнению с размерами и пропорциональны действующим нагрузкам.
Вопросы для контрольного оценивания
1. В чем заключается метод сечений
2. Какие три внутренних силовых факторы действуют в поперечном сечении бруса?
3. Какой параметр характеризует напряжение?
4. В каких единицах измеряют напряжение?
5. На какие составляющие раскладывают вектор напряжения?
6. Какие напряжения действуют при растяжении, сжатии и чистом изгибе?
7. Сформулируйте принцип независимости действия сил.
Для расчетов деталей и узлов машин на прочность необходимо знать внутренние силы упругости, возникающие в результате действия приложенных к деталям внешних сил.
Метод сечений широко применяется в сопротивлении материалов для определения внутренних сил, поэтому необходимо рассмотреть его подробно. Всякое тело, в том числе деталь или узел машины, можно представлять как систему материальных точек.
В сопротивлении материалов рассматриваются изменяемые (деформируемые) системы материальных точек.
Метод сечений заключается
в том, что тело мысленно рассекается плоскостью на две части, любая из которых отбрасывается, а взамен нее к сечению оставшейся части прикладываются внутренние силы, действовавшие до разреза. Оставленная часть рассматривается как самостоятельное тело, находящееся в равновесии под действием внешних и приложенных к сечению внутренних сил.
Согласно 3-ему закону Ньютона (аксиома взаимодействия), внутренние силы, действующие в сечении оставшейся и отброшенной частей тела, равны по модулю, но противоположны по направлению. Рассматривая равновесие любой из двух частей рассеченного тела, получаем одно и то же значение внутренних сил, но лучше рассматривать ту часть тела, для которой уравнения равновесия проще.
Согласно допущению о непрерывности материала тела, можно утверждать, что внутренние силы, возникающие в теле, представляют собой силы, равномерно или неравномерно распределенные по сечению.
Применяя к оставленной части тела условия равновесия, можно найти закон распределения внутренних сил по сечению, а также определить статические эквиваленты этих сил.
Основным расчетным объектом в сопротивлении материалов является брус, и нас интересуют внутренние силы в его поперечном сечении, для чего рассмотрим внутренние силы в поперечном сечении бруса.
Рассечем брус (рис. 1.) поперечным сечением а — а
и рассмотрим равновесие его левой части.
Рис. 1.Равновесие левой части бруса.
Если внешние силы, действующие на брус, лежат в одной плоскости, то в общем случае статическим эквивалентом внутренних сил, действующих в сечении а — а,
будут
главный вектор Fm,
приложенный в центре тяжести сечения, и
главный момент МТЛ —
МИ,
уравновешивающие плоскую систему внешних сил, приложенных к оставленной части бруса.
Разложим главный вектор на составляющую N,
направленную вдоль оси бруса, и составляющую
Q,
перпендикулярную этой оси, то есть лежащую в плоскости поперечного сечения. Эти составляющие главного вектора вместе с главным моментом назовем внутренними силовыми факторами, действующими в сечении бруса. Составляющую
N
называют
продольной силой
, составляющую
Q —
поперечной силой
, а пару сил с моментом Мк — изгибающим моментом.
Для определения указанных трех внутренних силовых факторов статика дает три уравнения равновесия оставленной части бруса, а именно:
(ось z
всегда направляем по оси бруса).
Если внешние силы, действующие на брус, не лежат в одной плоскости, то в общем случае в поперечном сечении бруса возникают шесть внутренних силовых факторов (рис. 2), для определения которых статика дает шесть уравнений равновесия оставленной части бруса, а именно:
Рис. 2. 6 внутренних силовых факторов в сечении бруса.
Шесть внутренних силовых факторов, возникающих в поперечном сечении бруса в самом общем случае, носят следующие названия: N —
продольная сила,
Q
x,
Qy—
поперечные силы,
Мк
— крутящий момент,
Мш, Миу—
изгибающие моменты.
При разных деформациях в поперечном сечении бруса возникают различные внутренние силовые факторы. Рассмотрим частные случаи.
1. В сечении возникает только продольная сила N.
В таком случае это деформация растяжения (если сила N направлена от сечения) или деформация сжатия (если сила
N
направлена к сечению).
2. В сечении возникает только поперечная силаQ.
В таком случае это деформация сдвига.
3. В сечении возникает только крутящий моментМк.
В таком случае это деформация кручения.
4. В сечении возникает только изгибающий моментМн.
В таком случае это деформация чистого изгиба. Если в сечении одновременно возникает изгибающий момент
Мн
и поперечная сила
Q,
то изгиб называют поперечным.
5. В сечении одновременно возникает несколько внутренних силовых факторов
(например, изгибающий и крутящий моменты или изгибаюший момент и продольная сила). В этих случаях имеет место сочетание основных деформаций.
Наряду с понятием деформации одним из основных понятий сопротивления материалов является напряжение.
Напряжение характеризует интенсивность внутренних сил, действующих в сечении.
Рассмотрим произвольно нагруженный брус и применим к нему метод сечений (рис. 3). Выделим в сечении малый элемент площади dA ,
считая материал непрерывным. Из- за малости элемента можно считать, что в его пределах внутренние силы, приложенные в различных точках, одинаковы по модулю и направлению и представляют собой систему параллельных сил. Равнодействующую этой системы обозначим
dF.
Разделив
dF
на площадь элементарной площадки
dA,
определим интенсивность внутренних сил, то есть напряжение
р
в точках элементарной площадки
dA
:
Рис. 3.Определение напряжения р по методу сечений.
Таким образом, напряжение есть внутренняя сила, отнесенная к единице площади сечения.
Напряжение есть величина векторная. Единица напряжения:
Эта единица напряжения очень мала, применяют более крупную кратную единицу, а именно мегапаскаль (МПа)
:
1 МПа = 106Па
=
1 Н/мм2
.
Разложим вектор напряжения р
на две составляющие:
Ϭ—
перпендикулярную плоскости сечения и
τ
— лежащую в плоскости сечения (рис. 1.5). Эти составляющие назовем соответственно
нормальным
(
Ϭ
) и
касательным
(
τ
) напряжением.
Так как угол между нормальным и касательным напряжениями всегда равен 90°, то модуль полного напряжения р
определится по формуле
Разложение полного напряжения на нормальное и касательное имеет физический смысл. В поперечном сечении бруса при растяжении, сжатии и чистом изгибе действуют только нормальные напряжения, а при сдвиге и кручении — только касательные напряжения.
Рассмотрим гипотезу, которая носит название принцип независимости действия сил
и формулируется так:
при действии на тело нескольких нагрузок внутренние силы, напряжения, перемещения и деформации в любом месте могут быть определены как сумма этих величин, найденных от каждой нагрузки в отдельности.
Используя принцип независимости действия сил и начав с изучения простейших основных деформаций, когда в поперечных сечениях бруса действуют только нормальные или только касательные напряжения, в дальнейшем перейдем к изучению сложных деформаций, когда в поперечном сечении действуют и те, и другие напряжения, и рассмотрим случаи сочетания деформаций, которые называют сложным сопротивлением.
Хочу отметить, что принцип независимости действия сил применим только для деталей и узлов, деформации которых малы по сравнению с размерами и пропорциональны действующим нагрузкам.
Вопросы для контрольного оценивания
1. В чем заключается метод сечений
2. Какие три внутренних силовых факторы действуют в поперечном сечении бруса?
3. Какой параметр характеризует напряжение?
4. В каких единицах измеряют напряжение?
5. На какие составляющие раскладывают вектор напряжения?
6. Какие напряжения действуют при растяжении, сжатии и чистом изгибе?
7. Сформулируйте принцип независимости действия сил.
Упругая и пластическая деформация
Механическое напряжение, которое зависит от природы вещества, влияет на способность тела восстанавливать свою первоначальную форму после возникновения дефекта в кристаллической решетке. По этому признаку выделяют упругую и пластическую деформацию.
При пластической деформации тело после воздействия внешней силы не способно восстановить прежнюю форму. Например, пластилин при надавливании на него пальцем сохраняет образовавшуюся ямку.
Упругая деформация характерна для тех веществ, которые способны восстанавливать свою первоначальную форму после воздействия на них внешней силы. Примером может служить та же пружина, которая при любом описанном выше виде деформации возвращается в первоначальное состояние.
Общие сведения о технологии авиадвигателестроения
Природа предоставляет в распоряжение человека ничтожно малое количество предметов, которые можно использовать непосредственно, без приложения труда человека. Поэтому, человеку приходится почти всегда затрачивать труд, чтобы, путем качественного превращения, приспосабливать предметы природы для удовлетворения своих потребностей.
Качественное изменение предметов природы, осуществляемое человеком, получило название технологического процесса (ТП). Слово «технология» образовано из двух греческих слов: techne – искусство, наука, ремесло и logos – учение, т. о. – учение о ремесле. В настоящее время этому понятию придается значение совокупности знаний о средствах, способах, закономерностях и научных принципах осуществления процессов производства (механической обработки, штамповки, сборки и т. д.), что и составляет предмет изучения курса. Технология машиностроения – это отрасль науки, занимающаяся изучением закономерностей, действующих в процессе изготовления машин, с целью использования этих закономерностей для обеспечения требуемого качества машин и наименьшей себестоимости производства их в установленные сроки.
От того, каким суммарным комплексом технологий владеет государство, зависит эффективность производства в стране в целом, производительность труда во всех отраслях экономики.
Изготовление машин начинается с момента, когда исходным материалам начинают придавать геометрические параметры и физико-механические свойства, требуемые для данной машины, т. е. – с изготовления заготовок её деталей и завершается испытанием машины. В такой широкой области как технология машиностроения находит применение много разных по физической сущности и необходимому оборудованию процессов переработки, обработки и соединения материалов и полуфабрикатов: различные виды литья, обработки давлением, взрывом, резанием, электрохимической обработки, химико-термической обработки, сварки, пайки, сборки, поверхностных покрытий и т. д. Все эти процессы изучаются в учебных дисциплинах, которые по отношению к технологии машиностроения являются базовыми.
Авиадвигателестроение (АДС) – подотрасль авиационной промышленности, обеспечивающая самолеты и вертолеты тяговыми средствами от весовых, ресурсных и экономических характеристик которых зависит эффективность и рентабельность эксплуатации самолетного парка гражданской авиации и тактико-технические данные военной авиации.
АДС относится к среднему точному машиностроению, особенностями которого являются: — Среднее по величине и габаритным размерам изделия. для малоразмерных двигателей наибольший диаметр – 500мм.; для средних двигателей диаметр до 1000мм.; для крупных двигателей транспортных самолетов – 3000мм.; — Высокая точность деталей и изделий. Требования высокой надежности авиационных двигателей и агрегатов в первую очередь связаны с безотказной работой. (Из общего числа отказов самолетов и вертолетов 70% по вине авиадвигателей, а из них 40% по вине агрегатов.) Поэтому требования к точности и качеству обработки касаются не только поверхностей сопряжения, но и свободных поверхностей.
Поверхности сопряжения двигателей находятся на уровне 6-го квалитета, а в агрегатах 5,6-ог квалитета. Точность основных деталей турбин и валов не ниже 8,9-го квалитета.
Шероховатость деталей двигателя в местах сопряжения достигает Ra0,01мкм, а средняя шероховатость Ra2,5мкм. Некоторые детали агрегатов имеют шероховатость Ra0,008мкм.
— Сложность форм и тонкостенность деталей. Удельная масса ГТД в 30, 40 раз меньше чем у автомобильного двигателя. — Широкое использование труднообрабатываемых дорогостоящих материалов. — Большое разнообразие применяемых методов обработки. — Относительно частая смена объектов производства.
Характерные сроки устойчивого производства двигателей: для военной авиации 4…8 лет; для гражданской авиации 10…15 лет. На каждом авиационном заводе выпускается одновременно от 3-5 до 15-20 типов двигателей. Все эти требования обеспечиваются соответственным уровнем организации производственного процесса и качеством разработки и отладки технологического процесса (ТП).
Производственный процесс представляет собой совокупность действий, осуществляемых для превращения материалов и полуфабрикатов в изделие. Производственный процесс охватывает:
- подготовку средств производства;
- организацию обслуживания рабочих мест;
- получение и хранение материалов и полуфабрикатов;
- все стадии изготовления, сборки и испытания изделий;
- транспортировку, технический контроль и реализацию продукции.
ТП является частью производственного процесса, обеспечивающего изготовление деталей.
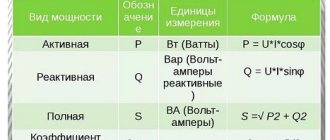
Механическое напряжение: формула и определение
Величина механического напряжения характеризуется внутренними силами молекул, которые направлены против давления и деформации тела, на единицу площади.
Различают два вида напряжения:
- Нормальное напряжение приложено на единицу площади сечения, параллельного главной оси тела.
- Касательное механическое напряжение приложено на единицу площади сечения любой другой плоскости сечения.
Для математического вычисления механического напряжения используется формула: Q=F/S.