Закон Ома для полной электрической цепи. Закон Ома

Определение электрической цепи подразумевает набор некоторых объектов и устройств, между собой соединенных определенным образом, которые являются путем для протекания электрического тока. Физическая величина, характеризующаяся отношением заряда, который сечение проводника за время, к значению этого временного промежутка – это сила тока в цепи.

{ ArticleToC: enabled=yes }

Значение Закона Ома

Закон Ома определяет силу тока в электрической цепи при заданном напряжении и известном сопротивлении. Он позволяет рассчитать тепловые, химические и магнитные действия тока, так как они зависят от силы тока.
Закон Ома является чрезвычайно полезным в технике(электронной/электрической), поскольку он касается трех основных электрических величин: тока, напряжения и сопротивления. Он показывает, как эти три величины являются взаимозависимыми на макроскопическом уровне.

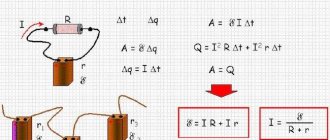
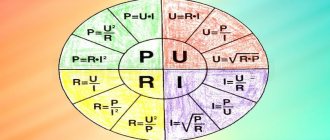
Если бы было можно охарактеризовать закон Ома простыми словами, то наглядно это выглядело бы так:

Из закона Ома вытекает, что замыкать обычную осветительную сеть проводником малого сопротивления опасно. Сила тока окажется настолько большой, что это может иметь тяжелые последствия.

Задача 1.1

Рассчитать силу тока, проходящую по медному проводу длиной 100 м, площадью поперечного сечения 0,5 мм2, если к концам провода приложено напряжение 12 B.

Задачка простая, заключается в нахождении сопротивления медной проволоки с последующим расчетом силы тока по формуле закона Ома для участка цепи. Приступим.

Закон Ома для полной цепи

Формулировка закона Ома для полной цепи – сила тока прямо пропорциональна сумме ЭДС цепи, и обратно пропорциональна сумме сопротивлений источника и цепи , где E – ЭДС, R- сопротивление цепи, r – внутреннее сопротивление источника.

Здесь могут возникнуть вопросы. Например, что такое ЭДС?

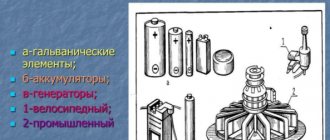
Электродвижущая сила – это физическая величина, которая характеризует работу внешних сил в источнике ЭДС. К примеру, в обычной пальчиковой батарейке, ЭДС является химическая реакция, которая заставляет перемещаться заряды от одного полюса к другому. Само слово электродвижущая говорит о том, что эта сила двигает заряд.

В каждом источнике присутствует внутреннее сопротивление r, оно зависит от параметров самого источника. В цепи также существует сопротивление R, оно зависит от параметров самой цепи.

Формулу закона Ома для полной цепи можно представить в другом виде. А именно: ЭДС источника цепи равна сумме падений напряжения на источнике и на внешней цепи.

Для закрепления материала, решим две задачи на формулу закона Ома для полной цепи.

Задача 2.1

Найти силу тока в цепи, если известно что сопротивление цепи 11 Ом, а источник подключенный к ней имеет ЭДС 12 В и внутреннее сопротивление 1 Ом.

Теперь решим задачу посложнее.

Задача 2.2

Источник ЭДС подключен к резистору сопротивлением 10 Ом с помощью медного провода длиной 1 м и площадью поперечного сечения 1 мм2. Найти силу тока, зная что ЭДС источника равно 12 В, а внутреннее сопротивление 1,9825 Ом.

Приступим.

Несколько примеров

В качестве заключения предлагаем закрепить полученную информацию на нескольких примерах задач, в которых нужно найти силу тока.

1 задача: Рассчитать I в цепи из двух резисторов при последовательном соединении и при параллельном соединении. R резисторов 1 и 2 Ома, источник питания на 12 Вольт.

Из условия ясно, что нужно привести два варианта ответа для каждого из вариантов соединений. Тогда чтобы найти ток при последовательном соединении, сначала складывают сопротивления схемы, чтобы получить общее.

Тогда рассчитать силу тока можно по закону Ома:

При параллельном соединении двух элементов Rобщее можно рассчитать так:

Тогда дальнейшие вычисления можно проводить так:

2 задача: рассчитать ток при смешанном соединении элементов. На выходе источника питания 24В, а резисторы на: R1=1 Ом, R2=3 Ома, R3=3 Ома.

В первую очередь нужно найти R общее параллельно соединенных R2 и R3, по той же формуле, что мы использовали выше.

Теперь схема примет вид:

Далее находим ток по тому же закону Ома:

Теперь вы знаете, как найти силу тока, зная мощность, сопротивление и напряжение. Надеемся, предоставленные формулы и примеры расчетов помогли вам усвоить материал!

Электрическая цепь

Источник электрического тока, соединенный проводами с различными электроприборами и потребителями электрической энергии, образует электрическую цепь.

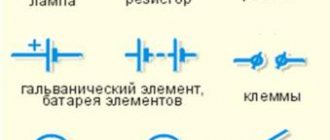
Электрическую цепь принято изображать с помощью схем, в которых элементы электрической цепи (сопротивления, источники тока, включатели, лампы, приборы и т. д.) обозначены специальными значками.

Направление тока в цепи — это направление от положительного полюса источника тока к отрицательному. Это правило было установлено в XIX в. и с тех пор соблюдается. Перемещение реальных зарядов может не совпадать с условным направлением тока. Так, в металлах носителями тока являются отрицательно заряженные электроны, и движутся они от отрицательного полюса к положительному, т. е. в обратном направлении. В электролитах реальное перемещение зарядов может совпадать или быть противоположным направлению тока, в зависимости от того, какие ионы являются носителями заряда — положительные или отрицательные.

Включение элементов в электрическую цепь может быть последовательным или параллельным.

Цепь с активным сопротивлением и индуктивностью

Для цепи, питающейся от переменного тока, в которую включена катушка индуктивности, принято считать, что активное сопротивление ее равняется нулю. В действительности и провод катушки, и соединительные обладают, путь и очень маленьким, активным сопротивлением. Поэтому цепь будет потреблять энергию.

Рекомендуем:

Схемы подключения трехфазного электродвигателя на 220 вольт
Частотный преобразователь для однофазного электродвигателя
Электродвигатели асинхронные трехфазные: технические характеристики, виды, особенности

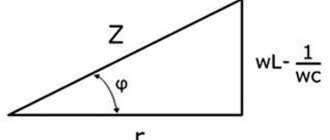
Следовательно, определяя общее сопротивление цепи, учитывать необходимо активное и реактивное сопротивление. Однако, они разнятся по характеру, поэтому обычным способом их складывать невозможно. Использовать нужно метод геометрического сложения, выглядит который следующим образом (рисунок ниже):

Требуется построить треугольник, одна из сторон которого равна величине сопротивления активного, а другая – индуктивного. Величина суммарного сопротивления соответствует третьей стороне, т.е. гипотенузе.

Измеряется полное сопротивление омами, а обозначается «Z». Из выполненного построения понятно, что оно (гипотенуза) больше всегда, чем взятые отдельно величины активного и индуктивного (катетов).

В виде алгебраического выражения это выглядит так:

Здесь:

Z — полное сопротивление;

R — активное;

XL — индуктивное.

Так выглядит зависимость между сопротивлениями составляющих цепь элементов и полным.

Закон Ома для цепи

Закон Ома для участка цепи, безусловно, можно описать известной из школьного курса физики формулой: I=U/R, но некоторые изменения и уточнения внести, думаю, стоит. Возьмем замкнутую электрическую цепь и рассмотрим ее участок между точками 1-2. Для простоты я взял участок электрической цепи, не содержащий источников ЭДС (Е).

Итак, закон Ома для рассматриваемого участка цепи имеет вид:

φ1-φ2=I*R, где

I – ток, протекающий по участку цепи.
R – сопротивление этого участка.
φ1-φ2 – разность потенциалов между точками 1-2.

Если учесть, что разность потенциалов это напряжение, то приходим к производной формулы закона Ома, которая приведена в начале страницы: U=I*R. Это формула закона Ома для пассивного участка цепи (не содержащего источников электроэнергии).

Интересно по теме: Как проверить стабилитрон.

В неразветвленной электрической цепи (рис.2) сила тока во всех участках одинакова, а напряжение на любом участке определяется его сопротивлением:

U1=I*R1
U2=I*R2
Un=I*Rn
U=I*(R1+R2+…+Rn

Отсюда можно получить формулы, которые пригодятся при практических вычислениях. Например:

U=U1+U2+…+Un или U1/U2/…/Un=R1/R2/…/Rn

Расчет сложных (разветвленных) цепей осуществляется с помощью законов Кирхгофа.

Закон Ома для участка цепи.

Для ЭДС

Перед тем как рассмотреть закон Ома для полной (замкнутой) цепи приведу правило знаков для ЭДС, которое гласит:

Если внутри источника ЭДС ток идет от катода (-) к аноду (+) (направление напряженности поля сторонних сил совпадает с направлением тока в цепи, то ЭДС такого источника считается положительной. В противном случае – ЭДС считается отрицательной.

Практическим применением этого правила является возможность приведения нескольких источников ЭДС в цепи к одному с величиной E=E1+E2+…+En, естественно, с учетом знаков, определяемых по вышеприведенному правилу. Например (рис.3.3) E=E1+E2-E3. При отсутствии встречно включенного источника E3 (на практике так почти никогда не бывает) имеем широко распространенное последовательное включение элементов питания, при котором их напряжения суммируются.

Пример 2

Общий ток цепи, содержащей два соединенных параллельно резистора R1=70 Ом и R2=90 Ом, равен 500 мА. Определить токи в каждом из резисторов.

Два последовательно соединенных резистора ничто иное, как делитель тока. Определить токи, протекающие через каждый резистор можно с помощью формулы делителя, при этом напряжение в цепи нам не нужно знать, потребуется лишь общий ток и сопротивления резисторов.

Токи в резисторах

В данном случае удобно проверить задачу с помощью первого закона Кирхгофа, согласно которому сумма токов сходящихся, в узле равна нулю.

Если у вас возникли затруднения, прочтите статью законы Кирхгофа.

Если вы не помните формулу делителя тока, то можно решить задачу другим способом. Для этого необходимо найти напряжение в цепи, которое будет общим для обоих резисторов, так как соединение параллельное. Для того чтобы его найти, нужно сначала рассчитать сопротивление цепи

А затем напряжение

Зная напряжения, найдем токи, протекающие через резисторы

Как видите, токи получились теми же.

Последовательное и параллельное включение элементов

Для элементов электрической цепи (участка цепи) характерным моментом является последовательное либо параллельное соединение. Соответственно, каждый вид соединения сопровождается разным характером течения тока и подводкой напряжения. На этот счёт закон Ома также применяется по-разному, в зависимости от варианта включения элементов.

Цепь последовательно включенных резистивных элементов

Применительно к последовательному соединению (участку цепи с двумя компонентами) используется формулировка:

I = I1= I2 ;
U = U1+ U2 ;
R = R1+ R2

Такая формулировка явно демонстрирует, что, независимо от числа последовательно соединенных резистивных компонентов, ток, текущий на участке цепи, не меняет значения. Величина напряжения, приложенного к действующим резистивным компонентам схемы, является суммой и составляет в целом значение источника ЭДС.

При этом напряжение на каждом отдельном компоненте равно: Ux = I * Rx. Общее сопротивление следует рассматривать как сумму номиналов всех резистивных компонентов цепи.

Цепь параллельно включенных резистивных элементов

На случай, когда имеет место параллельное включение резистивных компонентов, справедливой относительно закона немецкого физика Ома считается формулировка:

I = I1+ I2 … ;
U = U1= U2 … ;
1 / R = 1 / R1+ 1 / R2 + …

Не исключаются варианты составления схемных участков «смешанного» вида, когда используется параллельное и последовательное соединение. Для таких вариантов расчет обычно ведется изначальным расчетом резистивного номинала параллельного соединения. Затем к полученному результату добавляется номинал резистора, включенного последовательно.

Мощность цепи с катушкой индуктивности

Мощность, как известно из программы средней школы, это произведение тока и напряжения, которые являются величинами переменными. Значит, переменной величиной в цепи с активным сопротивлением и индуктивностью будет и мощность.

Ее значение в определенный момент можно вычислить, перемножив значения тока и напряжения в этот же момент. Проделав эти действия для каждого временного момента, получаем графики: а – для содержащей индуктивность цепи, б – активное:

Пунктирной кривой p показана мощность цепи переменного тока, которая состоит из индуктивности. Для ее построения справедливо алгебраическое умножение: умножение двух величин с одинаковым знаком (два минуса или два плюса) в результате дают величину положительную, а при умножении их с разными знаками – отрицательную.

Для цепи, которая помимо индуктивности содержит резистор, график мощности выглядит так:

Линия мощности при этом расположена оси времени. Означает это, что генератор с цепью не обмениваются энергией, поэтому отдаваемая в цепь генератором мощность, цепью потребляется полностью.

Получается, что при большем сдвиге фаз между током и напряжением, меньше мощности, потребляемая цепью.

Сторонняя сила

Тем не менее, ток по цепи идёт; стало быть, имеется сила, «протаскивающая» заряд сквозь источник вопреки противодействию электрического поля клемм (рис. 1).

Рис. 1. Сторонняя сила

Эта сила называется сторонней силой; именно благодаря ей и функционирует источник тока. Сторонняя сила

не имеет отношения к стационарному электрическому полю — у неё, как говорят, неэлектрическое происхождение; в батарейках, например, она возникает благодаря протеканию соответствующих химических реакций.

Обозначим через

работу сторонней силы по перемещению положительного заряда q внутри источника тока от отрицательной клеммы к положительной. Эта работа положительна, так как направление сторонней силы совпадает с направлением перемещения заряда. Работа сторонней силы называется также работой источника тока.

Во внешней цепи сторонняя сила отсутствует, так что работа сторонней силы по перемещению заряда во внешней цепи равна нулю. Поэтому работа сторонней силы по перемещению заряда

вокруг всей цепи сводится к работе по перемещению этого заряда только лишь внутри источника тока. Таким образом, — это также работа сторонней силы по перемещению заряда по всей цепи.

Мы видим, что сторонняя сила является непотенциальной — её работа при перемещении заряда по замкнутому пути не равна нулю. Именно эта непотенциальность и обеспечивает циркулирование электрического тока; потенциальное электрическое поле, как мы уже говорили ранее, не может поддерживать постоянный ток.

Опыт показывает, что работа

прямо пропорциональна перемещаемому заряду . Поэтому отношение уже не зависит от заряда и является количественной характеристикой источника тока. Это отношение обозначается : (1)

Данная величина называется электродвижущей силой (ЭДС) источника тока. Как видим, ЭДС измеряется в вольтах (В), поэтому название «электродвижущая сила» является крайне неудачным. Но оно давно укоренилось, так что приходится смириться.

Когда вы видите надпись на батарейке: «1,5 В», то знайте, что это именно ЭДС. Равна ли эта величина напряжению, которое создаёт батарейка во внешней цепи? Оказывается, нет! Сейчас мы поймём, почему.

КПД электрической цепи

Нетрудно понять, почему резистор

называется полезной нагрузкой. Представьте себе, что это лампочка. Теплота, выделяющаяся на лампочке, является полезной, так как благодаря этой теплоте лампочка выполняет своё предназначение — даёт свет.

Количество теплоты, выделяющееся на полезной нагрузке

за время , обозначим .

Если сила тока в цепи равна

, то

Некоторое количество теплоты выделяется также на источнике тока:

Полное количество теплоты, которое выделяется в цепи, равно:

КПД электрической цепи — это отношение полезного тепла к полному:

КПД цепи равен единице лишь в том случае, если источник тока идеальный

Закон Джоуля-Ленца

Еще одним заданием, которое может ввести в ступор даже более-менее опытного студента – это определить силу тока, если известно время, сопротивление и количество выделенного тепла проводником. Для этого вспомним закон Джоуля-Ленца.

Его формула выглядит так:

Q=I 2 Rt

Тогда расчет проводите так:

I 2 =QRt

Или внесите правую часть уравнения под корень:

I=(Q/Rt) 1/2

Где и когда можно применять закон Ома?

Закон Ома в упомянутой форме справедлив в достаточно широких пределах для металлов. Он выполняется до тех пор, пока металл не начнет плавиться. Менее широкий диапазон применения у растворов (расплавов) электролитов и в сильно ионизированных газах (плазме).

Работая с электрическими схемами, иногда требуется определять падение напряжения на определенном элементе. Если это будет резистор с известной величиной сопротивления (она проставляется на корпусе), а также известен проходящий через него ток, узнать напряжение можно с помощью формулы Ома, не подключая вольтметр.

Источники

https://toe.1c-umi.ru/lekcii/lekciya_6_-_zakon_oma/
https://www.calc.ru/Zakon-Oma-Dlya-Polnoy-Elektricheskoy-Tsepi.html
https://ElectroInfo.net/teorija/vse-o-zakone-oma-prostymi-slovami-s-primerami-dlja-chajnikov.html
https://ege-study.ru/ru/ege/materialy/fizika/eds-zakon-oma-dlya-polnoj-cepi/
https://OFaze.ru/teoriya/zakona-oma-dlya-polnoj-tsepi

Метод контурных токов

Рассмотренный выше метод расчета электрических цепей при анализе больших и разветвленных цепей приводит к неоправданно трудоемким расчетам, поэтому редко применяется. Более широко используется метод контурных токов, позволяющий значительно сократить количество уравнений. При этом вместо токов в ветвях электрической цепи определяются так называемые контурные токи при помощи второго закона Кирхгофа. Таким образом, количество требуемых уравнений будет равняться числу независимых контуров. В качестве примера рассчитаем цепь изображённую на рисунке ниже

Если бы мы вели расчёт цепи по методу законов Ома и Кирхгофа, то необходимо было бы решить систему из пяти уравнений. Для расчёта по методу контурных токов необходимо всего три уравнения.

В начале расчёта выделяют независимые контуры, в нашем случае это: E1R1R2E2, E2R2R4E3R3 и E3R4R5. Затем контурам присваивают произвольно направленный контурный ток, который имеет одинаковое направление для всех участков выбранного контура, в нашем случае для первого контура контурный ток будет Ia, для второго – Ib, для третьего – Ic. Как видно из рисунка некоторые контурные токи соответствуют токам в ветвях

Остальные же токи можно найти как разность двух контурных токов

В результате выбора контурных токов можно составить систему уравнений по второму закону Кирхгофа

Рассчитаем схему, изображённую на рисунке выше со следующими параметрами E1 = E3 = 100 B, E2 = 50 B, R1 = R2 = 10 Ом, R3 = R4 = R5 = 20 Ом. Запишем систему уравнений

В результате решения системы получим Ia = I1 = 4,286 А, Ib = I3 = 3,571 А, Ic = I5 = -0,714 А, I2 = -0,715 А, I4 = 4,285 А. Так же как и в предыдущем случае если токи получаются отрицательными, значит действительное направление противоположно принятому. Таким образом, токи I2 и I5 имеют направление противоположное изображённым на рисунке.