Сила Лоренца просто и понятно: определение, формула, правило левой руки

Определение

В узком понимании, правило буравчика – это мнемонический алгоритм, применяемый для определения пространственного направления магнитной индукции, в зависимости от ориентации электрического тока, возбуждающего магнитное поле.

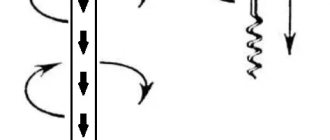
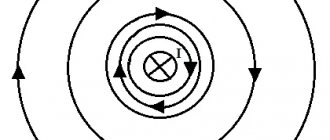
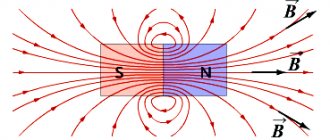
Данное правило можно сформулировать следующим образом: Если острие буравчика (штопора, винта) направить вдоль вектора тока, то ориентация линий магнитной индукции совпадёт с направлением, в сторону которого вращается ручка буравчика в традиционном исполнении этого инструмента (с правым винтом) [ ] (рис. 1.)

На рисунке 1 показана схема для простейшего случая: по прямому участку проводника, в сторону от наблюдателя протекает электрический ток (стрелка синего цвета). Условный штопор направлен своим острым концом по вдоль линии по направлению тока. Если представить поступательное движение буравчика вдоль проводника, то направление линий, описываемых рукояткой штопора, совпадут с ориентацией магнитных линий электрического поля.

Примеры задач в физике электротехнике

В качестве примеров будут рассмотрены задачи, связанные с силой Ампера. Примеры решений специфические, но сам метод решения довольно простой.

Задача № 1

Исходные данные для выполнения: длина проводника – 20 см, сила тока, протекающая в нем – 300 мА, угол между проводником и вектором магнитной индукции – 45о. Величина магнитной индукции – 0,5 Тл.

Требуется найти силу однородного магнитного поля, воздействующую на проводник.

Решение: необходимо применять основную формулу – Fa = B x I x L x sinα. Подставив нужные значения, получаем: Fa = 0,5 Тл х 0,3А х 0,2 м х (√2/2) = 0,03 Н.

Задача № 2

Исходные данные для решения: Проводник помещен в магнитное поле, индукция которого составляет 10 Тл. Сила действия магнитного поля перпендикулярна проводнику и составляет 20 Н. Сила тока, протекающего в проводнике – 5А.

Требуется вычислить длину отрезка проводника.

Решение: за основу берется формула Fa = B x I x L x sinα. Длина проводника определяется следующим образом: L = Fa/(B x I x sinα). Поскольку sinα = 1, получаем: L = Fa/(B x I). Остается подставить нужные значения и получить результат: L = 20Н/(10Тл х 5А) = 0,4 м.

Существуют аналогичные задачи с использованием силы Лоренца. Наглядно рассматрим два примера, которые решаются просто и понятно.

Задача № 3

Исходные данные для выполнения: в магнитном поле с индукцией 0,3 Тл передвигается заряд величиной 0,005 Кл со скоростью 200 м/с. Угол между направлением заряда и вектором магнитной индукции – 45º.

Определяется: величина силы, воздействующей на заряд.

Решение: используется основная формула FL = |q| x V x B x sinα. Подставляя исходные данные, получаем следующее: FL = 0,005Кл х 200м/с х 0,3Тл х sin 45о = (0,3 х √2)/2 = 0,21Н.

Задача № 4

Исходные данные для решения: заряженная частица величиной 0,5 мКл движется в магнитном поле с индукцией 2 Тл. Сила, действующая на заряд со стороны магнитного поля – 32 Н. Направление движения частицы и вектор магнитного поля расположены под углом 90º.

Требуется определить: скорость движения заряженной частицы.

Решение: изначально берется формула FL = |q| x V x B x sinα. Поскольку sinα = 1, она приобретает следующий вид: FL = |q| x V x B. Для определения скорости нужно: V = FL/(|q| x B). Остается вставить исходные данные: V = 32Н/(5*10-4Кл х 2Тл) = 32000 м/с.

Главное правило

Рассмотренный нами пример является частным случаем алгоритма буравчика. Существует несколько вариантов формулировок правила, применяемых в различных ситуациях.

Общая, или главная формулировка, позволяет распространить данное правило на все случаи. Это вариант мнемонического правила, используемый для определения ориентации результирующей векторного произведения, называемого аксиальным вектором, а также для выбора связанного с этими векторами правого базиса (трёхмерной системы координат), что позволяет определить знак аксиального вектора.

Примечание: правый базис – условное соглашение, согласно которому выбирается декартовая система координат (положительный базис). Иногда полезно пользоваться зеркальным отражением декартовой системы (левый или отрицательный базис).

Главное правило позволяет определить направление в пространстве аксиальных векторов, важных для вычислений:

• угловой скорости;
• параметров индукционного тока;
• магнитной индукции.

Хотя ориентация аксиального вектора является условной, она важна для расчётов: придерживаясь принятого алгоритма выбора, легче производить вычисления, без риска перепутать знаки.

Во многих случаях применяют специальные формулировки, хорошо описывающие частные случаи в конкретной ситуации.

Видео

И в завершение небольшой видео урок о силе Ампера.

Автор: Павел Чайка, главный редактор журнала Познавайка

При написании статьи старался сделать ее максимально интересной, полезной и качественной. Буду благодарен за любую обратную связь и конструктивную критику в виде комментариев к статье. Также Ваше пожелание/вопрос/предложение можете написать на мою почту [email protected] или в Фейсбук, с уважением автор.

Страница про автора

Правило правой руки

В электротехнике очень часто применяют интерпретацию буравчика для правой руки.

Действия можно сформулировать так: «Если отведённый в сторону большой палец правой руки расположить вдоль проводника так, чтобы он совпал с направлением электрического тока, то остальные пальцы будут указывать направление образованных электрическим полем магнитных силовых линий. (см. схему на рис. 2).

Сформулированные выше алгоритмы применяются и для соленоидов. Но разница в том, что в случае с соленоидом, рукоятку буравчика вращают так, чтобы это движение совпадало с направлением токов в витках, а продвижение винта буравчика указывает на ориентацию вектора магнитных линий в соленоиде.

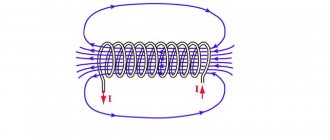
При использовании правой руки, пальцами охватывают (условно) катушку так, чтобы направление тока в витках совпадало с пространственным расположением пальцев. Тогда большой палец укажет на ориентацию вектора электромагнитных линий внутри катушки. На рисунке 3 изображены схемы, объясняющие алгоритмы определения направлений векторов для соленоидов.

Не трудно догадаться, что данные правила можно применять с целью определения направления тока. Например, если с помощью магнитной стрелки определить устремление линий магнитной индукции, то путём применения правила буравчика (как вариант его формулировки для правой руки), легко определяется, в какую сторону течёт ток.

Немного истории

Первые попытки описать электромагнитную силу были сделаны еще в XVIII веке. Ученые Генри Кавендиш и Тобиас Майер высказали предположение, что сила на магнитных полюсах и электрически заряженных объектах подчиняется закону обратных квадратов. Однако экспериментальное доказательство этого факта не было полным и убедительным. Только в 1784 году Шарль Августин де Кулон при помощи своего торсионного баланса смог окончательно доказать это предположение.

В 1820 году физиком Эрстедом был открыт факт, что на магнитную стрелку компаса действует ток вольта, а Андре-Мари Ампер в этом же году смог разработать формулу угловой зависимости между двумя токовыми элементами. По сути, эти открытия стали фундаментом современной концепции электрических и магнитных полей. Сама же концепция получила свое дальнейшее развитие в теориях Майкла Фарадея, особенно в его представлении о силовых линиях. Лорд Кельвин и Джеймс Максвелл дополнили теории Фарадея подробным математическим описанием. В частности Максвеллом было создано так званное, «уравнение поля Максвелла» – представляющее собой систему дифференциальных и интегральных уравнений, описывающих электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и сплошных средах.

Джей Джей Томпсон был первым физиком, кто попытался вывести из уравнения поля Максвелла электромагнитную силу, которые действует на движущийся заряженный объект. В 1881 году он опубликовал свою формулу F = q/2 v x B. Но из-за некоторых просчетов и неполного описания тока смещения она оказалась не совсем правильной.

И вот, наконец, в 1895 году голландский ученый Хендрик Лоренц вывел правильную формулу, которая используется и поныне, а также носит его имя, как и та сила, что действует на летящую частицу в магнитном поле, отныне называется «силой Лоренца».

Специальные правила

Рассмотрим варианты главного правила буравчика для частных случаев. Применение таких правил часто упрощает процесс вычислений.

Для векторного произведения

Расположите векторы так, чтобы их начальные точки совпадали. Для этой ситуации правило буравчика звучит так:

Если один из векторов сомножителей вращать кратчайшим способом до совпадения направлений со вторым вектором, то буравчик, вращающийся подобным образом, будет завинчиваться в сторону, куда указывает векторное произведение.

По циферблату часов

При расположении векторов способом совпадения их начальных точек можно определить направление вектора-произведения с помощью часовой стрелки. Для этого необходимо мысленно двигать кратчайшим путём один из векторов-сомножителей в сторону другого вектора. Тогда, если смотреть со стороны вращения этого вектора по часовой стрелке, то аксиальный вектор будет направлен вглубь циферблата.

Правила правой руки, для произведения векторов

Существует два варианта правила.

Первый вариант:

Если согнутые пальцы правой руки направить в сторону кратчайшего пути для совмещения вектора-сомножителя с другим сомножителем (векторы выходят из одной точки), то отведенный в сторону большой палец укажет направление аксиального вектора.

Второй вариант:

Если правую ладонь расположить таким образом, чтобы получилось совпадение большого пальца с первым вектором-сомножителем, а указательного – со вторым, то отведённый в сторону средний палец совпадёт с направлением вектора произведения.

Для базисов

Перечисленные выше правила применяются также для базисов.

Например, правило буравчика для правого базиса можно записать так:

При вращении ручки буравчика и векторов таким образом, чтобы первый базисный вектор по кратчайшему пути стремился ко второму, то штопор будет завинчиваться в сторону третьего базисного вектора.

Указанные правила универсальны. Их можно переписать для механики с целью определения векторов:

• механического вращения (определение угловой скорости);
• момента приложенных сил;
• момента импульса.

Правила буравчика применяются также для уравнений Максвелла, что усиливает их универсальность.

Практическое применение

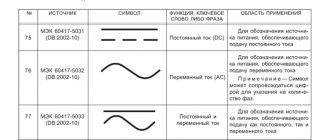
Применение силы Ампера в современном мире очень широкое, можно даже без преувеличение сказать, что мы буквально окружены силой Ампера. Например, когда вы едете в трамвае, троллейбусе, электромобиле, его в движение приводит именно она, сила Ампера. Аналогичны лифты, электрические ворота, двери, любые электроприборы, все это работает именно благодаря силе Ампера.

Правило левой руки

В электротехнике довольно часто возникают вопросы, связанные с определением силы Ампера. Для решения задач подобного рода применяется алгоритм, называемый правилом левой руки (иллюстрация на рис. 4) – мнемоническое правило, описывающее способ определения направленности Амперовой силы, выталкивающей точечный заряд либо проводник, по которому протекает электроток.

Алгоритм применения левой руки состоит в следующем: если левую ладонь будут перпендикулярно пронизывать силовые линии, а пальцы расположатся по направлению тока, то действующие на проводник силы будут устремляться в сторону, куда указывает оттопыренный большой палец.

Интерпретация для точечного заряда

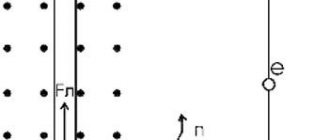
Заметим, что сформулированное правило справедливо для решения задач по определению ориентации силы Лоренца. Перефразируем правило: если ладонь левой руки поместить в магнитное поле таким образом, чтобы линии индукции перпендикулярно входили в неё, а выпрямленные пальцы направить в сторону движения положительного заряда, тонаправление вектора силы Лоренца совпадёт с отставленным на 90º большим пальцем.

Визуальная интерпретация правила левой руки представлена на рисунке 5. Обратите внимание на то, что алгоритм действий для определения сил Ампера и Лоренца практически одинаков.

Примечание: В случае с отрицательным зарядом вытянутые пальцы направляют в сторону, противоположную движению частицы.

Что такое сила Лоренца — определение, когда возникает, получение формулы

Известно, что электрический ток – это упорядоченное перемещение заряженных частиц. Установлено также, что во время движения в магнитном поле каждая из этих частиц подвергается действию силы. Для возникновении силы требуется, чтобы частица находилась в движении.
Сила Лоренца – это сила, которая действует на электрически заряженную частицу при её движении в магнитном поле. Её направление ортогонально плоскости, в которой лежат векторы скорости частицы и напряженности магнитного поля. Равнодействующая сил Лоренца и есть сила Ампера. Зная ее, можно вывести формулу для силы Лоренца.

Время, требуемое для прохождения частицей отрезка проводника,

, где – длина отрезка, – скорость частицы. Суммарный заряд, перенесенный за это время через поперечное сечение проводника,

Подставив сюда значение времени из предыдущего равенства, имеем

(2)

В то же время , где – количество частиц, находящееся в рассматриваемом проводнике. При этом , где – заряд одной частицы. Подставив в формулу значение из (2), можно получить:

Таким образом,

Используя (1), предыдущее выражение можно записать как

После сокращений и переносов появляется формула для вычисления силы Лоренца

С учетом того, что формула записана для модуля силы, ее необходимо записать так:

(3)

Поскольку , то для вычисления модуля силы Лоренца неважно, куда направлена скорость, – по направлению силы тока или против, – и можно сказать, что – это угол, образуемый векторами скорости частицы и магнитной индукции.

Запись формулы в векторном виде будет выглядеть следующим образом:

– это векторное произведение, результатом которого является вектор с модулем, равным Исходя из формулы (3), можно сделать вывод о том, что сила Лоренца является максимальной в случае перпендикулярности направлений электрического тока и магнитного поля, то есть при , и исчезать при их параллельности (

Необходимо помнить, что для получения правильного количественного ответа – например, при решении задач, – следует пользоваться единицами системы СИ, в которой магнитная индукция измеряется в теслах (1 Тл = 1 кг·с−2·А−1), сила – в ньютонах (1 Н = 1 кг·м/с2), сила тока – в амперах, заряд в кулонах (1 Кл = 1 А·с), длина – в метрах, скорость – в м/с.

Полезные сведения и советы

1. Общепринято считать, что направление тока указывает в сторону от плюса к минусу. На самом деле, в проводнике упорядоченное перемещение электронов направлено от негативного полюса к позитивному. Поэтому, если бы перед вами стояла задача вычисления силы Лоренца для отдельного электрона в проводнике, следовало бы учитывать данное обстоятельство.
2. По умолчанию мы рассматриваем винт (буравчик, штопор) с правой резьбой. Однако не следует забывать о существовании винтов с левой резьбой.
3. При использовании правила часовой стрелки мы принимаем условие о том, что стрелки совершают движение слева направо. Известно, что в бывшем СССР производились часы с обратным ходом часового механизма. Возможно, такие модели существуют до сегодняшнего дня.

Советы: если вам необходимо определить пространственное расположение момента силы, под действием которой происходит вращение некоего тела – вращайте винт в ту же сторону. Условное врезание винта укажет на ориентацию вектора момента силы. Скорость вращения тела не влияет на направление вектора.

Полезно знать, что при вращении буравчика по ходу вращения тела, траектория его ввинчивания совпадёт с направлением угловой скорости.

Магнитное поле в соленоиде

Законы правой и левой руки в физике, разобранные ранее, на сто процентов действуют лишь для прямолинейных токопроводников. Однако, довольно часто провода используются в виде катушек или соленоидов, где все процессы происходят по-другому.

Известно, что под влиянием электротока, проходящего внутри провода, образуется круговое магнитное поле. В катушечных соленоидах провод сворачивается в виде колец и многократно оборачивается вокруг сердечника. Здесь правило Буравчика в чистом виде уже не функционирует, поскольку происходит существенное усиление магнетических полей. Но, его условные линии направлены так же, как и у постоянных магнитов, поэтому в таком случае возможно применение правила правой руки.

Сначала соленоид охватывается так, чтобы самый крупный палец смотрел в направлении северного магнитного полюса. Он же отображает направление вектора магнитной индукции. Остальные четыре пальчика располагаются в направлении протекания тока.

Возможно частично применить и правило штопора. Его следует установить и закручивать в направлении тока, тогда острие станет перемещаться в направлении электромагнитной индукции. Эта установка действует не только для всей катушки, но и для одиночного витка.