Определение Сила Лоренца — сила, действующая на движущуюся заряженную частицу со стороны магнитного поля.
Модуль силы Лоренца обозначается как FЛ. Единица измерения — Ньютон (Н).
Модуль силы Лоренца численно равен отношению модуля силы F, действующий на участок проводника длиной l, к числу N заряженных частиц, упорядоченно движущихся на этом участке проводника:
FЛ=FN.
Рассмотрим отрезок тонкого прямого проводника с током. Пусть длина отрезка ∆l и площадь поперечного сечения проводника S настолько малы, что вектор индукции магнитного поля →B можно считать неизменным в пределах этого отрезка проводника.
Сила тока I в проводнике связана с зарядом частиц q, концентрацией заряженных частиц (число зарядов в единице объема) и скоростью их упорядоченного движения v следующей формулой:
I=qnvS
Модуль силы, действующей со стороны магнитного поля на выбранные элемент тока, равен:
F=|I|ΔlBsin.α
Подставляя сюда выражение, полученное для силы тока, получим:
F=|qnvS|ΔlBsin.α=|q|nvSΔlBsin.α
Учтем, что число заряженных частиц в рассматриваемом объеме равно произведению величины этого объема на концентрацию самих частиц:
N=nSΔlB
Тогда:
F=|q|vNBsin.α
Следовательно, на каждый движущийся заряд действует сила Лоренца, равная:
FЛ=FN..=|q|vNBsin.αN..=|q|vBsin.α
α — угол между вектором скорости движущегося заряда и вектором магнитной индукции.
Пример №1. Определить силу, действующую на заряд 0,005 Кл, движущийся в магнитном поле с индукцией 0,3 Тл со скоростью 200 м/с под углом 45o к вектору магнитной индукции.
FЛ=|q|vBsin.α=0,005·200·0,3·√22..≈0,2 (Н)
Определение и формула силы Лоренца
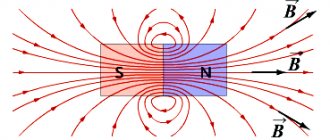
В школе очень часто показывают опыт с магнитом и железными опилками на бумажном листе. Если расположить его под бумагой и слегка потрясти, то опилки выстроятся по линиям, которые принято называть линиями магнитной напряженности. Говоря простыми словами, это силовое поле магнита, которое окружает его подобно кокону. Оно замкнуто само на себя, то есть не имеет ни начала, ни конца. Это векторная величина, которая направлена от южного полюса магнита к северному.
Если бы в него влетела заряженная частица, то поле воздействовало бы на него очень любопытным образом. Она бы не затормозилась и не ускорилась, а всего лишь отклонилась в сторону. Чем она быстрее и чем сильнее поле, тем больше на нее действует эта сила. Ее назвали силой Лоренца в честь ученого-физика, впервые открывшего это свойство магнитного поля.
Вычисляют ее по специальной формуле:
FЛ=qvB,
здесь q – величина заряда в Кулонах, v – скорость, с которой движется заряд, в м/с, а B – индукция магнитного поля в единице измерения Тл (Тесла).
Полезные сведения и советы
- Общепринято считать, что направление тока указывает в сторону от плюса к минусу. На самом деле, в проводнике упорядоченное перемещение электронов направлено от негативного полюса к позитивному. Поэтому, если бы перед вами стояла задача вычисления силы Лоренца для отдельного электрона в проводнике, следовало бы учитывать данное обстоятельство.
- По умолчанию мы рассматриваем винт (буравчик, штопор) с правой резьбой. Однако не следует забывать о существовании винтов с левой резьбой.
- При использовании правила часовой стрелки мы принимаем условие о том, что стрелки совершают движение слева направо. Известно, что в бывшем СССР производились часы с обратным ходом часового механизма. Возможно, такие модели существуют до сегодняшнего дня.
Полезно знать, что при вращении буравчика по ходу вращения тела, траектория его ввинчивания совпадёт с направлением угловой скорости.
- https://odinelectric.ru/knowledgebase/sila-lorenca-i-pravilo-levoj-ruki-dvizhenie-zarjazhennyh-chastic-v-magnitnom-pole
- https://intech-irk.ru/tehnika/pravilo-pravoj-ruki.html
- https://www.asutpp.ru/pravilo-buravchika-prostym-yazykom.html
- https://electric-220.ru/pravilo-levoj-ruki
- https://seti.guru/pravilo-pravoy-i-levoy-ruki-v-fizike-primenenie
Направление силы Лоренца
Ученые заметили, что есть определенная закономерность между тем, как частица влетает в магнитное поле и тем, куда оно ее отклоняет. Чтобы ее было легче запомнить, они разработали специальное мнемоническое правило. Для его запоминания нужно совсем немного усилий, ведь в нем используется то, что всегда под рукой – рука. Точнее, левая ладонь, в честь чего оно носит название правила левой руки.
Итак, ладонь должна быть раскрыта, четыре пальца смотрят вперед, большой палец оттопырен в сторону. Угол между ними составляет 900. Теперь необходимо представить, что магнитный поток представляет собой стрелу, которая впивается в ладонь с внутренней стороны и выходит с тыльной. Пальцы при этом смотрят туда же, куда летит воображаемая частица. В таком случае большой палец покажет, куда она отклонится.
Интересно!
Важно отметить, что правило левой руки действует только для частиц со знаком «плюс». Чтобы узнать, куда отклонится отрицательный заряд, нужно четыре пальца направить в сторону, откуда летит частица. Все остальные манипуляции остаются прежними.
Следствия свойств силы Лоренца
Тело влетает в магнитном поле под каким-то определённым углом. Интуитивно понятно, что его величина имеет какое-то значение на характер воздействия на него поля, здесь нужно математическое выражение, чтобы стало понятнее. Следует знать, что как сила, так и скорость являются векторными величинами, то есть имеют направление. То же самое относится и к линиям магнитной напряженности. Тогда формулу можно записать следующим образом:
FЛ=qvBsinα,
sin α здесь – это угол между двумя векторными величинами: скоростью и потоком магнитного поля.
Как известно, синус нулевого угла также равен нулю. Получается, что если траектория движения частицы проходит вдоль силовых линий магнитного поля, то она никуда не отклоняется.
В однородном магнитном поле силовые линии имеют одинаковое и постоянное расстояние друг от друга. Теперь представим, что в таком поле перпендикулярно этим линиям движется частица. В этом случае сила Лоуренса заставит двигаться ее по окружности в плоскости, перпендикулярной силовым линиям. Чтобы найти радиус этой окружности, нужно знать массу частицы:
R=mvqB
Значение заряда не случайно взято как модуль. Это означает, что неважно, отрицательная или положительная частица входит в магнитное поле: радиус кривизны будет одинаков. Изменится только направление, в котором она полетит.
Во всех остальных случаях, когда заряд имеет определенный угол α с магнитным полем, он будет двигаться по траектории, напоминающей спираль с постоянным радиусом R и шагом h. Его можно найти по формуле:
R=mvsinαqB
h=2mvcosαqB
Еще одним следствием свойств этого явления является тот факт, что она не совершает никакой работы. То есть она не отдает и не забирает энергию у частицы, а лишь меняет направление ее движения.
Самая яркая иллюстрация этого эффекта взаимодействия магнитного поля и заряженных частиц – это северное сияние. Магнитное поле, окружающее нашу планету, отклоняет заряженные частицы, прилетающие от Солнца. Но так как оно слабее всего на магнитных полюсах Земли, то туда проникают электрически заряженные частицы, вызывая свечение атмосферы.
Центростремительное ускорение, которое придается частицам, используется в электрических машинах – электродвигателях. Хотя уместнее здесь говорить о силе Ампера – частном проявлении силы Лоуренса, которая воздействует на проводник.
Принцип действия ускорителей элементарных частиц также основан на этом свойстве электромагнитного поля. Сверхпроводящие электромагниты отклоняют частицы от прямолинейного движения, заставляя их двигаться по кругу.
Самое любопытное заключается в том, что сила Лоренца не подчиняется третьему закону Ньютона, который гласит, что всякому действию есть свое противодействие. Связано это с тем, что Исаак Ньютон верил, что всякое взаимодействие на любом расстоянии происходит мгновенно, однако это не так. На самом деле оно происходит с помощью полей. К счастью, конфуза удалось избежать, так как физикам удалось переработать третий закон в закон сохранения импульса, который выполняется в том числе и для эффекта Лоуренса.
Использование правила правой руки в электродинамике
Если в магнитном поле подвесить на тонком и гибком проводе рамку с током, то она будет поворачиваться и расположится определенным образом. Аналогично поведение магнитной стрелки. Это свидетельствует о векторном характере физической величины, характеризующей магнитное поле. При этом направление этого вектора будет связано с ориентацией рамки и стрелки. Физической векторной величиной, которая характеризует магнитное поле, стал вектор магнитной индукции ($\vec{B}$).
Ты эксперт в этой предметной области? Предлагаем стать автором Справочника Условия работы
Это один из главных параметров, описывающих состояние магнитного поля, поэтому необходимо уметь находить его величину и, конечно, направление.
Для определения направления вектора магнитной индукции используют:
- правило правого винта или
- правило правой руки.
Направлением вектора магнитной индукции, в месте локализации рамки с током, считают направление положительного перпендикуляра ($\vec{n}$) к этой рамке. Положительная нормаль ($\vec{n}$) будет иметь направление такое же, как направление поступательного перемещения правого винта, если его головку вращать по току в рамке (рис.1 (a)).
Рисунок 1. Определение направления вектора магнитной индукции. Автор24 — интернет-биржа студенческих работ
Так, обладая пробной рамкой с током, помещая ее в исследуемое поле, давая ей свободно вращаться в нем, можно определить, как направлен вектор магнитной индукции в каждой точке поля. Необходимо только дать рамке прийти в положение равновесия, затем использовать правило правого винта.
Готовые работы на аналогичную тему
Курсовая работа Правило левой и правой руки для магнитного поля 490 ₽ Реферат Правило левой и правой руки для магнитного поля 270 ₽ Контрольная работа Правило левой и правой руки для магнитного поля 200 ₽
Получить выполненную работу или консультацию специалиста по вашему учебному проекту Узнать стоимость
Теперь обратимся к правилу правой руки. Сожмем правую руку в неплотный кулак (рис.2). Отогнем большой палец на 90°. Руку разместим так, чтобы большой палец указывал направление течения тока, тогда согнутые остальные четыре пальца укажут направление линий магнитной индукции поля, которое создает ток. А мы помним, что касательная в каждой точке поля к силовой линии (линии магнитной индукции) указывает направление $\vec{B}$.
Рисунок 2. Правило правой руки. Автор24 — интернет-биржа студенческих работ
Рассмотрим соленоид. Обхватим правой ладонью его так, чтобы четыре пальца совпали с направлением тока в нем, тогда отогнутый на девяносто градусов палец укажет, как направлено магнитное поле, создаваемое у него внутри.
Нам известно, что если в магнитном поле перемещать проводник, то в этом проводнике будет возникать ток индукции. Правило правой руки можно использовать для определения направления течения тока индукции в таких проводниках. При этом:
- линии индукции магнитного поля должны входить в открытую ладонь правой руки,
- палец этой руки отогнуть на девяносто градусов, и направить по скорости перемещения проводника,
- вытянутые четыре пальца будут указывать, как направлен ток индукции.
Правилом правой руки можно воспользоваться при определении направления ЭДС индукции в контуре:
Согнутыми четырьмя пальцами правой руки охватить контур, в котором индуцируется ЭДС при изменении магнитного потока, отогнуть на девяносто градусов большой палец этой руки и направить его по направлению магнитного потока при его увеличении (или против направления магнитного потока при его уменьшении), тогда согнутые пальцы укажут на направление противоположное ЭДС.
Понятие напряженности электрического поля
Электромагнитное поле на самом деле состоит из двух половин – электрической и магнитной. Они точно близнецы, у которых все одинаково, но вот характер разный. А если приглядеться, то во внешности можно заметить небольшие различия.
То же самое касается и силовых полей. Электрическое поле тоже обладает напряженностью – векторной величиной, которая является силовой характеристикой. Она воздействует на частицы, которые в неподвижности находятся в нем. Само по себе оно не является силой Лоренца, ее просто нужно принимать во внимание, когда вычисляется воздействие на частицу в условиях наличия электрического и магнитного полей.
Магнитное поле
В соответствии с вышесказанным мы можем дать следующее определение магнитного поля.
Магнитным полем называется одна из двух сторон электромагнитного поля, возбуждаемая электрическими зарядами движущихся частиц и изменением электрического поля и характеризующаяся силовым воздействием на движущиеся зараженные частицы, а стало быть, и на электрические токи.
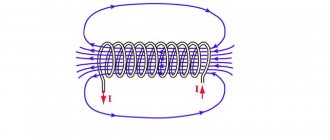
| Рисунок 1. Магнитное поле вокруг проводника с током |
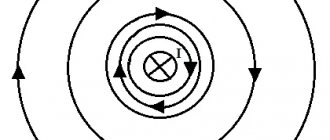
| Рисунок 2. Направление магнитных индукционных линий |
Если продеть через картон толстый проводник и пропустить по нему электрический ток, то стальные опилки, насыпанные на картон, расположатся вокруг проводника по концентрическим окружностям, представляющим собой в данном случае так называемые магнитные индукционные линии (рисунок 1). Мы можем передвигать картон вверх или вниз по проводнику, но расположение стальных опилок не изменится. Следовательно, магнитное поле возникает вокруг проводника по всей его длине.
Если на картон поставить маленькие магнитные стрелки, то, меняя направление тока в проводнике, можно увидеть, что магнитные стрелки будут поворачиваться (рисунок 2). Это показывает, что направление магнитных индукционных линий меняется с изменением направления тока в проводнике.
Магнитные индукционные линии вокруг проводника с током обладают следующими свойствами: 1) магнитные индукционные линии прямолинейного проводника имеют форму концентрических окружностей; 2) чем ближе к проводнику, тем гуще располагаются магнитные индукционные линии; 3) магнитная индукция (интенсивность поля) зависит от величины тока в проводнике; 4) направление магнитных индукционных линий зависит от направления тока в проводнике.
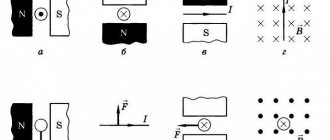
Чтобы показать направление тока в проводнике, изображенном в разрезе, принято условное обозначение, которым мы в дальнейшем будем пользоваться. Если мысленно поместить в проводнике стрелку по направлению тока (рисунок 3), то в проводнике, ток в котором направлен от нас, увидим хвост оперения стрелы (крестик); если же ток направлен к нам, увидим острие стрелы (точку).
Рисунок 3. Условное обозначение направления тока в проводниках
Примеры задачи
Задача 1
На заряд в 0,005 Кл, который движется в магнитном поле с индукцией 0,3 Тл, действует сила Лоренца. Вычислить ее, если скорость заряда 200 м/с, а движется он под углом 450 к линиям магнитной индукции.
| Дано: q = 0,005 Кл B = 0,3 Тл v = 200 м/с α = 450 | Решение: В условиях задачи нет упоминания электрического поля, поэтому силу Лоренца можно найти по следующей формуле: FЛ=qvBsinα=0,005×200×0,3×sin 450 =0,3×22=0,21 Н |
Задача 2
Определить скорость тела, имеющего заряд и которое движется в магнитном поле с индукцией 2 Тл под углом 900. Величина, с которой поле воздействует на тело, равна 32 Н, заряд тела – 5 × 10-3 Кл.
| Дано: q = 0,005 Кл B = 2 Тл FЛ = 32 Н α = 900 | Решение: Чтобы найти скорость заряда, необходимо несколько видоизменить формулу для нахождения силы Лоренца: FЛ=qvBsinαv=FЛqBsinα v=320,005×2×sin900=320,01×1=32000мс=32 км/с |