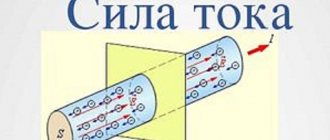
Сила лоренца | Формула и определение

Ученый физик из Франции Мари Ампер удивил мир многими потрясающими открытиями. В частности, он доказал взаимодействие проводника в магнитном поле с силой данного магнитного поля при наличии электрического тока. Из школьной программы мы знаем, что ток – это упорядоченное движение заряженных частиц (электронов), соответственно, электромагнитное поле также влияет на отдельно взятую заряженную частицу. Это действие известно в науке как сила Лоренца, для определения ее модуля в физике есть определенная формула.

История открытия

Впервые определить — что такое электромагнитная сила ученые пытались в 18 столетии. Тогда специалисты предположили следующее – к силе, сосредоточенной на магнитных полюсах, и на объектах с зарядом можно применить закон обратных квадратов. Тем не менее, практически доказать данное утверждение не получилось. Это сделал в конце 18 столетия Шарль Августин де Кулон, с помощью устройства для измерения незначительных сил, а именно торсионного баланса.

В первой половине 19 века были сделаны открытия, которые стали основой для дальнейшего развития теории электромагнитных полей. Доказано следующее – стрелка компаса находится под действием магнитной силы земли, кроме этого, выведена и доказана формула для вычисления угловой зависимости между различными элементами тока. Два данных открытия стали основой для теоретических разработок Майкла Фарадея, работы ученого дополнили расчетами и конкретными обоснованиями Лорд Кельвин, Джеймс Максвелл. Последний представил миру физики уравнение поля Максвелла, которое использовал Джей Томпсон, и вывел значение электромагнитной силы, действующей на каждую заряженную движущуюся частицу. Свои теоретические заключения он сформулировал формулой: F = q/2 v x B. Однако оказалось, что она не совсем корректна.

Только в конце 19 столетия ученому из Голландии Хендрику Лоуренсу удалось вывести правильную формулу, ее используют до сих пор, она названа именем ученого. Единица измерения силы Лоренца — Ньютон.

Формулировка и формулы

Частица с зарядом q испытывает силу F, когда движется со скоростью v в электрическом (E) и магнитном (B) полях. Определяется она как F = qE + qv x B и измеряется в единицах СИ — N (ньютон). С точки зрения декартовых компонентов имеется:

F x = q (E x + ⱴ y B z — ⱴ z B y);
F y = q (E y + ⱴ z B x — ⱴ x B z);
F z = q (E z + ⱴ x B y — ⱴ y B x).

E и B — функции положения времени. Следовательно, равенство может быть записано как F (r, ṙ, t, q) = q , где r — вектор положения заряженной частицы, t — время, а овердот — производная времени.

Ускорение частицы будет происходить в той же линейной ориентации, что и поле E, но станет изгибаться перпендикулярно как вектору мгновенной скорости v, так и полю B. Это говорит о соответствии формулы силы Лоренца и «правила левой руки». Также здесь будет работать и «правило буравчика» (если пальцы расширяются, чтобы указывать в направлении v, а затем скручиваются, показывая в сторону B, тогда большой палец будет смотреть на F).

Комбинация q E называется электрической силой, а q (v + B) — магнитной. В этом контексте её можно называть силой Лапласа. Она не влияет на мощность, потому что всегда перпендикулярна скорости частицы.

Для непрерывного распределения заряда в движении уравнение принимает вид dE = dq (E + v + B). Если обе части равенства будут разделены на объём небольшого фрагмента dV, результат будет выглядеть следующим образом: f = p (E + v x B). Поэтому непрерывным аналогом уравнения является f = pE + J x B, где J — плотность тока.

Суммарная сила — интеграл объёма по распределению заряда: F = ∫∫∫ (p E + J x B) dV. Устраняя p и J, используя уравнения Максвелла и манипулируя с помощью теорем векторного исчисления, эту форму можно использовать для получения тензора напряжения σ. В свою очередь, это можно объединить с вектором Пойнтинга s для получения электромагнитного тензора энергии-импульса T, используемого в общей теории относительности. Если разделить полный заряд и ток на их связанные частицы, то получится плотность силы Лоренца. Она, в свою очередь, может объяснить крутящий момент.

Что означает сила и ее формула

Силой Лоренца принято называть силу, влияющую на электрон, который движется и находится в магнитном поле. Речь идет о комбинации двух сил – магнитной, электрической, сконцентрированных на заряде. Сила Лоренца определяется следующими значениями:

индукцией;
величиной заряда;
скоростью передвижения частицы.

Направление заряженной частицы ортогонально плоскости, где находятся векторы скорости перемещения. Для силы Лоренца в физике существует равнодействующая сила – это сила Ампера.

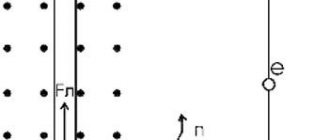
Для наглядной демонстрации искомой силы давайте вспомним опыт, который вам наверняка показывали на уроке физики — с магнитом, опилками металла, листом бумаги. Преподаватель подносил магнит к опилкам снизу, через бумагу и они выстраивались по четким линиям. Именно они образуют силовое поле магнита. Примечательно, что это замкнутое пространство без начала и конца. Речь идет о векторной величине, которая при любых обстоятельствах устремляется в сторону северного полюса магнита. Если в поле попадает заряженная частица, происходит смена траектории. Угол отклонения определяется скоростью движения частицы, а также силой, которая влияет на электрон. Это и есть искомая сила Лоренца, для ее вычисления применяют формулу: FЛ=qVB, здесь:

q – сила заряда (обозначается в Кулонах);
V – скорость передвижения заряда (обозначается в м/с);
В — индукция поля (обозначается в Тесла).

Определение силы, а также формула, предложенные в конце 19 столетия, актуальны и сегодня.

Направление силы

Указание силы Лоренца становится противоположным при соблюдении двух условий:

когда знак заряда также становится противоположным;
направления других векторов остаются неизменными.

Траекторию электрона принято называть винтовой линией.

Когда возникает

Параметры магнитного поля остаются неизменными, если заряженная частица неподвижна. Аналогично на проводник не действует сила Ампера, когда нет тока.

Чтобы определить модуль силы Лоренца потребуется соблюдение таких условий:

1. наличие заряду у частицы;

2. наличие магнитного поля;

3. частица должна двигаться.

Если не выполняется одно из трех условий, сила отсутствует.

Понятие напряженности электрического поля

Электромагнитное поле на самом деле состоит из двух половин – электрической и магнитной. Они точно близнецы, у которых все одинаково, но вот характер разный. А если приглядеться, то во внешности можно заметить небольшие различия.

То же самое касается и силовых полей. Электрическое поле тоже обладает напряженностью – векторной величиной, которая является силовой характеристикой. Она воздействует на частицы, которые в неподвижности находятся в нем. Само по себе оно не является силой Лоренца, ее просто нужно принимать во внимание, когда вычисляется воздействие на частицу в условиях наличия электрического и магнитного полей.

Электромагнитная индукция, магнитный поток

Под термином – магнитная индукция – понимают физическое свойство магнитного поля. Данная величина векторная, для ее обозначения используют символ В. Индукция характеризует силу, влияющую на заряженную частицу, которая перемещается в магнитном поле. Важно помнить, что сила, как и направление движения электрона перпендикулярны друг к другу.

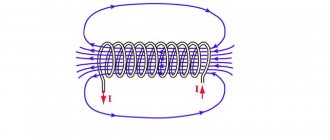
Индукция проявляется, когда магнит перемещается в катушке, а также появляется ток. Следовательно, магнитный поток пропорционально увеличивается.

Индукцию объясняют так – структура металла катушки кристаллическая, здесь находятся электрические заряды. При отсутствии влияния магнита на катушку эти заряды не двигаются. Когда она попадает в магнитное поле, появляется скорость заряда, поскольку электроны начинают двигаться. В проводнике формируется ток, его сила определяется параметрами магнита, проводника.

Полезно знать! Если проводник окружает магнитное поле, электроны сдвигаются од определенным углом, размещаются параллельно силовых линий.

Широкое применение

Первыми приборами для предполагаемых открытий стали циклотроны. Смысл их работы довольно прост: частицы двигаются полукругом. Каждый раз, когда они проходят определённую область, специальный модуль включает электрическое поле, чтобы ускорить их.

Масс-спектрометры применяются для идентификации атомов и молекул. Они используются в следующих устройствах:

электродвигатели;
громкоговорители;
рельсовые пистолеты.

Способность силы Лоренца связывать механическое смещение с электрическим током представляет большой интерес для медицинской акустики. Например, разрабатывался гидрофон для картирования скорости частиц акустического поля. Предполагалось, что он будет построен с использованием тонкого медного провода и внешнего магнитного поля.

Модель была разработана для определения взаимосвязи между акустическим давлением и измеренным электрическим током, который индуцируется, когда провод вибрирует в акустическом поле ультразвукового преобразователя.

Созданный прототип был охарактеризован. Было исследовано его пространственное разрешение, частотная характеристика, чувствительность, надёжность и характеристика направленности. Был также изучен метод визуализации, называемый электрической импедансной томографией. В этом методе биологическая ткань вибрирует ультразвуком в магнитном поле, которое индуцирует электрический ток. Этот метод был применён для визуализации желатинового фантома, образца мышц говядины и термического поражения в образце куриной грудки. Это показало, что метод может быть полезен для обеспечения дополнительного контраста по сравнению с обычной ультразвуковой визуализацией.

Закон электромагнитной индукции

Простыми словами один из основных законов физики сформулируется так – изменения магнитного поля, при условии, что оно пересекает контур, сопровождаются появлением электродвижущей силы. Она пропорциональна скорости изменения магнитного поля. Не имеет значения – что спровоцировало такие изменения магнитного поля.

Закон в начале 19 столетия предложил Майкл Фарадей. Именно на законе Фарадея основана работа трансформаторов, генераторов, дросселей. Контуром является катушка с проводом, магнитное поле формирует магнит. Для проведения замеров электродвижущей силы провод подключают к вольтметру.

Рассмотрим два варианта:

магнит неподвижно расположен над катушкой – формируется постоянное поле, параметры которого не меняются, соответственно, электродвижущая сила не возникает;
положение магнита меняется – любые движения магнита вызывают изменения поля, это источник появления электродвижущей силы и напряжения, замеры ЭДС можно проводить, пока магнит передвигается.

ЭДС в контуре формирует ток, его ориентацию определяют посредством правила Ленца, сформулированное так – ток, появляющийся при изменениях в магнитном поле, проходящим через любой контур, сдерживает данные изменения. Таким образом, когда на катушку действует магнит, происходит следующее – увеличивается магнитный поток, появляется ток и магнитное поле, препятствующее увеличению поля магнита.

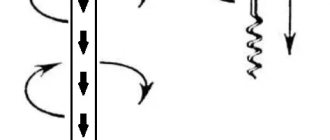
Полезно знать! Чтобы понять, куда движется ток, необходимо вкрутить буравчик в направлении северного полюса, в аналогичном направлении формируется магнитное поле. Это означает, что ток движется параллельно часовой стрелке.

Если на катушку не действует магнит, происходит следующее – магнитный поток уменьшается, соответственно, магнитное поле тока сдерживает уменьшение поля магнита. Чтобы определить, в какую сторону движется ток, буравчик выкручивается, его движение указывает – куда направлен ток, а именно – в противоположном от часовой стрелки направлении.

Теория хаоса

Можно ли прогнозировать хаотическое движение элементов какой-либо системы? От чего зависит хаотическая динамика? Может ли, наконец, взмах крыла бабочки вызвать торнадо? Некоторые важные ответы на эти и другие вопросы нашел американский метеоролог Эдвард Лоренц, (невольный) автор термина «эффект бабочки» и создатель «странного аттрактора». Рассказываем об этом в первом материале, посвященном самым интересным дифференциальным уравнениям.

В 1972 году профессор метеорологии из Массачусетского технологического института Эдвард Лоренц собирался выступить на конференции, но в пылу работы не успел отправить тему своей лекции. Организатор, спешивший разослать приглашения, выбрал заголовок за него: «Предсказуемость: может ли взмах крыла бабочки в Бразилии вызвать торнадо в Техасе?» Так и появился термин «эффект бабочки», известный сегодня всему миру.

Эдвард Лоренц родился в 1917 году в небольшом городке в штате Коннектикут. Изучать атмосферные явления он решил еще в детстве, испытав потрясение от того, с какой легкостью солнечная погода может смениться бурей с громом и молниями.

Путь к исполнению мечты вышел долгим: магистратура в Гарварде, работа метеорологом в авиационном подразделении Армии США, защита диссертации в послевоенный период, наконец, должность научного сотрудника и, позже, профессора в MIT.

В своем выступлении Лоренц выделил несколько ключевых идей:

⦁ Если взмах крыла бабочки может вызвать торнадо, то точно так же на это способны все предыдущие и будущие взмахи, равно как и взмахи остальных миллионов бабочек, не говоря уже об активности бесчисленного населения нашей планеты.

⦁ Если взмах крыла бабочки способен вызывать торнадо, то в равной степени этот же взмах может его предотвратить.

Взмах крыла бабочки в данном контексте должен восприниматься как маленькое изменение начальных условий исследуемой системы, способное как вызвать торнадо, так и изменить его траекторию или вообще стать причиной его затухания.

В отличие от эффекта домино, где конкретное (обычно незначительное) действие приводит к конкретному (обычно значительному) результату, причем происходит это однозначно, взмах бабочки может не иметь никакого влияния на поведение торнадо.

Система Лоренца

Лоренц изучал конвекцию (теплообмен, возникающий за счет движения молекул жидкости или газа) в атмосфере Земли. Для описания подобных физических процессов часто пользуются моделью, которая включает в себя уравнения Навье-Стокса, описывающие движение вязкой ньютоновской жидкости (за исключением некоторых частных случаев, их решения в общем виде на данный момент неизвестны):

⦁ Уравнение движения в векторном виде:

⦁ Уравнение теплопроводности, описывающее распределение температуры в пространстве с течением времени:

⦁ Уравнение непрерывности, которое, по своей сути, описывает принцип сохранения массы чего-либо:

В оригинале эти три составляющие дают следующую систему:

Мы не будем углубляться в детальное объяснение всего вышеизложенного. Достаточно лишь понимать, что это довольно сложная модель, и Лоренцу в результате многостраничных выкладок удалось построить ее упрощение:

Здесь переменная с точкой сверху означает ее производную по времени. Более подробно:

x отвечает за интенсивность конвекции;
y отображает разность между температурами входящих и нисходящих потоков;
z характеризует отклонение вертикального температурного профиля от линейной зависимости;
σ > 1 — число Прандтля (критерий подобия тепловых процессов в жидкостях и газах);
ρ > 0 — число Рэлея (отображает поведение жидкости под воздействием градиента температуры);
β > 0 — число, отражающее геометрию конвективной ячейки.

С помощью этой системы уравнений можно рассчитать, как будет вести себя текучая среда, которую равномерно разогревают снизу и охлаждают сверху. Так, как это происходит с воздушными потоками в атмосфере. В частности, она позволяет понять, к какому результату приведет даже небольшое изменение исходных параметров.

Хаотическое движение

Перед тем как приступить к непосредственному анализу полученной системы, рассмотрим некоторые комбинации траекторий. Для наглядности, воспользуемся теми же значениями параметров, что и сам Лоренц: σ = 10, ρ = 28, β = 8/3.

Изобразим движение двух точек, расстояние между которыми изначально невелико:

⦁ P0 = (0, 1, 1) ⦁ P1 = (0, 1, 1,01)

Довольно интересный результат! Поначалу траектории почти неразличимы, потом они отклоняются совсем ненамного, после чего разница становится уже значительной.

Попробуем еще раз, однако теперь возьмем точки на значительном отдалении друг от друга:

⦁ P0 = (−25, 20, −15) ⦁ P1 = (−15, 40, 15)

Даже несмотря на подобную разницу начальных условий, траектории попадают на фигуру, которую впоследствии не покидают. Очень странно, их будто что-то притягивает…

Странный аттрактор Лоренца

Действительно, эта фигура так и называется — странный аттрактор Лоренца (от английского attract

— «притягивать»).

Формальное математическое определение звучит так: аттрактор — такое подмножество фазового пространства, что все траектории, стартующие не слишком далеко от него, стремятся к нему с течением времени. (Это одно из возможных определений понятия аттрактора, существуют и другие, не эквивалентные данному.)

Слово же «странный» здесь выступает в таком ключе: аттрактор как множество не представим в виде кривой или поверхности, он имеет более сложную, фрактальную структуру. Траектории аттрактора не замыкаются, а малые отклонения постоянно накапливаются, причем экспоненциально.

Сказанное выше можно проиллюстрировать так: две траектории, выпущенные из близких точек, со временем разбегаются достаточно далеко. Причем, чтобы отдалить момент разбегания, например, на одну секунду, нужно уменьшить расстояние между начальными точками, скажем, вдвое. А чтобы на две секунды — вчетверо. А на три — в восемь раз, и так далее.

Это означает, что, даже используя мощный компьютер, мы не можем просчитать траекторию, проходящую вблизи аттрактора, с разумной точностью на протяжении длительного промежутка времени. На каждом шаге вычислений неизбежно вносятся ошибки (из-за округления чисел и погрешностей численных методов), которые быстро накапливаются и приводят к тому, что найденная траектория сильно отличается от настоящей.

Такое искажение невозможно исправить, просто увеличивая мощность компьютера. Подобное явление называется «динамическим хаосом».

Ниже представлена модель странного аттрактора, с которой можно поэкспериментировать, меняя входящие значения. Для желающих более подробно изучить математическую сторону припасен еще один раздел сразу после модели.

Вы можете покрутить модель или увеличить/уменьшить ее масштаб (с помощью кнопок мыши на десктопе или пальцами на экране смартфона). Значение бегунков сверху вниз:

значение параметра σ;
значение параметра ρ;
значение параметра β;
плотность траекторий.

Оранжевые сферы — точки, движущиеся согласно системе Лоренца. Соответственно, синие линии — траектории этих точек.

Немного математики

Система Лоренца обладает несколькими замечательными свойствами:

⦁ Правая часть системы не имеет свободных членов, то есть она однородна.

⦁ Если тройка (x, y, z) является решением, то и (-x, -y, z) также подходит — система обладает симметрией.

⦁ Все траектории системы ограничены некоторым предельным множеством в силу отрицательности дивергенции векторного поля:

Иными словами, поток сжимает объем фазового пространства — это называется диссипативной системой.

Система Лоренца обладает точками равновесия, причем одна из них очевидна — E0 = (0, 0, 0). Попробуем найти другие:

В предположении, что x ≠ 0 (иначе решением будет (0, 0, 0)) и ρ ≥ 1, получим:

Таким образом, мы получили еще две точки равновесия при x ≠ 0, ρ ≥ 1:

Исследуем эти точки на устойчивость при помощи якобиана:

Начнем с точки E0 = (0, 0, 0):

Подкоренное выражение больше нуля, поэтому все собственные значения являются вещественными.

при ρ <� 1 корни отрицательные — устойчивый узел;
при ρ = 1 существует нулевой корень — точка бифуркации;
при ρ > 1 существует положительный корень — неустойчивое седло.

Для оставшихся двух точек мы не будем подробно углубляться в выкладки, чтобы сохранить простоту восприятия.

Оказывается, что они либо одновременно устойчивы, либо одновременно неустойчивы. Асимптотическая устойчивость имеет место при справедливости одного из следующих условий:

Хаос по определению

Детерминизм зачастую приравнивался к предсказуемости, но Лоренцу удалось показать, что детерминизм способен дать лишь краткосрочное предсказание поведения системы, тогда как в долгосрочной перспективе последствия могут быть непредсказуемы. Именно это и означает термин «хаос».

Однако не стоит путать хаос с хаотичностью — аттрактор Лоренца яркий тому пример, ведь все траектории так или иначе ограничены и не покидают определенное множество.

А что же погода? Работа Лоренца привела к усовершенствованию систем, используемых для составления ее прогнозов:

на метеостанциях стали собирать значительно больше данных;
для вычислений в симуляциях моделей начали использоваться методы, позволяющие добиться большей точности;
метеорологи, проводящие эксперименты, осознали важность чувствительности системы к начальным условиям — они запускают большое количество симуляций, входные данные для которых обладают едва заметной разницей, и таким образом явление, происходящее в большинстве случаев, «признается» наиболее вероятным.

Слова практика: что мешает предсказывать погоду на месяц вперед?

Теоретически прогнозировать погоду по дням в деталях можно на две недели, а практически, на современном уровне развития науки, — на 5-7 дней. Я могу, конечно, повторить любимые мантры метеорологов: атмосфера — это хаотическая система с хорошо выраженной диссипацией и тому подобное. На самом деле прогноз погоды… — это решение системы дифференциальных уравнений. Точность результата, то есть точность решения этих уравнений, зависит от начальных данных. Так вот, согласно современному пониманию фундаментальных законов природы, теоретическая минимальная ошибка начальных данных ведет к тому, что через две недели решение задачи перестает зависеть от этих самых начальных данных.
Другими словами, как бы мы ни старалась, спрогнозировать ситуацию более чем на две недели вперед уже невозможно. Увы! И это такая непростая философская ситуация, которую впервые осознали именно метеорологи: сколько ни развивай науку, две недели — это порог, и за этим порогом невозможно по дням прогнозировать.

Из интервью Романа Вильфанда, научного руководителя Гидрометцентра России

Несмотря на кажущуюся простоту одноименной системы, Лоренцу удалось изменить взгляды многих математиков и физиков на привычные им вещи и стать основоположником новой ветви теории хаоса.

Лев Хорошанский

Литература

Lorenz, E.
Predictability: Does the Flap of a Butterfly’s Wings in Brazil Set off a Tornado in Texas? 1972.
Ghys, E.
The Lorenz Attractor, a Paradigm for Chaos. 2010.

Knill, O.

The Lorenz System. 2005.

Semenova, E.

Chaotic behavior of dynamical systems. 2014.

Энергия магнитного поля тока

Параметр указывает, какой объем работы совершает ток в проводнике, чтобы сформировать магнитное поле. Значение напрямую определяется индуктивностью проводника, вокруг которого формируется поле.

Для вычисления энергии существует формула, равная произведению индуктивности цепи, силы тока, возведенной в квадрат, полученный результат делится на два: W = LI2/2.

Передвижение частицы в магнитном поле

Для наглядности рассмотрим несколько вариантов. Направление частицы перпендикулярно полю, она движется по окружности, радиус которого неизменный.

Сила Лоренца направлена по радиусу к центральной точке окружности, появляется радиальное ускорение. Если применить второй закон Ньютона, получим следующее уравнение: Fl = maT = mv2/R. Из этого уравнения получаем следующее: mv2/R = qvB. Используя это выражение, можно вывести формулу для вычисления угловой скорости электрона: w = v/R = qB/m.

Если в данном выражении значения q, m, B – величины неизменные, угловая скорость также остается неизменной. На радиус передвижения влияет только скорость.

Сила Лоренца формирует ускорение и устремлена внутрь окружности. Направление положительно заряженной частицы, а также винта совпадают, но ориентация винта и магнитного поля противоположны. Соответственно, отрицательно заряженная частица вращается в противоположную сторону.

Сила Лоренца нулевая при условии, что движение частицы, вектор индукции параллельны. Электрон движется равномерно, прямолинейно.

Третий вариант – электрон передвигается в поле, вектор скорости образует угол с магнитным полем. Скорость раскладывают на такие составляющие:

направлена вдоль поля – v = vcos0;
направлена перпендикулярно полю – v = vsin0.

Для определения движения частицы нужно вычислить сумму двух движений – параллельно магнитному поля (vcos0), вращение по окружности (w = qB/m). Резюмируем – частица движется по спирали.

Действие магнитного поля на движущийся заряд

— сила, действующая со стороны магнитного поля на движущуюся электрически заряженную частицу.
где q — заряд частицы;

V — скорость заряда;

B — индукции магнитного поля;

a — угол между вектором скорости заряда и вектором магнитной индукции.

Направление силы Лоренца определяется по правилу левой руки:

Если поставить левую руку так, чтобы перпендикулярная скорости составляющая вектора индукции входила в ладонь, а четыре пальца были бы расположены по направлению скорости движения положительного заряда (или против направления скорости отрицательного заряда), то отогнутый большой палец укажет направление силы Лоренца:

Так как сила Лоренца всегда перпендикулярна скорости заряда, то она не совершает работы (т.е. не изменяет величину скорости заряда и его кинетическую энергию).

Если заряженная частица движется параллельно силовым линиям магнитного поля, то Fл = 0 , и заряд в магнитном поле движетсяравномерно и прямолинейно.

Если заряженная частица движется перпендикулярно силовым линиям магнитного поля, то сила Лоренца является центростремительной:

и создает центростремительное ускорение равное:

В этом случае частица движется по окружности.

Согласно второму закону Ньютона: сила Лоренца равнв произведению массы частицы на центростремительное ускорение:

тогда радиус окружности:

а период обращения заряда в магнитном поле:

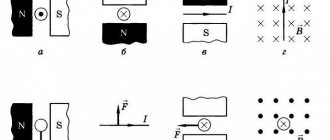
Так как электрический ток представляет собой упорядоченное движение зарядов, то действие магнитного поля на проводник с током есть результат его действия на отдельные движущиеся заряды. Если внести проводник с током в магнитное поле (фиг.96,а), то мы увидим, что в результате сложения магнитных полей магнита и проводника произойдет усиление результирующего магнитного поля с одной стороны проводника (на чертеже сверху) и ослабление магнитного поля с другой стороны проводника (на чертеже снизу). В результате действия двух магнитных полей произойдет искривление магнитных линий и они, стремясь сократиться, будут выталкивать проводник вниз (фиг. 96, б).

Направление силы, действующей на проводник с током в магнитном поле, можно определить по «правилу левой руки». Если левую руку расположить в магнитном поле так, чтобы магнитные линии, выходящие из северного полюса, как бы входили в ладонь, а четыре вытянутых пальца совпадали с направлением тока в проводнике, то большой отогнутый палец руки покажет направление действия силы. Сила Ампера , действующая на элемент длины проводника, зависит: от величины магнитной индукции В, величины тока в проводнике I, от элемента длины проводника и от синуса угла а между направлением элемента длины проводника и направлением магнитного поля.

Эта зависимость может быть выражена формулой:

Для прямолинейного проводника конечной длины, помещенного перпендикулярно к направлению равномерного магнитного поля, сила, действующая на проводник, будет равна:

Из последней формулы определим размерность магнитной индукции.

Так как размерность силы:

т. е. размерность индукции такая же, какая была получена нами из закона Био и Савара.

Тесла (единица магнитной индукции)

Тесла, единица магнитной индукции Международной системы единиц, равная магнитной индукции, при которой магнитный поток сквозь поперечное сечение площадью 1 м2 равен 1 веберу. Названа по имени Тесла. Обозначения: русское тл, международное Т. 1 тл = 104 гс(гаусс).

Магни?тный моме?нт, магни?тный дипо?льный моме?нт — основная величина, характеризующая магнитные свойства вещества. Магнитный момент измеряется в А⋅м2 или Дж/Тл (СИ), либо эрг/Гс (СГС), 1 эрг/Гс = 10-3 Дж/Тл. Специфической единицей элементарного магнитного момента является магнетон Бора. В случае плоского контура с электрическим током магнитный момент вычисляется как

где — сила тока в контуре, — площадь контура, — единичный вектор нормали к плоскости контура. Направление магнитного момента обычно находится по правилу буравчика: если вращать ручку буравчика в направлении тока, то направление магнитного момента будет совпадать с направлением поступательного движения буравчика.

Для произвольного замкнутого контура магнитный момент находится из:

где — радиус-вектор, проведенный из начала координат до элемента длины контура

В общем случае произвольного распределения токов в среде:

где — плотность тока в элементе объёма .

Итак, на контур с током в магнитном поле действует вращающий момент. Контур ориентируется в данной точке поля только одним способом. Примем положительное направление нормали за направление магнитного поля в данной точке. Вращающий момент прямо пропорционален величине тока I, площади контура S и синусу угла между направлением магнитного поля и нормали .

здесь М – вращающий момент, или момент силы, – магнитный момент контура (аналогично – электрический момент диполя).

В неоднородном поле ( ) формула справедлива, если размер контура достаточно мал (тогда в пределах контура поле можно считать приближенно однородным). Следовательно, контур с током по-прежнему стремится развернуться так, чтобы его магнитный момент был направлен вдоль линий вектора .

Но, кроме того, на контур действует результирующая сила (в случае однородного поля и . Эта сила действует на контур с током или на постоянный магнит с моментом и втягивает их в область более сильного магнитного поля. Работа по перемещению контура с током в магнитном поле.

Нетрудно доказать, что работа по перемещению контура с током в магнитном поле равна , где и — магнитные потоки через площадь контура в конечном и начальном положениях. Эта формула справедлива, если ток в контуре постоянен, т.е. при перемещении контура не учитывается явление электромагнитной индукции.

Формула справедлива и для больших контуров в сильно неоднородном магнитном поле (при условии I=const).

Наконец, если контур с током не смещать, а изменять магнитное поле, т.е. изменять магнитный поток через поверхность, охватываемую контуром, от значения до то для этого надо совершить ту же работу . Эта работа называется работой изменения магнитного потока, связанного с контуром. Потоком вектора магнитной индукции (магнитным потоком) через площадку dS называется скалярная физическая величина, которая равна

(1)

где Bn=Вcosα — проекция вектора В на направление нормали к площадке dS (α — угол между векторами n и В), dS = dSn — вектор, у которого модуль равен dS, а направление его совпадает с направлением нормали n к площадке. Поток вектора В может быть как положительным, так и отрицательным в зависимости от знака cosα (задается выбором положительного направления нормали n). Поток вектора В обычно связывают с контуром, по которому течет ток. В этом случае положительное направление нормали к контуру нами задавалось: оно связывается с током правилом правого винта. Значит, магнитный поток, который создается контуром, через поверхность, ограниченную им самим, всегда положителен.

Поток вектора магнитной индукции ФB через произвольную заданную поверхность S равен

(2)

Для однородного поля и плоской поверхности, которая расположена перпендикулярно вектору В, Bn=B=const и

Из этой формулы задается единица магнитного потока вебер (Вб): 1 Вб — магнитный поток, который проходит сквозь плоскую поверхность площадью 1 м2, который расположен перпендикулярно однородному магнитному полю и индукция которого равна 1 Тл (1 Вб=1 Тл•м2).

Теорема Гаусса для поля В: поток вектора магнитной индукции сквозь любую замкнутую поверхность равен нулю:

(3)

Эта теорема является отражением факта, что магнитные заряды отсутствуют, вследствие чего линии магнитной индукции не имеют ни начала, ни конца и являются замкнутыми.

Следовательно, для потоков векторов В и Е сквозь замкнутую поверхность в вихревом и потенциальном полях получаются различные формулы.

В качестве примера найдем поток вектора В сквозь соленоид. Магнитная индукция однородного поля внутри соленоида с сердечником с магнитной проницаемостью μ, равна

Магнитный поток сквозь один виток соленоида площадью S равен

а полный магнитный поток, который сцеплен со всеми витками соленоида и называемый потокосцеплением,

Правило левой руки для силы Лоренца

Хотите знать, куда направлена сила Лоренца? Используйте правило левой руки. Суть данного правила такова – раскрытую левую ладонь ставят перпендикулярно, одновременно с этим параллельно линиям поля. Тогда четыре указывают движение тока, большой палец, отогнутый на 90 градусов, демонстрирует силу Лоренца.

Существует еще один метод определить ориентацию вектора силы Лоренца по правилу левой руки в физике. Большой, указательный, средний пальцы располагают под углом 90 градусов. Мы получим следующее:

средний демонстрирует движение тока;
указательный – магнитное поле;
большой – силу Лоренца.

Рассмотрим правило на конкретном примере. Например, электрон движется на человека. Соответственно, справа северный полюс, слева южный полюс. Данная формулировка верна для протона. Поскольку электрон заряжен отрицательно, четыре пальца правой руки вытягиваются навстречу движению протона – вперед. Магнитное поле формируется в сторону южного полюса. Поставьте левую ладонь ребром, тогда линии поля проходят сквозь ладонь, четыре пальца смотрят вперед, а большой палец, отогнутый на 90 градусов, демонстрирует векторное указание силы Лоренца – снизу вверх.

Правило правой руки

Прежде чем разобраться в правиле правой руки, необходимо уяснить, что любая сила и сила Лоренца не исключение – вектор, а это означает, что у данного параметра есть два значения – величина и указание. Если знать ориентацию множителей, определить направление векторного произведения не составит труда. Для этого потребуется правило левой или правой руки. Данное правило известно под название правила Буравчика или винта. Оно применимо не только к определению указания вектора силы Лоренца, но и к определению ориентации любых других векторных произведений.

Для лучшего понимания правил:

ионы с отрицательным зарядом, а также электроны всегда направлены от катода к аноду;
ионы с положительным зарядом, а также протоны направлены от анода к катоду;
электрический ток движется в направлении, которое противоположно направлению электронов.

Для определения ориентации искомой силы Лоренца потребуется поставить правую ладонь таким образом, чтобы ладонь и направление тока были направлены параллельно. В этом случае вращение буравчика или в данном конкретном примере большого пальца укажет сторону вектора индукции.

Если объяснить простыми словами, правой рукой необходимо вкручивать штопор.

Важно! Направление, а также угол, в котором заряженная частица отклонится от траектории под влиянием магнитного поля, определяется зарядом частицы.

Применение силы Лоренца в технике

Наиболее масштабно сила Лоренц представлена в магнитном поле Земли. Наша планета представляет собой магнит. Соответственно, заряженные частицы, расположенные у северного и южного магнитных полюсов движутся по спирали, сталкиваются с атомами, которые находятся в верхних слоях атмосферы. Сейчас мы описали механизм появления северного сияния. Однако есть и другие, частные случаи применения силы Лоренца.

Электрический генератор

Когда ученые доказали, что на проводник с током действует магнитное поле, данное открытие решили применить для того, чтобы заставить двигаться проводник, расположенный в магнитном поле. Таким образом, магнетизм удалось трансформировать в механическое движение, соответственно, создать двигатель.

Упрощенная модель механизма состоит из статора (неподвижная часть и закрепленные магниты), внутри которого вращается ротор (рамка, выполненная из материала-проводника). Для подведения тока к рамке ее подсоединяют к клеммам посредством контактов. Теперь модель двигателя подключают к источнику электроэнергии, в результате рамка вращается.

Важно! В двигателях, а также генераторах именно сила Лоренца заставляет ротор двигаться под влиянием электромагнитного поля, статора.

Спектрограф

Принцип функционирования прибора такой – источник заряженных частиц помещается в вакуумную камеру, так исключается вероятность действия воздуха на заряженные частицы. Внутри прибора искусственно формируется электрическое поле, под действием которого частицы с зарядом ускоряются, проходят по дуге и ударяются о фотопластину, на ней остаются характерные следы. Радиус траектории меняется в зависимости от удельного заряда. Радиус можно измерять, а затем вычислить массу заряженной частицы.

Интересный факт! Спектрографы используются для изучения состава грунта с Луны.

Кинескоп

До недавнего времени кинескопом был оснащен каждый телевизор, а при отсутствии силы Лоренца, техника не работала бы. Рассмотрим принцип действия кинескопа – это вакуумный баллон, внутри которого расположен источник электронов. Катушки формируют магнитное поле, именно оно управляет электронным лучом. Экран покрыт особым веществом, которое светится, когда на него действуют электроны. Траекторией электронов управляет магнитное поле, а скоростью управляет электрическое поле. Таким образом, если направлять заряженные частицы в конкретные точки экрана, он будет светиться в соответствии с изображением.

Полезно знать! Поднесите магнит к экрану, и вы увидите, как исказится изображение, так как изменится траектория заряженных частиц, ведь на них начнет действовать магнитное поле магнита.

Циклоторон

В данном приборе используется зависимость частоты вращения частицы с зарядом от скорости передвижения в магнитном поле. Основная сфера применения циклотрона – разгон частиц до максимальных скоростей.

Прибор представляет собой два полуцилиндра полые внутри, визуально напоминающие букву D. Их устанавливают прямыми гранями друг к другу и помещают в магнитное поле. Между гранями появляется электрическое поле, его частота аналогична частоте вращения заряженных частиц. В один период вращения каждая частица дважды попадает под влияние электрического поля, при этом скорость движения увеличивается и в определенный момент, когда скорость достигает максимума, частица вылетает через отверстие.