магнитный потокпрезентация к уроку по физике (9 класс) по теме

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: явление электромагнитной индукции, магнитный поток, закон электромагнитной индукции Фарадея, правило Ленца.

Опыт Эрстеда показал, что электрический ток создаёт в окружающем пространстве магнитное поле. Майкл Фарадей пришёл к мысли, что может существовать и обратный эффект: магнитное поле, в свою очередь, порождает электрический ток.

Иными словами, пусть в магнитном поле находится замкнутый проводник; не будет ли в этом проводнике возникать электрический ток под действием магнитного поля?

Через десять лет поисков и экспериментов Фарадею наконец удалось этот эффект обнаружить. В 1831 году он поставил следующие опыты.

1. На одну и ту же деревянную основу были намотаны две катушки; витки второй катушки были проложены между витками первой и изолированы. Выводы первой катушки подключались к источнику тока, выводы второй катушки — к гальванометру (гальванометр — чувствительный прибор для измерения малых токов). Таким образом, получались два контура: «источник тока — первая катушка» и «вторая катушка — гальванометр».

Электрического контакта между контурами не было, только лишь магнитное поле первой катушки пронизывало вторую катушку.

При замыкании цепи первой катушки гальванометр регистрировал короткий и слабый импульс тока во второй катушке.

Когда по первой катушке протекал постоянный ток, никакого тока во второй катушке не возникало.

При размыкании цепи первой катушки снова возникал короткий и слабый импульс тока во второй катушке, но на сей раз в обратном направлении по сравнению с током при замыкании цепи.

Вывод

.

Меняющееся во времени магнитное поле первой катушки порождает (или, как говорят, индуцирует

) электрический ток во второй катушке. Этот ток называется
индукционным током
.

Если магнитное поле первой катушки увеличивается (в момент нарастания тока при замыкании цепи), то индукционный ток во второй катушке течёт в одном направлении.

Если магнитное поле первой катушки уменьшается (в момент убывания тока при размыкании цепи), то индукционный ток во второй катушке течёт в другом направлении.

Если магнитное поле первой катушки не меняется (постоянный ток через неё), то индукционного тока во второй катушке нет.

Обнаруженное явление Фарадей назвал электромагнитной индукцией

(т. е. «наведение электричества магнетизмом»).

2. Для подтверждения догадки о том, что индукционный ток порождается переменным

магнитным полем, Фарадей перемещал катушки друг относительно друга. Цепь первой катушки всё время оставалась замкнутой, по ней протекал постоянный ток, но за счёт перемещения (сближения или удаления) вторая катушка оказывалась в переменном магнитном поле первой катушки.

Гальванометр снова фиксировал ток во второй катушке. Индукционный ток имел одно направление при сближении катушек, и другое — при их удалении. При этом сила индукционного тока была тем больше, чем быстрее перемещались катушки

.

3. Первая катушка была заменена постоянным магнитом. При внесении магнита внутрь второй катушки возникал индукционный ток. При выдвигании магнита снова появлялся ток, но в другом направлении. И опять-таки сила индукционного тока была тем больше, чем быстрее двигался магнит.

Эти и последующие опыты показали, что индукционный ток в проводящем контуре возникает во всех тех случаях, когда меняется «количество линий» магнитного поля, пронизывающих контур. Сила индукционного тока оказывается тем больше, чем быстрее меняется это количество линий. Направление тока будет одним при увеличении количества линий сквозь контур, и другим — при их уменьшении.

Замечательно, что для величины силы тока в данном контуре важна лишь скорость изменения количества линий. Что конкретно при этом происходит, роли не играет — меняется ли само поле, пронизывающее неподвижный контур, или же контур перемещается из области с одной густотой линий в область с другой густотой.

Такова суть закона электромагнитной индукции. Но, чтобы написать формулу и производить расчёты, нужно чётко формализовать расплывчатое понятие «количество линий поля сквозь контур».

Магнитный поток

Понятие магнитного потока как раз и является характеристикой количества линий магнитного поля, пронизывающих контур.

Для простоты мы ограничиваемся случаем однородного магнитного поля. Рассмотрим контур площади , находящийся в магнитном поле с индукцией .

Пусть сначала магнитное поле перпендикулярно плоскости контура (рис. 1).

Рис. 1.

В этом случае магнитный поток определяется очень просто — как произведение индукции магнитного поля на площадь контура:

(1)

Теперь рассмотрим общий случай, когда вектор образует угол с нормалью к плоскости контура (рис. 2).

Рис. 2.

Мы видим, что теперь сквозь контур «протекает» лишь перпендикулярная составляющая вектора магнитной индукции (а та составляющая, которая параллельна контуру, не «течёт» сквозь него). Поэтому, согласно формуле (1), имеем . Но , поэтому

(2)

Это и есть общее определение магнитного потока в случае однородного магнитного поля. Обратите внимание, что если вектор параллелен плоскости контура (то есть ), то магнитный поток становится равным нулю.

А как определить магнитный поток, если поле не является однородным? Укажем лишь идею. Поверхность контура разбивается на очень большое число очень маленьких площадок, в пределах которых поле можно считать однородным. Для каждой площадки вычисляем свой маленький магнитный поток по формуле (2), а затем все эти магнитные потоки суммируем.

Единицей измерения магнитного потока является вебер

(Вб). Как видим,

Вб = Тл · м = В · с. (3)

Почему же магнитный поток характеризует «количество линий» магнитного поля, пронизывающих контур? Очень просто. «Количество линий» определяется их густотой (а значит, величиной — ведь чем больше индукция, тем гуще линии) и «эффективной» площадью, пронизываемой полем (а это есть не что иное, как ). Но множители и как раз и образуют магнитный поток!

Теперь мы можем дать более чёткое определение явления электромагнитной индукции, открытого Фарадеем.

Электромагнитная индукция

— это явление возникновения электрического тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего контур
.

Энергия электрического поля

При зарядке конденсатора энергия запасается в виде энергии электрического поля и может быть возвращена источнику при преобразовании в другой вид энергии.

Выражение энергии через характеристики конденсатора

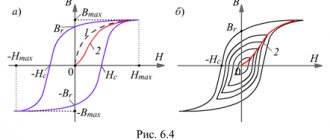
Заряд конденсатора образуется переносом заряженных частиц с одной обкладки на другую под действием внешнего источника энергии. Работа, совершенная при переносе единицы заряда, численно равна напряжению между обкладками. Если бы напряжение в процессе зарядки не изменялось, то энергию можно было бы определить произведением напряжения и заряда [см. формулу (1.5)]. Однако в процессе накопления заряда растет и напряжение, поэтому при определении энергии, затраченной на образование заряда, нужно учесть зависимость между напряжением и зарядом (7.28). Если емкость конденсатора — величина постоянная, зависимость между напряжением и зарядом графически выражается прямой линией (рис. 11.1).

Рис. 11.1. К определению энергии электрического поля

Предположим, что заряд Q1 увеличился на dQ — величину столь малую, что в пределах изменения заряда напряжение можно считать неизменным:

Выражение энергии через характеристики электрического поля

Выражение (11.2) получено на основе закона сохранения энергии; однако из него непосредственно не следует, что энергия Wэ является энергией электрического поля. Можно показать, что эта энергия распределена в электрическом поле. Для примера рассмотрим равномерное электрическое поле плоского конденсатора (см. рис. 1.6, а).

Поток вектора электрического смещения через любую поверхность, проведенную в диэлектрике параллельно пластинам, равен заряду Q конденсатора, что следует из формулы (7.33): DS = Q. Напряженность равномерного электрического поля Е = U/l. Следовательно, где V — объем диэлектрика, в котором распределено поле, связанное с заряженными пластинами конденсатора. Отношение энергии к объему диэлектрика дает объемную плотность энергии электрического поля: Энергия, определенная формулой (11.2) через характеристики проводников, выражена также формулой (11.5) через характеристики электрического поля. Эквивалентность этих формул свидетельствует о том, что энергия системы заряженных тел является энергией электрического поля.

Задача 11.1.

Плоский воздушный конденсатор емкостью 600 пФ при расстоянии между электродами 2 см заряжен до напряжения U = 4 кВ и отключен от источника напряжения. Определить изменение энергии и напряженности электрического поля конденсатора при уменьшении расстояния между электродами вдвое. Решение. До изменения расстояния между обкладками энергия электрического поля, по формуле (11.3), Напряженность электрического поля [см. (1.5)] При уменьшении расстояния между обкладками вдвое емкость конденсатора согласно формуле (7.29) увеличивается вдвое. При этом заряд конденсатора не изменяется (предполагается, что утечки заряда нет). Вследствие увеличения емкости конденсатора напряжение между обкладками уменьшится во столько же раз [см. формулу (7.28)]: Энергия электрического поля Напряженность электрического поля

Механические силы в электрическом поле

Вопрос о механических силах в электрическом поле рассмотрим на примере плоского конденсатора, заряженного от внешнего источника энергии, имеющего напряжение U. Электрическое поле конденсатора будем полагать равномерным.

Энергетический баланс в электростатической системе

Силы Fэ, возникающие вследствие взаимодействия пластин с электрическим полем, приложены к пластинам и направлены так, что они притягиваются. Предположим, что одна из пластин конденсатора свободна, и возможное малое перемещение ее под действием силы Fэ обозначим через dх (рис. 11.2). Рис. 11.2. Механические силы в электрическом поле

В дальнейших рассуждениях будем исходить из того, что при изменении заряда конденсатора не возникает потерь энергии в проводниках в связи с перемещением заряженных частиц и в диэлектрике вследствие изменения напряженности поля.

При таких условиях в соответствии с законом сохранения энергии при изменении заряда конденсатора на dQ за счет энергии внешнего источника изменяется энергия электрического поля на dWэ и совершается механическая работа Fэdx:

Обобщенное выражение электрической силы (первый случай)

Заряд конденсатора остается неизменным (Q = const), т. е. заряженный конденсатор отключен от внешнего источника энергии. При dQ = 0 работа внешнего источника UdQ = 0. Поэтому или Последнее равенство показывает, что механическая работа, связанная с перемещением пластины, совершается за счет энергии электрического поля. Действительно, механическая работа, совершаемая электрической силой, положительна (Fэdх > 0), следовательно, изменение энергии электрического поля отрицательно (dWэ

Механическую силу, стремящуюся изменить положение пластины конденсатора, можно выразить отношением Рассуждая аналогично, можно получить зависимость между механическим моментом и углом поворота α, если механическое движение осуществляется в виде вращения одной пластины по отношению к другой: Изменение расстояния l между пластинами на dх изменит емкость конденсатора. При уменьшении расстояния емкость увеличивается, а напряжение между пластинами уменьшается, что непосредственно следует из формулы (7.28).

Предположим, что расстояние между пластинами увеличивается благодаря действию на пластины внешних механических сил. Энергия в системе возрастает на величину работы, совершенной внешним источником механической энергии. При этом емкость конденсатора уменьшится, а напряжение между пластинами увеличится.

Обобщенное выражение электрической силы (второй случай)

Напряжение между пластинами остается постоянным (U = const), т. е. во время движения пластины конденсатор не отключается от внешнего источника энергии.

При уменьшении расстояния между пластинами увеличивается емкость конденсатора, что при неизменном напряжении влечет за собой увеличение заряда.

Внешний источник энергии должен затратить энергию на увеличение заряда конденсатора в количестве UdQ.

Изменение энергии электрического поля dWэ при изменении заряда, согласно формуле (11.2), , т. е. составляет половину энергии внешнего источника, израсходованной при увеличении заряда конденсатора. Вторая половина энергии расходуется на покрытие механической работы Fэdх, следовательно, Отсюда Аналогично, при вращательном движении

Увеличение расстояния между пластинами в результате действия внешних механических сил приведет к уменьшению емкости. Но при постоянном напряжении за уменьшением емкости последуют уменьшение заряда конденсатора и уменьшение энергии электрического поля. В этом случае механическая работа, связанная с перемещением пластины, совершается внешними механическими силами. Величина этой работы численно равна уменьшению энергии электрического поля. Таким образом, источнику электрической энергии возвращается энергия, численно равная удвоенному значению механической работы.

ЭДС индукции

Каков механизм возникновения индукционного тока? Это мы обсудим позже. Пока ясно одно: при изменении магнитного потока, проходящего через контур, на свободные заряды в контуре действуют некоторые силы — сторонние силы

, вызывающие движение зарядов.

Как мы знаем, работа сторонних сил по перемещению единичного положительного заряда вокруг контура называется электродвижущей силой (ЭДС): . В нашем случае, когда меняется магнитный поток сквозь контур, соответствующая ЭДС называется ЭДС индукции

и обозначается .

Итак, ЭДС индукции — это работа сторонних сил, возникающих при изменении магнитного потока через контур, по перемещению единичного положительного заряда вокруг контура

.

Природу сторонних сил, возникающих в данном случае в контуре, мы скоро выясним.

Основные формулы для вычисления вектора МИ

Вектор магнитной индукции, формула которого B = Fm / I * ∆L, может быть найден с помощью других математических расчетов.

Закон электромагнитной индукции

Закон электромагнитной индукции (закон Фарадея) звучит так:

ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока на поверхности, ограниченной кольцом.

Математически это можно описать формулой:

Закон Фарадея Ɛi – индукционная ЭДС В ΔФ / Δt – скорость изменения магнитного потока Вт / с

Знак «-» в формуле позволяет учитывать направление индукционного тока. Индукционный ток в замкнутой цепи всегда направлен так, что магнитный поток поля, создаваемого этим током через поверхность, ограниченную кольцом, уменьшает те изменения поля, которые вызывают появление индукционного тока.

Если цепь состоит из N витков (т.е это катушка), ЭДС индукции будет рассчитываться следующим образом.

Закон Фарадея для цепи из N витков Ɛi – индукционная ЭДС В ΔФ / Δt – скорость изменения магнитного потока Вт / с N – количество оборотов

Сила индукционного тока в замкнутом токопроводящем контуре с сопротивлением R​:

Закон Ома для проводящей цепи Ɛi – индукционная ЭДС В I – сила индукционного тока [А] R – сопротивление цепи [Ом]

Если проводник длины l будет двигаться со скоростью v в постоянном однородном магнитном поле с индукцией B, ЭДС электромагнитной индукции будет равна:

Индукционная ЭДС для движущегося проводника Ɛi – индукционная ЭДС В B – магнитная индукция [Тл] v – скорость проводника [м / с] l – длина жилы [м]

Возникновение индукционного электромагнитного поля в проводнике, движущемся в магнитном поле, объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. В этом случае сила Лоренца играет роль внешней силы.

Проводник, движущийся в магнитном поле, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.

Количество тепла в цепи выделяется как за счет работы внешней силы, которая сохраняет скорость проводника неизменной, так и за счет уменьшения кинетической энергии проводника.

Изменение магнитного потока, попадающего в замкнутый контур, может происходить по двум причинам:

• из-за движения цепи или ее частей в постоянном магнитном поле с течением времени. Это тот случай, когда проводники, а вместе с ними и носители свободного заряда движутся в магнитном поле
• из-за изменения во времени магнитного поля с неподвижным контуром. В этом случае возникновение индукционной ЭДС уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея

Следовательно, явления индукции в подвижных и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока в этих двух случаях оказывается различной:

• в случае движущихся проводников ЭДС индукции возникает из-за силы Лоренца
• в случае неподвижных проводников ЭДС индукции является следствием действия вихревого электрического поля на свободные заряды, возникающего при изменении магнитного поля.

Закон Био-Савара-Лапласа

Формула индукции ЭДС

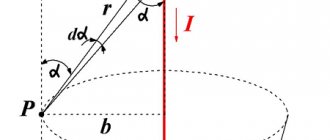
Описывает правила поиска B → магнитного поля, которое создает постоянный электрический ток. Это экспериментально установленная модель. Био и Савар в 1820 году показали это на практике, Лаплас смог его сформулировать. Этот закон является фундаментальным в магнитостатике. На практике рассматривался фиксированный провод малого сечения, по которому пропускался электрический ток. Для исследования был выбран небольшой участок проволоки, который характеризовался вектором dl. Его модуль соответствовал длине рассматриваемого участка, а направление совпадало с направлением тока.

Интересно. Лаплас Пьер Симон предложил также рассматривать движение электрона как ток и на этом утверждении с помощью этого закона доказал возможность определения МП наступающего точечного заряда.

Согласно этому физическому правилу каждый сегмент dl проводника, по которому протекает электрический ток I, образует магнитное поле dB в пространстве вокруг себя с интервалом r и под углом α:

дБ = µ0 * I * dl * sin α / 4 * π * r2,

где это находится:

• дБ – магнитная индукция, Тл;
• µ0 = 4 π * 10-7 – магнитная постоянная, Гн / м;
• I – сила тока, А;
• dl – отрезок жилы, м;
• r – расстояние от точки, где находится магнитная индукция, м;
• α – угол, образованный r и вектором dl.

Важно! Согласно закону Био-Савара-Лапласа, суммируя векторы магнитных полей отдельных секторов, можно определить МП требуемого тока. Он будет равен векторной сумме.

Закон Био-Савара-Лапласа

Существуют формулы, описывающие этот закон для отдельных случаев МП:

• поля прямого движения электронов;
• поля кругового движения заряженных частиц.

Формула депутата первого рода:

В = µ * µ0 * 2 * I / 4 * π * r.

Для кругового движения это выглядит так:

В = µ * µ0 * I / 4 * π * r.

В этих формулах µ – (относительная) магнитная проницаемость среды).

Рассматриваемый закон следует из уравнений Максвелла. Максвелл вывел два уравнения для МП, случай, когда электрическое поле постоянно, только что рассматривали Био и Савар.

Принцип суперпозиции

Для МП существует принцип, согласно которому полный вектор магнитной индукции в определенной точке равен векторной сумме всех векторов MI, созданных разными токами в данной точке:

B → = B1 → + B2 → + B3 →… + Bn→

Правило Ленца

Для определения направления индукционного тока необходимо использовать правило Ленца.

С академической точки зрения это правило звучит так: индукционный ток, возбуждаемый в замкнутой цепи при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле предотвращает изменение магнитного потока, вызывая индукционный ток.

Попробуем немного попроще: катушка в данном случае – недовольная бабушка. Они забирают магнитный поток: она несчастна и создает магнитное поле, которое этот магнитный поток хочет восстановить.

Они дают ей магнитный поток, они принимают его, они говорят, они используют его, и она такая – “Потому что ваш магнитный поток сдался мне!” и создает магнитное поле, которое вытесняет этот магнитный поток.

Закон электромагнитной индукции Фарадея

Сила индукционного тока в опытах Фарадея оказывалась тем больше, чем быстрее менялся магнитный поток через контур.

Если за малое время изменение магнитного потока равно , то скорость

изменения магнитного потока — это дробь (или, что тоже самое, производная магнитного потока по времени).

Опыты показали, что сила индукционного тока прямо пропорциональна модулю скорости изменения магнитного потока:

Модуль поставлен для того, чтобы не связываться пока с отрицательными величинами (ведь при убывании магнитного потока будет ). Впоследствии мы это модуль снимем.

Из закона Ома для полной цепи мы в то же время имеем: . Поэтому ЭДС индукции прямо пропорциональна скорости изменения магнитного потока:

(4)

ЭДС измеряется в вольтах. Но и скорость изменения магнитного потока также измеряется в вольтах! Действительно, из (3) мы видим, что Вб/с = В. Стало быть, единицы измерения обеих частей пропорциональности (4) совпадают, поэтому коэффициент пропорциональности — величина безразмерная. В системе СИ она полагается равной единице, и мы получаем:

(5)

Это и есть закон электромагнитной индукции

или
закон Фарадея
. Дадим его словесную формулировку.

Закон электромагнитной индукции Фарадея

.
При изменении магнитного потока, пронизывающего контур, в этом контуре возникает ЭДС индукции, равная модулю скорости изменения магнитного потока
.

Контур с током и катушка индуктивности

Контур с током может быть одиночным (одновитковая катушка)

Контур с током может состоять из нескольких контуров (многовитковая катушка)

В электротехнике и радиотехнике применяются многовитковые катушки.

Чем больше витков, тем больше индуктивность катушки. Один и тот же ток, протекающий через одиночный виток и через многовитковую катушку, создаст разное по силе магнитное поле. У многовитковой катушки индуктивность больше, чем у одного витка; она пропорциональна количеству витков.

Когда нужно создать сильное магнитное поле, наматывают сотни и тысячи витков из тонкой медной проволоки. Такие катушки применяются в электромагнитах, трансформаторах, электродвигателях.

Правило Ленца

Магнитный поток, изменение которого приводит к появлению индукционного тока в контуре, мы будем называть внешним магнитным потоком

. А само магнитное поле, которое создаёт этот магнитный поток, мы будем называть
внешним магнитным полем
.

Зачем нам эти термины? Дело в том, что индукционный ток, возникающий в контуре, создаёт своё собственное

магнитное поле, которое по принципу суперпозиции складывается с внешним магнитным полем.

Соответственно, наряду с внешним магнитным потоком через контур будет проходить собственный

магнитный поток, создаваемый магнитным полем индукционного тока.

Оказывается, эти два магнитных потока — собственный и внешний — связаны между собой строго определённым образом.

Правило Ленца

.
Индукционный ток всегда имеет такое направление, что собственный магнитный поток препятствует изменению внешнего магнитного потока
.

Правило Ленца позволяет находить направление индукционного тока в любой ситуации.

Рассмотрим некоторые примеры применения правила Ленца.

Предположим, что контур пронизывается магнитным полем, которое возрастает со временем (рис. (3)). Например, мы приближаем снизу к контуру магнит, северный полюс которого направлен в данном случае вверх, к контуру.

Магнитный поток через контур увеличивается. Индукционный ток будет иметь такое направление, чтобы создаваемый им магнитный поток препятствовал увеличению внешнего магнитного потока. Для этого магнитное поле, создаваемое индукционным током, должно быть направлено против

внешнего магнитного поля.

Индукционный ток течёт против часовой стрелки, если смотреть со стороны создаваемого им магнитного поля. В данном случае ток будет направлен по часовой стрелке, если смотреть сверху, со стороны внешнего магнитного поля, как и показано на (рис. (3)).

Рис. 3. Магнитный поток возрастает

Теперь предположим, что магнитное поле, пронизывающее контур, уменьшается со временем (рис. 4). Например, мы удаляем магнит вниз от контура, а северный полюс магнита направлен на контур.

Рис. 4. Магнитный поток убывает

Магнитный поток через контур уменьшается. Индукционный ток будет иметь такое направление, чтобы его собственный магнитный поток поддерживал внешний магнитный поток, препятствуя его убыванию. Для этого магнитное поле индукционного тока должно быть направлено в ту же сторону

, что и внешнее магнитное поле.

В этом случае индукционный ток потечёт против часовой стрелки, если смотреть сверху, со стороны обоих магнитных полей.

Как формулируется правило ленца

ПРАВИЛО ЛЕНЦА — ПРАВИЛО ЛЕНЦА, электромагнитный закон, выведенный русским физиком Генрихом Ленцем (1804 65) в 1834 г. Закон гласит, что индуцированный электрический ток течет в направлении, противоположном заряду, который произвел этот ток. см. также ИНДУКЦИЯ … Научно-технический энциклопедический словарь

правило Ленца — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN law of induced currentLenz s lawLenz s rule … Справочник технического переводчика

правило Ленца — правило, определяющее направление индукционных токов (возникающих при электромагнитной индукции); следствие закона сохранения энергии. Согласно правилу Ленца возникающий в замкнутном контуре индукционный ток направлен так, что… … Энциклопедический словарь по металлургии

правило Ленца — Lenco taisyklė statusas T sritis fizika atitikmenys: angl. Lenz’s law; Lenz’s rule vok. Lenzsche Regel, f; Lenzsches Gesetz, n rus. закон Ленца, m; правило Ленца, n pranc. loi de Lenz, f … Fizikos terminų žodynas

ЛЕНЦА ПРАВИЛО — определяет направление пндукц. токов, возникающих в результате электромагнитной индукции; является следствием закона сохранения энергии. Л. п. установлено (1833) Э. X. Ленцем. Индукц. ток в контуре направлен так, что создаваемый им поток… … Физическая энциклопедия

• ПРАВИЛО — (1) буравчика определяет направление вектора напряжённости магнитного поля прямолинейного проводника с постоянным током. Если буравчик ввёртывается по направлению тока, то направление его вращения определяет направление магнитных силовых линий… … Большая политехническая энциклопедия
• Ленца правило — Правило Ленца, правило для определения направления индукционного тока: Индукционный ток, возникающий при относительном движении проводящего контура и источника магнитного поля, всегда имеет такое направление, что его собственный магнитный поток… … Википедия
• правило правой руки — удобное для запоминания правило для определения направления индукционного тока в проводнике, движущегося в магнитном поле: если расположить правую ладонь так, чтобы отставлtysq большой палец совпадал с направлением движения… … Энциклопедический словарь по металлургии

Ковролин ламинат или линолеум что лучше

1. правило фаз — уравнение, связывающее число степеней свободы (С) термодинамической системы с числом компонентов (К) и числом равновесных фаз (Ф): С = К Ф + 2. Если влиянием давления на фазовое равновесие можно пренебречь, то правило фаз имеет вид:… … Энциклопедический словарь по металлургии
2. правило рычага — , правило отрезков одно из проявлений закона сохранения массы вещества, устанавливающего взаимосвязь между химическими составами и массами двух веществ и 3 го вещества, образованного из первых двух; служит для определения по диаграмме … Энциклопедический словарь по металлургии
3. Весь мир в твоих руках — все будет так, как ты захочешь

Взаимодействие магнита с контуром

Итак, приближение или удаление магнита приводит к появлению в контуре индукционного тока, направление которого определяется правилом Ленца. Но ведь магнитное поле действует на ток! Появится сила Ампера, действующая на контур со стороны поля магнита. Куда будет направлена эта сила?

Если вы хотите хорошо разобраться в правиле Ленца и в определении направления силы Ампера, попробуйте ответить на данный вопрос самостоятельно. Это не очень простое упражнение и отличная задача для С1 на ЕГЭ. Рассмотрите четыре возможных случая.

1. Магнит приближаем к контуру, северный полюс направлен на контур. 2. Магнит удаляем от контура, северный полюс направлен на контур. 3. Магнит приближаем к контуру, южный полюс направлен на контур. 4. Магнит удаляем от контура, южный полюс направлен на контур.

Не забывайте, что поле магнита не однородно: линии поля расходятся от северного полюса и сходятся к южному. Это очень существенно для определения результирующей силы Ампера. Результат получается следующий.

Если приближать магнит, то контур отталкивается от магнита. Если удалять магнит, то контур притягивается к магниту. Таким образом, если контур подвешен на нити, то он всегда будет отклоняться в сторону движения магнита, словно следуя за ним. Расположение полюсов магнита при этом роли не играет

.

Уж во всяком случае вы должны запомнить этот факт — вдруг такой вопрос попадётся в части А1

Результат этот можно объяснить и из совершенно общих соображений — при помощи закона сохранения энергии.

Допустим, мы приближаем магнит к контуру. В контуре появляется индукционный ток. Но для создания тока надо совершить работу! Кто её совершает? В конечном счёте — мы, перемещая магнит. Мы совершаем положительную механическую работу, которая преобразуется в положительную работу возникающих в контуре сторонних сил, создающих индукционный ток.

Итак, наша работа по перемещению магнита должна быть положительна

. Это значит, что мы, приближая магнит, должны
преодолевать
силу взаимодействия магнита с контуром, которая, стало быть, является силой
отталкивания
.

Теперь удаляем магнит. Повторите, пожалуйста, эти рассуждения и убедитесь, что между магнитом и контуром должна возникнуть сила притяжения.

Энергия магнитного поля

Магнитное поле обладает энергией. Магнитные силы совершают механическую работу, притягивая или отталкивая другие магниты или тела из магнитных материалов. Меняющееся магнитное поле индуцирует электрический ток в проводниках.

Магнитную энергию можно выразить через математическую формулу. В предыдущем разделе упоминалась инерционность индуктивной цепи, ее роль в электромагнитных явлениях сравнивалась с ролью массы в механике. Интересно, что эта аналогия углубляется при рассмотрении энергии.

Формула энергии магнитного поля похожа на формулу кинетической энергии механического тела:

Энергия магнитного поля пропорциональна индуктивности и квадрату величины тока.

Во время переходного процесса, когда при включении ток в цепи замедленно нарастает, происходит накопление магнитной энергии. Эта энергия может использоваться для совершения работы. И эта энергия создает проблемы при выключении тока в цепи с большой индуктивностью.

Если ток уменьшать, возникнет ЭДС, замедляющая уменьшение тока. Но если ток выключить, резко разорвав цепь, скорость изменения тока от конкретного значения до нуля теоретически должна быть бесконечно велика. Это значит, ЭДС самоиндукции при выключении тока тоже должна быть бесконечно велика.

Этот математический парадокс возник из-за упрощенных идеализированных формул. В реальности ток не прекращается мгновенно, размыкание контактов занимает некоторый короткий промежуток времени, но все равно скорость изменения тока велика, и наводится ЭДС значительной величины. Обычным явлением при выключении цепи является искрение. Если выключать ток в цепи с большой индуктивностью, то попытка резкого прекращения тока может стать причиной вспышки электрической дуги.

Что произойдет, если дуга не вспыхнула, а ток прекратился? Куда девалась энергия магнитного поля? Частично она перешла в тепловую энергию – контакты выключателя нагрелись. Остальная часть энергии магнитного поля, при его резком уменьшении до нуля, перешла в электромагнитную волну. Переменное магнитное поле индуцировало переменное электрическое поле; в свою очередь, переменное электрическое вызвало новую волну магнитного, и так далее.

Выключение тока простым щелчком выключателя – посылает в бесконечное пространство широкий «шумовой» спектр электромагнитных колебаний.

Закон Фарадея + Правило Ленца = Снятие модуля

Выше мы обещали снять модуль в законе Фарадея (5). Правило Ленца позволяет это сделать. Но сначала нам нужно будет договориться о знаке ЭДС индукции — ведь без модуля, стоящего в правой части (5), величина ЭДС может получаться как положительной, так и отрицательной.

Прежде всего, фиксируется одно из двух возможных направлений обхода контура. Это направление объявляется положительным

. Противоположное направление обхода контура называется, соответственно,
отрицательным
. Какое именно направление обхода мы берём в качестве положительного, роли не играет — важно лишь сделать этот выбор.

Магнитный поток через контур считается положительным , если магнитное поле, пронизывающее контур, направлено туда, глядя откуда обход контура в положительном направлении совершается против часовой стрелки. Если же с конца вектора магнитной индукции положительное направление обхода видится по часовой стрелке, то магнитный поток считается отрицательным .

ЭДС индукции считается положительной , если индукционный ток течёт в положительном направлении. В этом случае направление сторонних сил, возникающих в контуре при изменении магнитного потока через него, совпадает с положительным направлением обхода контура.

Наоборот, ЭДС индукции считается отрицательной , если индукционный ток течёт в отрицательном направлении. Сторонние силы в данном случае также будут действовать вдоль отрицательного направления обхода контура.

Итак, пусть контур находится в магнитном поле . Фиксируем направление положительного обхода контура. Предположим, что магнитное поле направлено туда, глядя откуда положительный обход совершается против часовой стрелки. Тогда магнитный поток положителен: .

Предположим, далее, что магнитный поток увеличивается . Согласно правилу Ленца индукционный ток потечёт в отрицательном направлении (рис. 5).

Рис. 5. Магнитный поток возрастает

Стало быть, в данном случае имеем . Знак ЭДС индукции оказался противоположен знаку скорости изменения магнитного потока. Проверим это в другой ситуации.

А именно, предположим теперь, что магнитный поток убывает . По правилу Ленца индукционный ток потечёт в положительном направлении. Стало быть, (рис. 6).

Рис. 6. Магнитный поток возрастает

Таков в действительности общий факт: при нашей договорённости о знаках правило Ленца всегда приводит к тому, что знак ЭДС индукции противоположен знаку скорости изменения магнитного потока

:

(6)

Тем самым ликвидирован знак модуля в законе электромагнитной индукции Фарадея.

Магнитная индукция

Согласно прогрессивным научным представлениям об электрических явлениях, МП неразрывно связан с током и не может присутствовать без него. Невозможно предположить электроток без МП. В том числе в случае неизменного магнита связывают этот фон с молекулярными линиями.

Если в место, где находится МП, поставить иглу, она стремится заимствовать определённое состояние, которое фактически показывает ориентационные качества МП. Скоординированное направление в этой точке места должно учитывать пункт назначения, где установлена ось, — это свободноподвешенная бесконечно небольшая магнитная стрелка, середина которой выровнена с точкой начального места. При этом из 2 возможных направлений вдоль оси стрелки МП символически присваивается назначение от южного конца на север.

Можно получить более яркое представление о направленности поля, если имеется ряд линий, где оси всех стрелок будут относительно касательными. Эти части называются магнитными магистралями.

Набор рядов упоминается как МП. Если бесконечно уменьшать площадь контура, притягивая его к точке, можно прийти к выражению для бесконечно малой стадии d, T активно в контуре маленькой области s, где угол P имеет конкретное значение между нормальностью к плоскости и небольшого контура. В этом случае направлением поля будет точка места, где расположено малое очертание.

Вихревое электрическое поле

Рассмотрим неподвижный контур, находящийся в переменном магнитном поле. Каков же механизм возникновения индукционного тока в контуре? А именно, какие силы вызывают движение свободных зарядов, какова природа этих сторонних сил?

Пытаясь ответить на эти вопросы, великий английский физик Максвелл открыл фундаментальное свойство природы: меняющееся во времени магнитное поле порождает поле электрическое

. Именно это электрическое поле и действует на свободные заряды, вызывая индукционный ток.

Линии возникающего электрического поля оказываются замкнутыми, в связи с чем оно было названо вихревым электрическим полем

. Линии вихревого электрического поля идут вокруг линий магнитного поля и направлены следующим образом.

Пусть магнитное поле увеличивается. Если в нём находится проводящий контур, то индукционный ток потечёт в соответствии с правилом Ленца — по часовой стрелке, если смотреть с конца вектора . Значит, туда же направлена и сила, действующая со стороны вихревого электрического поля на положительные свободные заряды контура; значит, именно туда направлен вектор напряжённости вихревого электрического поля.

Итак, линии напряжённости вихревого электрического поля направлены в данном случае по часовой стрелке (смотрим с конца вектора , (рис. 7).

Рис. 7. Вихревое электрическое поле при увеличении магнитного поля

Наоборот, если магнитное поле убывает, то линии напряжённости вихревого электрического поля направлены против часовой стрелки (рис. 8).

Рис. 8. Вихревое электрическое поле при уменьшении магнитного поля

Теперь мы можем глубже понять явление электромагнитной индукции. Суть его состоит именно в том, что переменное магнитное поле порождает вихревое электрическое поле. Данный эффект не зависит от того, присутствует ли в магнитном поле замкнутый проводящий контур или нет; с помощью контура мы лишь обнаруживаем это явление, наблюдая индукционный ток.

Вихревое электрическое поле по некоторым свойствам отличается от уже известных нам электрических полей: электростатического поля и стационарного поля зарядов, образующих постоянный ток.

1. Линии вихревого поля замкнуты, тогда как линии электростатического и стационарного полей начинаются на положительных зарядах и оканчиваются на отрицательных. 2. Вихревое поле непотенциально: его работа перемещению заряда по замкнутому контуру не равна нулю. Иначе вихревое поле не могло бы создавать электрический ток! В то же время, как мы знаем, электростатическое и стационарное поля являются потенциальными.

Итак, ЭДС индукции в неподвижном контуре — это работа вихревого электрического поля по перемещению единичного положительного заряда вокруг контура

.

Пусть, например, контур является кольцом радиуса и пронизывается однородным переменным магнитным полем. Тогда напряжённость вихревого электрического поля одинакова во всех точках кольца. Работа силы , с которой вихревое поле действует на заряд , равна:

Следовательно, для ЭДС индукции получаем:

Проведен точный эксперимент по измерению персистентного тока в металлическом кольце

Рис. 1.

Магнитный поток в металлическом кольце с диаметром порядка 1 мкм индуцирует персистентный ток. При температуре около 1 К величина тока составляет приблизительно 1 нА (наноампер). Направление тока выбрано произвольным образом. Рисунок Ю. Ерина

В 1983 году физики-теоретики высказали гипотезу, согласно которой магнитный поток, пронизывающий металлическое кольцо диаметром около 1 мкм, должен создавать незатухающий ток — так называемый персистентный ток. Причины его возникновения не имеют ничего общего со сверхпроводимостью и кроются в квантовых особенностях движения некоторых электронов в металле. Было предложено несколько теорий персистентного тока, предсказывающих его величину и направление. Однако маленькая величина такого незатухающего тока не позволяет аккуратно измерить его значение и сравнить с существующими теоретическими моделями. Группе американских и немецких ученых, благодаря их оригинальной экспериментальной установке, впервые удалось очень точно измерить величину персистентного тока в металлическом кольце. Их результат должен помочь физикам выявить правильную модель описания данного явления.

Что такое сопротивление?

Всем известно, что электрический ток в веществе — это направленное движение свободных заряженных частиц. В металле ток создается свободными электронами — электронами, находящимися на самых далеких орбитах атома и слабо связанными с атомным ядром. Чтобы возникло направленное движение, необходимо на концах проводника создать разность потенциалов или напряжение. Вызванное напряжением электрическое поле в металле заставляет электроны диффундировать в нём. Движущиеся заряженные частицы сталкиваются, теряют часть своей энергии и рассеиваются на ионах, различных дефектах, неоднородностях кристаллической решетки и примесях в веществе. Такое диссипативное (то есть сопровождающееся уменьшением энергии) рассеяние и приводит к возникновению сопротивления.

Если электроны рассматривать как частицы, подчиняющиеся в своем движении классическим законам физики, то, записав второй закон Ньютона, можно получить математическую взаимосвязь между плотностью тока, идущего через металл, и электрическим напряжением, вызывающим его протекание. Проще говоря, можно теоретически вывести экспериментальный закон Ома. Именно так в начале XX века Пауль Друде получил теорию электронной проводимости металлов и, в частности, знаменитую формулу для сопротивления, названную его именем (см. Теория Друде). Одними из главных характеристик в теории Друде были длина и время свободного пробега электронов в металле между столкновениями с «помехами». Поскольку формула Друде неплохо описывала сопротивление проводников, то она практически не изменилась даже тогда, когда появилась квантовая механика.

В 70-е годы было открыто отрицательное магнитосопротивление — уменьшение сопротивления проводника при увеличении индукции магнитного поля. Это открытие никак не укладывалась в рамки теории Друде. В 1979 году американские и советские физики установили, что к классической формуле сопротивления необходимо добавить слагаемое, связанное с квантовым поведением электрона, поскольку электрон, согласно известному принципу дуализма, не только частица, но и волна. Иными словами, сопротивление надо объяснять не только столкновением частиц, но и учитывать так называемые эффекты квантовой интерференции электронных волн.

Через год Борис Альтшулер с коллегами построил количественную теорию этого явления, объяснившую, в частности, отрицательное магнитосопротивление. В их статье, помимо уже известных классических величин, таких как время и длина свободного пробега электронов, появились новые характеристики для описания сопротивления — время и длина фазовой когерентности электронов. Длина фазовой когерентности — это расстояние бездиссипативного рассеяния электрона, то есть дистанция, которую преодолевает электронная волна или электрон, не испытав неупругого рассеяния (не утратив первоначальную энергию). Время фазовой когерентности — это время между неупругими столкновениями электрона, или время, в течение которого электронная волна не теряет свою энергию. Из определения следует, что на такой длине электрон дает нулевой вклад в общее сопротивление металла.

Понижение температуры подавляет вероятность неупругого столкновения электронной волны и, соответственно, вероятность уменьшения энергии электрона, отражающегося на макроскопическом уровне в виде снижения сопротивления. Следовательно, чем меньше температура, тем больше время и длина фазовой когерентности. Например, при температуре жидкого гелия (около 4 К) масштаб фазовой когерентности составляет примерно один микрометр для многих металлов.

У читателя может возникнуть вопрос: так чем же друдевская длина свободного пробега электрона отличается от длины фазовой когерентности, которая на первый взгляд имеет такой же физический смысл? Всё дело в том, что в классической теории совершенно не важно, упруго или нет электрон сталкивается с ионом, дефектом и т. п. Любое рассеяние электрона трактуется как событие, приводящее к увеличению сопротивления вещества. При квантовом подходе электроны в пределах длины фазовой когерентности упруго сталкиваются с препятствиями на своем пути и не меняют свою энергию до некоторого момента, пока вероятность неупругого столкновения с помехой не станет значительной.

Персистентные токи и причины их возникновения

На квантовые поправки к сопротивлению в 1983 году обратили внимание физики Рольф Ландауэр, Маркус Бюттикер и Йозеф Имри, опубликовавшие в журнале Physics Letters A

интересную гипотезу. Что будет, если взять металлическую проволоку с длиной и площадью поперечного сечения меньшей или равной длине фазовой когерентности, замкнуть ее в кольцо, охладить до низких температур и потом пронизать магнитным потоком (рис. 1)?

Ученые пришли к выводу, что в таком кольце начнут течь незатухающие токи, не имеющие ничего общего с токами в сверхпроводниках. Их назвали персистентными токами (от англ. persistent

«постоянный»). Магнитное поле здесь играет важную роль. Дело в том, что электроны с равной вероятностью двигаются в кольце либо по часовой стрелке, либо против, то есть в среднем ток в кольце равен нулю. Разрушить эту симметрию и задать конкретное направление движению электронов — главная задача магнитного поля.

Заметим, что различия между сверхпроводящими и персистентными токами весьма существенны. Как уже было сказано, электрон может двигаться без сопротивления в пределах длины фазовой когерентности. В сверхпроводнике за счет объединения электронов в пары, а точнее, в куперовские пары, их длина и время фазовой когерентности равны бесконечности. Они перемещаются без сопротивления сколь угодно долго и на сколь угодно большое расстояние. Более того, сверхпроводящий ток создают абсолютно все электроны проводимости металла.

В случае с персистентным током никакого объединения частиц в пары не происходит. Персистентный ток создают лишь те электроны, для которых существует наибольшая вероятность беспрепятственного перемещения в пределах длины фазовой когерентности. Некоторые частицы даже в пределах фазовой когерентности не в состоянии двигаться без потерь своей энергии. Понижая температуру, мы не только увеличиваем длину фазовой когерентности, но и увеличиваем вероятность бездиссипативного прохождения через препятствия для большего количества электронов. Однако всё равно остаются частицы, для которых эта задача непреодолима.

Описанное явление кажется невероятным, но давайте вспомним, что движение электрона вокруг атомного ядра тоже можно интерпретировать как незатухающий ток. Грубо говоря, аналогичная картина наблюдается и в металлическом кольце.

На макроскопическом уровне разница между этими двумя видами токов проявляется в том, что величина текущего персистентного тока не зависит от площади поперечного сечения кольца. Более того, сверхпроводящий ток в кольце с такими же размерами будет намного больше персистентного тока в нём. Интересно отметить здесь еще и тот факт, что персистентный ток существует в кольце, которое фактически обладает сопротивлением. Ничто не мешает подключить к кольцу источник питания и тем самым заставить течь по нему ток. Просто общий ток будет суммой или разностью обычного тока, идущего от батарейки, и персистентного тока (всё зависит от направления протекания обычного тока).

Чудеса на этом не заканчиваются. Теоретики, помимо всего прочего, показали, что значение персистентного тока осциллирует в зависимости от магнитного потока, пронизывающего кольцо. Период таких колебаний равен отношению двух фундаментальных констант — постоянной Планка h

и заряда электрона
e
(
h
/
e
= 4,1·10–15 Тл·м2). В физике отношение
h
/
e
называют квантом магнитного потока —
флюксоидом
(в сверхпроводимости флюксоид в 2 раза меньше:
h
/
2e
; двойка возникает из-за объединения электронов в куперовские пары). Максимальное значение персистентного тока (максимальная амплитуда) будет наблюдаться, когда магнитный поток через кольцо составляет целое число флюксоидов. Если же магнитный поток кратен половине флюксоида, то персистентный ток не возникнет.

Несмотря на то что причины возникновения персистентных токов уже не подвергаются сомнению, теория этих токов до конца пока что так и не построена. Во-первых, нет четкой формулы, определяющей величину персистентного тока в кольце. Во-вторых, хотя и ясно, что направление протекания тока зависит от количества электронов, участвующего в этом движении, теоретики не могут точно предсказать, в какую сторону он потечет. Всё основывается лишь на приблизительных оценках. Так, для температуры 1 К в кольце диаметром около 1 мкм (это соответствует длине фазовой когерентности при температуре 1 К) амплитуда персистентного тока должна иметь значение порядка одного наноампера (10–9 А).

К настоящему времени выдвинуто несколько правдоподобных теоретических моделей, описывающих данный эффект. Каждая из них предсказывает периодичность по магнитному потоку и каждая дает результаты, совпадающие по порядку величины с вышеприведенным 10–9 А. Но все модели сильно различаются в числе перед степенью 10–9. Поэтому узнать, какая из теорий количественно верно описывает явление персистентного тока, можно лишь проведя эксперименты по наиболее точному измерению его величины.

Хотелось бы подчеркнуть, что причины, вызывающие возникновение персистентных токов, имеют исключительно квантовую природу. Это относится и к магнитному потоку, пронизывающему кольцо. «Классическое» влияние магнитного поля в виде силы Лоренца, действующей на все движущиеся заряженные частицы, несущественно. Не вдаваясь в подробности, приведем такой наглядный пример. Пусть магнитный поток через кольцо диаметром порядка 1 мкм создается с помощью длинного соленоида диаметром, скажем, 0,5 мкм. Его расположение таково, что плоскость кольца перпендикулярна оси соленоида и пересекает его середину. За пределами соленоида индукция равна нулю, и магнитное поле фактически не влияет на кольцо. Так было бы в классической физике. Однако согласно квантовой механике, динамика электронов обусловлена не индукцией поля, а его так называемым векторным потенциалом, который вне соленоида нулю никак не равен. Вообще говоря, описанная здесь ситуация известна в физике как пример проявления эффекта Ааронова–Бома. Таким образом, можно сказать, что появление персистентных токов в кольце обусловлено двумя причинами — фазовой когерентностью электронов и эффектом Ааронова–Бома.

Эксперименты по наблюдению и измерению персистентных токов

В первой части новости было сказано, что при очень низкой температуре длина фазовой когерентности равна приблизительно 1 мкм. Значит, изготовив кольцо с длиной окружности около микрометра и охладив его до гелиевых температур, можно наблюдать и измерять незатухающий персистентный ток.

Однако, как это часто бывает, возникли проблемы технического плана. Прежде всего, металл не должен быть сверхпроводящим при низкой температуре. Такие материалы есть — это золото, медь и серебро, — так что в принципе вопрос с материалом решается. Другая проблема — в невозможности непосредственно впаять в кольцо амперметр, да еще и микроскопических размеров, чтобы измерить персистентный ток. Таких амперметров просто нет, да и сила тока настолько мала (около 1 нА), что находится вне измерительного диапазона самых точных измерительных приборов такого класса. Тогда ученые пошли другим путем. Измерить возникающий незатухающий ток можно посредством специальных, очень чувствительных магнитометров — СКВИДов (SQUID). По зарегистрированной величине магнитного поля, создаваемого персистентными токами, затем легко восстановить значение тока, соответствующее наблюдаемому полю.

Используя эту методику, группа ученых из Белловской лаборатории во главе с Лораном Леви — спустя 7 лет после выхода в свет работы Бюттикера, Ландауэра и Имри — провела в 1990 году первый эксперимент по наблюдению и измерению персистентных токов на массиве (около 100 тыс. штук) небольших, приблизительно 0,5 мкм в диаметре, медных колец (см. L. P. Lévy, G. Dolan, J. Dunsmuir, H. Bouchiat. Magnetization of mesoscopic copper rings: Evidence for persistent currents // Phys. Rev. Lett.

64, 2074–2077). Результат оказался неутешительным: персистентные токи есть, они действительно зависят от магнитного потока через кольца, и их величина осциллирует с периодом равным одному флюксоиду. Но точно измерить их величину оказалось не под силу даже СКВИДу — чувствительность магнитометра группы Леви была на уровне измеряемой величины. К тому же возникали сильные помехи из-за магнитных примесей в веществе, всегда присутствующих даже в очень чистом кольце.

Позже были предприняты новые попытки, под руководством других ученых, измерить персистентные токи с помощью всё тех же СКВИДов, однако во всех экспериментах разброс данных был так велик, что часто разнился на порядки. Единственным достижением было подтверждение наличия колебаний тока с периодом h/e

. Стало ясно, что инструментальная погрешность существующих магнитометров не позволяет точно измерить наблюдаемый эффект.

И вот недавно в журнале Science

появилась совместная статья американских и немецких ученых Persistent Currents in Normal Metal Rings, оригинальным образом исследовавших персистентные токи в массивах алюминиевых колец с диаметром около 1 мкм. Предложенная ими конструкция позволяет измерить величину персистентных токов с беспрецедентной точностью — в 250 раз точнее, чем это удавалось с помощью СКВИД-магнитометров. Впервые точность измерения персистентных токов оказалась достаточной для проверки правильности существующих теоретических моделей.

Экспериментальная установка авторов статьи представляла собой кремниевую пластину — кантилевер, — на которой литографическим образом (см. Электронная литография) было нанесено 1680 колец с одинаковых диаметром 308 нм (рис. 2). Вся система охлаждалась до температуры ниже 1 К и помещалась в магнитное поле порядка 1 Тл (такая огромная величина магнитной индукции не позволяла кольцам переходить в сверхпроводящее состояние при данной температуре, несмотря на то что алюминий становится сверхпроводником уже при 1,2 К).

Рис. 2.

Схема экспериментальной установки авторов статьи.
A
— на пластине из монокристаллического кремния (на кантилевере) литографическим образом нанесен массив из одинаковых алюминиевых колец. Кантилевер охлажден до температуры ниже 1 К. Под некоторым углом Θ приложено магнитное поле. Компонента магнитного поля, которая перпендикулярна плоскости пластины, генерирует персистентные токи в кольцах. Параллельная составляющая магнитного поля создает вращательный момент кантилевера, который в свою очередь изменяет первоначальную (до возникновения магнитного поля) частоту свободных колебаний. Так как вращательный момент, помимо индукции магнитного поля, зависит также и от силы персистентных токов, то, измерив сдвиг частоты, можно определить их значение для заданной индукции поля.
B
и
C
— изображения кантилеверов и массива металлических колец на них, полученные с помощью сканирующего электронного микроскопа (
C
— увеличенное изображение участка, отмеченного
красным прямоугольником
на
B
). Из обсуждаемой статьи в
Science
Пластина располагалась под некоторым углом по отношению к силовым линиям магнитного поля. Компонента магнитного поля, перпендикулярная пластине, индуцировала персистентный ток. Одновременно с этим параллельная составляющая придавала кантилеверу вращательный момент. Сам по себе вращательный момент есть произведение нескольких величин — уже упомянутой индукции магнитного поля, суммарной силы тока колец, их площадью и углом между силовыми линиями и воображаемым перпендикуляром к кантилеверу. Если бы угол его наклона к силовым линиям был равен нулю, то никакого персистентного тока в кольцах не возникло бы, так как магнитный поток через кольца был бы равен нулю. Очевидно, что чем больше наклон кантилевера, тем больший ток течет по кольцам. Казалось бы, выгодно расположить пластину с кольцами перпендикулярно к силовым линиям, однако такая конфигурация создает нулевой вращательным момент кантилевера и не дает возможности измерить ток.

Кантилевер, как и любое другое тело, имеет характерную частоту свободных колебаний. Вращательный момент изменяет характерную частоту колебаний. Памятуя об этом и о том, что вращательный момент зависит также от силы тока в кольцах, авторы меняли индукцию магнитного поля и фиксировали лазером новую частоту свободных колебаний кантилевера. По отклонению частоты колебаний от первоначального значения ученые рассчитывали суммарный персистентный ток колец. Поскольку кольца в массиве совершенно одинаковые, то легко определить ток в единичном кольце. Результаты всех своих измерений ученые представили в виде графических зависимостей величины персистентного тока одного кольца от индукции магнитного поля (рис. 3) для разных углов наклона кремниевой пластины.

Рис. 3.

Зависимость персистентного тока одного алюминиевого кольца от индукции магнитного поля, приложенного к массиву из колец с диаметром 308 нм при температуре 365 мК и углом Θ = 45° (
A
), для массива из колец с диаметром 418 нм при температуре 365 мК и Θ = 45° (
B
) и для массива из колец с диаметром 793 нм при температуре 323 мК и Θ = 6° (
C
). На всех графиках период осцилляций соответствует магнитному потоку одного флюксоида. На рисунках
A
и
B
ток измеряется в наноамперах, на
C
— в пикоамперах (10–12 A). Изображения из обсуждаемой статьи в
Science
На каждой из кривых легко усматривается осциллирующий характер зависимости персистентного тока от индукции магнитного поля. Период осцилляций соответствует, как и предсказывает теория, магнитному потоку одного флюксоида, то есть 4,05·10–15 Тл·м2.

В заключение хотелось бы сказать об огромной — без преувеличения — важности статьи американских и немецких исследователей. Физики-теоретики наконец получили возможность сравнить свои модели с точными экспериментальными данными, выяснив заодно, какая из теорий персистентных токов наиболее правильно их описывает.

Источник:

A. C. Bleszynski-Jayich, W. E. Shanks, B. Peaudecerf, E. Ginossar, F. von Oppen, L. Glazman, J. G. E. Harris. Persistent Currents in Normal Metal Rings //
Science
. 9 October 2009. V. 326. P. 272–275.

Юрий Ерин

Магнитное поле Земли

Нашу планету можно представить в виде магнита, ось которого наклонена на 12 градусов. Пересечения этой оси с поверхностью называют магнитными полюсами. Как и у любого магнита, силовые линии Земли идут от северного полюса к южному. Возле полюсов они проходят перпендикулярно поверхности, поэтому там стрелка компаса ненадёжна, и приходится использовать другие способы.

Частицы «солнечного ветра» имеют электрический заряд, поэтому при движении вокруг них появляется магнитное поле, взаимодействующее с полем Земли и направляющее эти частицы вдоль силовых линий. Тем самым это поле защищает земную поверхность от космической радиации. Однако возле полюсов эти линии направлены перпендикулярно поверхности, и заряженные частицы попадают в атмосферу, вызывая северное сияние.

Электромагниты

Формула силы тока

В 1820 году Ганс Эрстед, проводя эксперименты, увидел воздействие проводника, по которому протекает электрический ток, на стрелку компаса. Через несколько дней Андре-Мари Ампер обнаружил взаимное притяжение двух проводов, по которым протекал ток одного направления.

Интересно. Во время электросварочных работ рядом расположенные кабеля двигаются при изменении силы тока.

Позже Ампер предположил, что это связано с магнитной индукцией тока, протекающего по проводам.

В катушке, намотанной изолированным проводом, по которому протекает электрический ток, поля отдельных проводников усиливают друг друга. Для увеличения силы притяжения катушку наматывают на незамкнутом стальном сердечнике. Этот сердечник намагничивается и притягивает железные детали или вторую половину сердечника в реле и контакторах.

Правило правой руки

При движении проводника в магнитном поле в нём наводится ЭДС. Её направленность зависит от направления движения провода. Метод, при помощи которого определяется направление магнитной индукции, называется «метод правой руки».

Расчёт величины магнитного поля важен для проектирования электрических машин и трансформаторов.