Как обозначается индукция магнитного поля в физике? Формула и теория

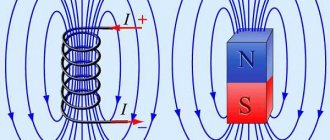
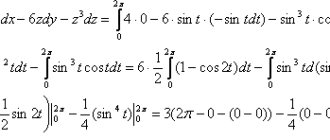Физический смысл магнитной индукции (МИ)

Возможность действовать на предмет магнитным полем (МП) определяет сущность настоящей индукции. Она появляется в момент перемещения в катушке индуктивности магнита постоянной природы. Результатом такого движения является появление тока, с одновременным увеличением магнитного потока. Поскольку обмотка у катушки металлическая, а структура металла – кристаллическая решётка, то можно объяснить физические свойства этого явления.

Электроны, находящиеся в этой решётке, при отсутствии магнитного воздействия находятся в покое. Движения никакого нет. Оно начинается в тот момент, когда электроны попадают под воздействие переменного МП (поле изменяется при перемещении постоянного магнита).

Значение возникающего в катушке тока зависит от диаметра жилы и количества витков, физических характеристик магнита и скорости его движения.

Единица размерности в системе Си рассматриваемой характеристики – тесла. Она обозначается буквами Тл.

Важно! Электроны в решётке, после попадания катушки в МП, разворачиваются под некоторым углом и выстраиваются вдоль силовых линий МП. Количество ориентированных частиц и однородность их размещения зависимы от величины поля.

Вектор – это вектор индукции магнитного поля (градиентный параметр МП).

Явление электромагнитной индукции

Электромагнитная индукция – явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.

Явление электромагнитной индукции было открыто М. Фарадеем.

Опыты Фарадея

• На одну непроводящую основу были намотаны две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй – подключены к источнику тока. При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
• Первая катушка была подключена к источнику тока, вторая, подключенная к гальванометру, перемещалась относительно нее. При приближении или удалении катушки фиксировался ток.
• Катушка замкнута на гальванометр, а магнит движется – вдвигается (выдвигается) – относительно катушки.

Опыты показали, что индукционный ток возникает только при изменении линий магнитной индукции. Направление тока будет различно при увеличении числа линий и при их уменьшении.

Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.

Объяснения возникновения индукционного тока

Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС. Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.

Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 году.

Свойства вихревого электрического поля:

• источник – переменное магнитное поле;
• обнаруживается по действию на заряд;
• не является потенциальным;
• линии поля замкнутые.

Будет интересно➡ NPN транзистор

Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике.

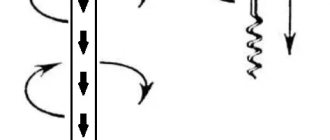
Направление вектора МИ

Направление магнитных полей может указать стрелка магнита, помещаемая в эти поля. Она будет крутиться до тех пор, пока не остановится. Северный конец стрелки покажет, куда ориентирован B→ орт того или иного поля.

Линии магнитной индукции

Таким же образом ведёт себя рамка с током, имеющая возможность без помех ориентироваться в МП. Направленность вектора индукции указывает ориентацию нормали к такому замкнутому электромагнитному контуру.

Внимание! Здесь используют правило буравчика (правого винта). Если винт вращать так, как направлен ток в рамке, то поступательное продвижение винта совпадёт с направлением положительной нормали.

В некоторых случаях, чтобы найти направление, применяют правило правой руки.

Наглядное отображение линий МИ

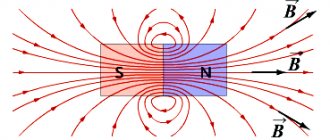
Линию, к которой можно провести касательную, совпадающую с B→, называют линией магнитной индукции (МИ). С помощью таких линий можно визуально отобразить магнитное поле. Это сомкнутые контурные чёрточки, которые охватывают токи. Их густота всегда пропорциональна величине B→ в конкретной точке МП.

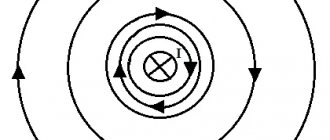
Информация. Когда имеют дело с МП прямого движения заряженных частиц, то эти линии изображаются в виде концентрических окружностей. Они имеют свой центр, расположенный на прямой линии с током, и находятся в плоскостях, расположенных под прямым углом к нему.

С направлением магнитных линий также можно определиться, пользуясь правилом буравчика.

Материал сердечников трансформатора

Нередко считается, что импульсные трансформаторы нужно выполнять на ферритах. Это верно лишь отчасти. Многие импульсные устройства работают на довольно низких частотах. Если частота меньше 3 кГц, то однозначно оправданным выбором будет трансформаторное железо. На частотах 3 — 7 кГц выбор не очевиден. Для частот выше 7 кГц потребуются ферриты. Сейчас появились сердечники из порошкового железа. Они сочетают в себе преимущества феррита и трансформаторного железа и хорошо показывают себя на частотах до 100 кГц. Однако они пока малодоступны.

Вашему вниманию подборки материалов:

Конструирование источников питания и преобразователей напряжения Разработка источников питания и преобразователей напряжения. Типовые схемы. Примеры готовых устройств. Онлайн расчет. Возможность авторам

Практика проектирования электронных схем Искусство разработки устройств. Элементная база. Типовые схемы. Примеры готовых устройств. Подробные описания. Онлайн расчет. Возможность задать вопрос авторам

Модуль вектора магнитной индукции

Закон электромагнитной индукции — формула

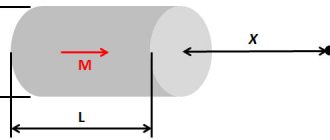
Чтобы определить величину вектора МИ, нужно узнать его модуль. Как определяется модуль вектора магнитной индукции (градиент)? Это можно понять на примере небольшой модели. Если поместить в поле подковообразного магнита горизонтально подвешенный проводник, то МП магнита будет действовать только на участок, расположенный в междуполюсном промежутке. Сила F→, действующая на этот участок, будет направлена под прямым углом к линиям индукции и самому проводнику. Она достигает своего максимума, когда орт МИ располагается перпендикулярно проводнику.

Значение модуля B→ будет равно отношению максимального значения этой силы F→ к произведению длины отрезка ∆L на силу движения зарядов (I), а именно:

B = Fm/I*∆L.

Единицы измерения магнитных величин.

Система единиц (СИ) определяет единицы магнитных величин на осно­вании законов электромагнетизма через соответствующие электрические и ме­ханические единицы.

Максимальная напряженность

имеет место на внешней поверхности проводника. Внутри проводника также возникает магнитное поле, но напря­женность его уменьшается по направлению от внешней поверхности к его оси. Напряженность магнитного поля Н измеряется в амперах на метр (А/м).

1 А/м -это .напряженность магнитного поля, возбуждаемого током 12,566 А прямого, бесконечно длинного проводника на расстоянии 2 м от его оси. Размерность единицы (А/м) и определение ее даны на основании закона полного тока.

Магнитный поток

Ф измеряется в веберах (Вб). 1 Вб равен такой маг­нитный поток, при убывании которого до нуля за 1 с в контуре, сцепленном с этим магнитным потоком, возникает ЭДС индукции, равная 1 В: Вб = В • с.

Магнитная индукция В

измеряется в теслах (Тл). 1 Тл — это индукция такого равномерного магнитного поля, в котором магнитный поток через пло­щадь в 1 м2, перпендикулярную направлению магнитного поля, равен одному 1Вб:Тл = Вб/м2.

Абсолютная магнитная проницаемость и магнитная постоянная

измеряются в . Так как следовательно, единица абсолютной магнитной проницаемости должна измеряться в

Индуктивность измеряется в генри (Гн). Индуктивностью в1Гн обладает такой контур, в котором ток, силой 1 А создает сцепленный с контуром магнитный поток в 1 Вб. Так как Гн = , то единица будет Гн/м.

Наряду с системами СИ допускается применение магнитных единиц не-рационализированной электромагнитной системы СГС, основными единицами которой являются сантиметр, грамм, секунда. Формулы электромагнетизма в этой системе нерационализированные; они содержат коэффициент .

В этой системе напряженность Н

измеряется в эрстедах (Э):

Магнитный поток Ф измеряется в максвеллах (Мкс). 1 Вб = 108Мкс.

Магнитная индукция В измеряется в гауссах (Гс). 1 Тл = 104Гс,

Индуктивность измеряется в сантиметрах (см). 1 Гн = 109см.

Закон полного тока

определяет зависимость напряженности магнитного поля от токов, его возбуждающих. В простейшем случае напряженность Н маг­нитного поля прямолинейного длинного провода на расстоянии х от его оси составит:

Здесь представляет собой длину окружности, описанной вокруг провода радиусом х.

Во всех точках этой окружности вследствие симметрии системы напряженность магнитного поля одинакова, а сама окружность совпа­дает с магнитной линией, описанной вокруг проводника

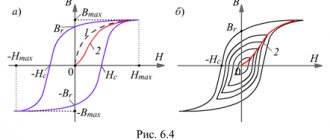
Устройство магнитной системы и принцип ее расчета

Магнитный поток в ЭМ возникает из-за наличия тока в обмотках: в ма­шинах постоянного тока и синхронных по обмоткам возбуждения проходит по­стоянный ток, по обмоткам якоря — переменный; в асинхронных машинах и трансформаторах по всем обмоткам проходит переменный ток.

На (рис. ) показана в схематическом виде часть четырехполюсной ма­шины постоянного тока и изображена картина магнитного потока, создаваемо­го основными полюсами (добавочные полюсы не показаны, чтобы не загромо­ждать чертеж). Ввиду полной симметрии машины поток, создаваемый каждым из полюсов, делится относительно продольной осевой линии полюса на две части, образующие два одинаковых магнитных контура, расположенных сим­метрично по обе стороны от осевой линии данного полюса. Число таких конту­ров равно числу полюсов 2р машины, но при расчете намагничивающей силы достаточно иметь в виду только какой-нибудь один из них.

Для улучшения магнитной связи между обмотками и увеличения магнит­ного потока магнитная система машин выполняется из ферромагнитных мате­риалов, обладающих хорошей магнитной проводимостью. В большинстве слу­чаев применяется электротехническая сталь, легированная кремнием (1 —5,0 %) а

другими присадками, уменьшающими потери в переменном магнитном поле.

Основной поток Фо составляет только часть магнитного поля, создавае­мого полюсом. Другая часть магнитного поля, называемая потоком рассеяния Фа, ответвляется в пространство между полюсами и, следовательно, не прохо­дит в якорь и не участвует в создании ЭДС (рис. 3).

Цель расчета магнитной системы — установление связи между магнитным потоком Фо и токами в обмотках ЭМ.

Весь путь магнитного потока в электрической машине постоянного тока состоит из пяти участков (см. рис. 3): воздушного зазора длиной 25,, зубцово-го слоя длиной 2hz,

сердечника якоря длиной La , сердечника полюсов длиной 2hn, станины длиной £с.

Так как магнитный поток в поперечном разрезе машины распределяется симметрично относительно продольных осей полюсов, то расчет магнитной це­пи производят для 1/2р части машины (см. рис. 3).

По закону магнитной цепи:

(8)

где — магнитное сопротивление цепи

Здесь Lk —

длина участка магнитной цепи, Sk — площадь сечения участка магнитной цепи, µк — магнитная проницаемость участка магнитной цепи.

Отсюда, намагничивающая сила (н. с.) обмотки возбуждения

(9)

где: — намагничивающая сила вдоль магнитной цепи;

— магнитный поток элементарной трубки;

— элемент длинны трубки;

— магнитная проницаемость тел и сред, образующих данный участок цепи;

— сечение элементарной трубки.

При расчете основной н. с. машины Fo

мы делим магнитную цепь машины на участки с таким расчетом, чтобы в пределах каждого из этих участков можно было считать, что магнитный поток трубки, проницаемость и сечение ее остаются постоянными по всей длине трубки. В этих условиях мы рассматриваем магнитный поток каждого участка как состоящий из некоторого числа одинаковых элементарных трубок, имеющих длину l каждая, и равномерно распределенных по площади поперечного сечения S данного участка. Характерные для каждого участка магнитной цепи величины приводятся в табл.1.

Следует учесть, что длина элементарных трубок (магнитных линий) на участках в ярме и в спинке якоря неодинакова, поэтому расчет н. с. этих участ­ков ведут по длине средней магнитной линии (см. рис.).

Тогда основная н. с. машины, рассчитанная на пару полюсов, может быть записана в виде:

(10)

Так как согласно условию, магнитный поток распределяется по сечению каждого участка равномерно, то

(11)

В этих условиях уравнение (1) переписывается в следующем виде:

(12)

Уравнение (12) показывает, что для определения н. с. XFo нужно для каждого из пяти участков найти соответствующую ему напряженность магнит­ного поля Нг

и умножить ее на длину пути потока на этом участке. Так как , то напряженность магнитного поля данного участка зависит от величины магнитной индукции и магнитной проницаемости материала участка. Если магнитный поток и геометрические размеры всех участков заданы, то тем самым определяется магнитная индукция участка по формуле (2.12). Магнитная проницаемость участка зависит от магнитных свойств материала этого участка. Дпя немагнитных материалов, в частности, для воздушного зазора, имеем: µ0 = 4π 10-7 Гн/м в рационализированных системах МКСА и СИ; µ0 = 4π в рационализированной системе СГС. На практике при расчетах магнитных цепей электрических машин пользуются смешанной системой, в основу которой по­ложена система СГСМ с переводом единиц напряжения, тока, мощности и т. д. в практические единицы — вольт, ампер, ватт и т. д. В этом случае ц0 = 4π 10-1.

Зная индукцию для данного материала, можно определить напряженность магнитного поля Н

и построить кривую намагничивания В = f(H) этого материала.

Основные формулы для вычисления вектора МИ

Вектор магнитной индукции, формула которого B = Fm/I*∆L, можно находить, применяя другие математические вычисления.

Закон Био-Савара-Лапласа

Формула ЭДС индукции

Описывает правила нахождения B→ магнитного поля, которое создаёт постоянный электроток. Это экспериментально установленная закономерность. Био и Савар в 1820 году выявили её на практике, Лапласу удалось сформулировать. Этот закон является основополагающим в магнитостатике. При практическом опыте рассматривался неподвижный провод с малым сечением, через который пропускали электроток. Для изучения выбирался малый участок провода, который характеризовался вектором dl. Его модуль соответствовал длине рассматриваемого участка, а направление совпадало с направлением тока.

Интересно. Лаплас Пьер Симон предложил считать током даже движение одного электрона и на этом утверждении, с помощью данного закона, доказал возможность определения МП продвигающегося точечного заряда.

Согласно этому физическому правилу, каждый сегмент dl проводника, по которому протекает электрический ток I, образовывает в пространстве вокруг себя на промежутке r и под углом α магнитное поле dB:

dB = µ0 *I*dl*sin α /4*π*r2,

где:

• dB – магнитная индукция, Тл;
• µ0 = 4 π*10-7 – магнитная постоянная, Гн/м;
• I – сила тока, А;
• dl – отрезок проводника, м;
• r – расстояние до точки нахождения магнитной индукции, м;
• α – угол, образованный r и вектором dl.

Важно! Согласно закону Био-Савара-Лапласа, суммируя векторы магнитных полей отдельных секторов, можно определить МП нужного тока. Оно будет равно векторной сумме.

Существуют формулы, описывающие этот закон для отдельных случаев МП:

• поля прямого перемещения электронов;
• поля кругового движения заряженных частиц.

Формула для МП первого типа имеет вид:

В = µ* µ0*2*I/4*π*r.

Для кругового движения она выглядит так:

В = µ*µ0*I/4*π*r.

В этих формулах µ – это магнитная проницаемость среды (относительная).

Рассматриваемый закон вытекает из уравнений Максвелла. Максвелл вывел два уравнения для МП, случай, где электрическое поле постоянно, как раз рассматривают Био и Савар.

Принцип суперпозиции

Для МП существует принцип, согласно которому общий вектор магнитной индукции в определённой точке равен векторной сумме всех векторов МИ, созданных разными токами в данной точке:

B→= B1→+ B2→+ B3→… + Bn→

Теорема о циркуляции

Изначально в 1826 году Андре Ампер сформулировал данную теорему. Он разобрал случай с постоянными электрическими полями, его теорема применима к магнитостатике. Теорема гласит: циркуляция МП постоянного электричества по любому контуру соразмерна сумме сил всех токов, которые пронизывают этот контур.

Стоит знать! Тридцать пять лет спустя Д. Максвелл обобщил это утверждение, проведя параллели с гидродинамикой.

Другое название теоремы – закон Ампера, описывающий циркуляцию МП.

Математически теорема записывается следующим образом.

где:

• B→– вектор магнитной индукции;
• j→ – плотность движения электронов.

Это интегральная форма записи теоремы. Здесь в левой части интегрируют по некоторому замкнутому контуру, в правой части – по натянутой поверхности на полученный контур.

Магнитный поток

Одна из физических величин, характеризующих уровень МП, пересекающего любую поверхность, – магнитный поток. Обозначается буквой φ и имеет единицу измерения вебер (Вб). Эта единица характерна для системы СИ. В СГС магнитный поток измеряется в максвеллах (Мкс):

108 Мкс = 1 Вб.

Магнитный поток φ определяет величину МП, пронизывающую определённую поверхность. Поток φ зависит от угла, под которым поле пронизывает поверхность, и силы поля.

Формула для расчёта имеет вид:

φ = |B*S| = B*S*cosα,

где:

• В – скалярная величина градиента магнитной индукции;
• S – площадь пересекаемой поверхности;
• α – угол, образованный потоком Ф и перпендикуляром к поверхности (нормалью).

Внимание! Поток Ф будет наибольшим, когда B→ совпадёт с нормалью по направлению (угол α = 00). Аналогично Ф = 0, когда он проходит параллельно нормали (угол α = 900).

Вектор магнитной индукции, или магнитная индукция, указывает направление поля. Применяя простые методы: правило буравчика, свободно ориентирующуюся магнитную стрелку или контур с током в магнитном поле, можно определить направление действия этого поля.

Магнитное поле: все формулы

В однородное поле помещают плоские контуры – изготовленные из точнейшей проволоки замкнутые проводники – с током. Измерения пикового вращающего момента показывает, что он:

1. прямо пропорционален силе протекающего через контур электрического тока I;
2. зависит от площади контура S;
3. не зависит от формы замкнутого проводника при равной площади.

Магнитный момент контура с током равен:

pm = IS.

Рассмотрим остальные формулы, позволяющие рассчитать электромагнитное поле.

Вращающий и магнитный моменты характеризуют электромагнитную индукцию, по модулю она равняется:

B= Mmax : pm.

Измеряется в теслах (Тл), названа в честь величайшего сербского учёного XX века Николы Теслы.

При расчётах неоднородных полей в них помещают маленькие контуры, по габаритам сравнимые с расстояниями, на которых наблюдаются изменения.

Магнитное полевое образование характеризуется напряжённостью H, пропорциональной индукции в вакууме:

B = μ0H,

μ0 = 4π*10-7 Гн/м или Тл*м/А.

При вычислениях для вещества добавляется коэффициент магнитной проницаемости μ, для вакуума он равен единице.

B = μ μ0H.

Магнитная индукция соленоида:

B = μ0nI, здесь:

• n = N : l, N – число витков катушки, l – её длина;
• I – сила протекающего тока.

Формула энергии W магнитного поля для соленоида:

W = LI2 : 2 = ФI : 2

• L – индуктивность катушки;
• I – сила тока;
• Ф – магнитный поток.

Сила взаимодействия между проводниками с электрическим током:

F = μ μ0I1I2l : 2πr, здесь:

• I1, I2 – сила тока в обоих проводниках;
• l – их длина;
• r – расстояние между проводами с током.

Наибольший момент:

Mmax= BIS;

S – площадь контура.

Электромагнитное поле образуется вокруг намагниченных тел и проводников с током.

Поделитесь в социальных сетях: 18 октября 2022, 18:15 Физика 0.00% 00