Закон полного тока для магнитного поля: физический смысл, формулы

В электрических цепях всегда присутствует магнитное поле, которое оказывает электромагнитное взаимодействие с токами этих цепей. Данный фактор учитывается при расчетах цепей, а закон полного тока для магнитного поля является инструментом для подобных вычислений.

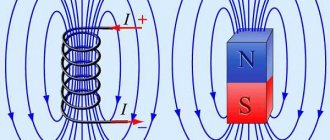
Если поднести магнитную стрелку к проводнику, по которому течёт ток, её положение изменится. Это говорит о наличии вокруг проводника кроме электрического ещё и магнитного поля. В результате многочисленных исследований электромагнитных явлений установлено, что существует взаимное влияние полей, имеющих электрическую и магнитную природу.

Физический смысл закона

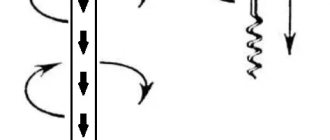
Рассмотрим упрощённый вариант влияния магнитной индукции на электрическое поле. Для этого представим себе два параллельных проводника, по которым циркулируют постоянные токи, например, I1 и I2. Вблизи этих проводников образуется поле, которое мысленно можно ограничить неким контуром L – воображаемой замкнутой фигурой, плоскость которой пересекает потоки движущихся зарядов.

В пределах плоскости, охватываемой контуром L, формируется магнитное поле, напряжённость которого распределена в соответствии с направлениями токов. При этом циркуляция вектора магнитного поля в плоскости замкнутого контура прямо пропорциональна сумме токов, пронзающих данный контур. Полный электрический ток равен векторной сумме его составляющих:

Направления векторов I1 и I2 определяется по правилу буравчика.

Приведённые выше рассуждения можно рассматривать в качестве примера изображающего упрощённую модель частного случая рассматриваемого закона. В действительности же, процессы взаимного влияния магнитных и электрических полей намного сложнее, и они описываются интегральными и дифференциальными уравнениями Максвелла.

Токи смещения. Теорема о циркуляции магнитного поля переменных токов.

Ток смещения или абсорбционный ток — величина, прямо пропорциональная скорости изменения электрической индукции.

Если переменное магнитное поле создает поле электрическое, то разумно предположить существование и обратного процесса: изменяющееся электрическое поле порождает поле магнитное. Такое явление действительно существует и носит не совсем обычное название ток смещения

По Максвеллу ток проводимости

замыкается в конденсаторе
током смещения
Точная формулировка

В вакууме, а также в любом веществе, в котором можно пренебречь поляризацией либо скоростью её изменения, током смещения (с точностью до универсального постоянного коэффициента) называется[3] поток вектора быстроты изменения электрического поля через некоторую поверхность[4] :

(СИ)

(СГС)

В диэлектриках (и во всех веществах, где нельзя пренебречь изменением поляризации) используется следующее определение:

(СИ)

(СГС),

где D — вектор электрической индукции (исторически вектор D назывался электрическим смещением, отсюда и название «ток смещения»)

Соответственно, плотностью тока смещения в вакууме называется величина

(СИ)

(СГС)

а в диэлектриках — величина

(СИ)

(СГС)

Теорема о циркуляции магнитного поля

Циркуляция магнитного поля постоянных токов по всякому замкнутому контуру пропорциональна сумме сил токов, пронизывающих контур циркуляции.

Теорема о циркуляции утверждает, что циркуляция вектора В магнитного поля постоянных токов по любому контуру L всегда равна произведению магнитной постоянной μ0на сумму всех токов, пронизывающих контур:

Циркуляцией вектора магнитной индукции В по заданному контуру называется интеграл

Система уравнений Максвелла.

Уравне́ния Ма́ксвелла — система уравнений в дифференциальной или интегральной форме, описывающих электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и сплошных средах. Вместе с выражением для силы Лоренца, задающим меру воздействия электромагнитного поля на заряженные частицы, образуют полную систему уравнений классической электродинамики, называемую иногда уравнениями Максвелла — Лоренца.

Дифференциальная форма

Уравнения Максвелла представляют собой в векторной записи систему из четырёх уравнений, сводящуюся в компонентном представлении к восьми (два векторных уравнения содержат по три компоненты каждое плюс два скалярных) линейным дифференциальным уравнениям в частных производных первого порядка для 12 компонент четырёх векторных функций ( ):

Название	СГС	СИ	Примерное словесное выражение
Закон Гаусса	Электрический заряд является источником электрической индукции.
Закон Гаусса для магнитного поля	Не существует магнитных зарядов
Закон индукции Фарадея	Изменение магнитной индукции порождает вихревое электрическое поле.
Теорема о циркуляции магнитного поля	Электрический ток и изменение электрической индукции порождают вихревое магнитное поле

Жирным шрифтом в дальнейшем обозначаются векторные величины, курсивом — скалярные.

Введённые обозначения:

· — плотность стороннего электрического заряда (в единицах СИ — Кл/м³);

· — плотность электрического тока (плотность тока проводимости) (в единицах СИ — А/м²); в простейшем случае — случае тока, порождаемого одним типом носителей заряда, она выражается просто как , где — (средняя) скорость движения этих носителей в окрестности данной точки, — плотность заряда этого типа носителей (она в общем случае не совпадает с )[29]; в общем случае это выражение надо усреднить по разным типам носителей;

· — скорость света в вакууме (299 792 458 м/с);

· — напряжённость электрического поля (в единицах СИ — В/м);

· — напряжённость магнитного поля (в единицах СИ — А/м);

· — электрическая индукция (в единицах СИ — Кл/м²);

· — магнитная индукция (в единицах СИ — Тл = Вб/м² = кг•с−2•А−1);

· — дифференциальный оператор набла, при этом:

означает ротор вектора,

означает дивергенцию вектора.

Интегральная форма

При помощи формулы Остроградского — Гаусса и теоремы Стокса дифференциальным уравнениям Максвелла можно придать форму интегральных уравнений:

Название	СГС	СИ	Примерное словесное выражение
Закон Гаусса	Поток электрической индукции через замкнутую поверхность пропорционален величине свободного заряда, находящегося в объёме , который окружает поверхность .
Закон Гаусса для магнитного поля	Поток магнитной индукции через замкнутую поверхность равен нулю (магнитные заряды не существуют).
Закон индукции Фарадея	Изменение потока магнитной индукции, проходящего через незамкнутую поверхность , взятое с обратным знаком, пропорционально циркуляции электрического поля на замкнутом контуре , который является границей поверхности .
Теорема о циркуляции магнитного поля	Полный электрический ток свободных зарядов и изменение потока электрической индукции через незамкнутую поверхность пропорциональны циркуляции магнитного поля на замкнутом контуре , который является границей поверхности .

Введённые обозначения:

· — двумерная замкнутая в случае теоремы Гаусса поверхность, ограничивающая объём , и открытая поверхность в случае законов Фарадея и Ампера — Максвелла (её границей является замкнутый контур ).

· — электрический заряд, заключённый в объёме , ограниченном поверхностью (в единицах СИ — Кл);

· — электрический ток, проходящий через поверхность (в единицах СИ — А).

При интегрировании по замкнутой поверхности вектор элемента площади направлен из объёма наружу. Ориентация при интегрировании по незамкнутой поверхности определяется направлением правого винта, «вкручивающегося» при повороте в направлении обхода контурного интеграла по .

Упрощенный подход

Выразить закон в дифференциальном представлении довольно сложно. Потребуется вводить дополнительные компоненты. Необходимо учитывать влияние молекулярных токов. Наличие вихревых токов является причиной образования магнитного вихревого поля в пределах контура.

Вектор электрического смещения сравним с вектором напряжённости присутствующего магнитного поля H. При этом Ориентация вектора смещения зависит от быстроты изменения магнитной индукции.

Для упрощения вычислений на практике часто пользуются формулами закона для магнитного поля полных токов, представленных в виде суммирования предельно малых участков контура, с учётом влияния вихревых полей. При реализации этого метода контур мысленно разбивают на бесконечно малые отрезки. На этих отрезках проводники считаются прямолинейными, а магнитное поле на таких участках контура считают однородным.

На одном дискретном участке вектор напряженности Um определяется по формуле: Um= HL×ΔL, где HL– циркуляция вектора напряжённости на участке ΔL контура L. Тогда суммарная напряжённость UL вдоль всего контура вычисляется по формуле: UL= Σ HL× ΔL.

Циркуляция векторного поля. Формула Стокса

Карта сайта

Заключительный урок по основам векторного анализа будет посвящён ещё одной характеристике векторного поля под названием циркуляция. С чем у нас ассоциируется этот термин на обывательском уровне? Циркуляция воздуха, циркуляция жидкости в некоторой системе; причём латинский корень данного слова (circulare) говорит нам, о том, что процесс идёт «по кругу».

Всё верно, понятие циркуляции пришло в теорию поля из гидродинамической задачи, где нужно было оценить движение жидкости по замкнутому контуру. Построим простейшую модель: пусть в некой замкнутой трубе циркулирует жидкость, и её движение описывается полем скоростей . Рассмотрим произвольную замкнутую линию тока . Упрощённо будем полагать, что каждой точке линии соответствует торчащий из неё вектор поля, который показывает направление и скорость движения жидкости в данной точке.

Циркуляция () векторного поля по контуру – это скалярная величина, численно равная криволинейному интегралу 2-го рода по этому контуру:

Согласно общему принципу интегрирования, данный интеграл объёдиняет проекции «торчащих» из контура векторов на координатные оси по всем бесконечно малым кусочкам контура, что и является оценкой движения жидкости. И непосредственно из интеграла видно, что циркуляция зависит от двух вещей:

– длины самого контура (чем длиннее, тем больше циркуляция);

– скорости течения * (чем длиннее векторы «эф», тем больше их бесконечно малые проекции и тем больше значение ).

* Со временем понятие циркуляции распространилось на произвольное векторное поле, где циркулировать в прямом смысле нечему

При этом контур, очевидно, можно обойти двумя способами: в одном направлении или в противоположном. В обоих случаях получится одно и то же абсолютное значение циркуляции с разными знаками (если, конечно, ). На практике чаще используется обход против часовой стрелки – когда для «идущего по контуру» человека ограниченная контуром область остаётся по левую руку. Такое направление обхода называют положительным.

Следует также заметить, что требование замкнутости контура не является обязательным – циркуляцию можно вычислить и по произвольной кусочно-гладкой линии, которая позволяет беспроблемно интегрировать. Однако исторически и методически сложилось так, что в практических задачах контур, как правило, замкнут.

И, если расписать криволинейный интеграл циркуляции для векторного поля подробно, то перед нами «откроется» её физический смысл:

А именно, циркуляция равна работе векторного поля по замкнутому контуру , о которой я, в том числе упоминал на первом уроке по теории поля. Этот смысл больше характерен для силовых полей, но и в гидродинамической модели результат можно интерпретировать как работу поля скоростей по перемещению материальной точки.

Таким образом, сегодня у нас будет две задачи «в одном флаконе»! К тому же криволинейных интегралов по пространственным контурам мы почти не решали, и сейчас самое время наверстать упущенное:

Пример 1

Вычислить циркуляцию векторного поля вдоль треугольника в положительном направлении.

Решение: изобразим треугольник на чертеже и обязательно пометим стрелочками порядок его обхода:

Циркуляция векторного поля по замкнутому контуру равна криволинейному интегралу 2-го рода по данному контуру, и в силу свойства аддитивности:

Как говорится, разделяй и властвуй:

1) Вычислим циркуляцию по отрезку :

По точкам и найдём направляющий вектор прямой : , и поскольку его «зетовая» координата равна нулю, то канонические уравнениЯ прямой принимают следующий вид: . Мысленно проверяем, что координаты точек «а» и «бэ» удовлетворяют полученным уравнениям. Так как , то у нас есть возможность свести криволинейный интеграл к определённому интегралу с интегрированием по «икс» или по «игрек». Из левой пропорции выражаем: и находим дифференциал: – таким образом решение сведётся к переменной «икс», которая в соответствии с направлением интегрирования изменяется (смотрим на чертёж!) от 3 до 1:

Как вариант, из уравнений прямой можно выразить , найти и проинтегрировать по «игрек» от 0 до 2. Не упускаем отличную возможность проверки:

2) Вычислим циркуляцию векторного поля по отрезку :

Направляющий вектор соответствующей прямой найдём по точкам : – и поскольку все его координаты отличны от нуля, то нам не удастся «обнулить» какую-либо переменную в криволинейном интеграле. Что делать? Запишем параметрические уравнения прямой – по точке (удобнее взять начало пути) и направляющему вектору : Нетрудно видеть, что началу отрезка соответствует значение , а концу – значение . Осталось найти дифференциалы параметрических уравнений: и АККУРАТНО подставить весь скарб:

3) И, наконец, вычислим циркуляцию поля по отрезку :

Поскольку путь лежит в плоскости , то «игрековая» координата будет равна нулю, что позволяет нам свести решение к определённому интегралу по «икс» либо по «зет». Составим канонические уравнения прямой по точке и направляющему вектору : – не забываем мысленно проверить, что координаты точек удовлетворяют полученным уравнениям.

Из пропорции проще выразить , найти и проинтегрировать по «зет» (внимание!) от 2 до 0 – строго по направлению обхода:

Не позволяй душе лениться – теперь выразим , найдём и проинтегрируем по «икс» от 0 до 3: , что и требовалось проверить.

Кстати, и в первом, и в этом пункте можно использовать и параметрические уравнения – кому как удобнее.

Таким образом, циркуляция векторного поля по замкнутому контуру:

Ответ:

Скорее всего, вам не очень понятен этот результат с точки зрения гидродинамики, и чуть позже я объясню его смысл. Но прежде ответим на старый сакраментальный вопрос: а нельзя ли проще?

Формула Стокса

Циркуляция векторного поля по замкнутому контуру равна потоку его ротора через поверхность , натянутую на данный контур в направлении, которое соответствует направлению обхода контура:

а именно, если смотреть на поверхность из острия её нормальных векторов (вектора), то путь по контуру должен быть ВИДЕН НАМ, как осуществляемый ПРОТИВ часовой стрелки. Посмотрите на треугольник (чертёж выше) со стороны острия единичного нормального вектора . Обход контура осуществляется против часовой стрелки? Да*. Значит, это и есть нужный вектор нормали, и поэтому нам следует вычислить поверхностный интеграл по верхней стороне треугольника.

* Посмотрите на ситуацию и с другой стороны треугольника

По формуле Стокса:

, где – единичный вектор нормали верхней стороны треугольника.

Примечание: по сути, в правой части записан поверхностный интеграл 2-го рода – уже сведённый к поверхностному интегралу 1-го рода

Найдём роторную функцию поля . Чтобы не запутаться, выпишем компоненты поля, и возьмём частные производные в «роторном» порядке:

Таким образом: , следовательно, наше поле потенциально и:

Ну ещё бы – если вспомнить физический смысл циркуляции (работа векторного поля по контуру), и вспомнить о том, что работа по замкнутому контуру в потенциальном поле равна нулю, то всё встаёт на свои места.

Таким образом, циркуляция векторного поля равна нулю не только по треугольнику , но и вообще по любому замкнутому контуру пространства. Из чего становится понятен и гидродинамический смысл задачи: представьте, что треугольник находится внутри замкнутой трубы. Поскольку поле скоростей потенциально, то циркуляция будет равна нулю не только по данному треугольнику, но и по любой внутренней замкнутой линии. Это говорит нам о том, что движение жидкости в трубе разнонаправлено и скомпенсировано – сколько циркулирует в одном направлении – столько проциркулирует и в другом.

На самом деле формулой Стокса мы пользовались и раньше: если контур полностью лежит в плоскости , то получается её частный случай под названием формула Грина:

, где – замкнутая область, ограниченная контуром . И фактически сейчас мы прорешали пространственный аналог Примера 12 урока Криволинейные интегралы по замкнутому контуру.

Интересно отметить, что рассмотренное в задаче поле является не только потенциальным, но ещё и соленоидальным:

Такие поля (одновременно потенциальные и соленоидальные) называют гармоническими. И под этот термин мне всегда представляется полноводная широкая река с ровным течением, по которой величественно, без малейшего отклонения от прямого курса плывёт разный мусор целая флотилия ладей. И в этом действительно есть какая-то завораживающая гармония. Однако, то лишь ассоциация – самостоятельно придумайте «бурный» пример

В курсе векторного анализа существует целый раздел, посвящённый гармоническим полям, но сейчас мы возвращаемся к делам практическим, и для самостоятельного решения я предлагаю вам аналогичную задачу:

Пример 2

Вычислить циркуляцию векторного поля вдоль треугольника в положительном направлении двумя способами: а) непосредственно, б) по формуле Стокса.

Это более распространённый случай, где все отрезки лежат в координатных плоскостях, и поэтому здесь можно обойтись исключительно декартовыми координатами. Впрочем, параметрические уравнения тоже неплохой вариант, ибо буковка там всего одна =) – главное, правильно разобраться с пределами изменения параметра.

При использовании формулы Стокса не путаемся – в ней вычисляется поток НЕ САМОГО поля , а его ротора . И да, тут потребуется составить уравнение плоскости.

НЕ ЛЕНИМСЯ и обязательно решаем это задание! Оно, может быть, не слишком интересно с точки зрения содержания, но крайне полезно для отработки техники решения криволинейных интегралов. В конце урока можно ознакомиться с образцом решения и некоторыми рациональными приёмами вычислений, позволяющими минимизировать трудозатраты и уменьшить риск ошибок.

Помимо контура-треугольника, пожалуй, популярнее только окружность:

Пример 3

Вычислить циркуляцию векторного поля вдоль замкнутого контура непосредственно и по формуле Стокса

Решение: предложенные уравнения задают окружность, лежащую в плоскости , радиуса 2 с центром на оси . Причём, в условии ничего не сказано о порядке обхода контура, и мы, в принципе, можем выбрать любой из них. Пойдём «традиционным» путём:

1) Вычислим работу векторного поля непосредственно. С «иксом», «игреком», «зет» и их дифференциалами тут всё прозрачно: и осталось проконтролировать пределы изменения параметра: – если , то – белая точка контура (см. чертёж); – если , то – самая верхняя точка контура. Таким образом, при изменении окружность «прорисовывается» в противоположном направлении по отношению к нашему порядку обхода, и поэтому интеграл следует взять от до 0:

Используем тригонометрические формулы :

Ответ:

Отрицательный знак говорит нам о том, что циркуляция осуществляется (полностью или преимущественно) против выбранного нами порядка обхода, и если бы мы обошли окружность в противоположном направлении, то получилось бы

2) Вычислим циркуляцию по формуле Стокса:

Найдём роторную функцию:

Поскольку поверхность , натянутая на контур , представляет собой плоскую фигуру (круг), то для всех её точек единичный вектор нормали может «смотреть» лишь в две стороны. Какой вектор выбрать: или ? Вспоминаем правило: из острия вектора обход контура должен быть ВИДЕН НАМ против часовой стрелки. Этому условию удовлетворяет вектор . Обязательно взгляните на круг и с другой стороны – с этой точки зрения контур обходится ПО часовой стрелке, и поэтому вектор не годится.

Найдём скалярное произведение:

Теперь заряжаем формулу Стокса:

Здесь можно сослаться на то, что интеграл равен площади -круга: и сразу дать ответ , но мы пойдём академичным путём.

Коль скоро, поверхность «полноценно» проецируется лишь на плоскость , то ничего не остаётся, как применить частную формулу . Особо подчёркиваю, что это частный случай, и если бы под интегралом были хоть какие-то переменные, то потребовалась бы полная версия

Но у нас всё проще:

И здесь снова можно сослаться, что полученный двойной интеграл численно равен площади круга такого же радиуса, но я таки «добью» интеграл с помощью «экзотического» перехода к полярным координатам в плоскости . С порядком обхода тут всё ясно: – обратите внимание, что полярный угол изменяется в стандартном направлении, от полуоси в сторону полуоси . Грубо говоря, роль «игрека» здесь выполняет переменная «зет», а значит :

Ответ:

Если выбрать другое направление обхода окружности , то придётся использовать противоположно направленный вектор , из-за чего, очевидно, сменится знак. Однако отрицательный знак ничем не хуже положительного и говорит лишь о том, что мы подсчитали циркуляцию полностью или преимущественно «против течения».

Пара задач для самостоятельного решения. Попроще:

Пример 4

Вычислить циркуляцию векторного поля вдоль замкнутого контура непосредственно и по формуле Стокса. Выбрать положительное направление обхода.

В образце я привёл скрупулезное решение, но на практике можно пользоваться и геометрическим смыслом интегралов, обычно преподаватели к этому относятся лояльно.

И задачка позанятнее:

Пример 5

Найти модуль циркуляции векторного поля вдоль контура

Контур здесь представляет собой линию пересечения цилиндра и плоскости, а именно, эллипс; и, кстати, на уроке о тройных интегралах в Примере 7 я рассказывал, как построить такое сечение. Интересно отметить, что тут можно легко обойтись без чертежа, поскольку требуется найти абсолютное значение циркуляции, то направление обхода не имеет значения – просто тупо интегрируем по «тэ» от 0 до . С параметрическими уравнениями «косого» эллипса, думаю проблем возникнуть не должно. Но, это палка о двух концах – возможно, вам покажется проще решение вторым способом.

Существует и более сложные задачи, однако в рамках данного урока этого будет достаточно, ибо лучше проще – да понятнее. Кроме того, я далеко не всё рассказал по теме, в частности о том, что само понятие ротора определяется через циркуляцию и поверхность, натянутую на контур + ещё один интересный момент, который касается поверхности. Читайте, например, 3-й том Фихтенгольца.

Ну а я поздравляю вас с успешным прохождением занимательного курса по теории поля. Надеюсь, он был понятен, интересен и полезен, и теперь никому не будут страшнЫ, по крайне мере, навороченные обозначения в учебниках.

Всё что осталось сделать – это вручить вам в руки лопату и отправить на обширное поле векторного анализа =) Дополнительные задачи с решениями есть в соответствующем архиве банка решений, библиотеке mathprofi.com, или в этом решебнике. Только будьте осторожны и критичны – недочёты и ошибки могут быть где угодно.

Желаю успехов!

Решения и ответы:

Пример 2: Решение: изобразим контур интегрирования на чертеже: а) Решим задачу непосредственно:

1) Вычислим циркуляцию по отрезку . Так как , то: Составим уравнения прямой по точке и направляющему вектору : , откуда выразим: При этом изменяется от 0 до 3: Проверьте решение другим способом!

2) Вычислим циркуляцию поля по отрезку . Так как , то: Составим уравнения прямой по точке и направляющему вектору : , откуда: Найдём дифференциал: изменяется от 3 до 0: Самостоятельно проведите решение по переменной «зет»

3) Вычислим циркуляцию поля по отрезку . Так как , то: Составим уравнения прямой по точке и направляющему вектору : В данном случае выгоднее выразить изменяется от 3 до 0:

Таким образом, циркуляция по замкнутому контуру:

Ответ:

б) Вычислим циркуляцию векторного поля по формуле Стокса: Найдём ротор векторного поля: . В данном случае: Таким образом: Составим уравнение плоскости по точке и векторам : Запишем вектор нормали этой плоскости: и найдём соответствующий единичный вектор: Примечание: из острия данного вектора обход контур виден нам против часовой стрелки, следовательно, это и есть нужный вектор нормали Найдём скалярное произведение: Таким образом: Для вычисления поверхностного интеграла 1-го рода используем формулу , где – проекция треугольника на плоскость . В данном случае: Двойной интеграл численно равен площади треугольника :

Ответ:

Пример 4: Решение: выполним чертёж: 1) Вычислим работу векторного поля непосредственно: Таким образом:

2) Вычислим циркуляцию по формуле Стокса: , где – поверхность, натянутая на контур Найдём . В данном случае: Скалярное произведение: Таким образом: Спроецируем поверхность на плоскость и воспользуемся формулой , где – проекция поверхности . В данном случае : Перейдем к полярным координатам в плоскости :

Ответ:

Пример 5: Решение: запишем параметрические уравнения цилиндра: (любое действительное число) Подставим первые два уравнения в уравнение плоскости: Таким образом, сечение цилиндра плоскостью (эллипс) определяется уравнениями: Найдём дифференциалы: и вычислим циркуляцию векторного поля по контуру Г в направлении, которое соответствует изменению параметра в пределах :

Выполнять упрощения и считать интегралы, конечно же, удобнее по отдельности =)

Ответ:

Постарайтесь прийти к этому же результату, используя формулу Стокса.

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

Zaochnik.com – профессиональная помощь студентам

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

Закон в интегральном представлении

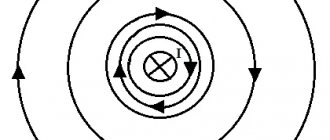
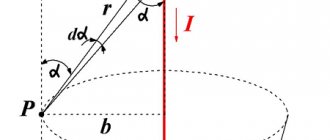
Рассмотрим бесконечно прямой проводник, по которому циркулирует электрический ток, образующий поле, ограниченное контуром в виде окружности. Плоскость, пронизывающая проводник, – это круг, очерчённый линией данной окружности (см. рис. 1).

Рис. 1. Поле бесконечно прямого тока

Воспользуемся методом разбиения контура на мизерные участки dl (элементарные векторы длины контура). Пусть φ – угол между векторами dl и B. В нашем случае, при суммировании отрезков, вектор индукции B поворачивается так, что он очерчивает круг, то есть угол φ → 2π.

Из теоремы Остроградского-Гаусса вытекает формула:

Учитывая, что cos φ = 1,

следовательно:

Данная формула – постулат, подтверждённый экспериментально. Согласно этому постулату, циркуляция вектора B по окружности, то есть по замкнутому контуру, равна μ0I, где μ0 = 1/c2 ε0 – магнитная постоянная.

Ориентация вектора dB определяется путём применения правила буравчика. Это направление всегда перпендикулярно вектору плотности. Если проводников будет несколько (например, N), тогда

Каждый ток, с учётом знака, необходимо учитывать такое количество раз, которое соответствует числу его охватов контуром.

Ток берётся со знаком «+», если он по направлению обхода образует правовинтовую систему. При этом, отрицательным считается ток противоположного направления.

Заметим, что формула справедлива только для вакуума. В обычных условиях необходимо учитывать проницаемость среды.

Если ток распределён в пространстве (произвольный ток), тогда

где S – натянутая на контур поверхность, j – объёмная плотность тока. С учётом последнего выражения, формулу полного тока в вакууме можно записать:

Рис. 2. Иллюстрация закона для вакуума

Отсюда вытекает:

Закон справедлив не только для бесконечно прямолинейного проводника, но и для контуров, произвольной конфигурации.
Циркуляция вектора магнитной индукции B сориентированного вдоль магнитных линий, всегда отлична от нуля.
Ненулевая циркуляция свидетельствует о том, что магнитное поле прямолинейного, бесконечно длинного проводника не потенциально. Такое поле называют вихревым, либо соленоидным.

Циркуляция и поток вектора магнитной индукции

Циркуляция и поток вектора магнитной индукции (как и любого вектора вообще) определяются так же, как и для вектора напряженности электрического поля.

Циркуляцией по отрезку прямой однородного поля

называется скалярное произведение: , где — угол между векторами и .

Рассмотрим участок произвольной направленной кривой. Разобьем этот участок на мелкие отрезки , направленные так же, как и сама кривая. Тогда, циркуляцией вектора по участку кривой называется криволинейный интеграл , который представляет собой предел суммы при делении кривой на бесконечно малые отрезки:

Малый участок кривой можно считать прямым отрезком, а поле в пределах этого участка — однородным, поэтому каждое слагаемое в сумме представляет собой циркуляцию вектора по отрезку .

Циркуляцию вектора по замкнутой

кривой будем обозначать как .

Магнитным потоком

вектора в однородном поле через плоскую поверхность площади называется величина

, (3.19)

где — единичный вектор нормали к поверхности, — угол между направлением вектора и направлением нормали к поверхности. В системе СИ единица измерения магнитного потока Вебер

(Вб).

Теперь рассмотрим участок произвольной поверхности . Потоком вектора через участок поверхности называется поверхностный интеграл, представляющий собой предел суммы при делении поверхности на куски бесконечно малых площадей:

. (3.19,а)

Малый участок поверхности можно считать плоским, а поле в пределах этого участка – однородным, поэтому каждое слагаемое в сумме представляет собой поток вектора через плоскую поверхность .

Поток вектора через замкнутую

поверхность будем обозначать как .

Сформулируем две теоремы о циркуляции и потоке вектора магнитной индукции.

Теорема о циркуляции вектора магнитной индукции

(для поля в вакууме). Циркуляция вектора магнитной индукции по произвольному замкнутому направленному контуру:

, (3.20)

где — алгебраическая сумма токов, пронизывающих произвольную поверхность, натянутую на контур, по которому вычисляется циркуляция. Направление обхода контура и направление нормали к натянутой на него поверхности связаны правилом буравчика. Если ток идет по направлению нормали, то его следует считать положительным, если наоборот – отрицательным.

Например, циркуляция вектора магнитной индукции по контуру , изображенному на рис. 3.14, равна .

Теорема о потоке вектора магнитной индукции.

Поток вектора магнитной индукции через произвольную замкнутую поверхность равен нулю:

. (3.21)

Теоремы о циркуляции и потоке вектора магнитной индукции полезно сравнить с соответствующими теоремами для вектора напряженности электрического поля. Вспомним теорему о потоке вектора напряженности электрического поля (теорема Гаусса, см. формулу 1.18):

Смысл этой теоремы в том, что источниками электрического поля являются электрические заряды. Они и создают поток вектора напряженности электрического поля. Силовые линии начинаются на зарядах и обрываются на них же. А смысл теоремы о потоке вектора магнитной индукции в том, что магнитных зарядов в природе не существует. Поэтому магнитные силовые линии нигде не начинаются и не заканчиваются, они замкнуты. Это и означает, что поток вектора магнитной индукции через любую замкнутую поверхность равен нулю (сколько линий войдет внутрь поверхности, столько и выйдет).

Циркуляция вектора напряженности электрического поля по любому замкнутому контуру равна нулю (уравнение 1.34):

Смысл этого уравнения в том, что электрическое поле, созданное любой системой зарядов, является полем потенциальным (подробнее см. п. 1.12). Электрическое поле, помимо напряженности — силовой характеристики, имеет еще и энергетическую характеристику – потенциал. Теорема о циркуляции для вектора магнитной индукции говорит о том, что источниками магнитного поля являются электрические токи (по сути, движущиеся электрические заряды), которые и создают циркуляцию вектора . Кроме того, поскольку циркуляция вектора магнитной индукции по замкнутому контуру может быть отлична от нуля, магнитное поле – поле непотенциальное. Поля с замкнутыми силовыми линиями называют вихревыми или соленоидальными. Таковым и является магнитное поле.

Приведем несколько примеров на применение теоремы о циркуляции для магнитного поля.

Пример 3.6. Определить магнитное поле, создаваемое прямым бесконечно длинным проводником с током .

Решение. В качестве произвольного замкнутого контура выберем окружность с радиусом , центр которой находится на оси провода (такой контур совпадет с одной из силовых линий – см. рис. 3.13, а). В данном случае скалярное произведение . Поскольку контур пронизывается всего одним током , по теореме о циркуляции для магнитного поля получаем:

Величина вектора одинакова во всех точках контура, следовательно, её, как постоянную, можно вынести за знак интеграла:

Интеграл представляет собой просто длину контура . Таким образом,

откуда находим величину магнитного поля на расстоянии от провода:

Последнее выражение в точности совпадает с результатом, полученным в примере 3.3 (см. формулу 3.14) из закона Био-Савара-Лапласа.

Отметим, что формулой 3.14 можно пользоваться и в случае проводника конечных размеров при расчете поля приблизительно напротив центральной части проводника в точках, отстоящих от него на расстояниях, гораздо меньших длины проводника.

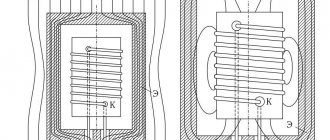
Пример 3.7. Найти магнитное поле внутри соленоида длиной , с числом витков и током .

Решение. В качестве контура обхода выберем прямоугольный контур АСDЕ

(см. рис. 3.15) так, что отрезок
АС
приблизительно лежит в средней части соленоида, а отрезок
DЕ
удален на большое расстояние от соленоида. По теореме о циркуляции для магнитного поля имеем:

Помещая небольшую магнитную стрелку в различные точки пространства, можно показать, что магнитное поле в средней части соленоида как снаружи, так и внутри, направлено параллельно оси соленоида. Следовательно, на отрезках контура СD

и
ЕA
скалярное произведение

а на отрезке АС

Таким образом, циркуляции магнитного поля по отрезкам CD

и
ЕA
равны нулю:

, ,

а по отрезку АС

(здесь величина вектора магнитной индукции вынесена за знак интеграла, поскольку она должна быть постоянна на отрезке АС

из-за осевой симметрии системы). На большом расстоянии от соленоида величина магнитной индукции близка к нулю, поэтому и циркуляция магнитного поля по отрезку
DЕ
равна нулю:

В итоге получим:

Сумма токов, пронизывающих контур ACDE

где — число витков, пронизывающих контур ACDE

(на рис. 3.15 эти витки показаны), — число витков, приходящееся на единицу длины соленоида. Тогда:

Если число витков на единицу длины соленоида представить как , где — общее число витков, а — длина соленоида, то:

Полученный результат совпадает с формулой (3.18) для поля на оси бесконечно длинного соленоида. Пользуясь теоремой о циркуляции, мы показали, что в случае достаточно длинного соленоида результат (3.18) можно использовать и для расчета поля в любой точке внутри соленоида в средней его части, а не только на оси.

Циркуляцией по отрезку прямой однородного поля

называется скалярное произведение: , где — угол между векторами и .

Циркуляцию вектора по замкнутой

кривой будем обозначать как .

Магнитным потоком

вектора в однородном поле через плоскую поверхность площади называется величина

, (3.19)

(Вб).

. (3.19,а)

Поток вектора через замкнутую

поверхность будем обозначать как .

Сформулируем две теоремы о циркуляции и потоке вектора магнитной индукции.

Теорема о циркуляции вектора магнитной индукции

, (3.20)

Например, циркуляция вектора магнитной индукции по контуру , изображенному на рис. 3.14, равна .

Теорема о потоке вектора магнитной индукции.

Поток вектора магнитной индукции через произвольную замкнутую поверхность равен нулю:

. (3.21)

Приведем несколько примеров на применение теоремы о циркуляции для магнитного поля.

Пример 3.6. Определить магнитное поле, создаваемое прямым бесконечно длинным проводником с током .

Интеграл представляет собой просто длину контура . Таким образом,

откуда находим величину магнитного поля на расстоянии от провода:

Пример 3.7. Найти магнитное поле внутри соленоида длиной , с числом витков и током .

Решение. В качестве контура обхода выберем прямоугольный контур АСDЕ

и
ЕA
скалярное произведение

а на отрезке АС

Таким образом, циркуляции магнитного поля по отрезкам CD

и
ЕA
равны нулю:

, ,

а по отрезку АС

В итоге получим:

Сумма токов, пронизывающих контур ACDE

где — число витков, пронизывающих контур ACDE

(на рис. 3.15 эти витки показаны), — число витков, приходящееся на единицу длины соленоида. Тогда:

Влияние среды

На результат взаимодействия магнитных потоков и постоянных токов влияет среда. Вещества обладают магнитной проницаемостью в потоке вектора индукции, что вносит коррективы на взаимодействие магнитной среды с токами проводимости. В однородной изотопной среде, где значение вектора электромагнитной индукции одинаково во всех точках, векторы B и H связаны между собой следующим соотношением:

где H — напряжённость магнитного поля, символом μ обозначена магнитная проницаемость.

Носители электрических зарядов создают собственные микротоки. Циркуляция вектора, характеризующего электростатическое поле, всегда нулевая. Поэтому электростатические поля, в отличие от магнитных, являются потенциальными.

Вектор B отображает результирующее значение полей макро- и микротоков. Линии электростатической индукции всегда остаются замкнутыми, в том числе и на положительных зарядах.

Рис. 3. Закон полного тока в веществе

Для полей, которые действуют в среде, состоящей из разных веществ, необходимо учитывать микротоки, характерные именно для конкретных структур, образующих данную среду.

Утверждение, изложенное выше, верно для полей соленоидов или любой другой структуры, обладающей свойствами конечной магнитной проницаемости.

Интегральная формула полного тока

Чтобы сформулировать закон, нужно представить замкнутый контур, внутри которого расположены один или несколько проводов, по которым проходит электроток. Контур может иметь произвольную форму, но он должен быть замкнутым. Чтобы произвести вычисления, необходимо разбить кривую на элементарные участки, которые настолько малы, что их с минимальной погрешностью можно считать прямыми отрезками.

В таком случае по правилу буравчика можно определить направление напряжённости магнитного поля, создаваемого каждым проводником на каждом элементарном отрезке. Чтобы получить суммарный результат, потребуется провести интегрирование по контуру.

Интегральная формула для закона полного тока выглядит следующим образом:

С учетом выражения

формулу можно записать так:

Она представляет собой постулат, подтвержденный экспериментально. Согласно ему циркуляция вектора магнитной индукции по замкнутому контуру равна μ0I, где μ0 — это магнитная постоянная.

Теорема о циркуляции вектора магнитной индукции основывается на законе Био-Савара и принципе суперпозиции магнитного поля. В общем виде она имеет такую формулировку:

Для произвольного тока (распределенного в пространстве) справедливо следующее равенство:

С учетом данного равенства формула полного тока в вакууме приобретает следующий вид:

В левой части применяется интегрирование по контуру вектора магнитной индукции. В правой части рассматривается сумма токов, проходящих внутри контура, умноженная на магнитную постоянную.

Взаимодействие электротоков и магнитных потоков зависит от той среды, в которой они пребывают. Кроме того, разные вещества обладают разной магнитной проницаемостью. С учетом этого закон полного тока для магнитного поля в веществе выражается такой формулой:

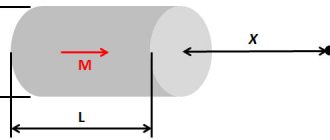
Торойд

В электротехнике часто приходится иметь дело с катушками разных видов и размеров. Катушка, образованная витками намотанными на сердечник тороидальной формы (в виде бублика), называется тороидом. Важными характеристиками сердечника тора являются его радиусы — внутренний (R1) и внешний (R2).

Поле внутри соленоида на расстоянии r от центра равно:

Выводы

На основании изложенного, приходим к заключению:

Закон полного тока устанавливает зависимость между напряжённостью магнитного поля и перемещением в этом поле электрических зарядов.
Действие закона распространяется на все среды, при допустимых плотностях тока.
Закон также выполняется в полях постоянных магнитов.

При вычислениях не имеет значения, какую формулу мы используем – суть закона остаётся неизменной: он выражает взаимодействия, которые происходят между токами и создаваемыми ими магнитными полями, пронизывающими замкнутый контур.

Выводы закона учитываются при конструировании электромагнитных устройств. Наличие завихрений в электромагнитных полях приводит к снижению КПД. Кроме того, вихревые поля негативно влияют на работоспособность электронных элементов, расположенных в зоне их действий.

Конструкторы электротехнических приборов стремятся свести к минимуму таких влияний. Например, вместо обычных соленоидов применяют тороидальные катушки, за пределами которых отсутствуют электромагнитные поля.

Решение задач по ТОЭ, ОТЦ, Высшей математике, Физике, Программированию…

Доказанная теоpема о циpкуляции относится к любому случаю магнитного поля пpи условии, если оно создано постоянными токами. Она выполняется и пpи наличии магнетика, в котоpом в пpисутствиии внешнего поля возникают связанные токи. В этом случае в пpавую часть уpавнения для циpкуляции вектоpа В должны войти как свободные, так и связанные токи. Рассмотpим такой случай. Пусть пpоводник с током помещен в магнетик (pис. 3.30). Магнетик может быть неодноpодным и иметь гpаницы (мы pассматpиваем общий случай). Какова циpкуляция вектоpа индукции магнитного поля по контуpу L? Она пpопоpциональна сумме токов, сцепленных с контуpом. Кpоме тока J нужно учесть связанные токи молекул магнетика. Молекулы мы уподобляем магнитным диполям. Только часть диполей-молекул нанизаны на контуp. Эти диполи как бы обpазуют некую тpубку, по повеpхности котоpой течет ток. Уpавнение для циpкуляции вектоpа В будет иметь вид:

(3.54)

Втоpой член спpава пpедставляет собой связанный ток, сцепленный с контуpом. Его можно пpедставить в виде некотоpого интегpала. Введем линейную плотность повеpхностного тока на тpубке (j’). Это сила тока, пpиходящегося на единицу длины тpубки. Тогда сила тока пpиходящегося на элемент длины тpубки d , будет pавна j’d . Ток же, текущий по повеpхности всей тpубки, опpеделяется интегpалом

Следовательно, уpавнение для циpкуляции пpимет вид:

(3.55)

Тепеpь можно воспользоваться фоpмулой (3.44), связывающей плотность тока на повеpхности тpубки с вектоpом намагниченности. Уpавнение для циpкуляции пеpепишется в виде

(3.56)

Несколько его пpеобpазуем:

(3.57)

Здесь учтено, что M сos a dl = Mdl, и что в общем случае с контуpом может быть сцеплен не один свободный ток. Вектоp

(3.58)

называется напpяженностью магнитного поля. Пpи введении такого понятия теоpема о циpкуляции сфоpмулиpуется в виде следующего соотношения:

(3.59)

Циpкуляция вектоpа напpяженности магнитного поля pавна сумме свободных токов, сцепленных с контуpом. Связанные токи, благодаpя введению понятия вектоpа напpяженности магнитного поля, не входят явно в уpавнение для циpкуляции. В этом и следует усматpивать смысл введения нового понятия -напpяженности магнитного поля. Оно вводится из чисто фоpмальных, pасчетных, сообpажений, из сообpажений удобства. Никакого физического смысла понятие напpяженности магнитного поля не имеет. Это видно из его опpеделения (3.58). Вектоp напpяженности поля по сути пpедставляет pазность двух вектоpов: индукции магнитного поля и намагниченности магнетика. Но эти два вектоpа хаpактеpизуют совеpшенно pазличные физические сущности: пеpвый является хаpактеpистикой поля, а втоpой характеpистикой вещества. Можно найти какие-нибудь фоpмальные истолкования для вектоpа Н, но они не могут пpидать какой-то физический смысл этой величине. Вектоp намагниченности М опpеделяется индукцией поля В в магнетике. В изотpопных паpа- и диамагнетиках этот вектоp пpопоpционален вектоpу В. Тогда из фоpмулы (3.58) следует, что для этих веществ вектоp М будет пpопоpционален и вектоpу Н. Именно эту зависимость М от Н (а не зависимость М от В) беpут на пpактике за основу, т.е. закон для вектоpа намагниченности записывают в следующем виде:

М = cН

(3.60)

(c > 0 у паpамагнетиков и c < 0 у диамагнетиков)

Коэффициент пpопоpциональности в этой фоpмуле называется магнитной воспpиимчивостью. Для паpа- и диамагнетиков он не зависит от Н, и имеет смысл его ввести как самостоятельное понятие. Тогда согласно фоpмуле (3.58) для вектоpа В получаем следующее выpажение:

(3.61)

Множитель 1+c=m называется магнитной пpоницаемостью, и полученное соотношение между В и Н пеpеписывается в виде

В = mm0Н (в СИ)

(3.62)

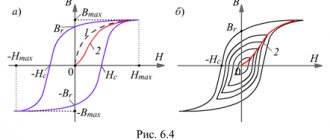
В паpа- и диамагнетиках есть величина постоянная, целиком хаpактеpизующая вещество, и этим, как и для , целиком опpавдано ее введение в физику. У феppомагнетиков опpеделяется не только свойствами вещества, но является и функцией поля, что накладывает на понятие магнитной пpоницаемости феppомагнетика элемент условности. Пpоиллюстpиpуем удобство введения понятия напpяженности магнитного поля на пpимеpе соленоида. Если соленоид имеет сеpдечник (напpимеp, железный), то фоpмула для индукции поля В имеет вид:

B = m(H)m0nJ

(3.63)

В этой фоpмуле зависимость (Н) может быть опpеделена (и не пpосто!) лишь эмпиpически. Но для вектоpа Н фоpмула имеет пpостой вид:

H = nJ

Напpяженность магнитного поля pавна пpоизведению числа витков, пpиходящихся на единицу длины соленоида, на силу тока. Таким обpазом, измеpение Н не составляет никакого тpуда. В заключение обpатим внимание на то, что в электpостатике нам пpишлось также ввести две хаpактеpистики поля: напpяженность и электpи-ческое смещение — Е и D. Соотношение между ними аналогично соотношению (3.62):

D = ee0E.

(3.64)

Но по своему смыслу фоpмулы (3.64) и (3.62) существенно отличаются: в электpостатике вектоp напpяженности имеет физический смысл, а вектоp электpического смещения является вспомогательной, искусственной величиной. В теоpии магнитного поля наобоpот: вектоp магнитной индукции имеет физический смысл, а напpяженность — искусственное понятие.