Расчет неразветвленной неоднородной магнитной цепи (обратная задача).

ТОЭ › Магнитные цепи

Магнитной цепью называется устройство, отдельные участки которого выполнены из ферромагнитных материалов, по которым замыкается магнитный поток. Примерами простейших цепей могут служить магнитопроводы кольцевой катушки и электромагнита, изображенного на рис. 6.11, а. Электрические машины и трансформаторы, электромагнитные аппараты и приборы имеют обычно магнитные цепи более сложной формы.

Если магнитная цепь выполнена из одного и того же материала и имеет по всей длине одинаковое сечение, то цепь называется однородной.

Если же отдельные участки цепи изготовлены из различных ферромагнитных материалов и имеют различные длины и сечения, то цепь — неоднородная.

Магнитные цепи, так же как и электрические, бывают разветвленные (рис. 6.11,6) и неразветвленные (рис. 6.11,а).

В неразветвленных цепях магнитный поток Ф во всех сечениях имеет одно и то же значение.

Разветвленные цепи могут быть симметричными и несимметричными. Цепь, представленная на рис. 6.11,6, считается симметричной, если правая и левая части ее имеют одинаковые размеры, выполнены из одного и того же материала и если МДС I1W1 и I2W2 одинаковы. При невыполнении хотя бы одного из указанных условий цепь будет несимметричной.

Разобьем неразветвленную магнитную цепь, например, на рис 6.11, а на ряд однородных участков, каждый из которых выполнен из определенного материала и имеет одинаковое поперечное сечение S вдоль всей своей длины. Длину каждого участка L будем считать равной длине средней магнитной линии в пределах этого участка. Из сказанного выше следует, что магнитные потоки всех участков неразветвленной цепи равны, т. е.

Ф1=Ф2=Ф3=…=Фn,

и поле на каждом участке можно считать однородным, т. е. Ф= BS; поэтому

B1S1=B2S2=B3S3=…=BnSn

Где n — число участков цепи. Магнитное напряжение на любом из участков магнитной цепи

Где H — Напряженность, (измеряется в ампер на метр А/М).

B — Магнитная индукция (измеряется в теслах Тл).

L — Длинна средне силовой линии проходящей через центр поперечного сечения магнитопровода.

S — площадь поперечного сечения магнитопровода.

— Магнитная постоянная.

μr — Магнитная проницаемость ферромагнетиков.

При заданном направлении тока в обмотке направление потока и МДС IW определяется по правилу буравчика.

9.1.1. Элементы магнитной цепи

Магнитной цепью (магнитопроводом) называется совокупность различных ферромагнитных и неферромагнитных частей электротехнических устройств для создания магнитных полей нужных конфигурации и интенсивности. В зависимости от принципа действия электротехнического устройства магнитное поле может возбуждаться либо постоянным магнитом, либо катушкой с током, расположенной в той или иной части магнитной цепи.

К простейшим магнитным цепям относится тороид из однородного ферромагнитного материала (рис. 9.1). Такие магнитопроводы применяются в многообмоточных трансформаторах, магнитных усилителях, в элементах ЭВМ и других электротехнических устройствах.

На рис. 9.2 показана более сложная магнитная цепь электромеханического устройства, подвижная часть которого втягивается в электромагнит при постоянном (или переменном) токе в катушке. Сила притяжения зависит от положения подвижной части магнитопровода.

На рис. 9.3 изображена магнитная цепь, в которой магнитное поле возбуждается постоянным магнитом. Если подвижная катушка, расположенная на ферромагнитном цилиндре, включена в цепь постоянного тока, то на нее действует вращающий момент. Поворот катушки с током практически не влияет на магнитное поле магнитной цепи. Такая магнитная цепь есть, например, в измерительных приборах магнитоэлектрической системы.

Рассмотренные магнитные цепи, как и другие возможные конструкции, можно разделить на неразветвленные магнитные цепи (рис. 9.1 и 9.3), в которых магнитный поток в любом сечении цепи одинаков, и разветвленные магнитные цепи (рис. 9.2), в которых магнитные потоки в различных сечениях цепи различны. В общем случае разветвленные магнитные цепи могут быть сложной конфигурации, например в электрических двигателях, генераторах и других устройствах.

В большинстве случаев магнитную цепь следует считать нелинейной, и лишь при определенных допущениях и определенных режимах работы магнитную цепь можно считать линейной.

Практическое применение

Часто формулу Ома используют для ответа на следующие вопросы:

• Вычисление магнитодвижущей силы.
• Вычисление количества витков провода, которое при заданном токе обеспечит нужную величину магнитного потока.

В качестве примера рассмотрим магнитную цепь, изображенную на рисунке ниже.

Условимся, что первый участок сделан из литой стали, второй — из электротехнической, третий — это воздушный зазор. Требуется определить количество витков обмотки, способной обеспечить магнитный поток, который равен 0.0036 Вебера для тока 2 Ампера. На основании указанных на схеме размеров можно вычислить длины участков и площади сечения детали:

Чтобы найти величину магнитной индукции, в соответствующую формулу следует подставить данные из условий задачи.

Чтобы найти величину напряжённости магнитного поля, потребуется в справочнике открыть график зависимости магнитной индукции и напряжённости и определить, какая величина соответствует значению 1.5 Тесла. Для литой стали эта величина приблизительно равна 700 А/м, а для электротехнической стали — 3000 А/м. Для воздушного разрыва искомое значение можно получить при использовании соответствующей формулы:

Используя закон Ома для магнитной цепи, можно определить количество витков, подставив найденные значения:

Следовательно, в рассматриваемом случае потребуется 4083.5 витков для обеспечения нужных параметров.

Как видим, при решении практических задач в электротехнике удобно пользоваться такими понятиями, как магнитодвижущая сила и магнитное сопротивление.

Следует также сказать, что без магнитных потоков не было бы, наверное, и такой отрасли, как электротехника. Ведь на свойствах магнитного поля основывается работа многих современных устройств, среди которых трансформаторы, электрические двигатели, генераторы, измерительные приборы, разные датчики.

9.1.2. Закон полного тока для магнитной цепи

Закон полного тока получен на основании многочисленных опытов. Этот закон устанавливает, что интеграл от напряженности магнитного поля по любому замкнутому контуру (циркуляция вектора напряженности) равен алгебраической сумме токов, сцепленных с этим контуром:

(9.1)

причем положительными следует считать те токи, направление которых соответствует обходу контура по направлению движения часовой стрелки (правило буравчика). В частности, для контура на рис. 9.4 по закону полного

тока

Величина SI

в (9.1) называется магнитодвижущей силой (МДС).

Основной единицей МДС в системе СИ является ампер (А). Основная единица напряженности магнитного поля в системе СИ — ампер на метр (А/м) — особого наименования не имеет. Часто применяется также единица, кратная основной единице напряженности магнитного поля, — ампер на сантиметр, 1 А/см = 100 А/м.

Магнитную цепь большинства электротехнических устройств можно представить состоящей из совокупности участков, в пределах каждого из которых можно считать магнитное поле однородным, т. е. с постоянной напряженностью, равной напряженности магнитного поля Нk

вдоль средней линии участка длиной
lk
. Для таких магнитных цепей можно заменить интегрирование в (9.1) суммированием.

Если при этом магнитное поле возбуждается катушкой с током I

, у которой
w
витков, то для контура магнитной цепи, сцепленного с витками и состоящего из
n
участков, вместо (9.1) можно записать

(9.2 а),

Если контур сцеплен с витками m

катушек с токами, то

(9.2 б )

где Fp
=IpWp
— МДС.

Таким образом, согласно закону полного тока МДС F

равна сумме произведений напряженностей магнитного поля на длины соответствующих участков для контура магнитной цепи. Произведение
Hk·lk=Uмk
часто называют магнитным напряжением участка магнитной цепи.

Магнитное сопротивление и закон Ома для магнитной цепи.

По аналогии с электрической цепью величину

называют магнитным сопротивлением участка магнитной цепи (измеряется в 1/Гн).

Таким образом, магнитное напряжение

Выражение (3) по аналогии с электрической цепью часто называют
законом Ома для магнитной цепи Однако вследствие нелинейности цепи, вызванной непостоянством магнитной проницаемости μrферромагнетиков, оно практически не применяется для расчета магнитных цепей.

9.1.3. Свойства ферромагнитных материалов

Магнитное состояние любой точки изотропной среды, т. е. среды с одинаковыми свойствами во всех направлениях, вполне определяется вектором напряженности магнитного поля Н

и вектором магнитной индукции
В
, которые совпадают друг с другом по направлению.

Основная единица магнитной индукции в системе СИ называется тесла (Тл): 1 Тл = 1 Вб/м2 = 1 В·с/м2. Это индукция такого однородного магнитного поля, в котором магнитный поток Ф

через поверхность площадью 1 м2, перпендикулярную направлению магнитных линий поля, равен одному веберу (Вб).

В вакууме индукция и напряженность магнитного поля связаны простым соотношением: В = m0Н, где m 0 = 4p·10-7 Гн/м — магнитная постоянная. Для ферромагнитных материалов зависимость индукции от напряженности магнитного поля В(H)

в общем случае нелинейная.

Для того чтобы экспериментально исследовать магнитные свойства ферромагнитного материала, необходимо все измерения производить на образце, в котором магнитное поле однородное. Таким образцом может быть тороид, изготовленный из исследуемого ферромагнитного материала (рис. 9.5), длина магнитных линий в котором много больше его поперечных размеров (тонкостенный тороид). На тороиде находится равномерно навитая обмотка с числом витков w

.

Можно считать, что в тороиде из ферромагнитного изотропного материала с плотно намотанными витками все магнитные линии — окружности, а векторы напряженности и индукции магнитного поля направлены по касательной к соответствующей окружности. Так, на рис. 9.5 показаны средняя магнитная линия и векторы Н

и
В
в одной из ее точек.

При расчете напряженности и индукции магнитного поля в тонкостенном тороиде можно считать, что все магнитные линии имеют одинаковую длину, равную длине средней линии 2p
r
.

Предположим, что ферромагнитный материал тонкостенного тороида полностью размагничен и тока I

в обмотке нет (
В
= 0 и
Н
= 0). Если теперь плавно увеличивать постоянный ток
I
в обмотке катушки, то в ферромагнитном материале возникнет магнитное поле, напряженность которого определяется законом полного тока (9.1):

H
=Iw/2pr.
(9.3)

Каждому значению напряженности H

магнитного поля в тонкостенном тороиде соответствует определенная намагниченность ферромагнитного материала, а следовательно, и соответствующее значение магнитной индукции
В
.

Если начальное магнитное состояние материала тонкостенного тороида характеризуется значениями Н

= 0,
В
= 0, то при плавном нарастании тока получим нелинейную зависимость
В(Н),
которая называется кривой первоначального намагничивания (рис. 9.5, штриховая линия). Начиная с некоторых значений напряженности
H
магнитного поля индукция
В
в тонкостенном ферромагнитном тороиде практически перестает увеличиваться и остается равной
Вmax
. Эта область зависимости
В(Н)
называется областью технического насыщения.

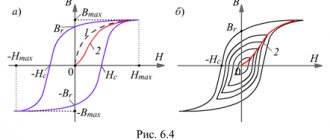
Если, достигнув насыщения, начать плавно уменьшать постоянный ток в обмотке, т. е. уменьшать напряженность поля (9.3), то индукция также начнет уменьшаться. Однако зависимость В(Н)

уже не совпадает с кривой первоначального намагничивания. Изменив направление тока в обмотке и увеличив его значение, получим новый участок зависимости
В(Н).
При значительных отрицательных значениях напряженности магнитного поля снова наступит техническое насыщение ферромагнитного материала. Если теперь продолжить эксперимент: сначала уменьшать ток обратного направления, затем увеличивать ток прямого направления до насыщения и т. д., то после нескольких циклов перемагничивания для зависимости
В(Н)
будет получена симметричная кривая (рис. 9.5, сплошная линия). Этот замкнутый цикл
В(Н)
называется предельной статической петлей гистерезиса (или предельным статическим циклом гистерезиса) ферромагнитного материала. Если во время симметричного перемагничивания область технического насыщения не достигается, то симметричная кривая
В(Н)
называется симметричной частной петлей гистерезиса ферромагнитного материала.

Предельный статистический цикл гистерезиса ферромагнитных материалов характеризуется следующими параметрами:

Нс

— коэрцитивной силой,
Вr
— остаточной индукцией и
k=Br/BH—l0Hc
— коэффициентом прямоугольности.

По значению параметра Hс

предельного статического цикла гистерезиса ферромагнитные материалы делятся на группы:

1) магнитные материалы с малыми значениями коэрцитивной силы (Hс

<� 0,05…0,01 А/м) называются магнитно-мягкими;

2) магнитные материалы с большими значениями коэрцитивной силы (Hс

> 20…30 кА/м) называются магнитно-твердыми.

Магнитно-твердые материалы используются для изготовления постоянных магнитов, а магнитно-мягкие — для изготовления магнитопроводов электротехнических устройств, работающих в режиме перемагничивания по предельному или частым циклам.

Магнитно-мягкие материалы в свою очередь делятся на три типа: магнитные материалы с прямоугольной предельной статической петлей гистерезиса, у которых коэффициент прямоугольности k

> 0,95 (рис. 9.6, а); магнитные материалы с округлой предельной статической петлей гистерезиса, у которых коэффициент прямоугольности 0,4 < <
k
< 0,7 (рис. 9.6, б); магнитные материалы с линейными свойствами, у которых зависимость
В(H)
практически линейная:
В =mrm0Н
(рис. 9.6, в), где
mr
— относительная магнитная проницаемость.

Все типы магнитных характеристик ферромагнитных материалов могут быть получены на образцах, изготовленных либо из различных ферромагнитных сплавов, либо из ферромагнитной керамики (ферриты). Ценное свойство ферритов в отличие от ферромагнитных сплавов — их высокое удельное электрическое сопротивление.

Магнитопроводы из ферромагнитных материалов с прямоугольным предельным статическим циклом гистерезиса применяются в оперативной памяти цифровых ЭВМ, магнитных усилителях и других устройствах автоматики. Ферромагнитные материалы с округлым предельным статическим циклом гистерезиса используются при изготовлении магнитопроводов электрических машин и аппаратов. Магнитопроводы этих устройств обычно работают в режиме перемагничивания по симметричным частным циклам. При основных расчетах магнитопроводов таких электротехнических устройств симметричные частные циклы заменяют основной кривой намагничивания ферромагнитного материала, которая представляет собой геометрическое место вершин симметричных частных циклов тонкостенного ферромагнитного тороида (рис. 9.7), полученных при синусоидальном токе низкой частоты в обмотке.

По основной кривой намагничивания ферромагнитного материала определяют зависимость абсолютной магнитной проницаемости

ma

=
mrm0
=
В/Н
(9.4)

от напряженности Н

магнитного поля, которая показана на рис. 9.7 штриховой линией.

На рис. 9.8 приведены основные кривые намагничивания некоторых электротехнических сталей, используемых в электрических машинах, трансформаторах и других устройствах, а также чугуна и пермаллоя.

Из ферромагнитных материалов с линейными свойствами изготовляют участки магнитопроводов для катушек индуктивности колебательных контуров с высокой добротностью. Такие контуры применяются в различных радиотехнических устройствах (приемниках, передатчиках), в малогабаритных антеннах средств связи и т. д.

Если на участке магнитопровода с площадью поперечного сечения S

магнитное поле неоднородное, то часто расчет можно вести, пользуясь средним значением индукции
Вср = Ф/S
и напряженностью
Нср
на средней магнитной линии. Например, для тороида с прямоугольной формой поперечного сечения, внутренним радиусом
rt,
внешним радиусом
r2
и высотой
h
, изготовленного из магнитного материала с линейными свойствами
В = mrm0H
при
mr
= const (рис. 9.6, в),

где

Из полученных выражений следует, что

В дальнейшем для упрощения расчетов неоднородность магнитного поля в поперечном сечении каждого участка магнитопровода учитывать не будем, и будем считать, что поле в каждом участке однородное и определяется значениями напряженности и индукции на средней магнитной линии.

Лекция по УД «Электротехника» на тему: «Электромагнетизм и магнитная индукция»

Раздел 2. Электромагнетизм и магнитная индукция

Тема 1. Электромагнетизм и магнитная индукция

Цель:

Знакомство с понятием магнитного поля, характеристиками и параметрами магнитного поля. с магнитной цепью. Изучение закона Ома и законов Кирхгофа для магнитной цепи, закона электромагнитной индукции, принципа Ленца. Определение энергии магнитного поля. Расчет магнитных цепей.

Задачи:

1. Ознакомиться с понятием магнитного поля, характеристиками и параметрами магнитного поля, с магнитной цепью. Рассмотреть закон Ома и законы Кирхгофа для магнитной цепи, закон электромагнитной индукции, принцип Ленца. Определить энергию магнитного поля. Научиться проводить расчет магнитных цепей.

2. Совершенствовать умение применять основные термины и формулы на практике.

3. Способствовать пониманию сущности и социальной значимости своей будущей профессии, проявлению к ней устойчивого интереса.

Информационное обеспечение:

Основная литература:

1. Синдеев Ю.Г. Электротехника с основами электроники: Учебник для учащихся профессиональных училищ и колледжей. — Ростов на Дону: Феникс, 2014.

2. Туревский И.С., Славинский А.К. Электротехника с основами электроники. Учебное пособие для СПО. – М.: Форум, 2014.

Дополнительная литература:

1. Данилов И.А. Общая электротехника с основами электроники. — М.: Высшая школа, 2012.

2. Ермуратский П.В. Электротехника и электроника. – М.: ДМК Пресс, 2011.

3. Касаткин А.С. Основы электротехники. – М.: Высшая школа, 2001.

Интернет-ресурсы:

http:/antigtu.ru/video-l-p/ — видеолекции по электротехнике; электронные лекции по электротехнике; готовые решения задач из различных задачников.

Содержание

1.

Понятие магнитного поля.

2.

Характеристики и параметры магнитного поля.

3.

Магнитная цепь.

4.

Закон Ома и законы Кирхгофа для магнитной цепи.

5.

Закон электромагнитной индукции. Принцип Ленца.

6.

Энергия магнитного поля.

7.

Расчет магнитных цепей.

1.
Понятие магнитного поля
Основные магнитные явления.

С древних времен было известно, что некоторые виды железной руды обладают свойством притягивать к себе железо. Такую руду назвали магнитом.

Свое влияние магнит оказывает не только на подносимые к нему предметы, но и на окружающее его пространство. Если вокруг линейного магнита расположить маленькие магнитные стрелки, увидим, что по отношению к магниту они расположились по-разному. Убрав магнит, увидим, что все стрелки устанавливаются приблизительно в направлении север— юг. Следовательно, присутствие магнита меняет свойства пространства вокруг него.

Рисунок 1. Расположение магнитных силовых линий постоянного магнита

Пространство, в котором обнаруживается действие магнита на магнитную стрелку, называют магнитным полем, а линию, по которой устанавливают ось магнитной стрелки, называют магнитной силовой линией. Принято считать, что силовые линии выходят из северного полюса и входят в южный.

Магнитное поле электрического тока.

Магнитные и электрические явления имеют тесную связь между собой. В этом легко убедиться на следующем опыте. Установив над магнитной стрелкой параллельно ей провод и пропустив по нему электрический ток, заметим, что стрелка отклонится от своего прежнего положения. Но как только прекращается ток, стрелка снова возвращается в первоначальное положение.

Из этого опыта можно сделать вывод, что при прохождении тока по проводнику вокруг последнего образуется магнитное поле: магнитная стрелка отклоняется током.

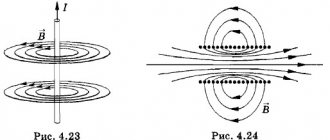
Если вокруг проводника, по которому проходит электрический ток, поместить несколько магнитных стрелок, все стрелки будут поворачиваться и устанавливаться по направлению касательных к окружностям: силовые линии магнитного поля прямолинейного тока представляют собой замкнутые концентрические окружности, расположенные в плоскостях, перпендикулярных направлению тока. При изменении направления тока в проводнике все магнитные стрелки повернутся и станут в противоположном направлении.

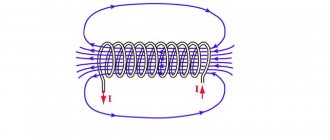
Соленоидом

называют свитый спиралью проводник, по которому пропущен электрический ток. Если соленоид приблизить к магнитной стрелке, увидим, что один конец соленоида притягивает южный, а другой — северный полюс. Следовательно, соленоид при прохождении по нему тока по своим магнитным свойствам подобен прямому магниту. Направление магнитных силовых линий и полюсов соленоида определяют с помощью «правила винта».

Если внутрь соленоида ввести сердечник из мягкого железа, а соленоид значительно отодвинуть от магнитной стрелки, стрелка компаса все же повернется. Это говорит о том, что железный сердечник усиливает магнитное действие соленоида.

Электромагнит.

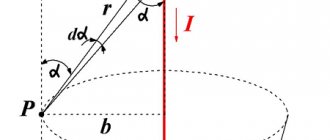
Соленоид, внутри которого находится стальной сердечник, называют электромагнитом. Электромагниты широко применяют в технике. С их помощью создаются магнитные поля в электрических генераторах, электроизмерительных приборах, реле и т. д.

2.
Характеристики и параметры магнитного поля
Магнитная проницаемость.

Способность любого материала намагничиваться в той или другой степени определяется его магнитной проницаемостью. Магнитная проницаемость ферромагнитных материалов различна и превышает магнитную проницаемость вакуума (магнитную постоянную). Число, показывающее, вo сколько раз магнитная проницаемость ферромагнитного материала больше магнитной проницаемости вакуума, называют
относительной магнитной проницаемостью
.

Пропуская ток по катушке с сердечником, создаем магнитное поле. Следовательно, сердечник катушки намагничивается. Чем больше сила тока и количество витков в катушке, тем больше намагничивается сердечник. Значит, величина намагничивающей силы равна произведению силы тока на количество витков проводника в катушке.

Напряженность.

Магнитное поле, создаваемое проводником при прохождении по нему тока, характеризуется напряженностью, которую определяют при делении намагничивающей силы на длину катушки и обозначают
1 А/м
. Однако в практике обычно применяют другую единицу измерения, в
80 раз
большую, чем
1 А/м
, называемую
эрстедом
.

Интенсивность или силу воздействия поля оценивают величиной вектора магнитной индукции

. Она определяется значением силы «F», создаваемой проходящим током «I» по проводнику длиной «l». В=F/(I∙l)

Единица измерения магнитной индукции в системе СИ — Тесла (в знак памяти об ученом физике, который исследовал эти явления и описал их математическими методами). В русской технической литературе она обозначается «Тл», а в международной документации принят символ «Т».

1 Тл — это индукция такого однородного магнитного потока, который воздействует с силой в 1 ньютон на каждый метр длины прямолинейного проводника, перпендикулярно расположенного направлению поля, когда по этому проводнику проходит ток 1 ампер.

1Тл=1∙Н/(А∙м)

Направление вектора определяется по правилу левой руки (Рисунок 2).

Рисунок 2. Правило
определениянаправления вектора магнитной индукции
Если расположить ладонь левой руки в магнитном поле так, чтобы силовые линии из северного полюса входили в ладонь под прямым углом, а четыре пальца расположить по направлению тока в проводнике, то оттопыренный большой палец укажет направление действия силы на этот проводник.

Сила, воздействующая на электрический ток, не зависит от материалов, из которых создан проводник и площади его сечения. Даже если этого проводника вообще не будет, а движущиеся заряды станут перемещаться в другой среде между магнитными полюсами, то эта сила никак не изменится.

Если внутри магнитного поля во всех точках вектор имеет одинаковое направление и величину, то такое поле считают равномерным.

Магнитный поток (Ф)

Если рассматривать прохождение магнитной индукции через определенную площадь S, то ограниченная ее пределами индукция будет называться магнитным потоком (рисунок 3).

Рисунок 3. Иллюстрация определения величины магнитного потока

Когда площадь наклонена под каким-то углом α к направлению магнитной индукции, то магнитный поток уменьшается на величину косинуса угла наклона площади. Максимальное же его значение создается при перпендикулярном расположении площади к ее пронизывающей индукции. Ф=В·S

Единицей измерения магнитного потока является 1 вебер, определяемый прохождением индукции в 1 теслу через площадь в 1 метр квадратный.

Электромагнитная индукция.

Мы уже установили, что ток производит магнитное действие: магнитная стрелка отклоняется под влиянием тока, проходящего по проводнику; железный стержень, помещенный внутри катушки с током, намагничивается; проводник с током, находясь в магнитном поле, приходит в движение.

Однако возможным оказывается обратное действие. При некоторых условиях магнитное поле может возбуждать электрический ток. При движении проводника в магнитном поле или изменении магнитного потока вокруг него в проводнике индуктируется (наводится) электродвижущая сила (э.д.с.

), под действием которой в замкнутом проводнике образуется электрический ток. Было установлено, что электрический ток возникает в проводнике, если проводник и магнит движутся относительно друг друга. Но индукционный ток возникает и проводнике только при условии, что проводник при своем движении пересекает магнитные силовые линии. Если проводник движется вдоль силовых линий, не пересекая их, ток в нем не возникает. Индукционный ток возникает также в том случае, если вокруг проводника изменяется величина магнитного потока.

Возникновение электрического тока в замкнутом проводнике при пересечении им магнитных силовых линий называют электромагнитной индукцией, возникающая электродвижущая сила (э.д.с

)—
индукционной
, а ток —
индукционным
.

Самоиндукция.

При замыкании и размыкании электрической цепи вокруг проводника создается и исчезает магнитное поле. Изменяющееся магнитное поле пересекает проводник и создает в нем электродвижущую силу самоиндукции —
э.д.с. самоиндукции
. При всяком изменении «собственного» магнитного поля проводника он пересекается «собственными магнитными» линиями и в нем возникает э.д.с. самоиндукции.

Индуктивность электрической цепи измеряется в генри

(
Гн
). Проводник обладает индуктивностью в
1 Гн
, если при равномерном изменении тока в проводнике на
1 А
в
1 сек
в нем наводится э.д.с. самоиндукции, равная
1 В
.

Взаимоиндукция.

Возьмем два проводника, намотаем из них две катушки, расположим эти катушки на некотором расстоянии друг от друга и по одной из катушек пропустим изменяющийся ток. Тогда магнитное поле, созданное этим током, пересечет витки второй катушки, в которой возникнет э.д.с. взаимоиндукции, а следовательно, и электрический ток взаимоиндукции. Ток в свою очередь послужит причиной появления магнитного поля, которое пересечет витки первой катушки, вызвав в ней также э.д.с взаимоиндукции. Этот процесс называют взаимной индукцией.

3.
Магнитная цепь
Магнитной цепью

называют устройство, в котором замыкается магнитный поток. Магнитная цепь – это совокупность ферромагнитных и неферромагнитных частей электротехнических устройств, необходимых для создания магнитных полей нужных конфигураций и интенсивности.

В зависимости от принципа действия электротехнического устройства магнитное поле может возбуждаться либо постоянным магнитом, либо катушкой с током, расположенной в той или иной части магнитной цепи. Электромагнитные процессы в магнитной цепи описываются с помощью следующих понятий: магнитодвижущая сила (МДС – F

), магнитный поток (Ф), магнитное напряжение (
U
м) и др.

Магнитные цепи могут быть неразветвленные

, в которых магнитный поток в любом сечении цепи одинаков, и
разветвленные
, в которых магнитные потоки в различных сечениях цепи различны.

Таблица 1. Схемы
разветвленной и неразветвленноймагнитной цепи

Разветвленные магнитные цепи могут быть сложной конфигурации, например в электрических двигателях, генераторах и других устройствах.

Неразветвленные магнитные цепи бывают однородные

и
неоднородные
Однородная

магнитная цепь образует замкнутый магнитопровод с равномерной намагничивающей обмоткой, причем каждый виток обмотки создает линии магнитной индукции, которые, замыкаясь по магнитопроводу, сливаются в общий магнитный поток.

В такой цепи магнитные линии проходят в одной среде и напряженность магнитного поля вдоль линий не меняется. Как правило, это – кольцевые магнитопроводы (тороиды), которые используют в качестве стандартных образцов, применяемых для определения магнитных характеристик материалов.

Неоднородная

магнитная цепь – это такая магнитная цепь, в которой магнитопровод не сплошной, а, например, с воздушным зазором, поэтому магнитный поток и напряженность магнитного поля в ферромагнитном материале и воздушном зазоре – различны.

Магнитопровод это путь, по которому замыкается магнитный поток. Этот путь может проходить целиком по воздуху.

На рисунке 4,а показан соленоид. Магнитная цепь здесь проходит через воздух. Магнитное сопротивление воздуха очень велико, поэтому даже при большой намагничивающей силе магнитный поток мал.

Для увеличения магнитного потока в состав магнитной цепи вводят ферромагнитные материалы (обычно литая или электротехническая сталь), имеющие меньшее магнитное сопротивление.

На рисунке 4,б

представлен прямой электромагнит с разомкнутым сердечником. Магнитные линии только небольшую часть своего пути проходят по стальному сердечнику, большую же часть своего пути они проходят по воздуху. Полюсы электромагнита определяются при помощи «правила буравчика».

Подковообразный электромагнит, изображенный на рисунке 4,в

, представляет магнитную цепь с лучшими условиями для прохождения магнитного потока. При такой конструкции поток большую часть пути проходит по стали и меньшую часть от полюса
N
до полюса
S
по воздуху.

На рисунке 4,г

представлена конструкция магнитной цепи, применяемая в электромашиностроении и приборостроении. Между полюсами электромагнита помещается стальной якорь. Большую часть своего пути магнитные линии проходят по стали и только очень малую часть (от нескольких долей миллиметра до 2–3 мм) проходят по двум воздушным промежуткам.

4.
Закон Ома и законы Кирхгофа для магнитной цепи
Закон Ома:

магнитное напряжение на любом участке

т.к..

Если ,

то
,
где
—
магнитное сопротивление
..
Магнитный поток прямо пропорционален магнитному напряжению и обратно пропорционален магнитному сопротивлению.

Законы Кирхгофа

Первый закон Кирхгофа для магнитных цепей

гласит: алгебраическая сумма
магнитных потоков
в узле магнитной цепи равна нулю .

Первый закон Кирхгофа применяют к магнитным узлам разветвленной магнит­ной цепи (рисунок 5).

Рисунок 5. Распределение магнитных потоков

Второй закон Кирхгофа для магнитных цепей

сформулируем следующим образом: алгебраическая сумма
магнитных напряжений UM
=
H
·
l
в замкнутом контуре магнитной цепи (∑UM=∑H⋅l) равна алгебраической сумме
магнитодвижущих силF
=
I
·
w
в том же контуре (∑F=∑I⋅w):

∑UM=∑F

или

∑H⋅l=∑I⋅w.

5.
Закон электромагнитной индукции. Правило Ленца
В 1831 г. Фарадей открыл одно из наиболее фундаментальных явлений в электродинамике – явление электромагнитной индукции: в замкнутом проводящем контуре при изменении магнитного потока через поверхность, опирающуюся на этот контур, возникает электрический ток (индукционный ток).

Было установлено, что индукционный ток всегда имеет такое направление, что он препятствует изменению магнитного потока через данный проводящий контур. Эту закономерность называют правилом Ленца

.

Рисунок 6. Иллюстрация правила Ленца

В том случае, когда мы вводим магнит в катушку(рисунок 6), магнитный поток в контуре увеличивается, а значит магнитное поле, создаваемое индуцируемым током, по правилу Ленца направлено против увеличения поля магнита. Чтобы определить направление тока, нужно посмотреть на магнит со стороны северного полюса. С этой позиции мы будем вкручивать буравчик по направлению магнитного поля тока, то есть навстречу северному полюсу. Ток будет двигаться по направлению вращения буравчика, то есть по часовой стрелке.

В том случае, когда мы выводим магнит из катушки, магнитный поток в контуре уменьшается, а значит магнитное поле, создаваемое индуцируемым током, направлено против уменьшения поля магнита. Чтобы определить направление тока, нужно выкручивать буравчик, направление вращения буравчика укажет направление тока в проводнике – против часовой стрелки.

Появление индукционного тока означает, что при изменении магнитного потока в контуре возникает ЭДС (ЭДС индукции) Ei

. Фарадей установил, что ЭДС индукции не зависит от того, каким способом осуществляется изменение магнитного потока: изменяется площадь контура, его ориентация в магнитном поле, или меняется во времени магнитное поле, пронизывающее неподвижный контур. Во всех случаях при изменении внешнего магнитного потока, пронизывающего контур, в контуре возникает индукционный ток. При этом значение электродвижущей силы численно равно скорости изменения магнитного потока, взятой со знаком «-».

где Ф – магнитный поток через контур.

Эта формула выражает закон электромагнитной индукции

и «автоматически» учитывает правило Ленца. При использовании формулы (1) направление нормали к поверхности, ограниченной контуром, можно выбирать произвольно, а направление обхода контура должно быть связано с направлением нормали правилом правого винта. Тем самым определены и знак магнитного потока, и «направление» ЭДС индукции в контуре.

6.
Энергия магнитного поля
Энергия магнитного поля

показывает, какую работу затратил электрический ток в проводнике (катушке индуктивности) на создание этого магнитного поля. Естественно эта энергия будет напрямую зависеть от индуктивности проводника, вокруг которого магнитное поле создается.

Оказывается, энергия магнитного поля равна половине про­изведения индуктивности цепи на квадрат силы тока, т. е.

8.
Расчет магнитных цепей
Магнитная цепь подобна электрической цепи. Магнитный поток Ф напоминает электрический ток I, индукция B напоминает плотность тока, намагничивающая сила (н. с.) Fм (H∙l=I∙ω) соответствует э. д. с.

В простейшем случае магнитная цепь имеет везде одинаковое сечение и выполнена из однородного магнитного материала. Для определения намагничивающей силы (н. с.) I∙ω, необходимой для обеспечения требуемой индукции B, по кривой намагничивания определяют соответствующую напряженность H и умножают ее на среднюю длину
магнитной силовой линии l:
Fм =H∙l=I∙ω

.

Отсюда определяют требуемый ток I или число витков ω катушки.

Сложная магнитная цепь обычно имеет участки с разными сечениями и магнитными материалами. Эти участки обычно соединены последовательно, поэтому по каждому из них проходит одинаковый магнитный поток Ф. Индукция B на каждом участке зависит от сечения участка и рассчитывается для каждого участка в отдельности по формуле B=Ф∶S.

Для разных значений индукции по кривой намагничивания (рисунок ?) определяют напряженность H и умножают ее на среднюю длину силовой линии соответствующего участка цепи. Суммируя отдельные произведения, получают полную н. с. магнитной цепи:

Fм=I∙ω=H1 ∙l1+H2 ∙l2+H3 ∙l3+…,

по которой определяют намагничивающий ток или число витков катушки.

Рисунок 7. Кривые намагниченности

Примеры

1. Каким должен быть намагничивающий ток I катушки, имеющей 200 витков, чтобы ее н. с. создала в чугунном кольце магнитный поток:

Ф=15700 Мкс =0,000157 Вб?

Средний радиус чугунного кольца r=5 см, а диаметр его сечения d=2 см (рисунок 8).

Рисунок 8. Схема замкнутой магнитной цепи

Сечение магнитной цепи S=(π∙d2)/4=3,14 см2.

Индукция в сердечнике равна: B=Ф∶S=15700∶3,14=5000 Гс.

В системе МКСА индукция равна: B=0,000157 Вб :0,0000314 м2 =0,5 Тл.

По кривой намагничивания чугуна находим для B=5000 Гс =0,5 Тл требуемую напряженность H, равную 750 А/м. Намагничивающая сила равна: I∙ω=H∙l=235,5 Ав.

Отсюда требуемый ток I=(H∙l)/ω=235,5/200=1,17 А.

2. Замкнутая магнитная цепь (рисунок 9) выполнена из пластин трансформаторной стали. Сколько витков должна иметь катушка с током 0,5 А, чтобы создать в сердечнике магнитный поток Ф=160000 Мкс =0,0016 Вб?

Рисунок 9. Схема замкнутой магнитной цепи

Сечение сердечника S=4∙4=16 см2 =0,0016 м2.

Индукция в сердечнике B=Ф/S=160000/16=10000 Гс =1 Тл.

По кривой намагничивания трансформаторной стали находим для B=10000 Гс =1 Тл напряженность H=3,25 А/см =325 А/м.

Средняя длина магнитной силовой линии l

=2∙(60+40)+2∙(100+40)=480=0,48 м.

Намагничивающая сила Fм=I∙ω=H∙l=3,25∙48=315∙0,48=156 Ав.

При токе 0,5 А число витков ω=156/0,5=312.

3. Магнитная цепь, изображенная на рисунке10, аналогична магнитной цепи предыдущего примера, за исключением того, что она имеет воздушный зазор δ=5 мм. Какими должны быть н. с. и ток катушки, чтобы магнитный поток был таким же, как и в предыдущем примере, т. е. Ф=160000 Мкс = 0,0016 Вб?

Рисунок 10. Схема разомкнутой магнитной цепи

Магнитная цепь имеет два последовательно соединенных участка, сечение которых такое же, как и в предшествующем примере, т. е. S=16 см2. Индукция также равна B=10000 Гс =1 Тл.

Средняя длина магнитной линии в стали немного меньше:

lс=48-0,5=47,5 см ≈0,48 м.

Магнитное напряжение на этом участке магнитной цепи

Hс ∙lс=3,25∙48≈156 Ав.

Напряженность поля в воздушном зазоре равна:

Hδ=0,8∙B=0,8∙10000=8000 А/см.

Магнитное напряжение на участке воздушного зазора Hδ∙δ=8000∙0,5=4000 Ав.

Полная н. с. равна сумме магнитных напряжений на отдельных участках: I∙ω=Hс ∙lс+Hδ∙δ=156+4000=4156 Ав. I=(I∙ω)/ω=4156/312=13,3 А.

Если в предыдущем примере необходимый магнитный поток обеспечивался током 0,5 А, то для магнитной цепи с воздушным зазором 0,5 см требуется ток 13 А, чтобы получить тот же магнитный поток. Отсюда видно, что воздушный зазор, даже незначительный по отношению к длине магнитопровода, сильно увеличивает необходимые н. с. и ток катушки.

Контрольные вопросы

1. Что называют магнитным полем?

2. Составной частью какого поля является магнитное поле?

3. Что называют магнитной индукцией и в чем ее измеряют?

4. От чего зависит магнитная индукция в точке?

5. От чего зависит сила электромагнитного воздействия на проводник?

6. От чего зависит электромагнитная сила двух проводников с током?

7. Что называют магнитным потоком и в чем его измеряют?

8. Что характеризует относительная магнитная проницаемость?

9. Что такое напряженность магнитного поля ?

10. Что называют электромагнитной индукцией?

11. Каков закон электромагнитной индукции?

12. Сформулируйте правило Ленца при возникновении индукционного тока.

13. Что такое ЭДС самоиндукции?

14. Что называют процессом взаимной индукции?

9.1.4. Неразветвленная магнитная цепь

Задачей расчета неразветвленной магнитной цепи в большинстве случаев является определение МДС F
=Iw
, необходимой для того, чтобы получить заданные значения магнитного потока или магнитной индукции в некотором участке магнитопровода (чаще всего в воздушном зазоре).

На рис. 9.9 приведен пример неразветвленной магнитной цепи — магнитопровод постоянного поперечного сечения S1

с зазором. На этом же рисунке указаны другие геометрические размеры обоих участков магнитопровода: средняя длина
l1
магнитной линии первого участка из ферромагнитного материала и длина
l2
второго участка — воздушного зазора. Магнитные свойства ферромагнитного материала заданы основной кривой намагничивания
В(Н)
(рис. 9.10) и тем самым по (9.4) зависимостью
ma(Н).
По закону полного тока (9.2)

где H1

и
H2
— напряженности магнитного поля в первом и втором участках.

В воздушном зазоре значения магнитной индукции В2

и напряженности
H2
связаны простым соотношением
В2
=
m0Н2
, а для участка из ферромагнитного материала
В1
=
ma1Н1.
Кроме того, в неразветвленной магнитной цепи магнитный поток одинаков в любом поперечном сечении магнитопровода:

Ф
= В1S1=B2S2,
(9.6)

где S1

и
S2
— площади поперечного сечения участка из ферромагнитного материала и воздушного зазора.

Если задан магнитный поток Ф

, то по (9.6) найдем значения индукций
B1
и
B2
. Напряженность поля
H1
определим по основной кривой намагничивания (рис. 9.10), а
H2
=
B2
/
m0
. Далее по (9.5) вычислим необходимое значение МДС.

Сложнее обратная задача: расчет магнитного потока при заданной МДС F

.

Заменив в (9.5) напряженности магнитного поля значениями индукции, получим

,

или с учетом (9.6)

где rMk
=lk/Skmak
— магнитное сопротивление
k
-гo участка магнитной цепи, причем магнитное сопротивление
k
-гo участка нелинейное, если зависимость
В(H)
для этого участка нелинейная (рис. 9.10), т.е.
mak
≠ const.

Для участка цепи с нелинейным магнитным сопротивлением rM

можно построить вебер-амперную характеристику — зависимость магнитного потока
Ф
от магнитного напряжения
UM
на этом участке магнитопровода. Вебер-амперная характеристика участка магнитопровода рассчитывается по основной кривой намагничивания ферромагнитного материала
В(H)
. Чтобы построить вебер-амперную характеристику, нужно ординаты и абсциссы всех точек основной кривой намагничивания умножить соответственно на площадь поперечного сечения участка
S
и его среднюю длину
l
.

На рис. 9.11 приведены вебер-амперные характеристики Ф

(
UM1
) для ферромагнитного участка с нелинейным магнитным сопротивлением
rM1
и
Ф
(
UM
2) для воздушного зазора с постоянным магнитным сопротивлением
rM
2 =
l2/S2m0
магнитопровода по рис. 9.9.

Между расчетами нелинейных электрических цепей постоянного тока и магнитных цепей с постоянными МДС нетрудно установить аналогию. Действительно, из уравнения (27.7) следует, что магнитное напряжение на участке магнитной цепи равно произведению магнитного сопротивления участка на магнитный поток UM

=
rMФ
. Эта зависимость аналогична закону Ома для резистивного элемента электрической цепи постоянного тока
U = rI
. Сумма магнитных напряжений в контуре магнитной цепи равна сумме МДС этого контура
SUM
=
SF
, что аналогично второму закону Кирхгофа для электрических цепей постоянного тока
SU
=
SE.
Продолжая дальше аналогию между электрическими цепями постоянного тока и магнитными цепями с постоянными МДС, представим неразветвленную магнитную цепь (рис. 9.9) схемой замещения (рис. 9.12, а).

В качестве иллюстрации ограничимся применением для анализа неразветвленной магнитной цепи графических методов: метода сложения вебер-амперных характеристик (рис. 9.11) и метода нагрузочной характеристики (рис. 9.12, б).

Согласно первому методу построим вебер-амперную характеристику всей неразветвленной магнитной цепи Ф

(
UM1
+
UM
2), графически складывая по напряжению вебер-амперные характеристики ее двух участков. При известной МДС
F=Iw
по вебер-амперной характеристике всей магнитной цепи определим рабочую точку
А
, т. е. магнитный поток
Ф
, а по вебер-амперным характеристикам участков магнитопровода — магнитные напряжения на каждом из них.

Согласно второму методу для второго (линейного) участка построим нагрузочную характеристику

т. е. прямую, проходящую через точку F

на оси абсцисс и точку
F
/
rM2
на оси ординат. Точка пересечения
А
нагрузочной характеристики с вебер-амперной характеристикой ферромагнитного участка цепи Ф(
UM1
) определяет магнитный поток
Ф
в цепи и магнитные напряжения на ферромагнитном участке
UM1
и воздушном зазоре
UM2
. Значение индукции в воздушном зазоре
B2= Ф/S2
.

Основные параметры магнитных цепей

Из курса физики известно, что любой проводник с током наводит вокруг себя магнитное поле. Таким образом, в пространстве, окружающем движущиеся электрические заряды и постоянные магниты, возникает магнитное поле.

В веществе магнитное поле возбуждается не только электрическими токами, текущими по проводам, но и движением заряженных частиц внутри самих атомов и молекул.

Магнитное поле в веществе может быть микроскопическим и макроскопическим. Микроскопическое поле – это истинное поле, возбуждаемое движущимися элементарными зарядами вещества. Оно резко меняется на расстоянии атомного масштаба. Макроскопическое поле получается из микроскопического путем сглаживания, то есть усреднения по физически бесконечно малым объемам пространства.

Магнитное поле наглядно изображается магнитными силовыми линиями, которые задают направление магнитного поля в пространстве. Эти линии не имеют ни начала, ни конца, то есть являются замкнутыми.

В пространстве, окружающем магнит за положительное направление силовых линий принято направление от северного полюса к южному. Чем сильнее магнитное поле, тем выше плотность силовых линий. Магнитное поле можно определить с помощью магнитной стрелки, которая в каждой точке поля устанавливается по касательной к силовой линии магнитного поля.

Силовые линии магнитного поля прямолинейного проводника с током имеют вид концентрических окружностей (рис. 16.1).

Магнитодвижущая сила (MMF)

Основная статья: магнитодвижущая сила

Подобно тому, как электродвижущая сила (ЭДС) управляет током электрического заряда в электрических цепях, магнитодвижущая сила (MMF) «управляет» магнитным потоком через магнитные цепи. Термин «магнитодвижущая сила», однако, неверен, поскольку это не сила и не что-либо движущееся. Возможно, лучше называть это просто MMF. По аналогии с определением ЭДС, магнитодвижущая сила F { Displaystyle { mathcal {F}}} вокруг замкнутого цикла определяется как:

F = ∮ ЧАС ⋅ d л . { displaystyle { mathcal {F}} = oint mathbf {H} cdot mathrm {d} mathbf {l}.}

MMF представляет собой потенциал, который гипотетический магнитный заряд выиграет, завершив цикл. Управляемый магнитный поток равен нет

ток магнитного заряда; он просто имеет такое же отношение к MMF, как электрический ток к EMF. (См. Подробное описание микроскопических источников сопротивления ниже.)

Единицей магнитодвижущей силы является ампер-виток (At), представленный устойчивым прямым электрический ток одного ампер протекающий в одновитковой петле электропроводящего материала в вакуум. Гилберт (Gb), установленный IEC в 1930 г.[1] это CGS единица магнитодвижущей силы и является единицей немного меньшей, чем ампер-виток. Апартамент назван в честь Уильям Гилберт (1544–1603) английский врач и натурфилософ.

1 Гб = 10 4 π В ≈ 0.795775 В { displaystyle { begin {align} 1 ; { text {Gb}} & = { frac {10} {4 pi}} ; { text {At}} & приблизительно 0,795775 ; { text {At}} end {align}}} [2]

Магнитодвижущую силу часто можно быстро рассчитать, используя Закон Ампера. Например, магнитодвижущая сила F { Displaystyle { mathcal {F}}} длинной катушки составляет:

F = N я { displaystyle { mathcal {F}} = NI}

куда N

это количество повороты и
я
это ток в катушке. На практике это уравнение используется для MMF реальных индукторы с
N
будучи номер намотки индукционной катушки.