Электромагниты
Однажды, в очередной раз, перелистывая книгу, которую нашел у мусорного бачка, обратил внимание на простой, приблизительный расчет электромагнитов. Титульный лист книги показан на фото1.
Вообще их расчет это сложный процесс, но для радиолюбителей, расчет, приведенный в этой книге, вполне подойдет. Электромагнит применяется во многих электротехнических приборах. Он представляет собой катушку из проволоки, намотанной на железный сердечник, форма которого может быть различной. Железный сердечник является одной частью магнитопровода, а другой частью, с помощью которой замыкается путь магнитных силовых линий, служит якорь. Магнитная цепь характеризуется величиной магнитной индукции — В, которая зависит от напряженности поля и магнитной проницаемости материала. Именно поэтому сердечники электромагнитов делают из железа, обладающего высокой магнитной проницаемостью. В свою очередь, от магнитной индукции зависит силовой поток, обозначаемый в формулах буквой Ф. Ф = В • S — магнитная индукция — В умноженная на площадь поперечного сечения магнитопровода — S. Силовой поток зависит также от так называемой магнитодвижущей силы (Ем), которая определяется числом ампервитков на 1см длины пути силовых линий и может быть выражена формулой: Ф = магнитодвижущая сила (Ем) • магнитное сопротивление (Rм) Здесь Ем = 1,3•I•N, где N — число витков катушки, а I — сила текущего по катушке тока в амперах. Другая составляющая: Rм = L/M•S, где L — средняя длина пути силовых магнитных линий, М — магнитная проницаемость, a S — поперечное сечение магнитопровода. При конструировании электромагнитов весьма желательно получить большой силовой поток. Добиться этого можно, если уменьшить магнитное сопротивление. Для этого надо выбрать магнитопровод с наименьшей длиной пути силовых линий и с наибольшим поперечным сечением, а в качестве материала — железоматериал с большой магнитной проницаемостью. Другой путь увеличения силового потока путем увеличения ампервитков не является приемлемым, так как в целях экономии проволоки и питания следует стремиться к уменьшению ампервитков. Обычно расчеты электромагнитов делаются по специальным графикам. В целях упрощения в расчетах мы будем также пользоваться некоторыми выводами из графиков. Предположим, требуется определить ампервитки и силовой поток замкнутого железного магнитопровода, изображенного на рисунке 1,а и сделанного из железа самого низкого качества.
Рассматривая график (к сожалению я его в приложении не нашел) намагничивания железа, нетрудно убедиться, что наиболее выгодной является магнитная индукция в пределах от 10 000 до 14 000 силовых линий на 1 см2, что соответствует от 2 до 7 ампервиткам на 1 см. Для намотки катушек с наименьшим числом витков и более экономичных в смысле питания для расчетов надо принимать именно эту величину (10 000 силовых линий на 1 см2 при 2 ампервитках на 1 см длины). В этом случае расчет может быть произведен следующим образом. Так, при длине магнитопровода L =L1+L2 равной 20 см + 10 см = 30 см, потребуется 2×30=60 ампервитков. Если диаметр D сердечника (Рис.1,в)примем равным 2 см, то его площадь будет равна: S = 3,14xD2/4 = 3,14 см2. 0тсюда возбуждаемый магнитный поток будет равен: Ф = B х S= 10000 x 3,14=31400 силовых линий. Можно приближенно вычислить и подъемную силу электромагнита (P). P = B2 • S/25 • 1000000 = 12,4 кг. Для двухполюсного магнита этот результат следует удвоить. Следовательно, Р=24,8 кг = 25 кг. При определении подъемной силы необходимо помнить, что она зависит не только от длины магнитопровода, но и от площади соприкосновения якоря и сердечника. Поэтому якорь должен точно прилегать к полюсным наконечникам, иначе даже малейшие воздушные прослойки вызовут сильное уменьшение подъемной силы. Далее производится расчет катушки электромагнита. В нашем примере подъемная сила в 25 кг обеспечивается 60 ампервитками. Рассмотрим, какими средствами можно получить произведение N•J = 60 ампервиткам. Очевидно, этого можно добиться либо путем использования большого тока при малом количестве витков катушки, например 2 А и 30 витков, либо путем увеличения числа витков катушки при уменьшении тока, например 0,25 А и 240 витков. Таким образом, чтобы электромагнит имел подъемную силу в 25 кг, на его сердечник можно намотать и 30 витков и 240 витков, но при этом изменить величину питающего тока. Конечно, можно выбрать и другое соотношение. Однако изменение величины тока в больших пределах не всегда возможно, так как оно обязательно потребует изменения диаметра применяемой проволоки. Так, при кратковременной работе (несколько минут) для проводов диаметром до 1 мм допустимую плотность тока, при которой не происходит сильного перегревания провода, можно принять равной 5 а/мм2. В нашем примере проволока должна быть следующего сечения: для тока в 2 а — 0,4 мм2, а для тока в 0,25 а — 0,05 мм2, диаметр проволоки будет 0,7 мм или 0,2 мм соответственно. Каким же из этих проводов следует производить обмотку? С одной стороны, выбор диаметра провода может определяться имеющимся ассортиментом проволоки, с другой — возможностями источников питания, как по току, так и по напряжению. Действительно, две катушки, одна из которых изготовлена из толстой проволоки в 0,7 мм и с небольшим числом витков — 30, а другая — из проволоки в 0,2 мм и числом витков 240, будут иметь резко различное сопротивление. Зная диаметр проволоки и ее длину, можно легко определить сопротивление. Длина проволоки L равна, произведению общего числа витков на длину одного из них (среднюю): L = N x L1 где L1 — длина одного витка, равная 3,14 x D. В нашем примере D = 2 см, и L1 = 6,3 см. Следовательно, для первой катушки длина провода будет 30 x 6,3 = 190 см, сопротивление обмотки постоянному току будет примерно равно ? 0,1 Ом, а для второй — 240 x 6,3 = 1 512 см, R ? 8,7 Ом. Пользуясь законом Ома, нетрудно вычислить необходимое напряжение. Так, для создания в обмотках тока в 2А необходимое напряжение равно 0,2В, а для тока в 0,25А — 2,2В. Таков элементарный расчет электромагнитов. Конструируя электромагниты, надо не только производить указанный расчет, но и уметь выбрать материал для сердечника, его форму, продумать технологию изготовления. Удовлетворительными материалами для изготовления сердечников в кружках являются прутковое железо (круглое и полосовое) и различные. железные изделия: болты, проволока, гвозди, шурупы и т. д. Чтобы избежать больших потерь на токах Фуко, сердечники для приборов переменного тока необходимо собирать из изолированных друг от друга тонких листов железа или проволоки. Для придания железу «мягкости» его необходимо подвергать отжигу. Большое значение имеет и правильный выбор формы сердечника. Наиболее рациональные из них кольцевые и П-образные. Некоторые из распространенных сердечников показаны на рисунке 1.
Просмотров:40 340
Метки: Электромагнит
Электромагнит применяется во многих электротехнических приборах. Он представляет собой катушку из проволоки, намотанной на железный сердечник, форма которого может быть различной. Железный сердечник является одной частью магнитопровода, а другой частью, с помощью которой замыкается путь магнитных силовых линий, служит якорь. Магнитная цепь характеризуется величиной магнитной индукции — В
, которая зависит от напряженности поля и магнитной проницаемости материала. Именно поэтому сердечники электромагнитов делают из железа, обладающего высокой магнитной проницаемостью. При конструировании электромагнитов весьма желательно получить большой силовой поток. Добиться этого можно, если уменьшить магнитное сопротивление. Для этого надо выбрать магнитопровод с наименьшей длиной пути силовых линий и с наибольшим поперечным сечением, а в качестве материала — железоматериал с большой магнитной проницаемостью. Другой путь увеличения силового потока путем увеличения ампервитков не является приемлемым, так как в целях экономии проволоки и питания следует стремиться к уменьшению ампервитков. Обычно расчеты электромагнитов делаются по специальным графикам. В целях упрощения в расчетах мы будем также пользоваться некоторыми выводами из графиков. Предположим, требуется определить ам-первитки и силовой поток замкнутого железного магнитопровода, изображенного на рисунке 4,а и сделанного из железа самого низкого качества. Рассматривая график намагничивания железа, нетрудно убедиться, что наиболее выгодной является магнитная индукция в пределах от
10 000
до
14 000
силовых линий на 1 см2, что соответствует от
2
до
7
ампервиткам на 1 см. Для намотки катушек с наименьшим числом витков и более экономичных в смысле питания для расчетов надо принимать именно эту величину (
10 000
силовых линий на 1 см2 при 2 ампервитках на 1 см длины). В этом случае расчет может быть произведен следующим образом. Так, при длине магнитопровода
Z=/1-)-/2
, равной
20 см-f-10 см = 30 см
, потребуется
2×30=60
ампервитков. Для двухполюсного магнита этот, результат следует удвоить. Следовательно,
Р=24,8 кг ^ 25 кг
. При определении подъемной силы необходимо помнить, что она зависит не только от длины магнитопровода, но, и от площади соприкосновения якоря и сердечника. Поэтому якорь должен точно прилегать к полюсным наконечникам, иначе даже малейшие воздушные прослойки вызовут сильное уменьшение подъемной силы. Далее производится расчет катушки электромагнита. В нашем примере подъемная сила в
25 кг
обеспечивается
60
ампервитками. Рассмотрим, какими средствами можно получить произведение
N-J—60
ампервиткам. Очевидно, этого можно добиться либо путем использования большого тока при малом количестве витков катушки, например 2 а и 30 витков, либо путем увеличения числа витков катушки при уменьшении, тока, например 0,25 а и 240 витков. Таким обра-1 зом, чтобы электромагнит имел подъемную силу в 25 кг, на его сердечник можно намотать, и 30 витков и 240 витков, но при этом изменить величину питающего тока. Конечно, можно выбрать и другое соотношение. Однако изменение величины тока в больших пределах не всегда возможно, так как оно обязательно потребует изменения диаметра применяемой проволоки. Так, при кратковременной работе (несколько минут) для проводов диаметром до 1. мм допустимую плотность тока, при которой не происходит сильного перегревания провода, можно принять равной
5 A/мм2
. В нашем примере проволока должна быть следующего сечения: для тока в
2A — 0,4 мм2
, а для тока в
0,25A — 0,05 мм2
. Каким же из этих проводов следует производить обмотку? С одной стороны, выбор диаметра провода может определяться имеющимся у руководителя ассортиментом проволоки, с другой — возможностями источников питания как по току, так и по напряжению. Действительно, две катушки, одна из которых изготовлена из толстой проволоки в 0,7 мм и с небольшим числом витков — 30, а другая — из проволоки в 0,2 мм и числом витков 240, будут иметь резко различное сопротивление. Зная диаметр проволоки и ее длину, можно легко определить сопротивление. Длина проволоки равна произведению общего числа витков на длину одного из них (среднюю):
l=Nxlt
где
lt
— длина одного витка, равная
3,14 x Д
. В нашем примере Д = 2 см, и 1г x 6,3 см. Следовательно, для первой катушки длина провода будет 30 x 6,3 = 190 см, а для второй — 240 X 6,3 = 1 512 см. Сопротивления обмоток будут также различными. Пользуясь законом Ома, нетрудно вычислить необходимое напряжение. Так, для создания в обмотках тока в 2A необходимое напряжение равно 0,2B, а для тока в 0,25A — 2,5B. Таким образом, для питания первой катушки достаточно одного элемента или аккумулятора, причем для понижения напряжения приходится включать реостат; для питания второй катушки необходимо взять два элемента, соединяя их последовательно. Ясно, что во втором случае имеется меньше потерь электроэнергии и обмотка получается более выгодной. Анализ полученных результатов позволяет сделать еще такой вывод: диаметр проволоки подбирается так, чтобы питание катушки можно было производить только от одного элемента (или аккумулятора) без каких-либо реостатов, где энергия тратится непроизвольно. Нетрудно заметить, что при диаметре проволоки приблизительно 0,4 мм и силе тока около 0,4 а нужное напряжение для питания катушки составит 1,3-г-1,4 в,-то-есть как раз напряжение одного элемента. Таков элементарный расчет электромагнитов.
Расчет магнитных цепей переменного тока
5.6.1. Особенности расчета магнитных цепей переменного тока.
Магнитные цепи переменного тока обладают следующими особенностями. Ток в катушке электромагнита зависит в основном от индуктивного сопротивления, которое, в свою очередь, определяется величиной воздушного зазора. Магнитное сопротивление цепи зависит от потерь в стали и наличия короткозамкнутых обмоток, расположенных на магнитопроводе.
Магнитопровод обычно выполняется шихтованным (с целью уменьшения потерь на вихревые токи) прямоугольного поперечного сечения, что ведет к увеличению средней длины витка обмотки и расходу меди.
Рассмотрим влияние этих особенностей на расчет магнитной цепи переменного тока.
5.6.2. Учет влияния потерь в стали.
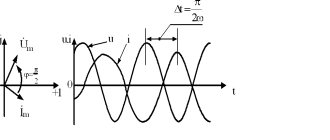
Векторная диаграмма магнитной цепи при переменном токе имеет вид, показанный на рис. 62 и подобна векторной диаграмме трансформатора в режиме холостого хода. На диаграмме вектор МДС кА-тушки
(Iw)
сдвинут относительно вектора по-
тока Фм
на угол . МДС катушки может быть разложена на две составляющие:
(Iw)а
– активную составляющую, совпадающую по фазе с магнитным потоком и расходуемую на проведение потока через все участки магнитной цепи;
(Iw)р
– реактивную составляющую, сдвину-
Рис. 62. Векторная диаграмма
тую по отношению к магнитному потоку
на угол 90 градусов. Реактивная составляющая МДС расходуется на компенсацию воздействия потерь в стали от перемагничивания и вихревых токов.
По аналогии с электрическими цепями можно записать:
– активная составляющая магнитного сопротивления магнитной цепи;
– реактивная составляющая магнитного сопротивления магнитной цепи;
– полное магнитное сопротивление.
Таким образом, влияние перемагничивания магнитопровода и возникающих в нем вихревых токов может быть учтено введением в схему замещения магнитной цепи индуктивных магнитных сопротивлений . Следовательно, участки магнитопровода магнитной цепи переменного тока характеризуются полным комплексным магнитным сопротивлением
или . (157)
Значения магнитных сопротивлений можно определить следующим образом:
, (158)
здесь γ
– плотность стали;
рст
– удельные потери в стали;
V
– объем стали участка магнитной цепи;
f
– частота сети;
Bm
– амплитуда магнитной индукции;
S
– площадь сечения стального участка м.ц.;
Фm
– амплитуда магнитного потока.
, (159)
здесь Uм
– магнитное напряжение на рассматриваемом участке м.ц.;
l
– средняя длина магнитной линии на участке м.ц.;
Hм
– напряженность магнитного поля на участке м.ц.; – магнитная проницаемость стали на участке м.ц..
Значения Hм
,
Bm
и определяются по кривой намагничивания, снятой на переменном токе. Тогда, активное сопротивление магнитопровода будет равно
. (160)
Участки магнитной цепи в виде воздушных промежутков создают только активное магнитное сопротивление, так как на этих участках нет потерь на перемагничивание и вихревые токи
. (161)
5.6.3. Учет влияния короткозамкнутой обмотки.
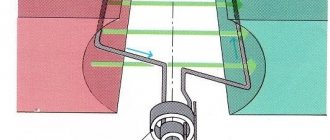
Влияние короткозамкнутой обмотки рассмотрим на примере электромагнита переменного тока П-образного типа, с короткозамкнутой обмоткой, охватывающей все сечение сердечника (рис. 63).
Потоками рассеяния пренебрегаем. Составим уравнение равновесия МДС по второму закону Кирхгофа в комплексной форме
, (162)
где
r2
и
x2
– активное и индуктивное сопротивления короткозамкнутой обмотки.
ЭДС, наводимая в к.з. обмотке
Рис. 63. Электромагнит
. (163)
переменного тока
Подставим (165) в
I2
и сделаем преобразова-
ния
. (164)
Значение I2
подставим в уравнение равновесия (164) и решаем относительно
I1w1
. (165)
Введем обозначения
; . (166)
Таким образом, короткозамкнутая обмотка учитывается при расчете магнитной цепи с помощью двух магнитных сопротивлений –
активного
Rм2
и индуктивного
Xм2
. Тогда уравнение магнитной цепи с короткозамкнутой обмоткой описывается законом Ома
. (167)
В магнитных цепях переменного тока короткозамкнутая обмотка выполняется в виде одного витка – экрана, охватывающего часть полюса в воздушном зазоре. Экран служит для уменьшения вибрации якоря. В связи с этим, индуктивное сопротивление экрана мало (x2 << r2
), так
как w2
= 1 и им можно пренебречь (
x2
= 0). Тогда,
Rм2
= 0 . (168)
В схеме замещения экран учитывается введением индуктивного сопротивления Xэ
.
5.6.4. Зависимость тока и потока от воздушного зазора.
Рассмотрим простейшую магнитную цепь переменного тока (рис. 63) без учета сопротивления стали (
Rмст= 0
), потерь в ней (
Pст= 0
), потоков рассеяния ( ) и короткозамкнутых экранов (
Xэ= 0
).
Напряжение сети, приложенное к катушке, уравновешивается активным и реактивным падением напряжения
, (169) где U
и
I
принимаются в действующих значениях.
. (170)
Отсюда следует, что индуктивное сопротивление обмотки будет равно
, (171)
т. е., оно обратно пропорционально воздушному зазору.
Для шунтовой обмотки, т. е. обмотки, подключаемой параллельно зажимам источника питания, активное сопротивление значительно меньше реактивного (R
<< ). Поэтому в первом приближении можно пренебречь активным сопротивлением (
R
= 0) и тогда
U = IX
. (172)
Но так как , то тогда получим – амплитудное значение потока.
Таким образом, при сделанных допущениях (R
= 0 и
Pст
= 0), поток, связанный с катушкой, не зависит от рабочего зазора и является величиной постоянной, а при
U = IX
следует
, (173)
то-есть, с ростом воздушного зазора индуктивное сопротивление обмотки уменьшается, а ток в ней увеличивается.
Однако, принятое допущение справедливо лишь в ограниченном диапазоне изменений воздушных зазоров. Так, из графиков (рис. 64) видно, что в диапазоне зазоров активное сопротивление R
соизмеримо с индуктивным сопротивлением
X
и даже
Рис. 64. Зависимости
больше его. Поэтому, с учетом активного сопро-
R и X от δ
тивления обмотки магнитный поток будет равен
, (174)
С ростом рабочего воздушного зазора ток в обмотке возрастает, а поток в магнитной цепи будет падать так же, как и в магнитной цепи постоянного тока. Но в магнитной цепи постоянного тока уменьшение потока происходит в результате роста магнитного сопротивления воздушного зазора, а в магнитной цепи переменного тока еще и в результате увеличения падения напряжения на активном сопротивлении обмотки. Если учитывать поток рассеяния Фs
, то при увеличении зазора ток в обмотке будет нарастать не пропорционально, как это
Рис. 65. К расчету магнитной цепи
следует из формулы (173), а значи-
переменного тока
тельно медленее.
Таким образом, активное сопротивление и магнитный поток рассеяния сдерживают рост тока в катушке электромагнита.
5.6.1. Особенности расчета магнитных цепей переменного тока.
Магнитные цепи переменного тока обладают следующими особенностями. Ток в катушке электромагнита зависит в основном от индуктивного сопротивления, которое, в свою очередь, определяется величиной воздушного зазора. Магнитное сопротивление цепи зависит от потерь в стали и наличия короткозамкнутых обмоток, расположенных на магнитопроводе.
Магнитопровод обычно выполняется шихтованным (с целью уменьшения потерь на вихревые токи) прямоугольного поперечного сечения, что ведет к увеличению средней длины витка обмотки и расходу меди.
Рассмотрим влияние этих особенностей на расчет магнитной цепи переменного тока.
5.6.2. Учет влияния потерь в стали.
Векторная диаграмма магнитной цепи при переменном токе имеет вид, показанный на рис. 62 и подобна векторной диаграмме трансформатора в режиме холостого хода. На диаграмме вектор МДС кА-тушки
(Iw)
сдвинут относительно вектора по-
тока Фм
на угол . МДС катушки может быть разложена на две составляющие:
(Iw)а
– активную составляющую, совпадающую по фазе с магнитным потоком и расходуемую на проведение потока через все участки магнитной цепи;
(Iw)р
– реактивную составляющую, сдвину-
Рис. 62. Векторная диаграмма
тую по отношению к магнитному потоку
на угол 90 градусов. Реактивная составляющая МДС расходуется на компенсацию воздействия потерь в стали от перемагничивания и вихревых токов.
По аналогии с электрическими цепями можно записать:
– активная составляющая магнитного сопротивления магнитной цепи;
– реактивная составляющая магнитного сопротивления магнитной цепи;
– полное магнитное сопротивление.
Таким образом, влияние перемагничивания магнитопровода и возникающих в нем вихревых токов может быть учтено введением в схему замещения магнитной цепи индуктивных магнитных сопротивлений . Следовательно, участки магнитопровода магнитной цепи переменного тока характеризуются полным комплексным магнитным сопротивлением
или . (157)
Значения магнитных сопротивлений можно определить следующим образом:
, (158)
здесь γ
– плотность стали;
рст
– удельные потери в стали;
V
– объем стали участка магнитной цепи;
f
– частота сети;
Bm
– амплитуда магнитной индукции;
S
– площадь сечения стального участка м.ц.;
Фm
– амплитуда магнитного потока.
, (159)
здесь Uм
– магнитное напряжение на рассматриваемом участке м.ц.;
l
– средняя длина магнитной линии на участке м.ц.;
Hм
– напряженность магнитного поля на участке м.ц.; – магнитная проницаемость стали на участке м.ц..
Значения Hм
,
Bm
и определяются по кривой намагничивания, снятой на переменном токе. Тогда, активное сопротивление магнитопровода будет равно
. (160)
Участки магнитной цепи в виде воздушных промежутков создают только активное магнитное сопротивление, так как на этих участках нет потерь на перемагничивание и вихревые токи
. (161)
5.6.3. Учет влияния короткозамкнутой обмотки.
Влияние короткозамкнутой обмотки рассмотрим на примере электромагнита переменного тока П-образного типа, с короткозамкнутой обмоткой, охватывающей все сечение сердечника (рис. 63).
Потоками рассеяния пренебрегаем. Составим уравнение равновесия МДС по второму закону Кирхгофа в комплексной форме
, (162)
где
r2
и
x2
– активное и индуктивное сопротивления короткозамкнутой обмотки.
ЭДС, наводимая в к.з. обмотке
Рис. 63. Электромагнит
. (163)
переменного тока
Подставим (165) в
I2
и сделаем преобразова-
ния
. (164)
Значение I2
подставим в уравнение равновесия (164) и решаем относительно
I1w1
. (165)
Введем обозначения
; . (166)
Таким образом, короткозамкнутая обмотка учитывается при расчете магнитной цепи с помощью двух магнитных сопротивлений –
активного
Rм2
и индуктивного
Xм2
. Тогда уравнение магнитной цепи с короткозамкнутой обмоткой описывается законом Ома
. (167)
В магнитных цепях переменного тока короткозамкнутая обмотка выполняется в виде одного витка – экрана, охватывающего часть полюса в воздушном зазоре. Экран служит для уменьшения вибрации якоря. В связи с этим, индуктивное сопротивление экрана мало (x2 << r2
), так
как w2
= 1 и им можно пренебречь (
x2
= 0). Тогда,
Rм2
= 0 . (168)
В схеме замещения экран учитывается введением индуктивного сопротивления Xэ
.
5.6.4. Зависимость тока и потока от воздушного зазора.
Рассмотрим простейшую магнитную цепь переменного тока (рис. 63) без учета сопротивления стали (
Rмст= 0
), потерь в ней (
Pст= 0
), потоков рассеяния ( ) и короткозамкнутых экранов (
Xэ= 0
).
Напряжение сети, приложенное к катушке, уравновешивается активным и реактивным падением напряжения
, (169) где U
и
I
принимаются в действующих значениях.
. (170)
Отсюда следует, что индуктивное сопротивление обмотки будет равно
, (171)
т. е., оно обратно пропорционально воздушному зазору.
Для шунтовой обмотки, т. е. обмотки, подключаемой параллельно зажимам источника питания, активное сопротивление значительно меньше реактивного (R
<< ). Поэтому в первом приближении можно пренебречь активным сопротивлением (
R
= 0) и тогда
U = IX
. (172)
Но так как , то тогда получим – амплитудное значение потока.
Таким образом, при сделанных допущениях (R
= 0 и
Pст
= 0), поток, связанный с катушкой, не зависит от рабочего зазора и является величиной постоянной, а при
U = IX
следует
, (173)
то-есть, с ростом воздушного зазора индуктивное сопротивление обмотки уменьшается, а ток в ней увеличивается.
Однако, принятое допущение справедливо лишь в ограниченном диапазоне изменений воздушных зазоров. Так, из графиков (рис. 64) видно, что в диапазоне зазоров активное сопротивление R
соизмеримо с индуктивным сопротивлением
X
и даже
Рис. 64. Зависимости
больше его. Поэтому, с учетом активного сопро-
R и X от δ
тивления обмотки магнитный поток будет равен
, (174)
С ростом рабочего воздушного зазора ток в обмотке возрастает, а поток в магнитной цепи будет падать так же, как и в магнитной цепи постоянного тока. Но в магнитной цепи постоянного тока уменьшение потока происходит в результате роста магнитного сопротивления воздушного зазора, а в магнитной цепи переменного тока еще и в результате увеличения падения напряжения на активном сопротивлении обмотки. Если учитывать поток рассеяния Фs
, то при увеличении зазора ток в обмотке будет нарастать не пропорционально, как это
Рис. 65. К расчету магнитной цепи
следует из формулы (173), а значи-
переменного тока
тельно медленее.
Таким образом, активное сопротивление и магнитный поток рассеяния сдерживают рост тока в катушке электромагнита.
Войти на сайт
Железный сердечник является одной частью магнитопровода, а другой частью, с помощью которой замыкается путь магнитных силовых линий, служит якорь.
Магнитная цепь характеризуется величиной магнитной индукции — В, которая зависит от напряженности поля и магнитной проницаемости материала. Именно поэтому сердечники электромагнитов делают из железа, обладающего высокой магнитной проницаемостью.
В свою очередь, от магнитной индукции зависит силовой поток, обозначаемый в формулах буквой Ф.
Ф = B х S = магнитная индукция х площадь поперечного сечения магнитопровода.
При конструировании электромагнитов весьма желательно получить большой силовой поток. Добиться этого можно, если уменьшить магнитное сопротивление. Для этого надо выбрать магнитопровод с наименьшей длиной пути силовых линий и с наибольшим поперечным сечением, а в качестве материала — железоматериал с большой магнитной проницаемостью.
Другой путь увеличения силового потока путем увеличения ампервитков не является приемлемым, так как в целях экономии проволоки и питания следует стремиться к уменьшению ампервитков.
Обычно расчеты электромагнитов делаются по специальным графикам. В целях упрощения в расчетах мы будем также пользоваться некоторыми выводами из графиков. Предположим, требуется определить ампервитки и силовой поток замкнутого железного магнитопровода, изображенного на рисунке и сделанного из железа самого низкого качества.
Рассматривая график намагничивания железа, нетрудно убедиться, что наиболее выгодной является магнитная индукция в пределах от 10 000 до 14 000 силовых линий на 1 см2, что соответствует от 2 до 7 ампервиткам на 1 см. Для намотки катушек с наименьшим числом витков и более экономичных в смысле питания для расчетов надо принимать именно эту величину (10 000 силовых линий на 1 см2 при 2 ампервитках на 1 см длины). В этом случае расчет может быть произведен следующим образом. Так, при длине магнитопровода l = l1 + l2, равной 20 см + 10 см = 30 см, потребуется 2×30=60 ампервитков.
Если диаметр сердечника примем равным 2 см, то его площадь будет равна S = (3,14 х d2) / 4 = 3,14 см2. Отсюда возбуждаемый магнитный поток будет равен: Ф = B х S = 10000 х 3,14 = 31400 силовых линий.
Можно приблизительно вычислить подъемную силу электромагнита (P).
P = B2х S / (25 х 1000000) = 12,4 кг.
Для двухполюсного магнита этот, результат следует удвоить. Следовательно, Р=24,8 кг, или приблизительно 25 кг.
При определении подъемной силы необходимо помнить, что она зависит не только от длины магнитопровода, но, и от площади соприкосновения якоря и сердечника. Поэтому якорь должен точно прилегать к полюсным наконечникам, иначе даже малейшие воздушные прослойки вызовут сильное уменьшение подъемной силы.
Далее производится расчет катушки электромагнита. В нашем примере подъемная сила в 25 кг обеспечивается 60 ампервитками. Рассмотрим, какими средствами можно получить произведение N х J — 60 ампервиткам.
Очевидно, этого можно добиться либо путем использования большого тока при малом количестве витков катушки, например 2 а и 30 витков, либо путем увеличения числа витков катушки при уменьшении, тока, например 0,25 А и 240 витков.
Таким образом, чтобы электромагнит имел подъемную силу в 25 кг, на его сердечник можно намотать, и 30 витков и 240 витков, но при этом изменить величину питающего тока. Конечно, можно выбрать и другое соотношение.
Однако изменение величины тока в больших пределах не всегда возможно, так как оно обязательно потребует изменения диаметра применяемой проволоки. Так, при кратковременной работе (несколько минут) для проводов диаметром до 1 мм допустимую плотность тока, при которой не происходит сильного перегревания провода, можно принять равной 5 A/мм2. В нашем примере проволока должна быть следующего сечения: для тока в 2A — 0,4 мм2, а для тока в 0,25A — 0,05 мм2.
Каким же из этих проводов следует производить обмотку?
С одной стороны, выбор диаметра провода может определяться имеющимся у руководителя ассортиментом проволоки, с другой — возможностями источников питания как по току, так и по напряжению. Действительно, две катушки, одна из которых изготовлена из толстой проволоки в 0,7 мм и с небольшим числом витков — 30, а другая — из проволоки в 0,2 мм и числом витков 240, будут иметь резко различное сопротивление.
Зная диаметр проволоки и ее длину, можно легко определить сопротивление. Длина проволоки равна произведению общего числа витков на длину одного из них (среднюю): l=N x lt где lt — длина одного витка, равная 3,14 x d.
В нашем примере d = 2 см, и lt 6,3 см. Следовательно, для первой катушки длина провода будет 30 x 6,3 = 190 см, а для второй — 240 X 6,3 = 1512 см. Сопротивления обмоток будут также различными.
Пользуясь законом Ома, нетрудно вычислить необходимое напряжение. Так, для создания в обмотках тока в 2A необходимое напряжение равно 0,2B, а для тока в 0,25A — 2,5B.
Таким образом, для питания первой катушки достаточно одного элемента или аккумулятора, причем для понижения напряжения приходится включать реостат. Для питания второй катушки необходимо взять два элемента, соединяя их последовательно. Ясно, что во втором случае имеется меньше потерь электроэнергии и обмотка получается более выгодной.
Анализ полученных результатов позволяет сделать еще такой вывод: диаметр проволоки подбирается так, чтобы питание катушки можно было производить только от одного элемента (или аккумулятора) без каких-либо реостатов, где энергия тратится непроизвольно. Нетрудно заметить, что при диаметре проволоки приблизительно 0,4 мм и силе тока около 0,4 А нужное напряжение для питания катушки составит 1,3 — 1,4 В, то есть как раз напряжение одного элемента.
Таков элементарный расчет электромагнитов.
Источник: Техническое творчество. Издательство ЦК ВЛКСМ “Молодая гвардия”. М., 1955 г.
Саму книгу в формате DjVu Вы можете скачать по этой ссылке: https://narod.ru/disk/21046539000/creation.zip.html (30 мб)