Всем доброго времени суток! В прошлой статье я рассказал о воздействии переменного напряжения на элементы цепи (сопротивление, индуктивность и ёмкость) и воздействие этих элементов на напряжение, ток и мощность. В данной статье я расскажу о последовательном и параллельном соединении элементов цепи и воздействии на такие цепи переменного напряжения и тока.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Последовательное соединение элементов цепи при переменном напряжении
Начнём с последовательного соединения сопротивления R, индуктивности L и ёмкости C и рассмотрим воздействие на неё переменного напряжения с частотой ω.
Последовательное соединение элементов цепи.
В данной цепи входное переменное напряжение U в соответствии со вторым законом Кирхгофа будет равно алгебраической сумме переменных напряжений на отдельных элементах
где UR, UL, UC – напряжение на элементах цепи, сопротивлении R, индуктивности L и ёмкости С, соответственно,
Im – амплитудное значение переменного тока.
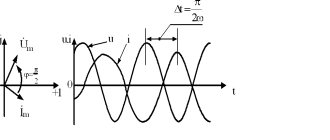
Графическое изображение напряжений и токов на последовательно соединённых элементах цепи представлено ниже
Напряжения и токи при последовательном соединении.
Итоговое выражение является тригонометрической формой записи второго закона Кирхгофа для мгновенных напряжений и его можно переписать в виде
где R – активное сопротивление,
Х – реактивное сопротивление.
Значение активного сопротивления R всегда только положительно, а реактивное сопротивление Х может принимать, как положительное значение Х > 0, тогда оно имеет индуктивный характер, так и отрицательное значение X < 0, в этом случае реактивное сопротивление имеет ёмкостный характер.
В случае же нулевого значения реактивного сопротивления, имеет место резонанс напряжений
В этом случае сопротивление цепи представлено только активной нагрузкой R, а следовательно сдвиг фаз между напряжением и током будет нулевым.
При расчётах нас интересует не столько ток и напряжение на отдельных элементах, сколько ток и напряжение всей цепи. Для этого продолжим преобразовывать напряжение
где Z – полное сопротивление цепи,
ψ – разность фаз между напряжением и током.
Таким образом, амплитудное значение напряжения Um и амплитудное значение тока Im связаны между собой следующим соотношением
где Um – амплитудное значение переменного напряжения,
Im – амплитудное значение переменного тока,
Z – полное сопротивление цепи.
Электрические цепи переменного тока
Переменный ток получил гораздо большее распространение в промышленности и в быту, чем постоянный, так как упрощается конструкция электродвигателей, а синхронные генераторы могут быть выполнены на значительно большие мощности и более высокие напряжения, чем генераторы постоянного тока. Переменный ток позволяет легко изменять величину напряжения с помощью трансформаторов, что необходимо при передаче электроэнергии на большие расстояния.
Амплитудой переменного тока называется наибольшее значение, положительное или отрицательное, принимаемое переменным током.
Периодом называется время, в течение которого происходит полное колебание тока в проводнике.
Фазой называется угол
или , стоящий под знаком синуса. Фаза характеризует состояние переменного тока с течением времени. При t=0 фаза называется начальной.
Периодический режим:
. К такому режиму может быть отнесен и синусоидальный: — амплитуда; — начальная фаза; — угловая скорость вращения ротора генератора.
При f=50Гц T= 1/f=0,02 с,
314рад/с. График синусоидальной функции называется волновой диаграммой.
Расчет цепей переменного тока с использованием мгновенных значений тока, напряжения и ЭДС требует громоздкой вычислительной работы. Поэтому изменяющиеся непрерывно во времени токи, напряжения и ЭДС заменяют эквивалентными во времени величинами.
При расчете электрических цепей синусоидальную функцию выражают по формуле Эйлера через экспоненциальные функции:
— поворотный множитель; — комплексная амплитуда напряжения; — сопряженная комплексная амплитуда напряжения.
Таким образом, синусоидальное напряжение можно представить на комплексной плоскости вращающимся вектором. Тогда амплитудное значение напряжения
будет представлять собой модуль или длину вектора напряжения.
Параллельное соединение элементов цепи при переменном напряжении
Теперь рассмотрим параллельное соединение элементов цепи (сопротивления, индуктивности и ёмкости) и прохождение по ним переменного тока.
Параллельно соединение элементов цепи.
Подадим на вход такой цепи переменное напряжение U, тогда электрический ток в цепи I, в соответствии с первым законом Кирхгофа, будет равняться алгебраической суммы токов проходящей через элементы цепи
IR, IL, IC – токи в элементах цепи, сопротивлении R, индуктивности L и ёмкости С, соответственно,
Um – амплитудное значение переменного тока.
Графическое изображение напряжений и токов в параллельно соединённых элементах цепи представлено ниже
Напряжение и токи при параллельном соединении.
Аналогично второму закону Кирхгофа, для первого закона также существует тригонометрическая форма записи, которая соответствует получившемуся выражению. Выполним ещё одно преобразование данного выражения
где g – активная проводимость, b – реактивная проводимость.
Как видно из формулы, реактивная проводимость может быть положительной b > 0, тогда она имеет индуктивный характер, а может быть отрицательной b < 0, тогда реактивная проводимость имеет ёмкостный характер. А активная проводимость может быть только положительной.
Отдельный случай представляет собой реактивная проводимость равная нулю, то есть в этом случае проводимость индуктивности и ёмкости одинаковы
Такой случай называется резонансом токов, в этом случае общая проводимость будет определяться только активной проводимостью, а сдвиг фаз между напряжением и током в цепи будет нулевым.
Определим зависимость между напряжением и силой тока в параллельной цепи
где y – полная проводимость,
ψ – разность фаз между напряжением и током в цепи.
Тогда зависимость между напряжением и током в цепи с параллельно соединёнными элементами будет иметь вид
где Um – амплитудное значение переменного напряжения,
Im – амплитудное значение переменного тока,
y – полная проводимость цепи.
Электромагнитные процессы, протекающие в электротехнических устройствах, как правило, достаточно сложны. Однако во многих случаях, их основные характеристики можно описать с помощью таких интегральных понятий, как: напряжение, ток, электродвижущая сила (ЭДС). При таком подходе совокупность электротехнических устройств, состоящую из соответствующим образом соединенных источников и приемников электрической энергии, предназначенных для генерации, передачи, распределения и преобразования электрической энергии и (или) информации, рассматривают как электрическую цепь
. Электрическая цепь состоит из отдельных частей (объектов), выполняющих определенные функции и называемых
элементами цепи
. Основными элементами цепи являются источники и приемники электрической энергии (сигналов). Электротехнические устройства, производящие электрическую энергию, называются
генераторами
или
источниками электрической энергии
, а устройства, потребляющие ее –
приемниками
(потребителями) электрической энергии.
У каждого элемента цепи можно выделить определенное число зажимов (полюсов
), с помощью которых он соединяется с другими элементами. Различают
двух
–и
многополюсные
элементы. Двухполюсники имеют два зажима. К ним относятся источники энергии (за исключением управляемых и многофазных), резисторы, катушки индуктивности, конденсаторы. Многополюсные элементы – это, например, триоды, трансформаторы, усилители и т.д.
Все элементы электрической цепи условно можно разделить на активные
и
пассивные
. Активным называется элемент, содержащий в своей структуре источник электрической энергии. К пассивным относятся элементы, в которых рассеивается (резисторы) или накапливается (катушка индуктивности и конденсаторы) энергия. К основным характеристикам элементов цепи относятся их вольт-амперные, вебер-амперные и кулон-вольтные характеристики, описываемые дифференциальными или (и) алгебраическими уравнениями. Если элементы описываются линейными дифференциальными или алгебраическими уравнениями, то они называются
линейными
, в противном случае они относятся к классу
нелинейных
. Строго говоря, все элементы являются нелинейными. Возможность рассмотрения их как линейных, что существенно упрощает математическое описание и анализ процессов, определяется границами изменения характеризующих их переменных и их частот. Коэффициенты, связывающие переменные, их производные и интегралы в этих уравнениях, называются
параметрами
элемента.
Если параметры элемента не являются функциями пространственных координат, определяющих его геометрические размеры, то он называется элементом с сосредоточенными параметрами
. Если элемент описывается уравнениями, в которые входят пространственные переменные, то он относится к классу
элементов с распределенными параметрами
. Классическим примером последних является линия передачи электроэнергии (длинная линия).
Цепи, содержащие только линейные элементы, называются линейными. Наличие в схеме хотя бы одного нелинейного элемента относит ее к классу нелинейных.
Рассмотрим пассивные элементы цепи, их основные характеристики и параметры.
1. Резистивный элемент (резистор)
Условное графическое изображение резистора приведено на рис. 1,а. Резистор – это пассивный элемент, характеризующийся резистивным сопротивлением. Последнее определяется геометрическими размерами тела и свойствами материала: удельным сопротивлением r (Ом´ м) или обратной величиной – удельной проводимостью (См/м).
В простейшем случае проводника длиной и сечением S его сопротивление определяется выражением
.
В общем случае определение сопротивления связано с расчетом поля в проводящей среде, разделяющей два электрода.
Основной характеристикой резистивного элемента является зависимость (или ), называемая вольт-амперной характеристикой (ВАХ). Если зависимость представляет собой прямую линию, проходящую через начало координат (см.рис. 1,б), то резистор называется линейным и описывается соотношением
или
,
где — проводимость. При этом R=const.
Нелинейный резистивный элемент, ВАХ которого нелинейна (рис. 1,б), как будет показано в блоке лекций, посвященных нелинейным цепям, характеризуется несколькими параметрами. В частности безынерционному резистору ставятся в соответствие статическое и дифференциальное сопротивления.
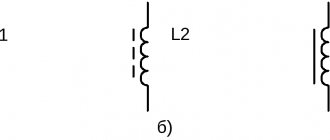
2. Индуктивный элемент (катушка индуктивности)
Условное графическое изображение катушки индуктивности приведено на рис. 2,а. Катушка – это пассивный элемент, характеризующийся индуктивностью. Для расчета индуктивности катушки необходимо рассчитать созданное ею магнитное поле.
Индуктивность определяется отношением потокосцепления к току, протекающему по виткам катушки,
.
В свою очередь потокосцепление равно сумме произведений потока, пронизывающего витки, на число этих витков , где .
Основной характеристикой катушки индуктивности является зависимость , называемая вебер-амперной характеристикой. Для линейных катушек индуктивности зависимость представляет собой прямую линию, проходящую через начало координат (см. рис. 2,б); при этом
.
Нелинейные свойства катушки индуктивности (см. кривую на рис. 2,б) определяет наличие у нее сердечника из ферромагнитного материала, для которого зависимость магнитной индукции от напряженности поля нелинейна. Без учета явления магнитного гистерезиса нелинейная катушка характеризуется статической и дифференциальной индуктивностями.
3. Емкостный элемент (конденсатор)
Условное графическое изображение конденсатора приведено на рис. 3,а.
Конденсатор – это пассивный элемент, характеризующийся емкостью. Для расчета последней необходимо рассчитать электрическое поле в конденсаторе. Емкость определяется отношением заряда q на обкладках конденсатора к напряжению u между ними
и зависит от геометрии обкладок и свойств диэлектрика, находящегося между ними. Большинство диэлектриков, используемых на практике, линейны, т.е. у них относительная диэлектрическая проницаемость =const. В этом случае зависимость представляет собой прямую линию, проходящую через начало координат, (см. рис. 3,б) и
.
У нелинейных диэлектриков (сегнетоэлектриков) диэлектрическая проницаемость является функцией напряженности поля, что обусловливает нелинейность зависимости (рис. 3,б). В этом случае без учета явления электрического гистерезиса нелинейный конденсатор характеризуется статической и дифференциальной емкостями.
Схемы замещения источников электрической энергии
Свойства источника электрической энергии описываются ВАХ , называемой внешней характеристикой источника.
Далее в этом разделе для упрощения анализа и математического описания будут рассматриваться источники постоянного напряжения (тока). Однако все полученные при этом закономерности, понятия и эквивалентные схемы в полной мере распространяются на источники переменного тока. ВАХ источника может быть определена экспериментально на основе схемы, представленной на рис. 4,а. Здесь вольтметр V измеряет напряжение на зажимах 1-2 источника И, а амперметр А – потребляемый от него ток I, величина которого может изменяться с помощью переменного нагрузочного резистора (реостата) RН.
В общем случае ВАХ источника является нелинейной (кривая 1 на рис. 4,б). Она имеет две характерные точки, которые соответствуют:
а – режиму холостого хода
;
б – режиму короткого замыкания
.
Для большинства источников режим короткого замыкания (иногда холостого хода) является недопустимым. Токи и напряжения источника обычно могут изменяться в определенных пределах, ограниченных сверху значениями, соответствующими номинальному режиму
(режиму, при котором изготовитель гарантирует наилучшие условия его эксплуатации в отношении экономичности и долговечности срока службы). Это позволяет в ряде случаев для упрощения расчетов аппроксимировать нелинейную ВАХ на рабочем участке m-n (см. рис. 4,б) прямой, положение которой определяется рабочими интервалами изменения напряжения и тока. Следует отметить, что многие источники (гальванические элементы, аккумуляторы) имеют линейные ВАХ.
Прямая 2 на рис. 4,б описывается линейным уравнением
| , | (1) |
где — напряжение на зажимах источника при отключенной нагрузке (разомкнутом ключе К в схеме на рис. 4,а); — внутреннее сопротивление источника
.
Уравнение (1) позволяет составить последовательную схему замещения
источника (см. рис. 5,а). На этой схеме символом Е обозначен элемент, называемый
идеальным источником ЭДС
. Напряжение на зажимах этого элемента не зависит от тока источника, следовательно, ему соответствует ВАХ на рис. 5,б. На основании (1) у такого источника . Отметим, что направления ЭДС и напряжения на зажимах источника противоположны.
Если ВАХ источника линейна, то для определения параметров его схемы замещения
необходимо провести замеры напряжения и тока для двух любых режимов его работы.
Существует также параллельная схема замещения источника. Для ее описания разделим левую и правую части соотношения (1) на . В результате получим
или
| , | (2) |
где ; — внутренняя проводимость источника
.
Уравнению (2) соответствует схема замещения источника на рис. 6,а.
На этой схеме символом J обозначен элемент, называемый идеальным источником тока
. Ток в ветви с этим элементом равен и не зависит от напряжения на зажимах источника, следовательно, ему соответствует ВАХ на рис. 6,б. На этом основании с учетом (2) у такого источника , т.е. его внутреннее сопротивление .
Отметим, что в расчетном плане при выполнении условия последовательная и параллельная схемы замещения источника являются эквивалентными. Однако в энергетическом отношении они различны, поскольку в режиме холостого хода для последовательной схемы замещения мощность равна нулю, а для параллельной – нет.
Кроме отмеченных режимов функционирования источника, на практике важное значение имеет согласованный режим
работы, при котором нагрузкой RН от источника потребляется максимальная мощность
| , | (3) |
Условие такого режима
| , | (4) |
В заключение отметим, что в соответствии с ВАХ на рис. 5,б и 6,б идеальные источники ЭДС и тока являются источниками бесконечно большой мощности.
Литература
- Основы
теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с. - Бессонов Л.А
. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с. - Теоретические
основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.1. К.М.Поливанов. Линейные электрические цепи с сосредоточенными постоянными. –М.: Энергия, 1972. –240 с. - Каплянский А.Е.
и др. Теоретические основы электротехники. Изд. 2-е. Учеб. пособие для электротехнических и энергетических специальностей вузов. –М.: Высш. шк., 1972. –448 с.
Контрольные вопросы и задачи
- Может ли внешняя характеристик источника проходить через начало координат?
- Какой режим (холостой ход или короткое замыкание) является аварийным для источника тока?
- В чем заключаются эквивалентность и различие последовательной и параллельной схем замещения источника?
- Определить индуктивность L и энергию магнитного поля WМкатушки, если при токе в ней I=20А потокосцепление y =2 Вб.
Ответ: L=0,1 Гн; WМ=40 Дж. - Определить емкость С и энергию электрического поля WЭконденсатора, если при напряжении на его обкладках U=400 В заряд конденсатора q=0,2´ 10-3 Кл.
Ответ: С=0,5 мкФ; WЭ=0,04 Дж. - У генератора постоянного тока при токе в нагрузке I1=50Анапряжение на зажимах U1=210 В,а притоке, равном I2=100А, оно снижается до U2=190 В.
- Определить параметры последовательной схемы замещения источника и ток короткого замыкания.
Ответ: - Вывести соотношения (3) и (4) и определить максимальную мощность, отдаваемую нагрузке, по условиям предыдущей задачи.
Ответ: