Анализ линейных электрических цепей (стр. 3 )

В чем разница между сопротивлением и проводимостью?

Сопротивление, по определению, является мерой «трения», которое компонент представляет для прохождения через него тока. Сопротивление обозначается заглавной буквой «R» и измеряется в единицах «Ом». Однако мы также можем думать об этом электрическом свойстве с обратной ему точки зрения: насколько легко току течь через компонент, а не насколько трудно.

Если сопротивление – это термин, которое мы используем для обозначения меры того, насколько трудно току течь, то хорошим термином, чтобы выразить, насколько легко ток течет, будет проводимость. Математически проводимость – это величина, обратная сопротивлению:

\[проводимость = \frac{1}{сопротивление}\]

Чем больше сопротивление, тем меньше проводимость; и наоборот.

Это должно быть интуитивно понятно, потому что сопротивление и проводимость – противоположные способы обозначения одного и того же важного электрического свойства.

Если сравнивать сопротивления двух компонентов и обнаружится, что компонент «A» имеет сопротивление вдвое меньше сопротивления компонента «B», то в качестве альтернативы мы могли бы выразить это соотношение, сказав, что компонент «A» в два раза более проводящий, чем компонент «B». Если компонент «A» имеет сопротивление, равное только одной трети от сопротивления компонента «B», то мы можем сказать, что он в три раза более проводящий, чем компонент «B», и так далее.

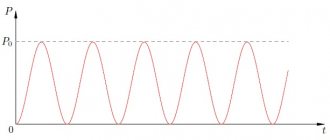
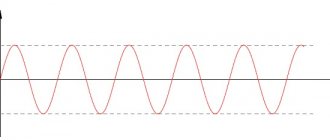
Токи в цепи

Характер изменения этих зависимостей очевиден и его можно обосновать, используя зависимости, рассмотренные в пунктах 1-3. Графики приведены на рис. 14.

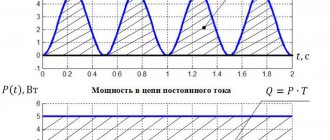
Мощности
S
,
P
,
Qв цепи.

Активная мощность на всей цепи

;

реактивная мощность изменяется линейно от С

зависимость полной мощности от С

подобна зависимости , поскольку

Графики, указанных зависимостей приведены на рис. 15.

Участок цепи, в котором возникает резонанс токов, называют параллельным резонансным контуром. При резонансе токов в соответствии с (12) становится минимально возможной величиной. Как следует из (5), уменьшая активное сопротивление катушки индуктивности и увеличивая её , можно значительно уменьшить и проводимость . Т.е. значительно увеличить сопротивление контура при резонансе токов. Если питать этот контур от источника синусоидального сигнала, ток которого слабо зависит от сопротивления контура (так называемая модель источника тока), то при резонансе токов напряжение на ветвях может в несколько десятков или сотен раз превышать это напряжение при других режимах работы. Это позволяет использовать такие контуры для качественного выделения сигнала определенной (резонансной) частоты во время поиска нужной радиостанции при приеме ее сигнала. Поэтому резонанс токов находит широкое применение в радиотехнике, телевидении, технике проводной электросвязи, измерительной технике, в специальных источниках вторичного электропитания устройств промышленной электроники.

Единица измерения проводимости

В продолжение этой идеи были придуманы символ и единица измерения проводимости. Символ представляет собой заглавную букву «G», а единицей измерения был mho, что означает «ohm» (ом), написанное в обратном порядке (вы думали, что у электронщиков нет чувства юмора?).

Несмотря на свою уместность, единицы измерения mho в последующие годы были заменены единицей Сименс (сокращенно «См», или, в англоязычной литературе, «S»). Это решение об изменении названий единиц измерения напоминает изменение единицы измерения температуры в градусах стоградусной шкалы (degrees centigrade – от латинских слов «centum», т.е. «сто», и «gradus») на градусы Цельсия (degrees Celsius) или изменение единицы измерения частоты c.p.s. (циклов в секунду) в герцы. Если вы ищете здесь какой-то шаблон переименования, то Сименс, Цельсий и Герц – это фамилии известных ученых, имена которых, к сожалению, о природе единиц говорят нам меньше, чем их первоначальные обозначения.

Возвращаясь к нашему примеру с параллельной схемой, мы должны быть в состоянии увидеть, что несколько путей (ветвей) для тока уменьшают общее сопротивление всей цепи, поскольку ток может легче проходить через всю цепь из нескольких ветвей, чем через любую из них отдельно. Что касается сопротивления, дополнительные ветви приводят к меньшему общему значению (ток встречает меньшее сопротивление). Однако с точки зрения проводимости дополнительные ветви приводят к большему общему значению (ток протекает с большей проводимостью).

Цепь с идеальным емкостным элементом

Учебный материал: лекция

На любом участке цепи переменного тока одновременно осуществляются необратимые процессы преобразования электрической энергии в другие виды и проявляется действие переменного электромагнитного поля.

При решении большинства электротехнических задач вводят допущения, которые позволяют раздельно учитывать каждое из явлений и упрощают задачу расчета электрических цепей переменного тока.

Цепь с идеальным резистивным элементом.

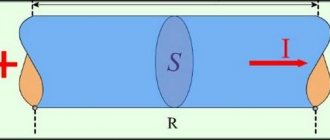
Рассмотрим, например, процессы, происходящие в обыкновенной лампе накаливания, включенной в сеть переменного тока. Между отдельными витками нити накаливания существует электрическая емкость, и нить обладает определенной индуктивностью, но они незначительны. Поэтому считают, что С=0 и L=0. В этом случае при анализе электрической цепи лампу называют идеальным резистивным элементом цепи с сопротивлением R.

Величина сопротивления переменному току больше, чем сопротивлению постоянному току, за счет неравномерного распределения тока в проводе (поверхностный эффект). Поэтому в отличие от сопротивления постоянному току сопротивление в цепи переменного тока называют активным сопротивлением

. Активное сопротивление измеряется
в омах
.

Если напряжение u = Um sinωt),подключить к сопротивлению R, то через него протекает ток

Это показывает, что напряжение на сопротивлении и ток, протекающий через него, совпадают по фазе: .

Напряжение, совпадающее по фазе с током, называют активным напряжением и обозначают Ua.

Цепь с идеальным индуктивным элементом.

Примером идеального индуктивного элемента может служить индуктивная катушка. Электрическая энергия, выделяемая в катушке за счет нагрева провода обмотки, как правило, невелика, как и межвитковая емкость, и во многих практических случаях ими можно пренебречь (R=0, C=0). При принятых допущениях индуктивную катушку называют идеальным индуктивным элементом цепи или L-элементом.

Параметром идеального индуктивного элемента является индуктивность L

, а энергетические процессы в нем определяются только явлениями, происходящими в магнитном поле.

Индуктивность — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность, краем которой является этот контур. На электрических схемах используют условные графические обозначения катушек индуктивностей, примеры которых приведены на рисунке.

Условные графические обозначения индуктивностей:

а – обозначение катушки индуктивности; б – с магнитодиэлектрическим сердечником;

в – с ферромагнитным сердечником

При прохождении электрического тока по катушке, ток создаст переменный магнитный поток Ф. Силовые линии этого потока, пересекая витки катушки, будут индуктировать в ней э.д.с. самоиндукции. По закону электромагнитной индукции

eL=

Так как в цепи, куда включена индуктивность L, отсутствует активное сопротивление (рассматривается идеальная катушка индуктивности), то по второму закону Кирхгофа u+eL=0, т. е. u = -eL Следовательно, напряжение источника всегда равно по величине и противо-положно по направлению э. д. с. самоиндукции.

Если в формулу подставить значение тока и продифференцировать, то получим:

Обозначим величину ωL· равной амплитуде напряжения Um. Тогда по закону Ома

Величину называют индуктивным сопротивлением

, измеряют в Омах и обозначают

Так как , то начальную фазу напряжения можно представить как φ u= φ i+ 90 и, следовательно,

Выведенное соотношение показывает, что если в катушке протекает синусоидальный ток, то напряжение также имеет синусоидальный характер, но при этом оно опережает ток на четверть периода (90°).

Цепь с идеальным емкостным элементом

Конденсатор – элемент электрической цепи, предназначенный для использования его ёмкости. В конденсаторе накапливается энергия электрического поля. Свойство элемента запасать электрический заряд характеризует ёмкость (С)

. Этот параметр является коэффициентом пропорциональности между зарядом
q (Кл)
и прикладываемым напряжением
u (В).
q = C·u,

При изменении напряжения на конденсаторе изменяется заряд и возникает электрический ток

Идеализированный конденсатор обладает только ёмкостью С (R=0, L=0).

Рассмотрим электрические процессы в цепи с идеальным ёмкостным элементом. Пусть напряжение источника изменяется по закону u = Um·sinωt, (φu = 0).

В цепи возникает ток

Из полученного выражения видно, что начальная фаза тока φi = . Угол сдвига фаз между напряжением и током составляет

Следовательно, синусоида напряжения на емкости отстаёт от синусоиды тока на угол 90°. На практике, если в электрической цепи напряжение отстаёт по фазе от тока, говорят об ёмкостном характере нагрузки.

Амплитуда тока будет равна Im = ω·C·Um= .

Величину называют ёмкостным сопротивлением

конденсатора и измеряют в Омах

Xc=1/ ω•C =1/2πfC.

Итак, в цепях переменного тока выделяют следующие виды сопротивлений:

— активное

(активным называют сопротивление резистора). Единицей измерения сопротивления является Ом. Сопротивление резистора не зависит от частоты сети.

— реактивное (

индуктивное XL и емкостное ХС). Единицей измерения индуктивного и емкостного сопротивления также является Ом. Величина индуктивного сопротивления линейно зависит от частоты. А величина ёмкостного сопротивления обратнопропорциональна частоте сети. В цепях со смешанным соединением нагрузки (активной, индуктивной, ёмкостной) реактивным сопротивлением цепи называют величину

X = XL — XC.

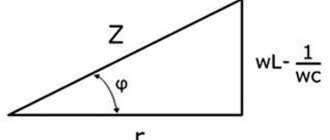
Для того, чтобы найти общее сопротивление электрической цепи со смешанным соединением нагрузки используют понятие полного сопротивления цепи, которое определяется как

Домашнее задание:

1. Ответить на вопросы:

· Объясните физический смысл активного сопротивления проводника переменному току по сравнению с сопротивлением проводника постоянному току?

· — Что такое индуктивность катушки? От чего она зависит?

· — Что понимается под действующим значением переменного синусоидального тока? Как его рассчитать через амплитудное значение тока?

· — Опишите физические явления, наблюдаемые в резисторе в цепи переменного синусоидального тока?

· — Запишите математическую связь между мгновенным напряжением, мгновенным током и активным сопротивлением?

· — Запишите математические выражения мгновенного напряжения и тока на активном сопротивлении, приняв начальную фазу напряжения φ=45°.

· — Что понимается под углом сдвига фаз? Чему он равен на участке цепи с резистором? индуктивностью? ёмкостью?

· — Как рассчитать индуктивное сопротивление идеальной катушки?

· — Запишите математическое выражение мгновенного напряжения на индуктивном сопротивлении, приняв начальную фазу тока φ=45°.

· — Объясните физический смысл ёмкостного сопротивления. Как рассчитать ёмкостное сопротивление идеального конденсатора?

· — Чему равен угол сдвига фаз в ёмкости?

· — Что понимается под термином реактивное сопротивление? Как его определить?

· — Как в сети переменного тока определяется полное сопротивление?

2. Скан копию или фото домашнего задания , вопросы отправляем в личные сообщения преподавателю

Учебник

А.С.Касаткин, М.В.Немцов. – 8-е изд., испр.-М. : Издательский , 2003.-544 с.

Общая проводимость параллельной цепи

Общая проводимость параллельной цепи больше, чем проводимость любой из отдельных ветвей, потому что параллельные резисторы «проводят» вместе лучше, чем по отдельности:

Рисунок 2 – Полная проводимость параллельной цепи

Чтобы быть более точным, полная проводимость в параллельной цепи равна сумме отдельных проводимостей:

\[G_{общ} = G_1 + G_2 + G_3 + G_4\]

Если мы знаем, что проводимость – это не что иное, как математическая величина, обратная (1/x) сопротивлению, мы можем перевести каждый член приведенной выше формулы в сопротивление, подставив величину, обратную каждой соответствующей проводимости:

\[\frac{1}{R_{общ}} = \frac{1}{R_{1}} + \frac{1}{R_{2}} + \frac{1}{R_{3}} + \frac{1}{R_{4}}\]

Решая приведенное выше уравнение для полного сопротивления (вместо значения, обратного общему сопротивлению), мы получим следующую формулу:

\[R_{общ} = \frac{1}{\frac{1}{R_{1}} + \frac{1}{R_{2}} + \frac{1}{R_{3}} + \frac{1}{R_{4}}}\]

Итак, мы, наконец, пришли к нашей загадочной формуле сопротивления! Проводимость (G) редко используется в качестве практического параметра, поэтому при анализе параллельных цепей часто используется приведенная выше формула.

Основные величины и методы расчета электрической цепи переменного синусоидального тока

Определение 1
Переменный электрический ток — это электрический ток, который изменяется по направлению и величине в течении времени (в некоторых случаях изменяется только его величина).

В быту для электроснабжения используется переменный синусоидальный ток.

Определение 2

Синусоидальный электрический ток — это электрический ток, который изменяется во времени по синусоидальному закону.

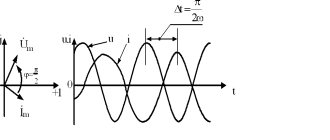
Графически синусоидальный закон изображен на рисунке ниже.

Рисунок 1. График. Автор24 — интернет-биржа студенческих работ

Ты эксперт в этой предметной области? Предлагаем стать автором Справочника Условия работы

$I = Imsin * ((2пt / T) + ф) = Imsin * (wt + ф)$

где: Im – максимальное значение амплитуды электрического тока; T – время, за которое совершается одно полное колебание (период); f – количество колебаний за одну секунду(частота); w – угловая частота; п = 3,14; — ф — начальная фаза

Частота колебаний рассчитывается по следующей формуле:

$f = 1 / Т$

Угловую частоту рассчитывают следующим образом:

$w = 2п * f = 2п / Т$

Любая синусоидальная функция определяется следующими величинами, которые являются основными характеристиками переменного синусоидального тока: