Вектор магнитной индукции. Сила Ампера и сила Лоренца

Источники магнитного поля

Приведенный выше эксперимент наглядно демонстрирует, как любой человек может определить направление силовых линий магнитного поля Земли. Стрелка прибора покажет направления на южный и северный полюс. Продольная ось этого индикатора будет совпадать с вектором (В).

Электромагнитное поле проводника

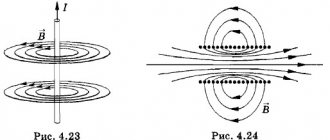
Если аналогичный опыт выполнить около проводника с током, по движению стрелки можно определить круговое расположение силовых линий. Они образуют замкнутые кольца, перпендикулярные осевой линии кабеля.

Электромагнитная индукция

Достаточно сильное поле образует индукционная катушка. Практический пример – соленоид реле или запорного устройства. При включении такой узел втягивает внутрь металлический сердечник.

Что такое электромагнитная индукция

Вектор магнитной индукции: формула

Это явление сопровождается возникновением поля в определенной среде, тока – в проводящем материале или поляризации отдельных предметов. Электромагнитная индукция зависит от изменения магнитных параметров со временем или соответствующего перемещения функциональных компонентов.

Установлена точная дата данного открытия – 29.08.1831 г. Известен автор – М. Фарадей. Ученый выявил пропорциональную зависимость ЭДС в замкнутом контуре от скорости, с которой изменяется магнитный поток.

Основные формулы для вычисления вектора МИ

Вектор магнитной индукции, формула которого B = Fm/I*∆L, можно находить, применяя другие математические вычисления.

Закон Био-Савара-Лапласа

Формула ЭДС индукции

Описывает правила нахождения B→ магнитного поля, которое создаёт постоянный электроток. Это экспериментально установленная закономерность. Био и Савар в 1820 году выявили её на практике, Лапласу удалось сформулировать. Этот закон является основополагающим в магнитостатике. При практическом опыте рассматривался неподвижный провод с малым сечением, через который пропускали электроток. Для изучения выбирался малый участок провода, который характеризовался вектором dl. Его модуль соответствовал длине рассматриваемого участка, а направление совпадало с направлением тока.

Интересно. Лаплас Пьер Симон предложил считать током даже движение одного электрона и на этом утверждении, с помощью данного закона, доказал возможность определения МП продвигающегося точечного заряда.

Согласно этому физическому правилу, каждый сегмент dl проводника, по которому протекает электрический ток I, образовывает в пространстве вокруг себя на промежутке r и под углом α магнитное поле dB:

dB = µ0 *I*dl*sin α /4*π*r2,

где:

• dB – магнитная индукция, Тл;
• µ0 = 4 π*10-7 – магнитная постоянная, Гн/м;
• I – сила тока, А;
• dl – отрезок проводника, м;
• r – расстояние до точки нахождения магнитной индукции, м;
• α – угол, образованный r и вектором dl.

Важно! Согласно закону Био-Савара-Лапласа, суммируя векторы магнитных полей отдельных секторов, можно определить МП нужного тока. Оно будет равно векторной сумме.

Закон Био-Савара-Лапласа

Существуют формулы, описывающие этот закон для отдельных случаев МП:

• поля прямого перемещения электронов;
• поля кругового движения заряженных частиц.

Формула для МП первого типа имеет вид:

В = µ* µ0*2*I/4*π*r.

Для кругового движения она выглядит так:

В = µ*µ0*I/4*π*r.

В этих формулах µ – это магнитная проницаемость среды (относительная).

Рассматриваемый закон вытекает из уравнений Максвелла. Максвелл вывел два уравнения для МП, случай, где электрическое поле постоянно, как раз рассматривают Био и Савар.

Принцип суперпозиции

Для МП существует принцип, согласно которому общий вектор магнитной индукции в определённой точке равен векторной сумме всех векторов МИ, созданных разными токами в данной точке:

B→= B1→+ B2→+ B3→… + Bn→

Принцип суперпозиции

Теорема о циркуляции

Изначально в 1826 году Андре Ампер сформулировал данную теорему. Он разобрал случай с постоянными электрическими полями, его теорема применима к магнитостатике. Теорема гласит: циркуляция МП постоянного электричества по любому контуру соразмерна сумме сил всех токов, которые пронизывают этот контур.

Стоит знать! Тридцать пять лет спустя Д. Максвелл обобщил это утверждение, проведя параллели с гидродинамикой.

Другое название теоремы – закон Ампера, описывающий циркуляцию МП.

Математически теорема записывается следующим образом.

Математическая формула теоремы о циркуляции

где:

• B→– вектор магнитной индукции;
• j→ – плотность движения электронов.

Это интегральная форма записи теоремы. Здесь в левой части интегрируют по некоторому замкнутому контуру, в правой части – по натянутой поверхности на полученный контур.

Будет интересно➡ Что собой представляет контактор, его особенности и схемы подключения

Магнитный поток

Одна из физических величин, характеризующих уровень МП, пересекающего любую поверхность, – магнитный поток. Обозначается буквой φ и имеет единицу измерения вебер (Вб). Эта единица характерна для системы СИ. В СГС магнитный поток измеряется в максвеллах (Мкс):

108 Мкс = 1 Вб.

Магнитный поток φ определяет величину МП, пронизывающую определённую поверхность. Поток φ зависит от угла, под которым поле пронизывает поверхность, и силы поля.

Формула для расчёта имеет вид:

φ = |B*S| = B*S*cosα,

где:

• В – скалярная величина градиента магнитной индукции;
• S – площадь пересекаемой поверхности;
• α – угол, образованный потоком Ф и перпендикуляром к поверхности (нормалью).

Внимание! Поток Ф будет наибольшим, когда B→ совпадёт с нормалью по направлению (угол α = 00). Аналогично Ф = 0, когда он проходит параллельно нормали (угол α = 900).

Магнитный поток

Вектор магнитной индукции, или магнитная индукция, указывает направление поля. Применяя простые методы: правило буравчика, свободно ориентирующуюся магнитную стрелку или контур с током в магнитном поле, можно определить направление действия этого поля.

Законы Ленца и Фарадея

Явление электромагнитной индукции

Закон Фарадея показывает математическое соотношение важнейших параметров этого явления:

E = — dФ/dt,

где:

• Е – ЭДС;
• Ф – поток, образованный проникающим через ограниченный контур вектором магнитной индукции;
• t – время.

В этом выражении «-» перед основной частью обозначает правило, сформулированное Э. Ленцем. Этот российский ученый установил, что ток в рассматриваемом контуре создает направленность поля, противоположную силовой компоненте магнитного потока.

Для практического применения удобнее выразить отмеченные выше закономерности следующим образом:

Е = -N*(dФв/dt).

В этом примере представлена индукционная катушка, помещенная в магнитное (переменное) поле. Дополнительные компоненты:

• N – количество витков соленоида;
• Фв – поток через единичный виток.

В дифференциальном представлении этот закон описывают интегралом по произвольной поверхности от вектора магнитной индукции, который пронизывает область с определенными границами. Подобная форма позволяет учесть только изменения поля. Магнитным потоком называют совокупность линий, которые проходят через определенную площадку. Для упрощения расчетов полагают, что поле является однородным.

Правило правой руки для магнитных и электрических сил

Формула ЭДС индукции

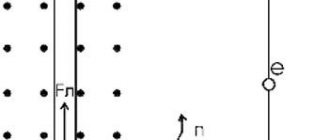
Если проводник перемещается в постоянном магнитном поле, в нем образуется движение заряженных частиц. Для уточнения основных параметров явления не нужны расчеты и эксперименты. Достаточно запомнить простую технологию, изображенную на следующем рисунке.

При таком расположении постоянного магнита перемещают проводник снизу вверх в сторону, куда указывает поднятый большой палец. Ладонь поворачивают в сторону северного полюса. Четыре сомкнутых пальца покажут направление движения индукционного тока.

Специальные правила

Рассмотрим варианты главного правила буравчика для частных случаев. Применение таких правил часто упрощает процесс вычислений.

Для векторного произведения

Расположите векторы так, чтобы их начальные точки совпадали. Для этой ситуации правило буравчика звучит так:

Если один из векторов сомножителей вращать кратчайшим способом до совпадения направлений со вторым вектором, то буравчик, вращающийся подобным образом, будет завинчиваться в сторону, куда указывает векторное произведение.

По циферблату часов

При расположении векторов способом совпадения их начальных точек можно определить направление вектора-произведения с помощью часовой стрелки. Для этого необходимо мысленно двигать кратчайшим путём один из векторов-сомножителей в сторону другого вектора. Тогда, если смотреть со стороны вращения этого вектора по часовой стрелке, то аксиальный вектор будет направлен вглубь циферблата.

Векторного произведения

Это правило (в переписанном виде) отличается от предыдущих. У него есть два варианта звучания. Первая формулировка правила правой руки читайте:

1. Если вы изобразите вектора таким образом, чтобы их начальные координаты совместились при наложении;
2. Начнёте вращать первый BC (вектор-сомножитель) самым коротким способом ко второму ВС;
3. А также расположите все пальцы правой руки (за исключением большого) так, чтобы они демонстрировали сторону, в направлении коей происходило вращение, словно вы сжимаете в руке цилиндр;
4. Тогда ваш большой палец укажет направление ВП (вектора-произведения).

Вторая формулировка часто именуется «пистолетом» и звучит так:

1. Если вы изобразите вектора таким образом, чтобы их начальные координаты совместились при наложении;
2. Большой палец расположите по направлению первого BC;
3. Указательный — по направлению второго ВС
4. Тогда и только тогда ваш средний палец укажет примерное направление ВП.

Советуем к прочтению: Транзисторы и диоды: как работают полупроводники

Это мнемоническое правило довольно несложно запоминать как ФБР — на английском эта аббревиатура FBI:

1. F — сила, которая протекает параллельно среднему пальцу;
2. B — вектор магнитной индукции, направленный по указательному
3. I — ток, протекающий по большому.

Кроме того, как я уже упоминала ранее, его ещё называют «пистолетом»: несложно заметить, что ваши пальцы при его выполнении будут расположены в виде пистолета.

На этом наше изучение правила правой руки подошло к концу, и мы обратимся к третьему (и кратчайшему) разделу статьи — правилу левой руки (ПЛР).

Для базисов

Это правило будет работать и для базисов почти аналогично. В правом базисе при вращении штопора, направленного по одному из векторов, по наиболее короткому пути ко второму вектору закручивание инструмента укажет направление третьего вектора. Для простоты запоминания представляют настенные часы: две вектора — это стрелки, а третий направлен к или от наблюдателя (выбор будет определять ориентацию всего базиса, то есть будет он правым или левым).

Сведения о линиях магнитной индукции

Из приведенных данных понятна силовая природа поля, созданного переменным током или перемещением проводника. Векторное выражение используют для точного выражения воздействий на индикаторный элемент. В начале публикации таким компонентом была стрелка компаса. Далее показана возможность применения проводящей рамки с током.

Линии индукции магнитного поля применяют для наглядного изображения данного явления. Если в любой точке такой кривой нарисовать вектор (В) по касательной, он укажет направление воздействия. Размером в масштабе показывают определенную силу.

Элементарной проверкой геометрических параметров можно установить уникальность каждого вектора. Они, как и линии силового поля, не пересекаются. Ниже представлены способы для уточнения распределения энергетических потоков в проводнике и окружающем пространстве.

Для варианта с прямолинейным проводником правую руку сжимают, как показано на первом рисунке. Большой палец направляют в сторону движения тока. Сжатые пальцы покажут направление силовых линий. Вторая часть картинки демонстрирует определение параметров поля при пропускании тока через кольцевую рамку – «правило буравчика». Вращение этого инструмента аналогично направлению тока.

К сведению. Если соленоид достаточно большой по длине, поле в большей части рабочего объема будет однородным. Допустимо считать, что линии магнитного поля в этом случае расположены параллельно.

Что связано с левой рукой

Не путайте буравчика и правило левой руки, оно нужно для определения действующей на проводник силы. Выпрямленная ладонь левой руки располагается вдоль проводника. Пальцы показывают в сторону протекания тока I. Через раскрытую ладонь проходят линии поля. Большой палец совпадает с вектором силы – в этом и заключается смысл правила левой руки. Эта сила называется силой Ампера.

Можно это правило применить к отдельной заряженной частице и определить направление 2-х сил:

1. Лоренца.
2. Ампера.

Представьте, что положительно заряженная частица двигается в магнитном поле. Линии вектора магнитной индукции перпендикулярны направлению её движения. Нужно поставить раскрытую левую ладонь пальцами в сторону движения заряда, вектор B должен пронизывать ладонь, тогда большой палец укажет направление вектора Fа. Если частица отрицательная – пальцы смотрят против хода заряда.

Если какой-то момент вам был непонятен, на видео наглядно рассматривается, как пользоваться правилом левой руки:

Важно знать! Если у вас есть тело и на него действует сила, которая стремится его повернуть, вращайте винт в эту сторону, и вы определите, куда направлен момент силы. Если вести речь об угловой скорости, то здесь дело обстоит так: при вращении штопора в одном направлении с вращением тела, завинчиваться он будет в направлении угловой скорости.

Правило левой руки: что можно определить, воспользовавшись им

Не стоит путать правила левой руки и буравчика – они предназначены для совершенно разных целей. При помощи левой руки можно определить две силы, вернее, их направление. Это:

• сила Лоренца;
• сила Ампера.

Попробуем разобраться, как это работает.

Применение для силы Ампера

Силы Ампера, в чём оно заключается

Первое правило левой руки связано с силой Андре-Мари Ампера, кою французский учёный открыл в тысяча восемьсот двадцатом году — сразу после закона Ампера. Принцип его работы следующий:

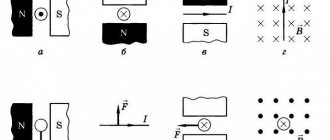
1. Поместите свою левую ладонь так, чтобы в её внутреннюю сторону перпендикулярно ей входили линии индукции магнитного поля;
2. Все пальцы, за исключением большого, направьте по электротоку
3. В таком случае, ваш левый большой палец, который должен образовать прямой угол с остальными, покажет направление силы, которая будет действовать со стороны магнитного поля на проводник с током — то есть силы Ампера.

Однако это только один вариант ПЛР.

Сила Лоренца применение и формула

Действие электромагнитных полей порождает возникновение точечной заряженной частицы, на который воздействуют силы электрического и магнитного характера. В скомбинированном виде они получили наименование силы Лоренца.

Таким образом, сила Лоренца воздействует на любую частицу с зарядом, падающую с определенной быстротой в магнетическом поле. Степень влияния связана с электрическим зарядом частицы (q), показателем магнитной индукции (В) и быстротой падения частицы (V).

На основании полученных данных голландским ученым Хендриком Лоренцем была выведена формула: FL = |q|x V x B x sinα. Все условные обозначения приведены на рисунке.

В практической деятельности сила Лоренца получила применение в следующих областях:

• Кинескопы – электронно-лучевые или телевизионные трубки. В этих устройствах электроны, летящие в направлении экрана, отклоняются магнитным полем, которое создают специальные катушки.
• Масс-спектрографы. Определяют массы заряженных частиц, путем разделения их по удельным зарядам. Вакуумная камера помещается в магнитном поле. Заряженный частицы ускоряясь, двигаются по дуге и оставляют след на фотопластинке. Па радиусу траектории вначале определяется удельный заряд, на основании которого вычисляется и масса частицы.
• Циклотрон. Ускоряет заряженные частицы. Ускорение происходит под действием силы Лоренца, после чего траектория частиц сохраняется за счет магнитного поля. Прибор давно начали использовать в медицинских исследованиях с применением радионуклидных фармацевтических препаратов.
• Магнетрон. Электронная лампа высокой мощности для генерации микроволн, возникающих при взаимодействии электронного потока и магнитного поля. Используется с современных радиолокационных устройствах.

Советуем к прочтению: Для чего используется стабилитрон и как он работает

Изображение линий магнитной индукции

Чтобы наглядно изучить распределение поля в пространстве, уменьшают размеры измерительных элементов. Для эксперимента подойдут железные опилки, равномерно рассыпанные на поверхности картонного листа или другой электрически нейтральной плоскости.

Если поднести с обратной стороны магнит, металлические частицы, как миниатюрные стрелки компаса, распределяться вдоль силовых полос. По расстоянию между ними можно судить об энергетических параметрах поля в определенном месте. Аналогичным образом создают рисунок. Большая густота (около полюсов) свидетельствует об увеличенном значении индукции.

К сведению. Физическим разделением постоянного магнита на части не получится создать отдельные полюса. В этом – принципиальное отличие от электростатических зарядов определенной полярности, которые также создают силовое поле.

Представленные знания применяют для решения разных инженерных задач. В частности, пригодятся простые правила определения направления тока в проводнике и стороны, в которую перемещается сердечник соленоида.