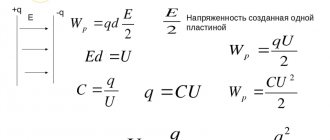В электрических цепях применяются различные способы соединения конденсаторов. Соединение конденсаторов может производиться: последовательно, параллельно и последовательно-параллельно (последнее иногда называют смешанное соединение конденсаторов). Существующие виды соединения конденсаторов показаны на рисунке 1.
Рисунок 1. Способы соединения конденсаторов.
Параллельное соединение конденсаторов.
Если группа конденсаторов включена в цепь таким образом, что к точкам включения непосредственно присоединены пластины всех конденсаторов, то такое соединение называется параллельным соединением конденсаторов (рисунок 2.).
Рисунок 2. Параллельное соединение конденсаторов.
При заряде группы конденсаторов, соединенных параллельно, между пластинами всех конденсаторов будет одна и та же разность потенциалов, так как все они заряжаются от одного и того же источника тока. Общее же количество электричества на всех конденсаторах будет равно сумме количеств электричества, помещающихся на каждом из конденсаторов, так как заряд каждого их конденсаторов происходит независимо от заряда других конденсаторов данной группы. Исходя из этого, всю систему параллельно соединенных конденсаторов можно рассматривать как один эквивалентный (равноценный) конденсатор. Тогда общая емкость конденсаторов при параллельном соединении равна сумме емкостей всех соединенных конденсаторов.
Обозначим суммарную емкость соединенных в батарею конденсаторов буквой Собщ, емкость первого конденсатора С1 емкость второго С2 и емкость третьего С3. Тогда для параллельного соединения конденсаторов будет справедлива следующая формула:
Последний знак + и многоточие указывают на то, что этой формулой можно пользоваться при четырех, пяти и вообще при любом числе конденсаторов.
Конденсаторы – задачи
В задачах с присутствием конденсаторов очень часто нужно уметь находить емкость последовательного и параллельного соединения емкостей. С параллельным соединением емкостей все просто: при параллельном соединении емкости складываются. Почему это так? Дело в том, что при параллельном соединении на всех конденсаторах одинаковое напряжение, а их заряды пропорциональны емкостям:
и т.д.
Общий заряд на конденсаторах:
Тогда емкость системы конденсаторов: .
С последовательным соединением все сложнее. Кстати, когда готовила эту статью, наткнулась на такой вот перл, который не могла не процитировать:
Заряды при последовательном соединении одинаковы на всех конденсаторах:
и т.д.
Тогда напряжение между крайними точками равно:
Емкость всей системы: , или
1. Разность потенциалов между точками А и В В. Емкость конденсаторов соответственно равна мкФ и мкФ. Определите заряды и и разности потенциалов и на обкладках первого и второго конденсаторов.
Задача 1
Определим общую емкость такого соединения: ,
мкФ (сразу считаем в микрофарадах, чтобы не расписывать степени десятки)
Тогда заряд равен:
мкКл.
Заряды при последовательном соединении на всех конденсаторах одинаковые, значит для первого:
, для второго .
Напряжения на конденсаторах:
В, В.
Ответ: 18 мкКл, 6 В, 3 В. 2. Определите емкость батареи конденсаторов, изображенной на рисунке. Емкость каждого конденсатора мкФ.
Задача 2
Емкости и , поскольку они соединены параллельно, необходимо сложить: мкФ. Тогда получим последовательное соединение трех одинаковых емкостей и , емкость которой вдвое больше. При последовательном соединении емкостей их эквивалентная емкость вычисляется по формуле: . Тогда получим: , мкФ.
Ответ: 286 нФ
3. Емкость батареи конденсаторов, образованной двумя последовательно включенными конденсаторами, 100 пФ, а заряд 20 нКл. Определите емкость второго конденсатора, а также разность потенциалов на обкладках каждого из них, если пФ.
Воспользуемся . Тогда (считаем в пикофарадах)
Отсюда , , пФ.
При последовательном соединении заряд на конденсаторах равный: нКл.
Напряжения также получатся одинаковыми:
В, В.
Ответ: В, нКл.
4. Наибольшая емкость конденсатора 60 мкФ. Какой заряд он накопит при подключении источника постоянного напряжения 60В?
Так как , то мКл.
Ответ: 0,36 мКл
5. При введении в пространство между пластинами воздушного конденсатора твердого диэлектрика напряжение на конденсаторе уменьшилось с 400 до 100 В. Какова диэлектрическая проницаемость диэлектрика?
Рассмотрим сначала конденсатор до введения диэлектрика: , . Заряд остался тем же при введении диэлектрика, а напряжение изменилось: .
Тогда , или
Емкость конденсатора, как известно, зависит от площади пластин и расстояния между ними, а также от диэлектрика:
В первом случае, без диэлектрика: , а во втором
Найдем и в этом случае отношение емкостей: , или
Ответ: Кл*Кл/Н*м*м
6. Площадь пластин конденсатора равна 520 см кв. На каком расстоянии нужно разместить пластины в воздухе, чтобы емкость конденсатора была равна 50 пФ?
Емкость конденсатора без диэлектрика:
Площадь нужно выразить в кв. метрах:
Электрическая постоянная .
Выразим из первого выражения нужную нам величину: м, или 9,2 мм.
Ответ: 9,2 мм
7. Конденсатору емкостью 20 мкФ сообщили заряд 5 мкКл. Какова энергия заряженного конденсатора?
Энергию электрического поля, накопленную конденсатором, можно вычислить по формуле:
– и в этой задаче как раз хорошо будет воспользоваться второй записью.
Тогда: мкДж
8. Расстояние между пластинами плоского конденсатора с диэлектриком из бумаги, пропитанной парафином, равно 2 мм, а напряжение 200 В. Найти плотность энергии поля.
Чтобы найти плотность энергии, нужно сначала определить энергию поля, а потом посчитать, в каком объеме она сосредоточена.
, с другой стороны, емкость , тогда . Объем пространства между пластинами конденсатора – это произведение площади пластин на расстояние между ними: . Тогда плотность энергии поля равна
Посмотрим в справочнике, какова диэлектрическая проницаемость бумаги с парафином, выразим расстояние между пластинами в метрах, и подставим цифры:
мДж
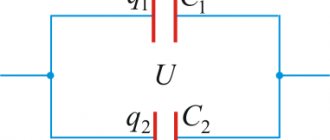
Последовательное соединение конденсаторов.
Если же соединение конденсаторов в батарею производится в виде цепочки и к точкам включения в цепь непосредственно присоединены пластины только первого и последнего конденсаторов, то такое соединение конденсаторов называется последовательным (рисунок 3).
Рисунок 2. Последовательное соединение конденсаторов.
При последовательном соединении все конденсаторы заряжаются одинаковым количеством электричества, так как непосредственно от источника тока заряжаются только крайние пластины (1 и 6), а остальные пластины (2, 3, 4 и 5) заряжаются через влияние. При этом заряд пластины 2 будет равен по величине и противоположен по знаку заряду пластины 1, заряд пластины 3 будет равен по величине и противоположен по знаку заряду пластины 2 и т. д.
Напряжения на различных конденсаторах будут, вообще говоря, различными, так как для заряда одним и тем же количеством электричества конденсаторов различной емкости всегда требуются различные напряжения. Чем меньше емкость конденсатора, тем большее напряжение необходимо для того, чтобы зарядить этот конденсатор требуемым количеством электричества, и наоборот.
Таким образом, при заряде группы конденсаторов, соединенных последовательно, на конденсаторах малой емкости напряжения будут больше, а на конденсаторах большой емкости — меньше.
Аналогично предыдущему случаю можно рассматривать всю группу конденсаторов, соединенных последовательно, как один эквивалентный конденсатор, между пластинами которого существует напряжение, равное сумме напряжений на всех конденсаторах группы, а заряд которого равен заряду любого из конденсаторов группы.
Возьмем самый маленький конденсатор в группе. На нем должно быть самое большое напряжение. Но напряжение на этом конденсаторе составляет только часть общего напряжения, существующего на всей группе конденсаторов. Напряжение на всей группе больше напряжения на конденсаторе, имеющем самую малую емкость. А отсюда непосредственно следует, что общая емкость группы конденсаторов, соединенных последовательно, меньше емкости самого малого конденсатора в группе.
Для вычисления общей емкости при последовательном соединении конденсаторов удобнее всего пользоваться следующей формулой:
Для частного случая двух последовательно соединенных конденсаторов формула для вычисления их общей емкости будет иметь вид:
Задачи на конденсаторы и электроемкость с решением
Если вы не знаете, как решать задачи с конденсаторами, сначала посмотрите теорию и вспомните про памятку по решению задач по физике и полезные формулы.
Задача №1 на электроемкость батареи конденсаторов
Условие
Плоский конденсатор емкостью 16 мкФ разрезают на 4 равные части вдоль плоскостей, перпендикулярных обкладкам. Полученные конденсаторы соединяют последовательно. Чему равна емкость батaреи конденсаторов?
Решение
Из условия следует, что площадь получившихся конденсаторов в 4 раза меньше, чем у исходного. Зная это, можно найти емкость каждого полученного конденсатора:
Соединяя 4 таких конденсатора последовательно, получаем:
Ответ: 1 мкФ.
Задача №2 на энергию плоского конденсатора
Условие
Плоский конденсатор заполнили диэлектриком с диэлектрической проницаемостью, равной 2. Энергия конденсатора без диэлектрика равна 20 мкДж. Чему равна энергия конденсатора после заполнения диэлектриком? Считать, что источник питания отключен от конденсатора.
Решение
Энергия конденсатора до заполнения диэлектриком равна:
После заполнения емкость конденсатора изменится:
Энергия конденсатора после заполнения:
Ответ: 40 мкФ.
Задача №3 на последовательное и параллельное соединение конденсаторов
Условие
На рисунке изображена батарея конденсаторов. Каждый конденсатор имеет емкость 1 мкФ. Найдите емкость батареи.
Решение
Как видим, часть конденсаторов соединена параллельно, а часть последовательно. Это типичный пример смешанного соединения конденсаторов. Алгоритм решения задач при смешанном соединении конденсаторов сводится к тому, чтобы упростить схему и свести все только к параллельному или последовательному соединению.
Конденсаторы 3 и 4 соединены параллельно. Складывая их емкость, получаем в итоге последовательное соединение четырех конденсаторов: 1, 2, 5 и 3-4. Для параллельного соединения:
Для последовательного соединения:
Ответ: 0,285 мкФ.
Задача №4 на пролет частицы в конденсаторе
Заряд конденсатора равен 0,3 нКл, а емкость – 10 пФ. Какую скорость приобретет электрон, пролетая в конденсаторе от одной пластины к другой. Начальная скорость электрона равна нулю.
Решение
По закону сохранения энергии, разность кинетических энергий электрона в начале и в конце пути будет равна работе поля по его перемещению. По условию, начальная кинетическая энергия электрона равна 0. Запишем:
С учетом этого, получим:
Ответ: 10^7 м/с.
Задача №5 на вычисление энергии электрического поля конденсатора
Условие
Конденсатор подключен к источнику постоянного напряжения U=1 кВ. Емкость конденсатора равна 5 пФ. Как изменяться заряд на обкладках конденсатора и его энергия, если расстояние между обкладками уменьшить в три раза.
Решение
Заряд конденсатора равен:
Изменение заряда будет равно:
Изменение энергии:
Ответ: 5 мкДж.
Последовательно-параллельное (смешанное) соединение конденсаторов
Последовательно-параллельным соединением конденсаторов называется цепь имеющая в своем составе участки, как с параллельным, так и с последовательным соединением конденсаторов.
На рисунке 4 приведен пример участка цепи со смешанным соединением конденсаторов.
Рисунок 4. Последовательно-параллельное соединение конденсаторов.
При расчете общей емкости такого участка цепи с последовательно-параллельным соединением конденсаторов этот участок разбивают на простейшие участки, состоящие только из групп с последовательным или параллельным соединением конденсаторов. Дальше алгоритм расчета имеет вид:
1. Определяют эквивалентную емкость участков с последовательным соединением конденсаторов.
2. Если эти участки содержат последовательно соединенные конденсаторы, то сначала вычисляют их емкость.
3. После расчета эквивалентных емкостей конденсаторов перерисовывают схему. Обычно получается цепь из последовательно соединенных эквивалентных конденсаторов.
4. Рассчитывают емкость полученной схемы.
Один из примеров расчета емкости при смешанном соединении конденсаторов приведен на рисунке 5.
Рисунок 5. Пример расчета последовательно-параллельного соединения конденсаторов.
Подробнее о расчетах соединения конденсаторов можно узнать в мультимедийном учебнике по основам электротехники и электроники:
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
- Электрическая емкость
- Емкость конденсатора
- Энергия поля конденсатора
- Виды конденсаторов
- Обозначение конденсаторов
Комментарии
#20 Владимир Николаевич 06.10.2019 09:48 На самом деле если подключить последовательно 3 конденсатора и каждый будет по 3 микро фарада, а напряжение в сети 100 вольт, то на выходе будет такая цифра 1 микрофорад и 300 вольт. Если параллельно, то ёмкость будет 9 микро фарад, а напряжение 100 вольт
Цитировать
#19 АлексейДу 19.09.2019 07:03 На практике, как правило на обоих концах не ровно по 110В, а примерно на одном конце 120В и на другом 100В, соответственно лучше заземлить и принять за ноль конец с меньшим напряжением. Определить конец с меньшим напряжем можно простой индикаторной отверткой с наконечником замыкающим большим пальцем, т.е. тот конец который будет светится с меньшей яркостью и нужно принять за ноль. Если разницу в свечении индикатора определить не сможете, то у вас идеальный генератор и можете заземлять любой конец розетки. Надеюсь я вам помог.
Цитировать
#18 АлексейДу 19.09.2019 07:02 Цитирую володя ж:
купил бензогенератор,а лампочка моргает! и стабилизатор не помогает. Может конденсаторы помогут проблеме? Спасибо
Если бензогенератор однофазный и переменного напряжения, то он работает по принципу двух полупериодов, т.е. на каждом конце (фаза и ноль) присутствует напряжение 110В, соответственно в сумме они дают 220В в розетке (с частотой 50 Гц, которую вы и наблюдаете как моргание лампочки). Что бы избавится от эффекта моргания, необходимо корпус генератора и один конец розетки присоединить к заземляющему контуру, тогда на заземленном конце напряжение станет равным нулю (0В), а на другом станет равным 220 (220В) чистой синусоиды и соответственно заземленный конец станет нулем, а незазаемленный фазой. Цитировать
#17 Денис25 09.10.2018 17:20 Цитирую володя ж:
купил бензогенератор,а лампочка моргает! и стабилизатор не помогает. Может конденсаторы помогут проблеме? Спасибо
Только онлайн типа инвертор поможет. Цитировать
#16 Трамвай 26.03.2018 14:42 отличная статья! Всё по полочкам, с наглядными примерами. Спасибо огромное)
Цитировать
#15 Тёма 10.01.2017 18:23 Чему будет равно общая (эквивалентная) электрическая ёмкость, если в электрической цепи соединить два конденсатора по 10Ф паралельно: 5Ф? 10Ф? 15Ф? 20Ф?
Цитировать
#14 иван 25.07.2016 16:19 При последовательно м соединении ёмкость конденсатора не растёт, и в данном случае последовательно 1+1+1=1 так как растёт напряжение подаваемое на эту сборку!!!!
Цитировать
#13 Administrator 30.09.2015 15:05 Цитирую Гуманоид:
Класс. сколько будет, если подключить параллельно три кондютера по 1мкф = 3мкф , а сколько будет, если подключить их последовательно 1/общ=1/1+1/1+1/1=1+1+1= = 3мкф лапша какая то
Интересная арифметика, я конечно извиняюсь, но где такому учат? Можно я посчитаю вспоминая математику третьего класса: 1/Собщ = 1/1+1/1+1/1=1+1+1= = 3 то есть 1/Собщ = 3 Теперь выразим Собщ = 1/3 = 0,3333333333 и т. д. По моему проще некуда. Думаю виновата не электротехника а математика. Вот придумали же делить… умножать… Так где же лапша…? А извиняюсь не прочитал имя Вы же ГУМАНОИД тогда все понятно! Цитировать
#12 Гуманоид 29.09.2015 22:44 Класс. сколько будет, если подключить параллельно три кондютера по 1мкф = 3мкф , а сколько будет, если подключить их последовательно 1/общ=1/1+1/1+1/1=1+1+1= = 3мкф лапша какая то
Цитировать
#11 Андей 14.12.2014 11:32 Нормальное объяснение
Цитировать
#10 Administrator 11.12.2014 19:59 Я понимаю генератор переменного тока? Если да то конденсаторы здесь ни при чем Лампочка может моргать из-за того, что вы не установили номинальные обороты двигателя, по-этому частота тока меньше 50 ГЦ, то есть для глаза это будет заметно как моргание. Думаю нужно добавить оборотов
Цитировать
володя ж 11.12.2014 19:02 купил бензогенератор, а лампочка моргает! и стабилизатор не помогает. Может конденсаторы помогут проблеме? Спасибо
Цитировать
Лариса 02.04.2014 16:48 спасибо!!!класс но разъяснили!!!
Цитировать
Сергей 19.02.2014 07:20 3я формула со 2й как-то не клеется. По 2й получается гораздо больше. Или я что-то путаю?
Цитировать
Просто Дмитрий 11.02.2014 17:47 спасибо за инфу мне как раз это и было нужно а то в моем городе нету радио магазинов,а мне надо было из 470 микрофарад получить 400 и по идее по формуле по формуле это возможно! автор респект тебе
Цитировать
Кратер-2 12.12.2013 11:12 просто доходчиво лучше чем в инситутсиких учебниках
Цитировать
Виталик 09.12.2013 18:16 а по моему все формулы одинаковы кроме самих символов, что C1, что R1 и так далее.
Цитировать
xXx 05.12.2013 07:05 если подумать, то не так уж то и сложно
Цитировать
Власть 04.12.2013 05:59 какой то слабый у вас технарь
Цитировать
Данилп 04.12.2013 05:35 Статья классная прочитал понял и в технаре получил 10
Цитировать
Обновить список комментариев