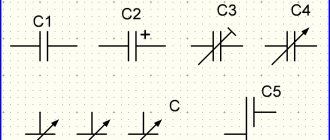Конденсаторы нашли в наше время очень широкое применение в электронике и электротехнике, ведь они являются основными элементами большинства электрических цепей и схем. Постараемся подробно в данной статье рассказать — что такое электроемкость конденсатора. Так же будут приведены применяемые формулы расчета, описаны различные виды таких устройств и рассказано об их маркировке. Кроме того будет затронуто влияние различных факторов на емкость конденсатора.
Конденсатор
Прежде чем разобраться с тем, что такое емкость простейшего конденсатора, необходимо определиться, что из себя представляет этот электроэлемент. Конденсатором является радиоэлектронная деталь, которая может накапливать и отдавать определенную порцию электрического заряда. Состоит устройство из следующих элементов:
- Корпуса. Зачастую выполняется из алюминия. По форме он может быть плоским, сферическим и цилиндрическим.
- Обкладок (2 и более). Их делают из металлических пластинок или фольги.
- Диэлектрической прокладки. Устанавливается между обкладками и служит в качестве изолятора.
- Двух или более выводных контактов для подключения устройства в электроцепь.
Работает такой накопитель электрического заряда следующим образом.
- В момент подключения элемента к источнику электрического тока, он выступает в роли проводника. В этот момент электроток имеет максимальное значение, а напряжение — минимальное.
- На обкладках элемента начинают скапливаться положительные и отрицательные заряды (электроны и ионы). Таким образом происходит зарядка самого устройства. На момент заряда сила электротока постепенно уменьшается, а напряжение наоборот — увеличивается.
- После того как количество заряда в конденсаторе станет больше допустимого предела, он разряжается и процесс опять начинает повторяться циклически.
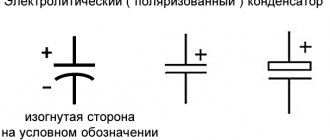
Основой работоспособности данного устройства является его емкость. Именно от этого параметра зависит время накопления заряда и общая «вместимость» устройства. О том, как на схемах обозначается простейший конденсатор, поможет понять следующий рисунок ниже.
Электрическая емкость, как и сами конденсаторы, нашли широкую область применения. Их используют в качестве:
- Частотных фильтров.
- Источника импульсов для различной фотоаппаратуры.
- Сглаживателей пульсирующих токов в выпрямителях.
- Фазосдвигающих элементов для электрических двигателей.
Применение конденсаторов в различных сферах основано именно на способности устройства накапливать электрический заряд. В более сложной электроаппаратуре эти устройства используются для бесперебойного поддержания определенного напряжения в разных накопителях данных.
Емкость
Емкостью конденсатора является физическая величина, которая определяет отношение между накопленным зарядом на обкладках и разностью потенциалов между ними.
В системе «СИ» емкость конденсатора и ее единица измерения — Фарад. В формулах для ее обозначения используется буква Ф (F). Однако емкость конденсатора редко измеряется в Фарадах, потому что это довольно большая величина. Чаще всего применяют ее кратные и дольные значения.
Значение электроемкости конденсатора всегда можно найти в маркировке устройства, которая нанесена на его корпус.
На схеме элемент обозначается буквой «С». Обозначение емкости является обязательным условием, ведь это позволит упростить процесс подбора необходимой электродетали для схемы.
От чего зависит емкость и заряд конденсатора
Емкость конденсатора это физическая величина по которой производится оценка его возможностей выполнять свои функциональные задачи.
Практическое значение емкости выражается в способности электрического устройства к накоплению заряда.
Величина напряжения на пластинах в прямой пропорции влияет на количественные характеристики заряда на обкладках. Формула определения емкости выглядит как
C = q/U,
где С — емкость конденсатора,
q — означает количество заряда на одной из пластин,
U — разница потенциалов на обкладках. Приведенная формула расчета имеет в большей степени теоретический характер.
Существует иное определение емкости, которое полезнее в практическом смысле.
В формуле C = єS/d обозначена ее связь с площадью S обкладок, расстоянием между пластинами d и свойствами диэлектрика є.
Из формулы следует, что чем больше площадь обкладок, тем больший заряд может на них разместиться и чем больше расстояние между пластинами, тем слабее заряженные частицы будут притягиваться друг к другу, увеличивая их шансы покинуть обкладку.
Максимальная диэлектрическая проницаемость материала, расположенного между пластинами, увеличивает емкость конденсатора без изменения габаритных характеристик.
Зависимость
Благодаря приведенному ранее описанию, мы узнали — что такое емкость. Далее попытаемся разобраться, от чего зависит эта характеристика. Емкость конденсатора зависит от расстояния между обкладками, их площади, а так же от самого материала диэлектрика. Благодаря этому можно сказать, от чего зависит емкость устройства: она прямопропорциональна площади пластины конденсатора и обратно пропорциональна расстоянию между пластинами.
Рассмотрим, как найти данную величину. Для плоского конденсатора формула расчета емкости выглядит следующим образом:
Зависимость способности устройства накапливать заряд от площади его обкладок и толщины диэлектрической прослойки так же указывает на то, что на данную величину оказывают влияние и общие размеры элемента.
Расчет ёмкости конденсаторов
На практике в качестве элементов, обладающих нормированной электрической ёмкостью, чаще всего используются конденсаторы, состоящие из двух плоских проводников (обкладок), разделенных диэлектриком. Формула для расчета электрической ёмкости подобного конденсатора выглядит так:
C=(S/d)*ε*ε0
где:
- С – ёмкость, Ф;
- S – площадь обкладок, кв.м;
- d – расстояние между обкладками, м;
- ε0 – электрическая постоянная, константа, 8,854*10−12 Ф/м;
- ε –электрическая проницаемость диэлектрика, безразмерная величина.
Отсюда легко понять, что ёмкость прямо пропорциональна площади обкладок и обратно пропорциональна расстоянию между проводниками. Также на ёмкость влияет материал, которым разделяются обкладки.
Расчет
Расчет емкости конденсатора делается по довольно простой формуле:
В этой формуле:
- q — величина заряда, накопленного конденсатором.
- φ1−φ2 — разница потенциалов между его обкладками.
Данное выражение помогает довольно легко рассчитать емкость любого плоского конденсатора. Как и говорилось ранее в статье, этот величина электроёмкости конденсаторов всегда зависит от его геометрических размеров.
Плоский конденсатор
Отличительная особенность плоского конденсатора — наличие двух параллельно расположенных обкладок. Такие устройства могут иметь квадратную, круглую или прямоугольную форму.
Рассмотрим далее, как определить емкость данного вида конденсаторов. Найти емкость такого типа конденсаторов всегда поможет следующая формула:
Электроемкость
Зачастую применение конденсаторов подразумевает подключение в цепь сразу нескольких таких элементов. Благодаря этому можно увеличить общую емкость. Формула для определения электроемкости плоского конденсатора при параллельном подключении выглядит следующим образом:
Определение общей емкости для такой электроцепи делается следующим образом: C=C1+C2
Величина заряда и напряжение для такой схемы соединения определяется следующим образом:
qобщ=q1+q2
Uобщ=U1=U2
Определить емкость конденсатора для последовательного соединения элементов позволит формула:
То есть в этом случае общую электроемкость плоского конденсатора находят с помощью выражения:
1/Cобщ=1/C1+1/C1
Благодаря данным выражениям найдем общее напряжение и определим величину заряда для последовательного соединения элементов:
qобщ=q1=q2
Uобщ=U1+U2
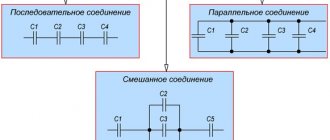
Емкость конденсатора и применяемые формулы расчетов для различных вариантов соединения плоских устройств приведены на рисунке ниже. Можно сказать, что она очень наглядная и удобная для использования:
Сферический конденсатор
Сферическое устройство имеет две обкладки в форме концентрических сфер, между которыми расположен диэлектрик. Емкость сферического конденсатора можно определить следующим образом:
В данном выражении значение «4π» определяет коэффициент рассеивания зарядов на поверхности сферических плоскостей.
Расчет емкости сферического конденсатора можно сделать по формуле для плоского устройства в том случае, если зазор по сравнению с радиусом сферы имеет довольно маленькое значение.
Цилиндрический
Цилиндрическое устройство немного схоже с ранее описанным сферическим. В них применяются схожие по форме обкладки. Они имеют так же круглую форму, а значит на расчет емкости цилиндрического устройства так же будет влиять такой параметр, как радиус обкладок. Отличием заключается только в самой вытянутой форме пластин цилиндрического конденсатора. Емкость цилиндрического конденсатора определяется по формуле:
Сферические и цилиндрические типы элементов сильно зависимы от толщины слоя диэлектрика. Чем он толще, тем меньше будет объем заряда, а значит у него повысится устойчивость к воздействию пробивного напряжения.
Схемы соединения конденсаторов — расчет емкости
В закладки
В данной статье приведены различные схемы соединения конденсаторов, а так же формулы их расчета с примером.
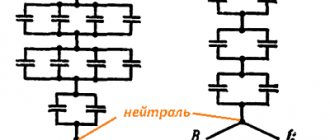
Последовательное соединение конденсаторов
Если условно разделить выводы каждого из конденсаторов на первый и второй выводы последовательное соединение конденсаторов будет выполняется следующим образом: второй вывод первого конденсатора соединяется с первым выводом второго конденсатора, второй вывод второго конденсатора, соединяется с первым выводом третьего и так далее. Таким образом мы получим группу (блок) последовательно соединенных конденсаторов с двумя свободными выводами — первым выводом первого конденсатора в блоке и вторым выводом последнего конденсатора, через которые данный конденсаторный блок и подключается в электрическую цепь.
Схема последовательного соединения конденсаторов будет иметь следующий вид:
Фактически последовательное соединение конденсаторов имеет следующий вид:
При данной схеме соединения заряды на конденсаторах будут одинаковы:
Qобщ=Q1=Q2=Q3,
где: Q1, Q2, Q3 — соответственно заряд на первом, втором, третьем и т.д. конденсаторах
Напряжение на каждом конденсаторе при такой схеме зависит от его емкости:
U1=Q/C1; U2=Q/C2; U3=Q/C3, где:
- U1, U2, U3 — соответственно напряжение на первом, втором, третьем конденсаторах
- C1, C2, C3 — соответственно емкости первого, второго, третьего конденсаторов
При этом общее напряжение составит:
Uобщ=U1+U2+U3+…+Un
Рассчитать общую емкость конденсаторов при последовательном соединении можно по следующим формулам:
- При последовательном соединении двух конденсаторов:
Собщ=(C1*C2)/(C1+C2)
- При последовательном соединении трех и более конденсаторов:
1/Собщ=1/C1+1/C2+1/C3+…+1/Cn
Параллельное соединение конденсаторов
Если условно разделить выводы каждого из конденсаторов на первый и второй выводы параллельное соединение конденсаторов будет выполняется следующим образом: первые выводы всех конденсаторов соединяются в одну общую точку (условно — точка №1) вторые выводы всех конденсаторов соединяются в другую общую точку (условно — точка №2). В результате получается группа (блок) параллельно соединенных конденсаторов подключение которой к электрической цепи производится через условные точки №1 и №2.
Схема параллельного соединения конденсаторов будет иметь следующий вид:
Таким образом параллельное соединение конденсаторов будет иметь следующий вид:
При данной схеме напряжение на всех конденсаторах будет одинаково:
U=U1=U2=U3
Заряд же на каждом из конденсаторов будет зависеть от его емкости:
Q1=U*C1; Q2=U*C2; Q3=U*C3
При этом общий заряд цепи будет равен сумме зарядов всех параллельно подключенных конденсаторов:
Qобщ=Q1+Q2+Q3…+…Qn.
Рассчитать общую емкость конденсаторов при параллельном соединении можно по следующей формуле:
Собщ=C1+C2+C3+…+Cn
Смешанное соединение конденсаторов
Схема в которой присутствует две и более группы (блока) конденсаторов с различными схемами соединения называется схемой смешанного соединения конденсаторов.
Приведем пример такой схемы:
Для расчетов такие схемы условно разделяются на группы одинаково соединенных конденсаторов, после чего расчеты ведутся для каждой группы по формулам приведенным выше.
Для наглядности приведем пример расчета общей емкости данной схемы.
Пример расчета
Условно разделив схему на группы получим следующее:
Как видно из схемы на первом этапе мы выделили 3 группы (блока) конденсаторов, при этом конденсаторы в первой и второй группе соединены последовательно, а конденсаторы в третьей группе — параллельно.
Произведем расчет каждой группы:
- Группа 1 — последовательное соединение трех конденсаторов:
1/C1,2,3 = 1/C1+1/C2+1/C3 = 1/5+1/15+1/10=0,2+0,067+0,1 = 0,367 → C1,2,3 = 1/0,367 = 2,72 мкФ
- Группа 2 — последовательное соединение двух конденсаторов:
С4,5 = (C4*C5)/(C4+C5)= (20*30)/(20+30) = 600/50 = 12 мкФ
- Группа 3 — параллельное соединение трех конденсаторов:
С6,7,8 = C6+C7+C8 = 5+25+30 = 60 мкФ
В результате расчета схема упрощается:
Как видно в упрощенной схеме осталась еще одна группа из двух параллельно соединенных конденсаторов, произведем расчет ее емкости:
- Группа 4 — параллельное соединение двух групп конденсаторов:
С1,2,3,4,5 = C1,2,3+C4,5 = 2,72+12 = 14,72 мкФ
В конечном итоге получаем простую схему из двух последовательно соединенных групп конденсаторов:
Теперь можно определить общую емкость схемы:
Собщ = (C1,2,3,4,5*C6,7,8)/(C1,2,3,4,5+C6,7,8) = 14,72*60/14,72+60 = 883,2/74,72 = 11,8 мкФ
Была ли Вам полезна данная статья? Или может быть у Вас остались вопросы? Пишите в комментариях!
Не нашли на сайте статьи на интересующую Вас тему касающуюся электрики? Напишите нам здесь. Мы обязательно Вам ответим.
↑ Наверх
5
https://elektroshkola.ru/elektrotexnicheskie-raschety/sxemy-soedineniya-kondensatorov-raschet-emkosti/
Проверка
Как отмечалось ранее, емкость устройства проставляется на его корпусе. Проверить паспортную величину и имеющуюся емкость устройства можно при помощи тестера с режимом «СХ». Например, для этого подойдут популярные модели M890D, AM-1083, DT9205A, UT139C, другие. Далее надо будет:
- Выпаять и разрядить устройство. Разрядка проводится строго изолированным металлическим предметом.
- Вставить ножки конденсатора в пазы «СХ», соблюдая полярность.
- Прибор отобразит на табло результат измерений. Его нужно будет сравнить с тем, который прописан в маркировке на его корпусе. Если значения между собой сильно отличаются, то это говорит о том, что элемент неисправный и требует замены.
Если мультиметр показал наличие бесконечной емкости, то это говорит о коротком замыкании внутри корпуса устройства и оно так же признается неисправным, требующим замены. Кроме того неисправность всегда можно определить визуально по трещинам или вздутию корпуса.