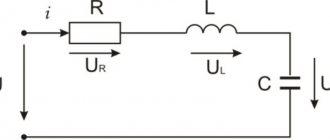
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: свободные электромагнитные колебания, колебательный контур, вынужденные электромагнитные колебания, резонанс, гармонические электромагнитные колебания.
Электромагнитные колебания
— это периодические изменения заряда, силы тока и напряжения, происходящие в электрической цепи. Простейшей системой для наблюдения электромагнитных колебаний служит колебательный контур.
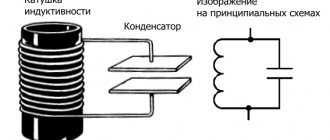
Колебательный контур
Колебательный контур
— это замкнутый контур, образованный последовательно соединёнными конденсатором и катушкой.
Зарядим конденсатор, подключим к нему катушку и замкнём цепь. Начнут происходить свободные электромагнитные колебания
— периодические изменения заряда на конденсаторе и тока в катушке. Свободными, напомним, эти колебания называются потому, что они совершаются без какого-либо внешнего воздействия — только за счёт энергии, запасённой в контуре.
Период колебаний в контуре обозначим, как всегда, через . Сопротивление катушки будем считать равным нулю.
Рассмотрим подробно все важные стадии процесса колебаний. Для большей наглядности будем проводить аналогию с колебаниями горизонтального пружинного маятника.
Начальный момент
: . Заряд конденсатора равен , ток через катушку отсутствует (рис. 1). Конденсатор сейчас начнёт разряжаться.
Рис. 1.
Несмотря на то, что сопротивление катушки равно нулю, ток не возрастёт мгновенно. Как только ток начнёт увеличиваться, в катушке возникнет ЭДС самоиндукции, препятствующая возрастанию тока.
Аналогия
. Маятник оттянут вправо на величину и в начальный момент отпущен. Начальная скорость маятника равна нулю.
Первая четверть периода
: . Конденсатор разряжается, его заряд в данный момент равен . Ток через катушку нарастает (рис. 2).
Рис. 2.
Увеличение тока происходит постепенно: вихревое электрическое поле катушки препятствует нарастанию тока и направлено против тока.
Аналогия
. Маятник движется влево к положению равновесия; скорость маятника постепенно увеличивается. Деформация пружины (она же — координата маятника) уменьшается.
Конец первой четверти
: . Конденсатор полностью разрядился. Сила тока достигла максимального значения (рис. 3). Сейчас начнётся перезарядка конденсатора.
Рис. 3.
Напряжение на катушке равно нулю, но ток не исчезнет мгновенно. Как только ток начнёт уменьшаться, в катушке возникнет ЭДС самоиндукции, препятствующая убыванию тока.
Аналогия
. Маятник проходит положение равновесия. Его скорость достигает максимального значения . Деформация пружины равна нулю.
Вторая четверть
: . Конденсатор перезаряжается — на его обкладках появляется заряд противоположного знака по сравнению с тем, что был вначале (рис. 4).
Рис. 4.
Сила тока убывает постепенно: вихревое электрическое поле катушки, поддерживая убывающий ток, сонаправлено с током.
Аналогия
. Маятник продолжает двигаться влево — от положения равновесия к правой крайней точке. Скорость его постепенно убывает, деформация пружины увеличивается.
Конец второй четверти
. Конденсатор полностью перезарядился, его заряд опять равен (но полярность другая). Сила тока равна нулю (рис. 5). Сейчас начнётся обратная перезарядка конденсатора.
Рис. 5.
Аналогия
. Маятник достиг крайней правой точки. Скорость маятника равна нулю. Деформация пружины максимальна и равна .
Третья четверть
: . Началась вторая половина периода колебаний; процессы пошли в обратном направлении. Конденсатор разряжается (рис. 6).
Рис. 6.
Аналогия
. Маятник двигается обратно: от правой крайней точки к положению равновесия.
Конец третьей четверти
: . Конденсатор полностью разрядился. Ток максимален и снова равен , но на сей раз имеет другое направление (рис. 7).
Рис. 7.
Аналогия
. Маятник снова проходит положение равновесия с максимальной скоростью , но на сей раз в обратном направлении.
Четвёртая четверть
: . Ток убывает, конденсатор заряжается (рис. 8).
Рис. 8.
Аналогия
. Маятник продолжает двигаться вправо — от положения равновесия к крайней левой точке.
Конец четвёртой четверти и всего периода
: . Обратная перезарядка конденсатора завершена, ток равен нулю (рис. 9).
Рис. 9.
Данный момент идентичен моменту , а данный рисунок — рисунку 1. Совершилось одно полное колебание. Сейчас начнётся следующее колебание, в течение которого процессы будут происходить точно так же, как описано выше.
Аналогия
. Маятник вернулся в исходное положение.
Рассмотренные электромагнитные колебания являются незатухающими
— они будут продолжаться бесконечно долго. Ведь мы предположили, что сопротивление катушки равно нулю!
Точно так же будут незатухающими колебания пружинного маятника при отсутствии трения.
В реальности катушка обладает некоторым сопротивлением. Поэтому колебания в реальном колебательном контуре будут затухающими. Так, спустя одно полное колебание заряд на конденсаторе окажется меньше исходного значения. Со временем колебания и вовсе исчезнут: вся энергия, запасённая изначально в контуре, выделится в виде тепла на сопротивлении катушки и соединительных проводов.
Точно так же будут затухающими колебания реального пружинного маятника: вся энергия маятника постепенно превратится в тепло из-за неизбежного наличия трения.
Осциллограф
Но если колебания физических тел наблюдать легко, то колебания электромагнитного поля обнаружить без специальных приборов нельзя. Ведь увидеть изменения заряда, силы тока или напряжения невозможно. Использовать для этого электроизмерительные приборы (гальванометры, вольтметры или амперметры) тоже неудобно, поскольку электромагнитные колебания происходят с гораздо большей частотой по сравнению с механическими. Поэтому специально для визуализации электромагнитных колебаний был создан прибор, который называется осциллографом.
Осциллограф, схему которого вы видите ниже, представляет собой электронно-лучевую трубку. Через нее проходит узкий пучок электронов и попадает на экран, который начинает светиться при бомбардировке электронами.
На горизонтально отклоненные пластины трубки подается переменное напряжение развертки up пилообразной формы (см. рисунок ниже). Оно медленно нарастает и быстро падает. Поэтому электрическое поле между пластинами заставляет электронный луч пробегать экран в горизонтальном направлении с постоянной скоростью и затем почти мгновенно возвращаться назад. После этого весь процесс повторяется.
Если же присоединить вертикально отклоняющие пластины трубки к конденсатору, то колебания напряжения при его разрядке вызовут колебания луча в вертикальном направлении. В результате на экране осциллографа образуется временная развертка колебаний. Она напоминает синусоиду или косинусоиду подобно той, с помощью которой можно описать механические колебания.
С течением времени электромагнитные колебания затухают. Такие колебания являются свободными. Напомним, что свободными колебаниями называют такие колебания, которые возникают в колебательной системе после выведения ее из положения равновесия. В нашем случае система выводится из равновесия при сообщении конденсатору заряда. Зарядка конденсатора эквивалента отклонения математического маятника от положения равновесия.
В электрической цепи также можно получить вынужденные колебания, которые будут происходить до тех пор, пока на колебательную систему действует периодическая внешняя сила. Вынужденными электромагнитными колебаниями называют колебания в цепи под действием внешней периодической электродвижущей силы.
Энергетические превращения в колебательном контуре
Продолжаем рассматривать незатухающие колебания в контуре, считая сопротивление катушки нулевым. Конденсатор имеет ёмкость , индуктивность катушки равна .
Поскольку тепловых потерь нет, энергия из контура не уходит: она постоянно перераспределяется между конденсатором и катушкой.
Возьмём момент времени, когда заряд конденсатора максимален и равен , а ток отсутствует. Энергия магнитного поля катушки в этот момент равна нулю. Вся энергия контура сосредоточена в конденсаторе:
Теперь, наоборот, рассмотрим момент, когда ток максимален и равен , а конденсатор разряжен. Энергия конденсатора равна нулю. Вся энергия контура запасена в катушке:
В произвольный момент времени, когда заряд конденсатора равен и через катушку течёт ток , энергия контура равна:
Таким образом,
(1)
Соотношение (1) применяется при решении многих задач.
Электромеханические аналогии
В предыдущем листке про самоиндукцию мы отметили аналогию между индуктивностью и массой. Теперь мы можем установить ещё несколько соответствий между электродинамическими и механическими величинами.
Для пружинного маятника мы имеем соотношение, аналогичное (1):
(2)
Здесь, как вы уже поняли, — жёсткость пружины, — масса маятника, и — текущие значения координаты и скорости маятника, и — их наибольшие значения.
Сопоставляя друг с другом равенства (1) и (2), мы видим следующие соответствия:
(3)
(4)
(5)
(6)
Опираясь на эти электромеханические аналогии, мы можем предвидеть формулу для периода электромагнитных колебаний в колебательном контуре.
В самом деле, период колебаний пружинного маятника, как мы знаем, равен:
B соответствии с аналогиями (5) и (6) заменяем здесь массу на индуктивность , а жёсткость на обратную ёмкость . Получим:
(7)
Электромеханические аналогии не подводят: формула (7) даёт верное выражение для периода колебаний в колебательном контуре. Она называется формулой Томсона
. Мы вскоре приведём её более строгий вывод.
Гармонический закон колебаний в контуре
Напомним, что колебания называются гармоническими
, если колеблющаяся величина меняется со временем по закону синуса или косинуса. Если вы успели забыть эти вещи, обязательно повторите листок «Механические колебания».
Колебания заряда на конденсаторе и силы тока в контуре оказываются гармоническими. Мы сейчас это докажем. Но прежде нам надо установить правила выбора знака для заряда конденсатора и для силы тока — ведь при колебаниях эти величины будут принимать как положительные, так и отрицательные значения.
Сначала мы выбираем положительное направление обхода
контура. Выбор роли не играет; пусть это будет направление
против часовой стрелки
(рис. 10).
Рис. 10. Положительное направление обхода
Сила тока считается положительной , если ток течёт в положительном направлении. В противном случае сила тока будет отрицательной .
Заряд конденсатора — это заряд той его пластины, на которую
течёт положительный ток (т. е. той пластины, на которую указывает стрелка направления обхода). В данном случае — заряд
левой
пластины конденсатора.
При таком выборе знаков тока и заряда справедливо соотношение: (при ином выборе знаков могло случиться ). Действительно, знаки обеих частей совпадают: если , то заряд левой пластины возрастает, и потому .
Величины и меняются со временем, но энергия контура остаётся неизменной:
(8)
Стало быть, производная энергии по времени обращается в нуль: . Берём производную по времени от обеих частей соотношения (8); не забываем, что слева дифференцируются сложные функции (Если — функция от , то по правилу дифференцирования сложной функции производная от квадрата нашей функции будет равна: ):
Подставляя сюда и , получим:
Но сила тока не является функцией, тождественно равной нулю; поэтому
Перепишем это в виде:
(9)
Мы получили дифференциальное уравнение гармонических колебаний вида , где . Это доказывает, что заряд конденсатора колеблется по гармоническому закону (т.е. по закону синуса или косинуса). Циклическая частота этих колебаний равна:
(10)
Эта величина называется ещё собственной частотой
контура; именно с этой частотой в контуре совершаются свободные (или, как ещё говорят,
собственные
колебания). Период колебаний равен:
Мы снова пришли к формуле Томсона.
Гармоническая зависимость заряда от времени в общем случае имеет вид:
(11)
Циклическая частота находится по формуле (10); амплитуда и начальная фаза определяются из начальных условий.
Мы рассмотрим ситуацию, подробно изученную в начале этого листка. Пусть при заряд конденсатора максимален и равен (как на рис. 1); ток в контуре отсутствует. Тогда начальная фаза , так что заряд меняется по закону косинуса с амплитудой :
(12)
Найдём закон изменения силы тока. Для этого дифференцируем по времени соотношение (12), опять-таки не забывая о правиле нахождения производной сложной функции:
Мы видим, что и сила тока меняется по гармоническому закону, на сей раз — по закону синуса:
(13)
Амплитуда силы тока равна:
Наличие «минуса» в законе изменения тока (13) понять не сложно. Возьмём, к примеру, интервал времени (рис. 2).
Ток течёт в отрицательном направлении: . Поскольку , фаза колебаний находится в первой четверти: . Синус в первой четверти положителен; стало быть, синус в (13) будет положительным на рассматриваемом интервале времени. Поэтому для обеспечения отрицательности тока действительно необходим знак «минус» в формуле (13).
А теперь посмотрите на рис. 8. Ток течёт в положительном направлении. Как же работает наш «минус» в этом случае? Разберитесь-ка, в чём тут дело!
Изобразим графики колебаний заряда и тока, т.е. графики функций (12) и (13). Для наглядности представим эти графики в одних координатных осях (рис. 11).
Рис. 11. Графики колебаний заряда и тока
Обратите внимание: нули заряда приходятся на максимумы или минимумы тока; и наоборот, нули тока соответствуют максимумам или минимумам заряда.
Используя формулу приведения
запишем закон изменения тока (13) в виде:
Сопоставляя это выражение с законом изменения заряда , мы видим, что фаза тока, равная , больше фазы заряда на величину . В таком случае говорят, что ток опережает по фазе
заряд на ; или
сдвиг фаз
между током и зарядом равен ; или
разность фаз
между током и зарядом равна .
Опережение током заряда по фазе на графически проявляется в том, что график тока сдвинут влево
на относительно графика заряда. Сила тока достигает, например, своего максимума на четверть периода раньше, чем достигает максимума заряд (а четверть периода как раз и соответствует разности фаз ).
Частота собственного резонанса катушки
На заре развития радиотехники было обнаружено, что катушка не идеальная индуктивность. На определенной частоте она входит в режим резонанса даже при отсутствии внешней емкости, а выше этой частоты импеданс катушки носит уже емкостный характер. Для объяснения этого явления предположили, что кроме индуктивности реальная катушка обладает еще собственной емкостью (предположительно между соседними витками) и реальную катушку стали представлять в виде модели из сосредоточенных RLC элементов, в которой L — индуктивность, C — собственная емкость, названная паразитной, а с помощью активного R учитываются различные потери в катушке. Такая модель катушки имеет одну резонансную частоту, которую назвали частотой собственного резонанса. Долгое время эта модель всех устраивала и стала классической моделью реальной катушки во всех учебниках.
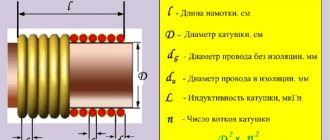
Ведь катушки в подавляющем большинстве практических применений работают на частотах намного ниже частоты собственного резонанса и задачей конструктора является, по сути, обеспечение этого условия. При этом большинство инженеров с этой целью пытались уменьшить эту самую «межвитковую» паразитную емкость. В случае же, если катушка работает на частотах близких к собственному резонансу, как например в спиральных резонаторах или катушках Теслы, RLC-модель дает неверные результаты, но для таких случаев были разработаны альтернативные алгоритмы расчета и все остались довольны не особо задумываясь о причинах таких нестыковок. В нашу цифровую эпоху появились программы, которые дали возможность моделировать поведение любых высокочастотных устройств с высокой степени точности — так называемые электромагнитные симуляторы. Это мощные пакеты типа CST Studio, HFSS и многие другие. Давайте проведем исследование однослойной спиральной катушки в программе HFSS. В первой модели мы поместим катушку над идеальной проводящей поверхностью и запитаем от точечного источника с внутренним сопротивлением 50 МОм. Второй конец катушки заземлен. Расчет будем вести в режиме HFSS Design, использующий метод конечных элементов.
Вторую катушку рассчитаем методом HFSS Design-IE, использующий метод моментов. В отличии от популярных у радиолюбителей симуляторов на основе ядра NEC, например MMANA, здесь сегментация идет не на отрезки провода, а по его поверхности на элементарные треугольные площадки. При такой сегментации для успешного расчета требуется не менее 8-16 Гб оперативной памяти компьютера. Запитаем катушку через короткие выводы от такого же источника. Поскольку катушка не заземлена, в этой модели первый резонанс — полуволновой.
В результате исследования мы получили графики импеданса на зажимах источника относительно частоты. Из графиков видно, что у катушки не один, а множество резонансов. Из этого следует вывод, что наша катушка — это совсем не одиночный LC-контур с собственной индуктивностью и паразитной емкостью в виде сосредоточенных элементов, как принято считать, а длинная линия с распределенными параметрами. Такая линия состоит из одного провода, но это не должно никого смущать. То, что в даже одиночном проводе наблюдаются волновые резонансные явления, хорошо иллюстрирует пример полуволнового вибратора Герца. Ведь волновые явления как в длинных линиях, так и в вибраторе отображают тот факт, что электромагнитное взаимодействие распространяется с конечной скоростью. На то чтобы электромагнитное взаимодействие «добралось» от одного конца провода до другого затрачивается определенное время, и когда это время сравнимо с периодом колебаний рабочей частоты возникают явления резонанса. И катушка в этом плане недалеко ушла от вибратора, поскольку несмотря на малые ее габариты, длина провода, которым она намотана, может иметь величину сравнимую с длиной волны. Частоту собственного резонанса вибратора мы можем довольно легко определить зная его длину, учтя коэффициент укорочения. В катушке, кроме того, необходимо учесть связь между витками.
В учебниках по электродинамике [1] можно найти описание работы спиральных волноводов с поверхностными электромагнитными (ЭМ) волнами, распространяющимися вдоль провода спирали. Такие волноводы применяются как замедляющие структуры в спиральных антеннах и лампах бегущей волны. Длина одного витка и шаг намотки у них сравним с длиной волны. В частности, у спиральной антенны длина витка L равна длине волны, а шаг намотки p равен четверти длины волны.Фазовая скорость волны вдоль оси спирального волновода значительно ниже скорости света, на чем и основано его применение как замедляющей структуры.
| [1] |
где:
- vax — скорость волны вдоль оси спирали
- с — скорость света
Относительная фазовая скорость волны вдоль оси такого волновода зависит только от геометрии спирали и не зависит от частоты, поскольку влияние витков друг на друга минимально и ЭМ-волна распространяется вдоль провода такой спирали, так же как и у вибратора. Отметим, что фазовая скорость ЭМ волны относительно провода спирали в таком волноводе близка к скорости света.
В нашей же катушке, и длина отдельного витка, и даже длина всей намотки, и тем более шаг намотки намного меньше длины волны. В этом случае, кроме основной моды в таком спиральном волноводе существуют высшие моды колебаний, распространяющиеся непосредственно вдоль ее оси. Другими словами, ЭМ волна распространяется не только вдоль длины провода, но часть ее «перепрыгивает от витка к витку». Относительная фазовая скорость вдоль оси катушки определяется следующим приближенным выражением:
| [2] |
где:
- λ0 — длина волны рабочей частоты в свободном пространстве
Как видно из формулы, скорость зависит от диаметра катушки, шага намотки и длины волны. По сути, катушка — тот же спиральный волновод с медленными волнами, но работающий в другом режиме колебаний. Во избежании различных спекуляций отметим то обстоятельство, что благодаря наличию высших мод, волна «добирается» до другого конца катушки быстрее чем непосредственно вдоль провода. Поэтому фазовая скорость волны относительно провода выше скорости света, причем в разы. Это не противоречит теории относительности. Достаточно упомянуть, что в полых волноводах фазовая скорость волны тоже выше скорости света. Для понимания этого кажущегося парадокса следует различать фазовую и групповую скорости электромагнитной волны. Для чего отсылаю к учебникам…
Катушка с одним заземленным концом резонирует на частотах nλ0/4, где n – целое число, λ0 — длина волны рабочей частоты и fsrf = vax/λ0. Поэтому увеличение частоты собственного резонанса сводится к увеличению значения vax. Из-за наличия высших мод ЭМ-волны, частота первого резонанса катушки всегда выше частоты, рассчитанной исходя из длины провода. По этой же причине высшие по частоте резонансы не кратны первому и друг другу. При изменении шага намотки vax имеет максимум при шаге спирали примерно равном радиусу намотки (радиус a = D / 2). Однако катушки с большим шагом намотки (p ≈ a) не представляют практического интереса, поскольку имеют малую индуктивность. При увеличении шага намотки частота собственного резонанса катушки растет (при p < a), но рост этот идет за счет снижения величины индуктивности. При фиксированной индуктивности, если увеличивать шаг намотки, нам приходится добавлять витки и выигрыша мы практически не получаем.
У коротких катушек на каркасах большого диаметра последующие резонансы отстоят от первого далеко выше по частоте, что можно видеть по результатам HFSS моделирования:
На частотах много ниже частоты первого резонанса пространственные задержки намного меньше периода колебаний, ЭМ-поле вокруг катушки представляет собой поле соленоида и скорость распространения волны вдоль ее оси можно не учитывать. В таком случае RLC-модель из сосредоточенных элементов будет вполне рабочей и достаточно точно отображает поведение катушки. Стоит только помнить, что паразитная собственная емкость — это вовсе не статическая емкость между витками. В таком режиме работают катушки из всех наших трех моделей в КВ диапазоне и ниже. Однако уже на частоте первого резонанса начинают проявляться волновые эффекты, связанные с ограниченной скоростью передачи электромагнитных взаимодействий и катушку следует рассматривать только как спиральный волновод. В этом случае RLC модель не только не годится для расчетов, но и приводит к неверному пониманию самого механизма возникновения резонансных явлений в катушке. В этой связи хочется отметить наличие в Сети ложной идеи о том, что в катушке одновременно происходят как волновой резонанс, так и LC-резонанс на сосредоточенных индуктивности и пресловутой «межвитковой емкости». Такое утверждение равносильно тому, что в катушке имеются два механизма распространения электромагнитных взаимодействий. Один происходит, как обычно, со скоростью света и определяет волновой резонанс. Второй осуществляется мгновенно с бесконечной скоростью в виртуальных сосредоточенных элементах катушки. Ведь фазовый сдвиг между током и напряжением в реактивных элементах — это совсем не то пространственное запаздывание, о котором идет речь. На самом деле катушка, как набор сосредоточенных RLC элементов, и катушка, как цепь с распределенными параметрами — это две разные математические модели одной и той же реальной катушки. Первая модель не учитывает ограниченную скорость передачи взаимодействий, основана на предположении, что плотность тока во всех витках всегда одинакова, что не имеет место при собственном резонансе спирали. Поэтому эта модель ограничена и применима только на низких частотах. Вторая модель — более полная, учитывает то, что не учла первая и применима на любой частоте. В этом нет ничего необычного. Любая цепь, физические размеры которой сравнимы с длиной волны, не может рассматриваться как цепь из сосредоточенных элементов, в которой не учитывается ограниченная скорость передачи электромагнитных взаимодействий. Именно по этой причине , а заодно кстати и само абстрактное математическое понятие «индуктивность». Как положительную реактивность.
Особо хотелось бы отметить следующий момент. На низких частотах, где, как мы выяснили, RLC модель справедлива, можно считать, что как индуктивность так и собственная емкость катушки не зависят от частоты, а определяются только геометрией намотки. Это общеизвестный факт, который зафиксирован например в формуле Нагаока. Однако реально параметры спиральной длинной линии зависят от частоты. Не только vax, но и погонная емкость и погонная индуктивность и, как следствие — величины собственной индуктивности и собственной емкости катушки в целом. Только на низких частотах эта зависимость пренебрежимо мала, а вот уже на частотах близких к первому резонансу значения индуктивности и собственной емкости катушки начинают заметно «плыть» по частоте. В итоге, мы сталкиваемся с ситуацией, что эти значения, измеренные или рассчитанные на низкой частоте, не пригодны для расчета частоты собственного резонанса катушки как LC резонанса по формуле Томсона. Расчет даст неверный результат! Неверный, Карл! Таким образом, мы приходим к выводу, что расчеты, основанные на понятии о LC-резонансе в катушке, полностью теряют смысл, что еще раз доказывает несостоятельность RLC-модели катушки не только для объяснения физических явлений при собственном резонансе, но и для расчетов в этой частотной области. Поэтому приходится прибегать к более сложному численному методу из работы [5], включающему в себя функции Бесселя и прочий суровый , что и делает Coil32.
Как видно из HFSS-моделей, у катушки как первый резонанс так и все последующие связаны исключительно с волновыми явлениями в катушке. Возможны практические случаи, когда катушка работает в диапазоне частот, в который попадает не только ее первый резонанс, но и более высокие. Очень хорошо такой случай описан в статье И.Гончаренко об анодном дросселе коротковолнового передатчика [2]. На этом примере хорошо видно, что для правильного понимания механизма резонансных явлений в катушке необходимо пользоваться теорией длинных линий.
Кроме фазовой скорости волны в катушке на частоту собственного резонанса оказывает влияние так называемый торцевой эффект, подобный хорошо известному аналогичному понятию из теории антенн, от которого зависит коэффициент укорочения вибратора. Этот эффект проявляется от того, что ЭМ-поле вокруг катушки занимает пространство большее, чем сама катушка. Наличие торцевого эффекта понижает резонансную частоту и этот эффект более выражен у коротких катушек с большим диаметром, что еще раз подтверждает родственную связь резонансных явлений в катушке и в вибраторе. Учитывая фазовую скорость вдоль оси катушки и явление торцевого эффекта мы можем рассчитать частоту собственного резонанса катушки по следующей весьма приближенной формуле от G3RBJ:
| [3] |
где:
- fsrf — частота собственного резонанса [МГц]
- ĺw — длина провода катушки с учетом торцевого эффекта [м]
- lw — реальная длина провода катушки [м]
- D, p, l — диаметр, шаг и длина намотки, соответственно [м]
- 0,25 — коэффициент, определяющий четвертьволновый резонанс (для полуволнового — 0,5)
Если конструктору необходимо создать катушку, имеющую минимальные габариты и максимальную частоту собственного резонанса при заданной индуктивности, то наиболее оптимальна будет намотка с расстоянием между витками, равном диаметру провода, при отношении l/D ≈ 1..1,5. Хотелось бы обратить внимание конструкторов, что здесь идет речь о вычислении собственной резонансной частоты «голой катушки в вакууме», т.е. одной проволочной спирали без учета влияния каркаса, сердечника, экрана, изоляции провода и т.п. Все эти, трудно поддаваемые учету факторы, приводят к уменьшению этой частоты. Причем влияние оказывает все — любой проводник, печатная плата, корпус конструкции. В наших HFSS-моделях влияющие факторы — это выводы спирали и, особенно, сплошная земля в 1-ой и 3-ей моделях. Даже если вы соберетесь измерить частоту собственного резонанса экспериментально, это будет непростой задачей, так как щупы измерительного оборудования также оказывают влияние, даже если катушка где то висит в воздухе!
Необходимо отметить, что строгого аналитического решения уравнений Максвелла для цилиндрической проволочной спирали не существует, поэтому в теории спиральный волновод представляют в виде эквивалентной модели из тонкостенного сплошного цилиндра с анизотропной проводимостью. Однако численные методы решения уравнений Максвелла (чем в принципе и занимается HFSS) приводят нас к вполне однозначным результатам. В итоге, следует иметь ввиду, что вышеприведенная простая аналитическая формула [3] является весьма приблизительной и не может быть применима к любой катушке с произвольной геометрией намотки. Поэтому в Coil32 расчет частоты собственного резонанса основан не на аналитическом, а на численном методе из работы [5], который проверен практическими измерениями. При этом не учитывается влияние экрана, каркаса и других факторов. Расчет имеет точность около 10% при 0,04 < l/D < 40. Для некоторых катушек, например для очень длинных соленоидов с большим числом витков, этот метод может давать неверный результат. На практике же следует придерживаться следующего простого условия: если длина провода, которым намотана катушка, меньше четверти длины волны на наивысшей рабочей частоте, то катушка будет работать ниже своего первого резонанса.
P.S: В заключении хотелось бы добавить несколько слов о концепции «». Эта концепция зиждется на трех ложных в своей основе предпосылках и поэтому в корне неверна:
- Любую линейную замкнутую электрическую цепь можно представить как набор из сосредоточенных RLC-элементов. Основными законами этой цепи являются законы Ома и Кирхгофа. Любое изменение топологии цепи или добавление элементов в нее полностью меняет распределение токов и напряжений во всей цепи. Однако в концепции «двойного резонанса» длинная линия считается этаким себе «черным ящиком», равноценным какому-то особому четвертому сосредоточенному элементу, волновые процессы внутри которого существуют сами по себе. Но не стоит забывать, что другое название длинной линии — линия с распределенными параметрами, когда она представляется как цепь из бесконечного числа RLC-элементов. В ней также справедливы те же самые законы Ома и Кирхгофа, только представленные уже в . Мы просто перешли на более высокий уровень математической абстракции, при котором учитываются пространственно-временные задержки сигнала, но сути дела это не меняет. Поэтому, если мы подключим параллельно такой линии сосредоточенную емкость и будем считать, что характер распределения токов и напряжений внутри самой линии не изменится, мы просто отрицаем сами законы Ома и Кирхгофа. При этом не надо забывать, что характер распространения ЭМ-волны в линии и характер распределения токов и напряжений в ней — вещи жестко взаимосвязанные. Вывод — волновые процессы в линии не являются каким то особым ее свойством, которое существует само по себе, независимо от общих законов электрических цепей. Эти законы настолько фундаментальны, что в определенной мере отображены на еще более высоком уровне математической абстракции в , которые описывают свойства самой электромагнитной волны. Итог: «На волновой процесс ёмкость C1 не оказывает почти никакого влияния» — ложное утверждение.
- «При сворачивании линии в спираль мало что меняется». Это утверждение неверно. По крайней мере индуктивность значительно увеличивается, иначе зачем сворачивать? Кроме того, погонная емкость и погонная индуктивность такой линии уже становятся зависимыми от частоты. В результате, как отмечалось выше, формула Томсона для расчета частоты собственного резонанса в спиральной линии перестает работать.
- В итоге, на основе этих неверных предпосылок, утверждается наличие двух независимых резонансов и нам выкатывают две формулы. Формулу Томсона, которая на самом деле в этом случае не работает, и формулу от Alane Payne (G3RBJ), которая, как мы отметили выше, является сильно приближенной. И по этим двум формулам уже идет развитие «теории двух независимых резонансов», которых в реальности не существует, что подтверждают и расчеты в HFSS и . Повторюсь еще раз — все дело в разных математических моделях одной реальной катушки и разных уровнях математических абстракций в зависимости от конкретных условий расчета. Смешивать все это в одну кучу и подгонять под выдуманную теорию нельзя.
Ссылки по теме:
- Техническая электродинамика
, Семенов Н.А., Изд. «Связь» Москва, 1973, стр.318-323. - — И.Гончаренко 2007-2012
- — И.Гончаренко
- Высокочастотные катушки, спиральные резонаторы и увеличение напряжения из-за когерентных пространственных мод 2001г. (Оригинал статьи )
- — applicable theory, models and calculation methods. By David W Knight (G3YNH)
- — основная статья с массой полезных ссылок по теме, в том числе на экспериментальные исследования с наглядными фото (G3YNH)
- and the self-capacitance myth. By Alane Payne (G3RBJ)
- О собственной емкости катушки.