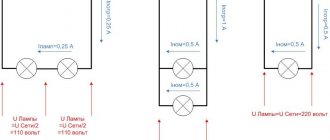
Когда к цепи (рис. 6.2.1) с параллельным соединением резистора и конденсатора подается переменное синусоидальное напряжение, одно и то же напряжение приложено к обоим компонентам цепи.
Общий ток цепи I разветвляется на ток в конденсаторе IC(емкостная составляющая общего тока) и ток в резисторе IR(активная составляющая).
Между токами I, IC и IR существуют фазовые сдвиги, обусловленные емкостным реактивным сопротивлением XC конденсатора. Они могут быть представлены с помощью векторной диаграммы токов (рис. 6.2.2).
В треугольнике проводимостей G=1/R, BC=1/XC, а Y представляет собой так называемую полную проводимость цепи в См, тогда как G – активная, а BC– реактивная (емкостная) проводимости.
Из-за фазового сдвига между током и напряжением в цепях, подобных данной, простое арифметическое сложение действующих или амплитудных токов в параллельных ветвях невозможно. Но в векторной форме:I = IR +IC.
Расчет ведется по следующим формулам, вытекающим из векторной диаграммы и треугольника проводимости:
Для цепи с параллельным соединением резистора и конденсатора измерьте действующие значения тока в резисторе IR и конденсаторе I C, полный ток I и вычислите угол сдвига фаз j, полное сопротивление цепи Z и емкостную реактивную проводимость BC.
· Соберите цепь согласно схеме (рис. 6.2.4), подсоедините регулируемый источник синусоидального напряжения и установите его параметры: U = 5 В, f = 1 кГц.
· Выполните измерения U, I, IC, IR и занесите результаты в табл. 6.2.1. Если измерения производите виртуальными приборами, то измерьте также R, j, XC, Z.
| U, B | I, мА | IС, мА | IR, мА | j, град | R, Ом | XC, Ом | Z, Ом | Примечание |
| Расчет | ||||||||
| Вирт. Изм |
Емкостные реактивные проводимость и сопротивление цепи
· Сравните результаты вычислений с результатами виртуальных измерений (если они есть).
Какое освещение Вы предпочитаете
ВстроенноеЛюстра
· Постройте векторную диаграмму токов (рис. 6.2.5) и треугольник проводимостей (рис. 6.2.6).
Последовательное соединение резистора и катушки индуктивности
Когда к цепи (рис. 6.3.1) с последовательным соединением резистора и катушки индуктивности подается переменное синусоидальное напряжение, один и тот же синусоидальный ток имеет место в обоих компонентах цепи.
| U, B | I, мА | IС, мА | IR, мА | j, град | R, Ом | XC, Ом | Z, Ом | Примечание |
| Расчет | ||||||||
| Вирт. Изм |
Параллельное соединение резистора и конденсатора
Зная плотность энергии поля в каждой точке, можно найти энергию поля, заключенного в любом объеме V
. Для этого нужно вычислить интеграл:
Мнение эксперта
It-Technology, Cпециалист по электроэнергетике и электронике
Задавайте вопросы «Специалисту по модернизации систем энергогенерации»
Напряжение при параллельном соединении — формула, сила тока, соединение конденсаторов и резисторов Для цепи с параллельным соединением резистора и конденсатора измерьте действующие значения тока в резисторе I R и конденсаторе I C , полный ток I и вычислите угол сдвига фаз j , полное сопротивление цепи Z и емкостную реактивную проводимость B C. Спрашивайте, я на связи!
ОПРЕДЕЛЕНИЯ
- характеристика проводника, количественная мера его способности удерживать электрический заряд
- количественная характеристика, показывающая степень возможного участия тела в электромагнитных взаимодействиях
- устройство, предназначенное для получения нужных величин электрической ёмкости и способное накапливать и отдавать (перераспределять) электрические заряды
- разность потенциалов между двумя точками электрической цепи; на участке цепи, не содержащей электродвижущую силу, равно произведению силы тока на сопротивление участка
Напряжение при параллельном соединении
Будет интересно➡ Сколько стоят керамические конденсаторы?
При параллельном соединении через каждый конденсатор потечет одельный ток, в зависимости от емкости конденсатора:
Мнение эксперта
It-Technology, Cпециалист по электроэнергетике и электронике
Задавайте вопросы «Специалисту по модернизации систем энергогенерации»
15. Соединение конденсаторов (параллельное и последовательное) Из-за того, что поперечное сечение реальных проводников составляет десятки мм2, за единицу удельного сопротивления выбирают Ом мм2 м. Спрашивайте, я на связи!
Формула энергии конденсатора
Напряжения на различных конденсаторах будут, вообще говоря, различными, так как для заряда одним и тем же количеством электричества конденсаторов различной емкости всегда требуются различные напряжения.
Типы соединений конденсаторов.
Чем меньше емкость конденсатора, тем большее напряжение необходимо для того, чтобы зарядить этот конденсатор требуемым количеством электричества, и наоборот.
Таким образом, при заряде группы конденсаторов, соединенных последовательно, на конденсаторах малой емкости напряжения будут больше, а на конденсаторах большой емкости — меньше.
Последовательное соединение конденсаторов – это соединение двух или более конденсаторов в форме цепи, в которой каждый отдельный конденсатор соединяется с другим отдельным конденсатором только в одной точке. Ток (iC), заряжающий последовательную цепь конденсаторов, будет одинаковым для всех конденсаторов, поскольку у него есть только один возможный путь прохождения.
Переменный ток
Господа, как-то раз чудесным летним деньком я взял ноутбук и вышел из дома на дачный участок. Там, усевшись в кресле-качалке в тени яблонь, я и решил написать данную статью. Ветерок шумел в ветвях деревьев, раскачивая их из стороны в сторону, и в воздухе была та самая атмосфера, благоприятствующая течению мыслей, которая так порой необходима…
Впрочем, хватит лирики, пора переходить непосредственно к существу обозначенного в заголовке статьи вопроса.
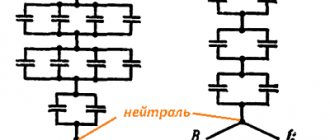
Итак, параллельное соединение конденсаторов… Что вообще такое параллельное соединение? Те, кто читал мои прошлые статьи, безусловно, помнят значение этого определения. Оно нам встречалось, когда мы говорили про параллельное соединение резисторов. В случае конденсаторов определение будет иметь абсолютно такой же вид. Итак, параллельное соединение конденсаторов – это такое соединение, когда одни концы всех конденсаторов соединены в один узел, а другие – в другой.
Конечно, лучше один раз увидеть, чем сто раз услышать, поэтому на рисунке 1 я привел изображение трех конденсаторов, которые соединены параллельно. Пусть емкость первого равна С1, второго – С2, а третьего – С3.
Рисунок 1 – Параллельное соединение конденсаторов
В данной статье мы разберем, по каким законам изменяются токи, напряжения и сопротивления переменному току при параллельном соединении конденсаторов, а также какова будет суммарная емкость такой конструкции. Ну и, само собой, поговорим, зачем вообще такое соединение может быть нужно.
Предлагаю начать с напряжения, ибо с ним здесь все предельно ясно. Господа, должно быть совершенно очевидно, что при параллельном соединении конденсаторов напряжения на них равны между собой. То есть напряжение на первом конденсаторе точно такое же, как на втором и на третьем
Почему, собственно, это так? Да очень просто! Напряжение на конденсаторе считается как разность потенциалов между двумя ножками конденсатора. А при параллельном соединении «левые» ножки всех конденсаторов сходятся в один узел, а «правые» – в другой. Таким образом, «левые» ножки всех конденсаторов имеют один потенциал, а «правые» другой. То есть разность потенциалов между «левой» и «правой» ногами будет одинаковая для любого конденсатора, а это как раз и значит, что на всех конденсаторах одно и то же напряжение. Чуть более строгий вывод этого утверждения вы можете глянуть вот в этой статье. В ней мы приводили его для параллельного соединения резисторов, но и здесь он будет звучать абсолютно так же.
Итак, мы выяснили, что напряжение на всех параллельно соединенных конденсаторах одно и то же. Это, кстати, верно для любого вида напряжения – как для постоянного, так и для переменного. Вы можете присоединить к трем параллельно включенным конденсаторам батарейку на 1,5 В. И на всех них будет постоянные 1,5 В. А можете присоединить к ним генератор синусоидального напряжения с частотой 50 Гц и амплитудой 310 В. И на каждом конденсатор будет синусоидальное напряжение с частотой 50 Гц и амплитудой 310 В. Важно помнить, что у параллельно соединенных конденсаторов одной и той же будет не только амплитуда, но и частота, и фаза напряжения.
И если с напряжением все вот так вот просто, то с током ситуация посложнее. Когда мы говорим про ток через конденсатор, то обычно имеем ввиду переменный ток. Вы ведь помните, что постоянные токи через конденсаторы не текут? Конденсатор для постоянного тока – это все равно, что разрыв цепи (на деле есть некоторое сопротивление утечки конденсатора, но им обычно пренебрегают, потому что оно очень велико). Переменные же токи вполне себе текут через конденсаторы, причем могут иметь при этом весьма и весьма большие амплитуды. Очевидно, что эти переменные токи вызываются некоторым переменными напряжениями, приложенными к конденсаторам. Итак, пусть у нас по-прежнему имеется три параллельно соединенных конденсатора с емкостями С1, С2 и С3. К ним приложено некоторое переменное напряжение с комплексной амплитудой . Из-за этого приложенного напряжения через конденсаторы будут течь некоторые переменные токи с комплексными амплитудами . Для наглядности давайте нарисуем картинку, на которой будут все фигурировать все эти величины. Она представлена на рисунке 2.
Рисунок 2 – Ищем токи через конденсаторы
Прежде всего надо понять, как связаны токи с суммарным током источника. А связаны они, господа, все по тому же самому первому закону Кирхгофа, с которым мы уже знакомились в отдельной статье. Да, тогда мы его рассматривали в контексте постоянного тока. Но, оказывается, первый закон Кирхгофа остается верным и в случае переменного тока! Просто в этом случае надо использовать комплексные амплитуды токов. Итак, суммарный ток трех параллельно соединенных конденсаторов связан с общим током вот так
То есть общий ток фактически просто разделяется между тремя конденсаторами, тогда как суммарная его величина остается той же самой. Важно помнить еще одну важную вещь – частота тока и его фаза будет одна и та же для всех трех конденсаторов. Точно такая же частота и фаза будет и у суммарного тока I. Таким образом, различаться они будут только лишь амплитудой, которая будет у каждого конденсатора своя. Как же найти эти самые амплитуды токов? Очень просто! В статье про сопротивление конденсатора мы связали между собой ток через конденсатор и напряжение на конденсаторе через сопротивление конденсатора. Сопротивление конденсатора мы легко можем посчитать, зная его емкость и частоту протекающего через него тока (помним, что для разной частоты конденсатор имеет разное сопротивление) по общей формуле:
Воспользовавшись этой замечательной формулой, мы можем найти сопротивление каждого конденсаторы:
Комплексная амплитуда тока связана с комплексной амплитудой напряжения по закону Ома для сетей переменного тока (более подробно про это мы говорили в предыдущей статье):
Воспользовавшись этой формулой, мы легко находим ток через каждый из трех параллельно соединенных конденсаторов:
Общий ток в цепи, который втекает в узел А и вытекает потом из узла В, очевидно, равен
На всякий случай напомню еще раз, что это получилось на основании первого закона Кирхгофа. Заметьте, господа, один важный факт – чем больше емкость конденсатора, тем меньше его сопротивление и тем большая часть тока будет течь через него.
Давайте представим общий ток через три параллельно соединенных конденсатора как отношение приложенного к ним напряжения и некоторого эквивалентного общего сопротивления Zc∑ (которое нам пока неизвестно, но которое мы потом найдем) трех параллельно включенных конденсаторов:
Сокращая левую и правую части на U, получаем
Таким образом, получаем важный вывод: при параллельном соединении конденсаторов обратное эквивалентное сопротивление равно сумме обратных сопротивлений отдельных конденсаторов. Если вы помните, то точно такой же вывод мы получили и при параллельном соединении резисторов.
А что происходит с емкостью? Какая будет общая емкость у системы из трех параллельно соединенных конденсаторов? Можно ли это как-то найти? Безусловно, можно! И, более того, мы почти это сделали. Давайте в нашу последнюю формулу подставим расшифровку сопротивлений конденсаторов. Тогда у нас получится примерна такая запись
После элементарных математических преобразований, доступных даже пятикласснику, получаем, что
Это наш очередной чрезвычайной важный вывод: суммарная емкость системы из нескольких параллельно соединенных конденсаторов равна сумме емкостей отдельных конденсаторов.
Итак, мы рассмотрели основные моменты, касающиеся параллельного соединения конденсаторов. Давайте в сжатой форме резюмируем их все:
- Напряжение на всех трех параллельно соединенных конденсаторах одно и то же (по амплитуде, фазе и частоте);
- Амплитуда тока в цепи, содержащей параллельно соединенные конденсаторы, равна сумме амплитуд токов через отдельные конденсаторы. Чем больше емкость конденсатора, тем больше амплитуда тока через него. Фазы и частоты токов на всех конденсаторов одни и те же;
- При параллельном соединении конденсаторов обратное эквивалентное сопротивление равно сумме обратных сопротивлений отдельных конденсаторов;
- Суммарная емкость параллельно соединенных конденсаторов равна сумме емкостей всех конденсаторов.
Господа, если вы запомните и поймете эти четыре пункта, то, можно сказать, статью я писал не зря.
А теперь давайте для закрепления материала попробуем решить какую-нибудь задачу на параллельное соединение конденсаторов. Потому что, весьма вероятно, если вы ничего не слышали раньше про параллельное соединение конденсаторов, то все написанное выше может восприниматься просто как набор абстрактных буковок, которые не очень понятно как применять на практике. Поэтому, на мой взгляд, наличие приближенных к практике задач является неотъемлемой частью образовательного процесса. Итак, задача.
Допустим, у нас есть три параллельно соединенных конденсаторов с емкостями С1=1 мкФ, С2=4,7 мкФ и С3=22 мкФ. К ним приложено переменное синусоидальное напряжение с амплитудой Umax=50 В и частотой f=1 кГц. Требуется определить
а) напряжение на каждом из конденсаторов;
б) ток через каждый конденсатор и суммарный ток в цепи;
в) сопротивление каждого конденсатора переменному току и общее сопротивление;
г) общую емкость такой системы.
Начнем с напряжения. Мы помним, что на всех конденсаторах напряжение у нас одно и то же – то есть синусоидальное с частотой f=1 кГц и амплитудой Umax=50 В. Предположим, что оно изменяется по синусоидальному закону. Тогда можно записать следующее
Вот мы и ответили на первый вопрос задачи. Осциллограмма напряжения на наших конденсаторах приведена на рисунке 3.
Рисунок 3 – Осциллограмма напряжения на конденсаторах
Дальше, пользуясь общими формулами для сопротивления конденсатора, посчитаем сопротивление каждого конденсатора току с частотой f=1 кГц:
Да, мы видим, что сопротивления у нас получились не только комплексные, но еще и со знаком минус. Однако вас это не должно смущать, господа. Это значит только то, что ток через конденсатор и напряжение на конденсаторе сдвинуты по фазе друг относительно друга, причем ток опережает напряжение. Да, мнимая единичка показывает тут только фазовый сдвиг и ничего больше. Для расчета амплитуды тока нам потребуется только модуль этого комплексного числа. Про все это говорилось уже в прошлых двух статьях (раз и два). Возможно, это не совсем очевидно и требуется какая-либо наглядная иллюстрация этого дела. Это можно сделать на тригонометрическом круге и, надеюсь, немного позже, я подготовлю отдельную статью, посвященную этому, либо вы можете сами придумать, как это показать наглядно, пользуясь данными из моей статьи про комплексные числа в электротехнике. Теперь ничего не мешает найти обратное общее сопротивление:
Находим общее сопротивление трех наших параллельно соединенных конденсаторов
Следует помнить, что это сопротивление верно исключительно для частоты 1 кГц. Для других частот значение сопротивления, очевидно, будет другое.
Следующим шагом рассчитаем амплитуды токов через каждый конденсатор. В расчете будем использовать модули сопротивлений (отбросим мнимую единицу), помня при этом, что сдвиг фаз между током и напряжением будет 90 градусов (то есть, если напряжение у нас меняется по закону синуса, то ток будет меняться по закону косинуса). Можно вести расчет и с комплексными числами, используя комплексные амплитуды тока и напряжения, но, на мой взгляд, в данной задаче проще просто учесть потом фазовые соотношения. Итак, амплитуды токов равны
Суммарная амплитуда тока в цепи, очевидно, равна
Мы можем себе позволить вот так вот складывать амлитуды сигналов, потому что у всех токов через параллельно соединенные конденсаторы у нас одна и та же частота и фаза. В случае невыполнения этого требования вот так вот просто взять и сложить нельзя.
Теперь, помня про фазовые соотношения, нам никто не мешает записать законы изменения тока через каждый конденсатор
И суммарный ток в цепи
Осциллограммы токов через конденсаторы приведены на рисунке 4.
Рисунок 4 – Осциллограммы токов через конденсаторы
Ну и в завершении задачи самое простое – найдем общую емкость системы как сумму емкостей:
Кстати, эту емкость вполне можно использовать для расчета суммарного сопротивления трех параллельно соединенных конденсаторов. В качестве упражнения читателю предлагается самому в этом убедиться .
В заключение хотелось бы выяснить один, возможно, самый важный вопрос: а зачем вообще нужно на практике соединять конденсаторы параллельно? Что это дает? Какие возможности нам открывает? Ниже по пунктам я обозначил основные моменты:
- Параллельное соединение конденсаторов дает увеличение емкости системы. Пожалуй, это самый основной и главный пункт. Например, в нашей системе нужна емкость не менее 1000 мкФ, а в нашем распоряжении только конденсаторы на 220 мкФ. Что делать? Правильно, взять этих конденсаторов штук пять и получить требуемую емкость.
- Конденсаторы часто используют для сглаживания пульсаций напряжения. Бывает, что в этом случае через конденсатор текут весьма значительные импульсные токи (например, в импульсных источниках питания). Каждый конденсатор может выдержать отнюдь не бесконечно большую величину импульсного тока. Таким образом, если величина импульсного тока в системе превышает максимально допустимый ток для данного типа конденсаторов, то их соединяют несколько штук параллельно. При этом ток распределяется между этими конденсаторами.
- Существует такое понятие, как «резонанс конденсатора». Подробно о нем мы погорим позднее. Если быть кратким, то суть явления заключается в том, что на высоких частотах, начиная с некоторой резонансной частоты, из-за паразитных индуктивностей конденсатор перестает быть конденсатором и начинает вести себя как дроссель. У разных конденсаторов эта резонансная частота различна: у кого-то она больше, у кого-то меньше. Так вот, когда нужна фильтрация сигнала в широком диапазоне частот, применяют параллельное соединение конденсаторов с разными резонансными частотами. Например, соединяют параллельно конденсаторы с емкостью 0,1 мкФ, 10 нФ, 100 пФ, 22 пФ. Такое соединение даст эффективное подавление помех в широком диапазоне. Более подробно обсудим это интересное явление в другой раз.
Ну а мы на этом заканчиваем, господа. Спасибо за внимание и до новых встреч!
Вступайте в нашу группу Вконтакте
Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.
Social button for Joomla
Последовательное соединение
Последовательное соединение конденсаторов – это их подключение непосредственно друг за другом без разветвлений проводника. От источника напряжения заряды поступают на обкладки первого и последнего в цепи конденсаторов.
В силу электростатической индукции на внутренних обкладках смежных конденсаторов происходит выравнивание заряда на электрически соединённых обкладках смежных конденсаторов, поэтому на них появляются равные по величине и обратные по знаку электрические заряды.
При таком соединении электрические заряды на обкладках отдельных кондёров по величине равны:
Общее напряжение для всей цепи:
Очевидно, что напряжение между проводниками для каждого конденсатора зависит от накопленного заряда и ёмкости, т.е.:
Поэтому эквивалентная ёмкость последовательной цепи равна:
Отсюда следует, что величина, обратная общей емкости, равна сумме величин, обратных емкостям отдельных конденсаторов:
Смешанное соединение
Смешанным соединение конденсаторов называют такое соединение, при котором присутствует соединение последовательное и параллельное одновременно. Чтобы более подробно разобраться , давайте рассмотрим это соединение на примере :
На рисунке видно ,что соединены два конденсатора последовательно вверху и внизу и два параллельно. Можно вывести формулу из выше описанных соединении:
Основой любой радиотехники является конденсатор, он используется в самых разнообразных схемах-это и источники питания и применение для аналоговых сигналов хранения данных , а также в телекоммуникационных связи для регулирования частоты.
Параллельное и последовательное соединение конденсаторов — Всё о электрике
Поведение, характеристики радиоэлементов зависят от вида протекающего тока (постоянный, переменный), от способа их подключения.
Мнение эксперта
It-Technology, Cпециалист по электроэнергетике и электронике
Задавайте вопросы «Специалисту по модернизации систем энергогенерации»
Формула расчета последовательного соединения конденсатора Но если в параллельном или последовательном соединении конденсаторов еще есть хоть какая-то логика, то кому вообще нужно смешанное. Спрашивайте, я на связи!
Тема: Нагрузочные резисторы параллельно основным конденсаторам БП
Опции темы
В некоторых схемах заводских УМЗЧ не раз встречал высокоомные резисторы, стоящие параллельно основным банкам БП. Вопрос, имеет ли смысл? Или это тупо лишняя грелка в усилителе. И если да, то какой номинал нужен для обычного трансформаторного БП +-55В, и емкостями по 30000мкф в плечо.
pyos
, понял, спасибо за ответ! Только 0.25 наверное не серьезно как то ) Я так то не жадный, может двухваттные воткнуть? )
А нафига? Не, если у тебя есть пара-другая лишних двухваттников, то ради Б-га. Допустимый номинал в таком случае можно соответственно уменьшить.
это делается по двум причинам. первая что бы заряд на банках разряжался после выключения, что бы во время ремонта не долбануло. о второй причине писал Константин Мусатов, но это применительно только если УТ питается раздельно и когда неактивное плечо остается полностью без нагрузки
Просто думаю так будет лучше в плане того, что никакой остаточной напряги в схеме не будет, и чтобы не было заметных всплесков напруги без нагрузки на блок. Хотя может я и не прав, и тут не надо оно. Поэтому и интересуюсь, что сам не очень то понимаю )
Ka4aN
, во как! Даже не знал что стабы как и усилки в классе А гоняться могут. Только не совсем понятно зачем? Стаб же он всегда напругу четко держит, зачем его под нагрузкой зря держать? Лишнее потребление и тепловыделение.
Мы говорим о стабилизаторах как источниках питания? Что то это выше моего понимания, зачем держать стабильный источник питания под нагрузкой. Ну да ладно, это не мой уровень однозначно ))
Минимальный ток нагрузки так-то и в даташите указан.
Просто когда идет речь о безкомпромиссной борьбе с помехами, безкомпромисной точности напряжения на выходе этого стабилизатора (не такой уж он и стабильный по умолчанию), всё начинает иметь значение. И резисторы в т.ч. Хотя, пожалуй, Вам действительно пока что не стоит забивать такой ерундой голову. Я просто привел для примера, в тему топика.
Вы правы ) Но тем не менее теперь я понял. В гонке за идеальными цифирями все средства хороши )
В смысле? Как не обеспечивает, если ты нагружаешь этот стаб на некую нагрузку, которая может меняться хоть до плюс бесконечности и параллельно ей ставишь ещё одну, через которую стабильно будет протекать минимально необходимый для стаба ток?
А кто это вот тут справа от треугольника нарисован:
Вот когда он тупить начинает (слишком маленький/слишком большой ток), тогда и начинаются выбросы, т.к. ОУ рассчитан на определённую скорость выходника.
на этом лучше и закрыть, т.к. многих тут выворачивает от «знайкинства». тут можно прочитать неведомое число «советов» как сделать «идеальное». но не всему надо верить.
Источник