Соединения резисторов, конденсаторов и индуктивностей

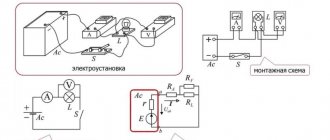
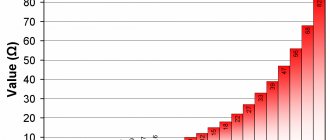
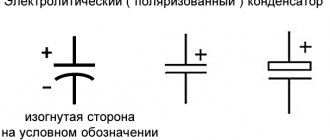
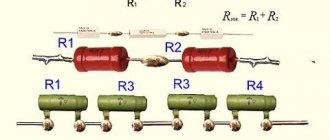
ОБЩАЯ ЭЛЕКТРОТЕХНИКА И ЭЛЕКТРОНИКА. ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ

Катушка индуктивности

— является пассивным компонентом электронных схем, основное предназначение которой является сохранение энергии в виде магнитного поля. Свойство катушки индуктивности чем-то схоже с конденсатором, который хранит энергию в виде электрического поля.

Индуктивность (измеряется в Генри) — это эффект возникновения магнитного поля вокруг проводника с током. Ток, протекающий через катушку индуктивности, создает магнитное поле, которое имеет связь с электродвижущей силой (ЭДС) оказывающее противодействие приложенному напряжению.

Возникающая противодействующая сила (ЭДС) противостоит изменению переменного напряжения и силе тока в катушке индуктивности. Это свойство индуктивной катушки называется индуктивным сопротивлением. Следует отметить, что индуктивное сопротивление находится в противофазе к емкостному реактивному сопротивлению конденсатора в цепи переменного тока. Путем увеличения числа витков можно повысить индуктивность самой катушки.

Параллельное соединение конденсатора

⇐ ПредыдущаяСтр 6 из 7Следующая ⇒

И катушки индуктивности.

Понятие о резонансе токов

Когда к цепи (рис. 8.1) с параллельным соединением конденсатора и катушки индуктивности подается переменное синусоидальное напряжение U, одно и то же напряжение приложено к обоим элементам цепи.

Рис. 8.1

Общий ток цепи I разветвляется на ток в конденсаторе IC (емкостная составляющая общего тока) и ток в катушке IL (индуктивная составляющая общего тока), причем ток IL отстает от напряжения U на 90°, а IC опережает на 90°.

Токи IC и IL имеют противоположные фазы (180°) и в зависимости от их величин уравновешивают друг друга полностью или частично. Они могут быть представлены с помощью векторных диаграмм токов.

Когда IC= IL и общий ток цепи равен нулю, имеет место резонанс токов

(векторная диаграмма рис. 8.2)

Рис. 8.2 Рис. 8.3 Рис. 8.4

Когда IC > IL, т.е. преобладает ток конденсатора, общий ток цепи I является по характеру емкостным и опережает напряжение U на 90º (рис. 8.3).

Когда IC < IL, т.е. преобладает ток катушки, общий ток цепи I является индуктивным и отстает от напряжения U на 90° (рис. 8.4).

Эти рассуждения проведены в пренебрежении потерями активной мощности в конденсаторе и катушке.

При резонансе токов реактивная проводимость цепи В = BL — BC равна нулю. Резонансная частота определяется из уравнения:

откуда, так же, как и при резонансе напряжений,

Полная проводимость при резонансе токов оказывается близкой к нулю. Остается некомпенсированной лишь небольшая активная

проводимость, обусловленная активным сопротивлением катушки и несовершенной изоляцией конденсатора. Поэтому ток в неразветвленной части цепи имеет минимальное значение, тогда как токи IL и IC могут превышать его в десятки раз.

Экспериментальная часть

Задание

Для цепи с параллельным соединением конденсатора и катушки индуктивности измерьте действующие значения напряжения U и токов I, IC и IL при Постройте векторные диаграммы.

Порядок выполнения работы

• Соберите цепь согласно схеме (рис. 8.5), подсоедините регулируемый источник синусоидального напряжения и установите его параметры: U= 7 В, f = 500 Гц. В качестве индуктивности с малым активным сопротивлением используйте катушку трансформатора 300 витков, вставив между подковами разъемного сердечника полоски бумаги в один слой (немагнитныйзазор).

Рис. 8.5

• Изменяя частоту приложенного напряжения, добейтесь резонанса по минимальному току I. Для точной настройки поддерживайте неизменным напряжение на входе цепи. При измерениях виртуальными приборами резонанс настраивается по переходу через ноль угла сдвига фаз между входным током и напряжением. Тогда необязательно поддерживать неизменным напряжение на входе цепи.

• Произведите измерения и запишите результаты измерений в таблицу 8.1 при f = f0, f1≈0,75f0 и f2 ≈l,25f0.

Таблица 8.1

Постройте в одинаковом масштабе векторные диаграммы на рисунке 8.6 для каждого из рассмотренных случаев.

Рис. 8.6

Контрольные вопросы:

1. Почему резонанс в параллельной цепи называется резонансом токов?
2. Какими способами можно добиться резонанса токов?
3. Чему равна резонансная частота?
4. Обязательно ли уменьшится общий ток, если параллельно катушке включить конденсатор?
5. Каково применение резонанса токов?
6. Какой вид имеют резонансные кривые?
7. Каковы условия резонанса токов?
8. Изобразите векторные диаграммы для различных режимов работы исследуемой электрической цепи при
9. Какова особенность токов в ветвях при резонансе токов?
10. Каким образом можно определить на опыте и зафиксировать резонанс токов?
11. Как изменяется вид резонансных кривых в случае резонанса токов при увеличении активного сопротивления исследуемой цепи?
12. с какой целью стремятся увеличить коэффициент мощности ? Назовите способы его повышения.

Лабораторная работа №9 Трехфазная нагрузка, соединенная по схеме «звезда»

У реальных трехфазных генераторов обмотки часто имеют одну общую точку, в которой соединяются концы обмоток X,Y,Z. Такую схему соединения называют звездой,а общую точку обмоток – нулевой точкой или нейтралью генератора. С приемником энергии генератор соединяется тремя или четырьмя проводами. Три из них, называемые линейными,присоединяют к началам обмоток (зажимы А,В,С), а четвертый – нулевой или нейтральный – присоединяют к нулевой точке. Применяются системы и без нейтрального провода.

Напряжениямежду линейнымипроводами(т.е. между началами обмоток генераторов)принято называть линейными и обозначать, ,причем порядок индексов указывает положительное направление напряжения во внешней цепи. Напряжения между линейными и нейтральными проводами (т.е. между началами и концами обмоток) называют фазными напряжениями иобозначают, Фазное напряжение отличается от фазной э.д.с. на величину падения в обмотке генератора. Установим соотношение между линейными и фазными напряжениями при соединении обмоток генератора звездой. Мгновенные значения линейных и фазных напряжений равны разностям мгновенных значений потенциалов начал и концов соответствующих обмоток:

Так как концы обмоток соединены в одну точку, то потенциалы

,

и мгновенное линейное напряжение между точками А и В

Аналогично линейные напряжения

Таким образом, мгновенные значения линейных напряжений равны алгебраическим разностям мгновенных значений соответствующих фазных напряжений.

Если напряжения выразить комплексными величинами, то комплексное линейное напряжение определяется как разность соответствующих комплексных фазных напряжений:

.

Точно так же векторы линейных напряжений равны разностям векторов фазных напряжений. Векторы линейных напряжений всегда образуют замкнутый треугольник, так как сумма тождественно равна нулю. Это станет очевидным, если векторы линейных напряжений переместить параллельно самим себе.

Рассматривая диаграммы, мы видим, что и векторы двух соседних фазных напряжений вместе с вектором соответствующего линейного напряжения образуют замкнутый треугольник. При симметричной системе напряжений этот треугольник равнобедренный, его углы равны 30, 30 и 120. Следовательно:

а) между действующими значениями фазных и линейных напряжений существует отношение

или

т. е. линейное напряжениев раза больше фазного;

б) векторная диаграмма симметричных линейных напряжений сдвинута на 30 градусов в сторону вращения векторов относительно диаграммы фазных напряжений.

Если нагрузки (приемники) соединены в трехфазную цепь по схеме «звезда» с нулевым проводом (рис. 9.1), то к сопротивлениям нагрузки приложены фазные напряжения.

Линейные токи равны фазным и определяются по закону Ома:

При симметричных напряжениях UA, UB , UC и одинаковых сопротивлениях RA=

RB = RC = R токи IA, IB , IC также симметричны и их векторная сумма (In) равна нулю. Тогда

Если же сопротивления фаз нагрузки неодинаковы, то через нулевой провод протекает некоторый ток IN=0. Это поясняется на векторных диаграммах (рис. 9.2). а) симметричная нагрузка б) несимметричная нагрузка

Мощность трёхфазной нагрузки складывается из мощностей фаз: ∑Р = РA + РB + РC Когда нагрузка симметричная и чисто резистивная, имеем

При смешанной (активно-индуктивной или активно-емкостной) нагрузке

Активная мощность

Реактивная мощность

Полная мощность

Экспериментальная часть

Задание

Для трехфазной цепи с соединением «звезда» при симметричной и несимметричной нагрузках измерьте с помощью мультиметра действующие значения токов IЛ и IN, а также напряжений UЛ и UФ, вычислите мощности РФ и ∑PФ , простройте векторные диаграммы.

⇐ Предыдущая6Следующая ⇒

Рекомендуемые страницы:

Накопленная энергия в индуктивности

Как известно магнитное поле обладает энергией. Аналогично тому, как в полностью заряженном конденсаторе существует запас электрической энергии, в индуктивной катушке, по обмотке которой течет ток, тоже существует запас — только уже магнитной энергии.

Энергия, запасенная в катушке индуктивности равна затраченной энергии необходимой для обеспечения протекания тока I в противодействии ЭДС. Величина запасенной энергии в индуктивности можно рассчитать по следующей формуле:

где L — индуктивность, I — ток, протекающий через катушку индуктивности.

Гидравлическая модель

Работу катушки индуктивности можно сравнить с работой гидротурбины в потоке воды. Поток воды, направленный сквозь еще не раскрученную турбину, будет ощущать сопротивление до того момента, пока турбина полностью не раскрутится.

Далее турбина, имеющая определенную степень инерции, вращаясь в равномерном потоке, практически не оказывая влияния на скорость течения воды. В случае же если данный поток резко остановить, то турбина по инерции все еще будет вращаться, создавая движение воды. И чем выше инерция данной турбины, тем больше она будет оказывать сопротивление изменению потока.

Также и индуктивная катушка сопротивляется изменению электрического тока протекающего через неё.

Индуктивность в электрических цепях

В то время как конденсатор оказывает сопротивление изменению переменного напряжения, индуктивность же сопротивляется переменному тока. Идеальная индуктивность не будет оказывать сопротивление постоянному току, однако, в реальности все индуктивные катушки сами по себе обладают определенным сопротивлением.

В целом, отношение между изменяющимися во времени напряжением V(t) проходящим через катушку с индуктивностью L и изменяющимся во времени током I(t), проходящим через нее можно представить в виде дифференциального уравнения следующего вида:

Когда переменный синусоидальной ток (АС) протекает через катушку индуктивности, возникает синусоидальное переменное напряжение (ЭДС). Амплитуда ЭДС зависит от амплитуды тока и частоте синусоиды, которую можно выразить следующим уравнением:

где ω является угловой частотой резонансной частоты F:

Причем, фаза тока отстает от напряжения на 90 градусов. В конденсаторе же все наоборот, там ток опережает напряжение на 90 градусов. Когда индуктивная катушка соединена с конденсатором (последовательно либо параллельно), то образуется LC цепь, работающая на определенной резонансной частоте.

Индуктивное сопротивление ХL определяется по формуле:

где ХL — индуктивное сопротивление, ω — угловая частота, F — частота в герцах, и L индуктивность в генри.

Индуктивное сопротивление — это положительная составляющая импеданса. Оно измеряется в омах. Импеданс катушки индуктивности (индуктивное сопротивление) вычисляется по формуле:

Последовательное соединение элементов цепи при переменном напряжении

Начнём с последовательного соединения сопротивления R, индуктивности L и ёмкости C и рассмотрим воздействие на неё переменного напряжения с частотой ω.

В данной цепи входное переменное напряжение U в соответствии со вторым законом Кирхгофа будет равно алгебраической сумме переменных напряжений на отдельных элементах

где UR, UL, UC – напряжение на элементах цепи, сопротивлении R, индуктивности L и ёмкости С, соответственно,

Im­ – амплитудное значение переменного тока.

Графическое изображение напряжений и токов на последовательно соединённых элементах цепи представлено ниже

Итоговое выражение является тригонометрической формой записи второго закона Кирхгофа для мгновенных напряжений и его можно переписать в виде

где R – активное сопротивление,

Х – реактивное сопротивление.

Значение активного сопротивления R всегда только положительно, а реактивное сопротивление Х может принимать, как положительное значение Х > 0, тогда оно имеет индуктивный характер, так и отрицательное значение X < 0, в этом случае реактивное сопротивление имеет ёмкостный характер.

В случае же нулевого значения реактивного сопротивления, имеет место резонанс напряжений

В этом случае сопротивление цепи представлено только активной нагрузкой R, а следовательно сдвиг фаз между напряжением и током будет нулевым.

При расчётах нас интересует не столько ток и напряжение на отдельных элементах, сколько ток и напряжение всей цепи. Для этого продолжим преобразовывать напряжение

где Z – полное сопротивление цепи,

ψ – разность фаз между напряжением и током.

Таким образом, амплитудное значение напряжения Um и амплитудное значение тока Im связаны между собой следующим соотношением

где Um­ – амплитудное значение переменного напряжения,

Im­ – амплитудное значение переменного тока,

Z – полное сопротивление цепи.

Схемы соединения катушек индуктивностей

Параллельное соединение индуктивностей

Напряжение на каждой из катушек индуктивностей, соединенных параллельно, одинаково. Эквивалентную (общую) индуктивность параллельно соединенных катушек можно определить по формуле:

Последовательное соединение индуктивностей

Ток, протекающий через катушки индуктивности соединенных последовательно, одинаков, но напряжение на каждой катушке индуктивности отличается. Сумма разностей потенциалов (напряжений) равна общему напряжению. Общая индуктивность последовательно соединенных катушек можно высчитать по формуле:

Эти уравнения справедливы при условии, что магнитное поле каждой из катушек не оказывает влияние на соседние катушки.

Конвертер величин

1 мГн = 0,001 Г. 1 мкГн = 0,000001 = 10⁻⁶ Гн. 1 нГн = 0,000000001 = 10⁻⁹ Гн. 1 пГн = 0,000000000001 = 10⁻¹² Г. Подробнее о единицах измерения индуктивности.

Индуктивность характеризует способность электрического проводника преобразовывать электрический ток в изменение электрического потенциала в данном проводнике (самоиндукция) и в расположенных рядом проводниках (взаимоиндукция). Индуктивность обычно обозначается символом L в честь русского физика немецкого происхождения Эмилия Христиановича Ленца (Heinrich Lenz).

По определению самоиндукции напряжение v(t)

и ток
i(t)
в катушке индуктивности связаны выражением

На всех соединенных параллельно катушках индуктивности имеется одно и то же напряжение V

. В соответствии с правилом Кирхгофа для тока общий ток
I
равен сумме токов, протекающих через отдельные катушки:

Общая индуктивность Leq соединенных параллельно трех катушек индуктивности, расположенных далеко друг от друга и не имеющих общего магнитного поля равна величине, обратной сумме величин, обратных их индуктивностям:

Или для n

несвязанных катушек индуктивности:

Эта формула для L

eq используется для расчетов в этом калькуляторе. Например, общая индуктивность трех катушек индуктивности 10, 15 and 20 мкГн, соединенных параллельно, будет равна

мкГн.

Отметим, что если одна или несколько величин индуктивности равны нулю, то Leq стремится к нулю. Представьте себе очень короткий прямой проводник, шунтирующий катушку индуктивности — он и будет иметь почти нулевую индуктивность. Отметим также, что невозможно создать схему с нулевой индуктивностью. Если параллельно соединены только две катушки индуктивности, имеем:

или

Эквивалентная индуктивность n

одинаковых соединенных параллельно катушек индуктивности
L
равна

Отметим, что формула для расчета общей индуктивности нескольких катушек индуктивности, соединенных параллельно, используется и для расчета сопротивления группы резисторов, соединенных параллельно.

Отметим также, что для группы из любого количества соединенных параллельно катушек индуктивности эквивалентная индуктивность всегда будет меньше самой малой индуктивности в группе катушек индуктивности, а добавление еще одной катушки всегда будет уменьшать эквивалентную индуктивность группы.

Если индукторы расположены в магнитном поле друг друга, эти формулы работать не будут из-за явления взаимоиндукции (взаимной индукции)

, которое рассматривается в нашем калькуляторе взаимной индукции. Эффект взаимоиндукции может уменьшить или увеличить общую индуктивность катушек в зависимости от того как работает магнитная связь между катушками. Величина взаимной индукции зависит от расстояния между катушками и их ориентации. При этом взаимоиндукция может увеличивать или уменьшать общую индуктивность.

Если несколько катушек индуктивности соединены последовательно

, их эквивалентная индуктивность определяется простым сложением индуктивностей отдельных катушек.

Для n

соединенных последовательно катушек индуктивности имеем

Возможно, вы уже заметили, что катушки индуктивности ведут себя точно так же, как резисторы: если катушки соединены последовательно, их эквивалентные индуктивности всегда будет выше, чем индуктивности отдельных катушек, соединенных последовательно, а при параллельном соединении эквивалентная индуктивность всегда будет меньше индуктивностей отдельных катушек.

Зачем соединять катушки последовательно, если можно просто намотать большую катушку индуктивности? Вот один из примеров.

В микроэлектронике для реализации довольно больших индуктивностей на единицу площади интегральной микросхемы используется комбинирование спиральных катушек в нескольких слоях металлизации. Для этой цели используется многослойная пакетная конфигурация катушек индуктивности. Несколько слоев металлизации со спиральными катушками располагают точно один над другим. Катушки соединяют последовательно, чтобы индуктивности складывались для получения одной большой катушки индуктивности. Без такого пакетного расположения при использовании планарной технологии было бы невозможно создать большие индуктивности. Благодаря такому пакетному расположению коэффициент связи катушек k

≈ 1.

В этом калькуляторе мы рассматриваем только идеальные катушки индуктивности. Однако мы живем в реальном мире, где реальные катушки обладают как активным сопротивлением, так и емкостью. В другом калькуляторе мы рассмотрим характеристики неидеальных катушек индуктивности, обладающих сопротивлением, которые описываются эквивалентной схемой из последовательно соединенных индуктивности и сопротивления, в частности их временные характеристики.

Автор статьи: Анатолий Золотков

Добротность катушки индуктивности

На практике катушка индуктивности имеет последовательное сопротивление, созданное медной обмоткой самой катушки. Это последовательное сопротивление преобразует протекающий через катушку электрический ток в тепло, что приводит к потере качества индукции, то есть добротности. Добротность является отношением индуктивности к сопротивлению.

Добротность катушки индуктивности может быть найдена через следующую формулу:

где R является собственным сопротивлением обмотки.

Согласное и встречное включение индуктивностей

Выводы двух индуктивно связанных катушек, относительно которых токи направлены одинаково и направления создаваемых ими потоков самоиндукции и взаимной индукции в каждой катушке совпадают, называют одноимёнными, а включение катушек – согласным. Иначе говоря, одноимённые зажимы двух катушек обладают той особенностью, что подведение к одной из них возрастающего тока приводит к повышению потенциала на одноимённом зажиме другой катушки.

Если же потоки будут направлены встречно, то выводы катушек, относительно которых направления токов совпадают, называют разноимёнными, а включение катушек – встречным. На принципиальных электрических схемах одноимённые выводы обозначают каким-либо одинаковым знаком, например, «звёздочкой» (*), точкой или другим.

Рис. 12.2. Согласное (а, в) и встречное (б, г) включение катушек индуктивности

В связи с введением понятия одноимённых выводов при вычерчивании электрических схем нет необходимости показывать намотку витков катушек индуктивности, а достаточно разметить на схеме их одноимённые зажимы и выбранные положительные направления токов (рис. 12.2).

Комплексная форма расчёта цепей с взаимными индуктивностями

Соединим две индуктивно связанные катушки последовательно так, что­бы полный магнитный поток каждой из катушек увеличился, то есть включим катушки согласно (рис. 12.2, в).

На основании закона Фарадея ЭДС самоиндукции первой катушки в комплексной форме записи равна

Электродвижущая сила взаимоиндукции при согласном включении катушек будет иметь такой же знак, как и , то есть

Подобные соотношения имеют место и для второй индуктивности.

Учитывая, что , составим уравнение для нахождения напряжения в случае согласованного включения катушек:

Так как , то получим

где .

При последовательном встречном включении катушек индуктивности (рис. 12.2, г) уравнение напряжения на выводах схемы будет равно:

где .

На рис. 12.3 приведены топографические векторные диаграммы для согласного и встречного последовательного соединения двух катушек индуктивности.

Два последних уравнения указывают способ нахождения величины вза­имоиндукции . Для этого надо измерить реактивные составляющие полных сопротивлений при согласном и встречном включении индуктивностей и вычесть их

Рис. 12.3. Векторные диаграммы последовательно включенных согласно (а) и встречно (б) индуктивно связанных катушек

Отсюда получаем выражение

которое позволяет по экспериментальным данным рассчитать величину взаимной индукции.

Выводы двух индуктивно связанных катушек, относительно которых токи направлены одинаково и направления создаваемых ими потоков самоиндукции и взаимной индукции в каждой катушке совпадают, называют одноимёнными, а включение катушек – согласным. Иначе говоря, одноимённые зажимы двух катушек обладают той особенностью, что подведение к одной из них возрастающего тока приводит к повышению потенциала на одноимённом зажиме другой катушки.

Если же потоки будут направлены встречно, то выводы катушек, относительно которых направления токов совпадают, называют разноимёнными, а включение катушек – встречным. На принципиальных электрических схемах одноимённые выводы обозначают каким-либо одинаковым знаком, например, «звёздочкой» (*), точкой или другим.

Рис. 12.2. Согласное (а, в) и встречное (б, г) включение катушек индуктивности

В связи с введением понятия одноимённых выводов при вычерчивании электрических схем нет необходимости показывать намотку витков катушек индуктивности, а достаточно разметить на схеме их одноимённые зажимы и выбранные положительные направления токов (рис. 12.2).

Комплексная форма расчёта цепей с взаимными индуктивностями

Соединим две индуктивно связанные катушки последовательно так, что­бы полный магнитный поток каждой из катушек увеличился, то есть включим катушки согласно (рис. 12.2, в).

На основании закона Фарадея ЭДС самоиндукции первой катушки в комплексной форме записи равна

Электродвижущая сила взаимоиндукции при согласном включении катушек будет иметь такой же знак, как и , то есть

Подобные соотношения имеют место и для второй индуктивности.

Учитывая, что , составим уравнение для нахождения напряжения в случае согласованного включения катушек:

Так как , то получим

где .

При последовательном встречном включении катушек индуктивности (рис. 12.2, г) уравнение напряжения на выводах схемы будет равно:

где .

На рис. 12.3 приведены топографические векторные диаграммы для согласного и встречного последовательного соединения двух катушек индуктивности.

Два последних уравнения указывают способ нахождения величины вза­имоиндукции . Для этого надо измерить реактивные составляющие полных сопротивлений при согласном и встречном включении индуктивностей и вычесть их

Рис. 12.3. Векторные диаграммы последовательно включенных согласно (а) и встречно (б) индуктивно связанных катушек

Отсюда получаем выражение

которое позволяет по экспериментальным данным рассчитать величину взаимной индукции.

Катушка индуктивности. Формула индуктивности

Базовая формула индуктивности катушки

• L = индуктивность в генри
• μ 0 = проницаемость свободного пространства = 4π x 10 -7 Гн / м
• μ г = относительная проницаемость материала сердечника
• N = число витков
• A = Площадь поперечного сечения катушки в квадратных метрах (м 2 )
• l = длина катушки в метрах (м)

Индуктивность прямого проводника

• L = индуктивность в нГн
• l = длина проводника
• d = диаметр проводника в тех же единицах, что и l

Индуктивность катушки с воздушным сердечником

• L = индуктивность в мкГн
• r = внешний радиус катушки
• l = длина катушки
• N = число витков

Индуктивность многослойной катушки с воздушным сердечником

• L = индуктивность в мкГн
• r = средний радиус катушки
• l = длина катушки
• N = число витков
• d = глубина катушки

Индуктивность плоской катушки

• L = индуктивность в мкГн
• r = средний радиус катушки
• N = число витков
• d = глубина катушки

Конструкция катушки индуктивности

Катушка индуктивности представляет собой обмотку из проводящего материала, как правило, медной проволоки, намотанной вокруг либо железосодержащего сердечника, либо вообще без сердечника.

Применение в качестве сердечника материалов с высокой магнитной проницаемостью, более высокой чем воздух, способствует удержанию магнитного поля вблизи катушки, тем самым увеличивая ее индуктивность. Индуктивные катушки бывают разных форм и размеров.

Большинство изготавливаются путем намотки эмалированного медного провода поверх ферритового сердечника.

Некоторые индуктивные катушки имеют регулируемый сердечник, при помощи которого обеспечивается изменение индуктивности.

Миниатюрные катушки могут быть вытравлены непосредственно на печатной плате в виде спирали. Индуктивности с малым значением могут быть расположены в микросхемах с использованием тех же технологических процессов, которые используются при создании транзисторов.

Применение катушек индуктивности

Индуктивности широко используются в аналоговых схемах и схемах обработки сигналов. Они в сочетании с конденсаторами и другими радиокомпонентами образуют специальные схемы, которые могут усилить или отфильтровать сигналы определенной частоты.

Катушки индуктивности получили широкое применение начиная от больших катушек индуктивности, таких как дроссели в источниках питания, которые в сочетании с конденсаторами фильтра устраняют остаточные помехи и другие колебания на выходе источника питания, и до столь малых индуктивностей, которые располагаются внутри интегральных микросхем.

Две (или более) катушки индуктивности, которые соединены единым магнитным потоком, образуют трансформатор, являющимся основным компонентом схем работающих с электрической сетью электроснабжения. Эффективность трансформатора возрастает с увеличением частоты напряжения.

По этой причине, в самолетах используется переменное напряжение с частотой 400 герц вместо обычных 50 или 60 герц, что в свою очередь позволяет значительно сэкономить на массе используемых трансформаторов в электроснабжении самолета.

Так же индуктивности используются в качестве устройства для хранения энергии в импульсных стабилизаторах напряжения, в высоковольтных электрических системах передачи электроэнергии для преднамеренного снижения системного напряжения или ограничения ток короткого замыкания.

Расчет катушек индуктивности

Любой проводник с током создает вокруг себя магнитное поле. Отношение магнитного потока этого поля к порождающему его току называется индуктивностью. Индуктивность прямого отрезка проводника невелика и составляет 1…2 мкГн на каждый метр длины в зависимости от диаметра провода (тонкие проводники имеют большую индуктивность). Более точные результаты дает формула

где — длина провода; d — его диаметр. Оба размера надо брать в метрах (под знаком логарифма допустимо в любых, но одинаковых единицах), индуктивность получится в микрогенри. Для облегчения расчетов напомним, что натуральный логарифм любого числа в 2,3 раза больше десятичного логарифма (который можно найти с помощью таблиц, логарифмической линейки или калькулятора), т. е. Inx = 2,3lgx.

Зачем мы дали эту формулу? Поясним примером.

Пусть выводы некоторого радиоэлемента имеют длину 4 см при диаметре 0,4 мм. Сосчитаем их индуктивность:

2,3lg100 = 4,6 и 0,2-0,04-3,6 = 0,03 (округляем).

Итак, индуктивность каждого вывода близка к 0,03 мкГн, а двух выводов — 0,06 мкГн. С емкостью всего 4,5 пФ (а емкость монтажа может быть и больше) такая индуктивность образует колебательный контур, настроенный на частоту 300 МГц, — вспомните формулу Томсона:

f = 1/2π√LC.

Вот почему на УКВ нельзя вести монтаж длинными проводами и оставлять длинные выводы деталей.

Чтобы увеличить индуктивность, проводник сворачивают в кольцо. Магнитный поток внутри кольца возрастает, и индуктивность становится примерно втрое больше:

L = 0,27πD(ln8D/d-2).

Здесь D — диаметр кольца, размерности те же. Дальнейшее увеличение индуктивности происходит при увеличении числа витков, при этом магнитные потоки отдельных витков не только складываются, но и воздействуют на все остальные витки. Поэтому индуктивность возрастает пропорционально квадрату числа витков. Если в катушке N витков, полученную для одного витка индуктивность надо умножить на N2.

Для однослойной цилиндрической катушки с длиной , намного большей диаметра D (рис. 23), индуктивность достаточно точно рассчитывается по формуле

строго выведенной для очень длинного соленоида или тора. Все размерности здесь в системе СИ (метры, Генри), μ0 = 4π·10-7 Гн/м — магнитная константа; S = πD2/4 — площадь поперечного сечения катушки; μ — эффективная магнитная проницаемость магнитопровода. Для незамкнутых магнитопроводов она значительно меньше проницаемости самого материала. Например, для стержня магнитной антенны из феррита марки 600НН (магнитная проницаемость 600) и едва достигает 150. Если магнитопровода нет, μ = 1.

Очень точные результаты эта формула дает для тороидальных катушек, причем l

соответствует длине окружности кольцевого магнитопровода, измеренной по его средней линии. Формула годится и для низкочастотных трансформаторов, намотанных на Ш-образном магнитопроводе (рис. 24).

В этом случае S = ab — площадь сечения магнитопровода, а l

— это средняя длина магнитной силовой линии, показанная на рисунке пунктиром. Для замкнутых магнитопроводов, собранных без зазора, как и для ферритовых колец, и берется равной магнитной проницаемости материала. Малый зазор незначительно снижает μ. Учесть его влияние можно, увеличив длину магнитной силовой линии
l
на величину δμ, где δ — ширина зазора, μ — магнитная проницаемость материала сердечника.

Как видим, от диаметра провода индуктивность практически не зависит. У низкочастотных катушек диаметр провода выбирают исходя из допустимой плотности тока, для медных проводников 2…3 ампера на каждый мм2 сечения проводника. В других случаях, особенно у радиочастотных катушек, стремятся получить минимальное сопротивление проводника, чтобы увеличить добротность (отношение индуктивного сопротивления к активному).

С этой целью надо, казалось бы, увеличивать диаметр провода, но тогда увеличивается длина намотки, что снижает индуктивность, а при тесном, многослойном расположении витков наблюдается эффект «вытеснения» тока из обмотки, что увеличивает сопротивление. Эффект аналогичен вытеснению тока на высоких частотах в любых проводниках, в результате чего ток течет только в тонком скин-слое у поверхности проводника. Толщина скин-слоя уменьшается, а сопротивление провода растет пропорционально корню квадратному из частоты.

Таким образом, для получения нужных индуктивности и добротности совсем не обязательно выбирать самый толстый провод. Например, если однослойную катушку (см. рис. 23) намотать толстым проводом виток к витку или вдвое более тонким проводом, но с шагом, равным диаметру провода, индуктивность останется прежней и добротность почти не уменьшится. Добротность возрастает при увеличении вместе с диаметром провода всех размеров катушки, главным образом, ее диаметра.

Для получения максимальной добротности и индуктивности катушку выгоднее делать короткой, но большого диаметра, с отношением D/l

порядка 2,5. Индуктивность таких катушек более точно рассчитывается по эмпирической (подобранной опытным путем) формуле

где размеры берутся в сантиметрах, а индуктивность получается в микрогенри. Любопытно, что эта же формула применима для спиральной или корзиночной плоской катушки (рис. 25).

В качестве D берут средний диаметр:

D = (Dmax + Dmin)/2

а в качестве l

— ширину намотки,

l

= (Dmax — Dmin)/2.

Индуктивность многослойной катушки без сердечника (рис. 26) вычисляется по формуле

где размеры подставляются в сантиметрах, а индуктивность получается в микрогенри. При плотной рядовой намотке добротность не превосходит 30…50, «рыхлая» намотка (внавал, универсаль) дает большие значения добротности. Еще лучше «сотовая» намотка, теперь практически забытая. На частотах до 10 МГц добротность увеличивается при использовании литцендрата — провода, скрученного из многих тонких изолированных жилок. У литцендрата больше общая поверхность провода, по которой, собственно, и течет ток из-за скин-эффекта, а следовательно, меньше сопротивление на высокой частоте.

Подстроечник из магнитодиэлектрика увеличивает индуктивность вплоть до 2-3 раз, в зависимости от размеров подстроечника. Еще большее увеличение индуктивности дают замкнутые или частично замкнутые магнитопроводы, например, горшкообразные. В этом случае лучше пользоваться строгой формулой для соленоида или тора (см. выше). Добротность катушки на замкнутом магнитопроводе определяется не столько проводом, сколько потерями в материале сердечника.

В заключение главы приведем несколько полезных формул для подсчета активного сопротивления проводов. Погонное сопротивление (на метр длины) медного провода на постоянном токе и низких частотах (Ом/м) легко найти по формуле

FL = 0,0223/d2,

где d — диаметр провода, мм. Толщина скин-слоя для меди (мм) примерно равна 1/15√f

(МГц). Обратите внимание: уже на частоте 1 МГц ток проникает в провод на глубину всего 0,07 мм! В случае, когда диаметр провода больше толщины скин-слоя, сопротивление возрастает по сравнению с сопротивлением на постоянном токе. Погонное сопротивление провода на высокой частоте оценивают по формуле

R = √f/12d (мм).

К сожалению, эти формулы нельзя использовать для определения активного сопротивления катушек, поскольку из-за эффекта близости витков оно получается еще больше.

Соединения резисторов, конденсаторов и индуктивностей

Последовательное и параллельное соединения в электротехнике это два основных способа соединения элементов электрической цепи. При последовательном соединении все элементы связаны друг с другом так, что включающий их участок цепи не имеет ни одного узла. При параллельном соединении все входящие в цепь элементы объединены двумя узлами и не имеют связей с другими узлами, если это не противоречит условию.

При последовательном соединении проводников сила тока во всех проводниках одинакова. При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов. При этом величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.

При последовательном соединении резисторов R1, R2, …, Rn

общее сопротивление цепи равно сумме сопротивлений отдельных резисторов:

Rобщ = R1 + R2 + … + Rn

При параллельном соединении n

резисторов проводимость всей цепи равна сумме проводимостей всех резисторов (на основании данного ниже выражения можно определить сопротивление цепи при параллельном соединении n резисторов):

1/Rобщ = 1/R1 + 1/R2
+ … + 1/Rn
При параллельном соединении n

конденсаторов общая емкость цепи равна сумме емкостей отдельных конденсаторов:

Собщ = С1 + С2 + … + Сn

При последовательном соединении n

конденсаторов общая их емкость:

1/Собщ = 1/С1 + 1/С2 + … + 1/Сn

При последовательном соединении n

катушек индуктивности, без взаимоиндукции, общая индуктивность цепи равна сумме индуктивностей отдельных катушек:

Lобщ = L1
+L2+ … +Ln
При параллельном соединении n

катушек индуктивностей, без взаимоиндукции, общая индуктивность всей цепи определяется по формуле:

1/Lобщ = 1/L1 + 1/L2 + …
+ 1/Ln
Если магнитное поле одной катушки пересекает витки другой, т.е. катушки обладают взаимоиндукцией, то при последовательном соединении двух катушек общая индуктивность:

Lобщ
=L1+L2± 2М
,

где М

– взаимоиндукция (Гн).

При параллельном соединении двух катушек:

Lобщ
= (L1∙L2–M2) / (L1∙L2± 2М)
,

где знак плюс перед членом 2М

ставят при согласном включении катушек, а минус – при встречном;

взаимоиндукция: М = k ∙ √ (L1
∙L2)
,

где k

– коэффициент связи (
k> 1
), который зависит от взаимного расположения катушек индуктивностей
L1
и
L2
, способа намоток катушек индуктивностей и др.

Индуктивность тороидальной катушки (мкГн):

L
= 4 ∙ ∏ ∙ µ ∙F(ω2/l) ∙ 10-3
,

где ω

– число витков;

µ

– абсолютная магнитная проницаемость материала;

F

– площадь поперечного сечения магнитопровода (см2);

l

– средняя длинна магнитной линии (см).

Индуктивность однослойной цилиндрической катушки при l > 0,3D

:

L
=ω2∙D2/ (100 ∙l+ 45 ∙D)
,

где l

– длинна катушки (см);

D

– диаметр катушки (см).