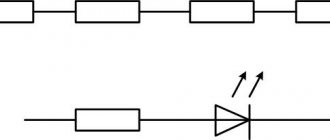
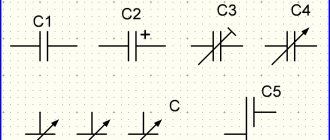Резистор представляет собой устройство, обладающее устойчивым, стабильным значением сопротивления. Это позволяет выполнять регулировку параметров на любых участках электрической цепи. Существуют различные виды соединений, в том числе и смешанное соединение резисторов. От использования того или иного способа в конкретной схеме, напрямую зависит падение напряжений и распределение токов в цепи. Вариант смешанного соединения состоит из последовательного и параллельного подключения активных сопротивлений. Поэтому в первую очередь нужно рассматривать эти два вида соединений, чтобы понять, как работают другие схемы.
Последовательное соединение
Последовательная схема подключения предполагает расположение резисторов в схеме таким образом, что конец первого элемента соединяется с началом второго, а конец второго – с началом третьего и т.д. То есть все резисторы поочередно следуют друг за другом. Сила тока при последовательном соединении будет одинаковой в каждом элементе. В виде формулы это выглядит следующим образом: Iобщ = I1 = I2, где Iобщ является общим током цепи, I1 и I2 – соответствуют токам 1-го и 2-го резистора.
В соответствии с законом Ома, напряжение источника питания будет равно сумме падений напряжения на каждом резисторе: Uобщ = U1 + U2 = I1r1 + I2r2, в которой Uобщ – напряжение источника электроэнергии или самой сети; U1 и U2 – значение падений напряжения на 1-м и 2-м резисторах; r1 и r2 – сопротивления 1-го и 2-го резисторов. Поскольку токи на любом участке цепи имеют одинаковое значение, формула приобретает вид: Uобщ = I(r1 + r2).
Таким образом, можно сделать вывод, что при последовательной схеме включения резисторов, электрический ток, протекающий через каждый из них равен общему значению тока во всей цепи. Напряжение на каждом резисторе будет разное, однако их общая сумма составит значение, равное общему напряжению всей электрической цепи. Общее сопротивление цепи также будет равно сумме сопротивлений каждого резистора, включенного в эту цепь.
Смешанное соединение пассивных элементов. Метод свертывания.
Смешанным соединением элементов называют все возможные
сочетания последовательного и параллельного соединений. В такой цепи может быть различное число узлов и ветвей. Один из примеров смешанного соединения представлен на схеме (рис. 1.3, а).
а) б)
в)
Рис.1.3 Схема смешанного соединения элементов (а) и ее эквивалентные схемы (б, в)
Для расчета такой схемы необходимо сначала определить эквивалентные сопротивления тех частей схемы, которые представляют собой только последовательное или только параллельное соединение. В предложенной схеме элементы R1
и
R2
соединены между собой последовательно, а элементы
R3
и
R4
– параллельно. Используя приведенные ранее соотношения (1.7) и (1.13), можно заменить
R1
и
R2
эквивалентным сопротивлением
R12,
а элементы
R3
и
R4
–эквивалентным сопротивлением
R34:
R12 = R1+R2 (1.18) R34 = (1.19)
В результате такой эквивалентной замены получится схема, изображенная рис.1.3 (б), в которой элементы R12 и R34 соединены между собой последовательно. Для этой схемы эквивалентное сопротивление
Rэкв=R12 + R34 (1.20) В результате такой эквивалентной замены получим схему, изображенную на рис.1.3 (в). Определим ток, протекающий в этой цепи:
(1.21) Это ток источника питания и ток в элементах R1
иR2 реальной цепи. Найдем напряжения на участке цепи с сопротивлением R12 и на участке цепи с сопротивлением R34:
U12 = I·R12
;
U34 = I ·R34
(1.22)
Токи I3 и I4 можно найти по закону Ома:
(1.23) Для проверки правильности расчета схемы смешанного соединения элементов можно воспользоваться 1-м и 2-м законами Кирхгофа, а также законом баланса мощности. Должны выполняться соотношения:
I = I3 + I4 ; Uист = U12 + U34 ; Рист=ΣРпр= Р1 + Р2 + Р3 + Р4
Здесь Р1 = ·
R1 ; Р2 =
·
R2 ; Р3 =
·
R3 ; Р4 =
·
R4 .
Подобным образом можно рассчитать и другие, более сложные схемы электрических цепей со смешанным соединением элементов.
Существуют и другие схемы эквивалентных преобразований, так как не все схемы сводятся к комбинации последовательно и параллельно соединенных элементов. Такие схемы будут рассмотрены в следующем подразделе.
Метод свертывания используется для цепей со смешанным соединением потребителей, то есть, когда есть участки с последовательным и параллельным соединением потребителей.
Параметры цепи при параллельном соединении
Параллельное соединение представляет собой включение начальных выходов двух и более резисторов в единой точке, и концов этих же элементов в другой общей точке. Таким образом, фактически происходит соединение каждого резистора непосредственно с источником электроэнергии.
В результате, напряжение каждого резистора будет одинаковым с общим напряжением цепи: Uобщ = U1 = U2. В свою очередь, значение токов будет разным на каждом резисторе, их распределение становится прямо пропорциональным сопротивлению этих резисторов. То есть, при увеличении сопротивления, сила тока уменьшается, а общий ток становится равен сумме токов, проходящих через каждый элемент. Формула для данного положения выглядит следующим образом: Iобщ= I1 + I2.
Для расчетов общего сопротивления используется формула: . Она используется при наличии в цепи только двух сопротивлений. В тех случаях, когда сопротивлений в цепи подключено три и более, применяется другая формула:
Таким образом, значение общего сопротивления электрической цепи будет меньше, чем самое минимальное сопротивление одного из резисторов, подключенных параллельно в эту цепь. На каждый элемент поступает напряжение, одинаковое с напряжением источника электроэнергии. Распределение тока будет прямо пропорциональным сопротивлению резисторов. Значение общего сопротивления резисторов, соединенных параллельно, не должно превышать минимального сопротивления какого-либо элемента.
Читать также: Какие величины определяют потенциальную энергию растянутой пружины
Смешанное соединение и сложные электрические цепи
Частым явлением в электрических цепях считается соединение смешанного типа (то есть комбинирование параллельного и последовательного соединений).
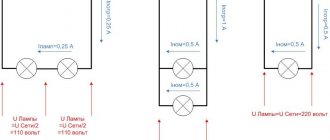
Если, например, взять 3 прибора, то возможными будут два варианта смешанного соединения. В первом случае мы наблюдаем соединение двух приборов параллельным образом при последовательном подключении к ним третьего.
При условии большего количества приборов, схемы смешанного соединения будут более сложными. Иногда встречаются также усложненные цепи, содержащие несколько ЭДС-источников.
Для расчета сложных цепей применяются различные методики. Наиболее распространенной считается методика, основанная на применении второго закона Кирхгофа. В наиболее общем формате закон сформулирован таким образом: в каком-либо замкнутом контуре алгебраическая сумма ЭДС будет равнозначной такого же типа сумме падений напряжений.
Алгебраическая сумма берется по той причине, что ЭДС, действующие встречным образом в отношении друг друга, или созданные противоположно направленными токами напряжения будут иметь разные знаки.
Готовые работы на аналогичную тему
При расчетах сложной цепи в большинстве примеров бывают известными сопротивления отдельных участков цепи и ЭДС, включенных источников. Для нахождения токов следует (на основе второго закона Кирхгофа) составить уравнения (для замкнутых контуров), в которых токи будут считаться неизвестными величинами.
К таким уравнениям также добавляются уравнения для точек разветвления, составленные по принципу первого закона Кирхгофа. При решении такой системы уравнений определяются токи. В случае с более сложными цепями, подобный метод будет достаточно громоздким, что обусловлено наличием большого числа неизвестных.
Последовательное и параллельное соединение: формулы как найти силу тока, общее сопротивление, напряжение
При разработке электрических цепей применяется последовательное и параллельное соединение проводников. Умение анализировать (как количественно, так и качественно) и рассчитывать такие схемы является базовым принципом знаний электротехники.
Мнение эксперта
It-Technology, Cпециалист по электроэнергетике и электронике
Задавайте вопросы «Специалисту по модернизации систем энергогенерации»
Общее сопротивление цепи — определение, правила, задачи Параллельное подключение это такое подсоединение источников, в котором входы всех устройств находятся в одних местах, а выходы в других. Спрашивайте, я на связи!
Схема смешанного соединения резисторов
Схема смешанного соединения обладает свойствами схем последовательного и параллельного соединения резисторов. В этом случае элементы частично подключаются последовательно, а другая часть соединяется параллельно. На представленной схеме резисторы R1 и R2 включены последовательно, а резистор R3 соединен параллельно с ними. В свою очередь резистор R4 включается последовательно с предыдущей группой резисторов R1, R2 и R3.
Расчет сопротивления для такой цепи сопряжен с определенными трудностями. Для того чтобы правильно выполнить расчеты используется метод преобразования. Он заключается в последовательном преобразовании сложной цепи в простейшую цепь за несколько этапов.
Если для примера вновь использовать представленную схему, то в самом начале определяется сопротивление R12 резисторов R1 и R2, включенных последовательно: R12 = R1 + R2. Далее, нужно определить сопротивление резисторов R123, включенных параллельно, по следующей формуле: R123=R12R3/(R12+R3) = (R1+R2)R3/(R1+R2+R3). На последнем этапе выполняется расчет эквивалентного сопротивления всей цепи, путем суммирования полученных данных R123 и сопротивления R4, включенного последовательно с ним: Rэк = R123 + R4 = (R1 + R2) R3 / (R1 + R2 + R3) + R4.
В заключение следует отметить, что смешанное соединение резисторов обладает положительными и отрицательными качествами последовательного и параллельного соединения. Это свойство успешно используется на практике в электрических схемах.
топологические понятия, элементы, схема замещения
2.Законы Ома и Кирхгофа для цепей постоянного тока
3.Последовательное, параллельное и смешанное соединение потребителей
Последовательное, параллельное и смешанное соединения резисторов. Значительное число приемников, включенных в электрическую цепь (электрические лампы, электронагревательные приборы и др.), можно рассматривать как некоторые элементы, имеющие определенное сопротивление. Это обстоятельство дает нам возможность при составлении и изучении электрических схем заменять конкретные приемники резисторами с определенными сопротивлениями. Различают следующие способы соединения резисторов (приемников электрической энергии): последовательное, параллельное и смешанное.
Последовательное соединение резисторов. При последовательном соединении нескольких резисторов конец первого резистора соединяют с началом второго, конец второго — с началом третьего и т. д. При таком соединении по всем элементам последовательной цепи проходит один и тот же ток I. Напряжение U на зажимах источника равно сумме напряжений на каждом из последовательно включенных резисторов.
Параллельное соединение резисторов. При параллельном соединении нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви.
При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:
I1=U/R1; I2=U/R2; I3=U/R3.
Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I1+I2+I3,
Смешанное соединение резисторов. Смешанным соединением называется такое соединение, при котором часть резисторов включается последовательно, а часть — параллельно. Например, в схеме рис. 27, а имеются два последовательно включенных резистора сопротивлениями R1 и R2, параллельно им включен резистор сопротивлением Rз, а резистор сопротивлением R4 включен последовательно с группой резисторов сопротивлениями R1, R2 и R3.
4.Расчёт цепи постоянного тока методами контурных токов и узловых потенциалов
Метод контурных токов. В основе лежит 2-й закон Кирхгофа. Суть метода в ведении фиктивных контурных токов и их расчёт.
1.Определение числа уравнений: у=в-ви.т-(n-1).
В-число ветвей, ви.т-с источником тока,n-число узлов.
2.Составляем уравнения для неизвестных контурных токов в общем виде.
3.Определяем неизвестные коэффициенты левой и правой части (Е и R).
4.Подставив коэффициенты, решаем уравнения, находим токи контуров.
5.Определяем через контурные токи токи в ветвях.
Метод узловых потенциалов. В основе лежит 1-й закон Кирхгофа. Определяем потенциалы узлов цепи с последующим определением токов в ветвях, используя закон Ома для участков цепи.
1.Подготовка схемы. Обозначим узлы. Потенциал одного из них принимаем за 0.
2.Составляем уравнения потенциалов в общем виде:
Фи1*g11 + фи2*g12 = I11 – для первого узла
Фи1g21 + фи*g22 = I22 – для второго узла
3.Определяем неизвестные проводимости gmn –сумма проводимостей ветвей, подходящих к узлу n.
4.Подставив, решаем уравнения, находим фи1 и фи2.
5.Произвольно выбираем направления токов и, используя закон Ома для участка цепи определяем эти токи: In = (фиX-фиY+En)/Rn.
ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ РЕЗИСТОРОВ
Это такое соединение, при котором все элементы идут один за одним без разветвлений.
Свойства последовательного соединения
1. Ток во всех резисторах одинаков- I 1 = I 2 = I 3 ;
2. Общее напряжение цепи равно сумме напряжений на всех резисторах- U=U 1 + U 2 + U 3 ;
3.Сопротивление по отношению к входным зажимам называется входным сопротивлением и равно сумме сопротивлений участков – R вх = R 1 + R 2 + R 3 ;
4. Чем больше сопротивление участка, тем больше на нём падает напряжение-.
ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ РЕЗИСТОРОВ
Это такое соединение, при котором все начала элементов соединяются в одну точку, а все концы в другую и к этим точкам подводится напряжение.
Свойства параллельного соединения резистора:
1. Общее напряжение цепи равно напряжению на каждом участке-
U = U 1 = U 2 = U 3
2. Общий ток цепи равен сумме токов на всех участках- I = I 1 + I 2 + I 3
3. Чтобы найти входное сопротивление, рассчитывают вначале величину обратную входному сопротивлению
– проводимость ( G )
Общая проводимость цепи равна сумме проводимостей на каждом участке.
G = G 1 + G 2 + G 3
4.Чем больше сопротивление участка, тем меньше ток, протекающий на нем.
При параллельном соединении двух резисторов формулу входного сопротивления можно преобразовать
1.
2. Если известен общий ток, то можно найти ток ветви, умножив общий ток на сопротивление противоположной ветви и разделить на сумму сопротивлений ; .
Задание
Варианты ответов
1.Являются ли при последовательном соединении резисторов напряжения участков пропорционально сопротивлениям этих участков.
2.Являются ли при параллельном соединении резисторов токи ветвей пропорциональны сопротивлениям этих ветвей.
3.Укажите по какому из приведенных математических выражений нельзя рассчитать входное сопротивление двух параллельно соединенных резисторов.
а) ; б);
в) ; г)