Колебательный LC контур: определение, принцип действия, расчет

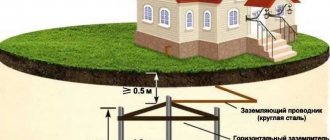
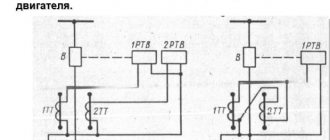
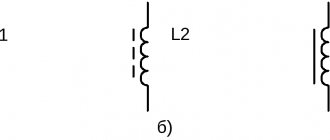
Сегодня нас интересует простейший колебательный контур, его принцип работы и применение.

За полезной информацией по другим темам переходите на наш телеграм-канал.

Колебания – процесс, повторяющийся во времени, характеризуется изменением параметров системы около точки равновесия.

Первое, что приходит на ум — это механические колебания математического или пружинного маятников. Но ведь колебания бывают и электромагнитными.

По определению колебательный контур (или LC-контур) – это электрическая цепь, в которой происходят свободные электромагнитные колебания.

Такой контур представляет собой электрическую цепь, состоящую из катушки индуктивностью L и конденсатора емкостью C. Соединены эти два элемента могут быть лишь двумя способами — последовательно и параллельно. Покажем на рисунке ниже изображение и схему простейшего колебательного контура.

Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.

Принцип действия колебательного контура

Давайте рассмотрим пример, когда сначала мы заряжаем конденсатор и замыкаем цепь. После этого в цепи начинает течь синусоидальный электрический ток. Конденсатор разряжается через катушку. В катушке при протекании через нее тока возникает ЭДС самоиндукции, направленная в сторону, противоположную току конденсатора.

Разрядившись окончательно, конденсатор благодаря энергии ЭДС катушки, которая в этот момент будет максимальна, начнет заряжаться вновь, но только в обратной полярности.

Колебания, которые происходят в контуре – свободные затухающие колебания. То есть без дополнительной подачи энергии колебания в любом реальном колебательном контуре рано или поздно прекратятся, как и любые колебания в природе.

Это обусловлено тем, что контур состоит из реальных материалов (конденсатор, катушка, провода), обладающих таким свойством, как электрическое сопротивление, и потери энергии в реальном колебательном контуре неизбежны. В противном случае это нехитрое устройство могло бы стать вечным двигателем, существование которого, как известно, невозможно.

Еще одна важная характеристика LC-контура – добротность Q. Добротность определяет амплитуду резонанса и показывает, во сколько раз запасы энергии в контуре превышают потери энергии за один период колебаний. Чем выше добротность системы, тем медленнее будут затухать колебания.

Резонанс токов в параллельном колебательном контуре

Рассмотрим случай параллельного соединения колебательного контура с источником тока (рис. 1) и посмотрим, каково будет сопротивление контура для токов различных частот в этом случае. Если частота тока невелика (ниже резонансной), то почти весь ток пойдет по наиболее легкому для него пути — через индуктивную ветвь; сопротивление контура при низких частотах будет небольшим по величине и индуктивным по своему характеру.

Для токов высоких частот (выше резонансной) более легким путем будет путь через емкостную ветвь, и, следовательно, сопротивление контура будет также небольшим по величине, но емкостным по характеру.

При резонансной частоте, когда емкостное сопротивление равно индуктивному, путь для тока будет одинаково трудным через обе ветви. Мы знаем, что при параллельном соединении двух равных сопротивлений общее сопротивление равняется половине любого из них. Поэтому, казалось бы, что сопротивление контура при резонансе должно равняться половине одного из реактивных сопротивлений. Однако, не следует забывать, что мы имеет дело, с сопротивлениями, хотя и одинаковыми по величине, но имеющими принципиально различный характер. Это различие проявляется в том, что токи в индуктивной и емкостной ветвях контура сдвинуты по фазе друг относительно друга на 180°. Отсюда непосредственно следует, что в неразветвленной части цепи всегда протекает не суммарный, а разностный ток (рис. 1).

Рисунок 1. Токи при параллельном резонансе. В неразвлетвленной части цепи протекает не скммарный, а разностный ток.

Поэтому при резонансе, когда токи в емкостной и индуктивной ветвях равны между собой, ток в неразветвленной части цепи будет равен нулю, какое бы напряжение мы ни прилагали к контуру. При резонансе между точками АВ цепь будет казаться разорванной, т. е. сопротивление ее между этими точками будет бесконечно велико, а отнюдь не будет равным половине одного из реактивных сопротивлений. Практически бесконечно большого сопротивления контура при резонансе не бывает, так как из-за наличия активного сопротивления в контуре (сопротивление провода катушки) сдвиг фаз токов никогда не может быть равным точно 180°.

Однако активное сопротивление катушки обычно бывает много меньше ее индуктивного сопротивления, и поэтому сопротивление колебательного контура при резонансе может достигать очень больших величин.

Сопротивление колебательного контура при параллельном резонансе равно:

где L выражено в гн, С—в ф, RL—в ом.

Полное сопротивление колебательного контура при резонансе является чисто активным в силу того обстоятельства, что индуктивное и емкостное сопротивления взаимно компенсируются.

Кривые изменения полного сопротивления колебательного контура между точками АВ при изменении частоты тока приведены на рис. 2,б.

Рисунок 2. Резонанс токов. а) — схема и обозначения; б) — график полного сопротивления.

При параллельном резонансе токи ,в ветвях контура достигают наибольшей величины; поэтому параллельный резонанс называется резонансом токов.

Явление резонанса имеет огромнейшее значение в радиотехнике. На земном шаре имеется большое количество передающих радиостанций. Передачи всех этих радиостанций распространяются в эфипе и все одновременно принимаются приемной антенной. Нетрудно представить себе, каким получилось бы нагромождение друг на друга передач, если бы мы не могли выделить из этого хаоса только одну нужную нам. Вот тут-то на помощь приходит явление резонанса. Передающие радиостанции излучают в пространство электромагнитную энергию на различных частотах, мы же, настраивая контуры нашего приемника в резонанс с той или иной частотой, тем самым выбираем нужную нам передачу.

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Резонанс LC-контура

Электромагнитные колебания в LC-контуре происходят с определенной частотой, которая называется резонансной Подробнее про резонанс– в нашей отдельной статье. Частоту колебаний можно менять, варьируя такие параметры контура, как емкость конденсатора C, индуктивность катушки L, сопротивление резистора R (для LCR-контура).

Как рассчитать резонансную частоту колебательного контура? Очень просто! Приведем окончательную формулу:

Параллельный контур

На рис. 101, а представлен колебательный контур с параллельно включенными элементами L и С по отношению к приложенной э. д. с. (параллельный контур

). Если частота ее совпадает с частотой свободных колебаний контура, то возникает резонанс токов.

В этом случае, как видно из векторной диаграммы (рис. 101,б), токи в обеих ветвях контура равны между собой, так как равны друг другу полные сопротивления индуктивной (Z1) и емкостной (Z2) ветвей. Но при этом создаются сдвиги по фазе между токами и относительно приложенной э. д. с.

Рис. 101. Вынужденные колебания в контуре с параллельно включенными элементами: а — схема включения; б — векторная диаграмма (резонанс токов); в — зависимость сопротивления контура и тока в питающем проводе от частоты.

Из векторной диаграммы также следует, что ток I в неразветвленной части цепи при резонансе минимален, а стало быть, сопротивление максимально и активно (вектор тока / и вектор э. д. с. Е совпадают по фазе). Сопротивление, эквивалентное контуру при резонансе,

где r1, r2 — активные сопротивления соответствующих ветвей контура; X — реактивное сопротивление любой из них; R — полное активное сопротивление потерь.

Если Х1 и Х2 заменить их значениями, то можно получить формулу, устанавливающую связь между сопротивлением контура при резонансе и элементами контура:

(155)

Следует отметить, что равенство реактивных сопротивлений обеих ветвей контура является достаточным условием для определения резонансной частоты ƒ0=1/2π√LC лишь при равенстве активных потерь в ветвях контура. Если активные потери в ветвях контура неодинаковы, то резонансная частота, определенная по приведенной выше формуле, должна быть скорректирована, т. е. контур следует подстроить.

Выразив индуктивность катушки в микрогенри, частоту в мегагерцах, а емкость контура в пикофарадах, получаем формулу, устанавливающую связь между этими величинами в следующем виде:

Определение добротности, приведенное ранее для последовательного контура, здесь не подходит, так как напряжение на элементах контура, независимо от его настройки, равно Uк(см. рис. 101, а). Физический смысл добротности для параллельного колебательного контура

можно получить, приравняв следующие выражения, определяющие напряжение на контуре:

Uк = IRэ = Iкρ

откуда

(156)

Добротность Q показывает, во сколько раз ток в контуре при резонансе больше тока в неразветвленной цепи.

На частотах ниже резонансной сопротивление индуктивной ветви меньше сопротивления емкостной ветви контура и, следовательно, ток в индуктивной ветви становится больше тока в емкостной ветви. Поэтому контур на частотах ниже резонансной, по отношению к источнику э. д. с, представляет собой индуктивную нагрузку.

На частотах выше резонансной картина становится противоположной и параллельный колебательный контур ведет себя как емкостная нагрузка.

Параллельный колебательный контур

обычно включают в анодную цепь лампы. При анализе такой схемы лампу заменяют эквивалентным генератором переменного тока с э. д. с, равной μUс (где Uс — напряжение входного сигнала на управляющей сетке лампы), с внутренним сопротивлением Ri (рис. 102, а). В зависимости от соотношения величин сопротивлений Ri и Rэ при резонансе, можно судить о настройке контура в резонанс либо по поведению тока в неразветвленной цепи, либо по поведению напряжения на зажимах контура.

Рис. 102. Настройка параллельного контура: а — эквивалентная схема включения контура в анодную цепь электронной лампы; б — график I и Uк= φ (ƒ) при Ri<э; в — график I и Uк = φ (ƒ) при Ri<э; г — график I и Uк = φ (ƒ) при Ri<э.

Ток в неразветвленной цепи равен

Напряжение на зажимах контура

Uк= I Rэ

Если Ri<< Rэ (что имеет место при включении контура в анодную цепь), то при настройке контура, в момент резонанса, ток в питающем проводе будет минимален, а напряжение на зажимах контура будет меняться незначительно. Так как по мере приближения к резонансу сопротивление контура растет, а ток в неразветвленной цепи падает, то произведение этих величин, представляющее напряжение на контуре, остается почти неизменным. Таким образом, в рассматриваемом случае судить о настройке контура в резонанс можно только по минимуму тока в питающем проводе (рис. 102, б).

Если Ri >> Rэ то, рассуждая подобным же образом, легко прийти к выводу, что при настройке контура ток в питающем проводе остается почти неизменным. Следовательно, о настройке контура в резонанс можно судить лишь по поведению напряжения на зажимах контура (рис. 102, в).

Особый интерес представляет третий случай, когда Ri и Rэ соизмеримы, т. е. Ri≈ Rэ. В этом случае о настройке контура в резонанс можно судить как по поведению напряжения па зажимах контура, так и по поведению тока в неразветвленной цепи (рис. 102, г).

Полоса пропускания параллельного контура

по току может быть определена по формуле (153) для полосы пропускания последовательного контура лишь при Ri = 0. К этому же выводу можно прийти при определении полосы пропускания по напряжению при Ri = ∞:

2∆ƒ1 = ƒ0/Q при Ri = 0; 2∆ƒU = ƒ0/Q при Ri→∞.

При Ri = Rэ полосы пропускания по току и по напряжению могут быть определены по формулам

Полоса пропускания по напряжению получается шире полосы пропускания по току. Это объясняется тем, что внутреннее сопротивление генератора шунтирует контур, т. е. как бы увеличивает потери в нем. Поэтому иногда, для расширения полосы пропускания контура, его специально шунтируют сопротивлением. Дополнительные потери ∆r, вносимые в контур, определяются по формуле

(157)

где X — реактивное сопротивление ветви контура; Rш — шунтирующее сопротивление. Добротность контура при учете влияния сопротивления шунта определяется формулой

Известно, что наибольший ток в электрической цепи имеет место при равенстве внутреннего сопротивления источника и сопротивления нагрузки, поэтому при рассмотрении эквивалентной схемы, приведенной на рис. 102, а, можно сделать также вывод, что максимальный ток в цепи, а следовательно, и максимальное напряжение на зажимах контура и максимальная мощность в контуре, будут выделяться при Ri = Rэ. Значит, колебательный контур, включенный в анодную цепь лампы, должен быть не только настроен на частоту сигнала, но и представлять собой сопротивление, обеспечивающее наиболее целесообразный режим работы электронной лампы.

В связи с этим, в отличие от контура, представленного на рис. 102, a, называемого контуром первого вида, применяются колебательные контуры, в которых индуктивности или емкости распределены между ветвями контура. Они называются соответственно контурами второго и третьего видов (рис. 103, а, б). Настройка контура не изменится при любом перераспределении элементов L и С между ветвями контура при условии, что полные значения этих величин останутся неизменными.

Так, например, если емкость конденсатора контура составляла 100 пф, то настройка контура не изменится при замене этой емкости двумя последовательно включенными в контур конденсаторами емкостью по 200 пф каждый.

Рис. 103. Колебательные контуры второго (а) и третьего (б) видов.

Иначе обстоит дело с сопротивлениями контуров второго и третьего видов при резонансе.

Рассмотрим контур второго вида, в котором индуктивность L распределена между ветвями контура. Сопротивление параллельного контура при резонансе, согласно определению, равно X21,2/R. В нашем случае Х1 = ω0L1, а не ω0L = ω0 (L1 + L2), как это было в контуре первого вида. Поэтому сопротивление контура второго вида при резонансе

Умножим числитель и знаменатель на L, тогда

(158)

Коэффициент включения или коэффициент, учитывающий распределение индуктивности L между ветвями контура, р = L1/L<1, следовательно, сопротивление контура второго вида при резонансе меньше сопротивления контура первого вида.

К подобному же выводу можно прийти при рассмотрении контура третьего вида, сопротивление которого при резонансе

Rэ III=q2Rэ (159)

где q=С/С1<1 (так как С=C1C2/C1+C2)

Таким образом, перераспределяя индуктивность или емкость между ветвями контура, можно осуществлять переход от контура одного вида к контуру другого вида. Такой переход позволяет сохранять настройку неизменной, изменять сопротивление контура при резонансе и тем самым обеспечить его согласование (равенство) с внутренним сопротивлением электронной лампы.

Последовательный контур

Для последовательного колебательного контура характерно наличие последовательного соединения емкости с индуктивностью. При этом эти два элемента не влияют на потери энергии в цепи и являются идеальными элементами.

Потери в данной схеме вызваны только наличием активной нагрузки. Ниже представлен график амплитудно-частотной характеристики такой схемы.

Для такой цепи сопротивление катушки и конденсатора являются паразитными, приводят к появлению резонанса. Данный резонанс выравнивает или обнуляет сопротивления, оставляя только влияние активной нагрузки R от резистора. При этом добротность такой электроцепи определяется, как разницу напряжений на источнике тока и выходах катушки/конденсатора. В этом случае Q определяют с помощью следующего выражения:

В данной формуле:

С — емкость конденсатора.
L — индуктивность катушки.
R — потери сопротивления.

Для примера попробуем решить следующую задачу. В цепи имеется катушка индуктивности L=100 мГн с сопротивлением R=100 Ом, которая соединена последовательно с конденсатором емкостью C=0.07 мкФ. Найдите резонансную частоту ω0, характеристическое сопротивление и добротность колебательного контура.

Вычисляем резонансную частоту контура:

Определяем характеристическое сопротивление:

Конечный шаг — вычисление добротности контура: