Формулы расчета последовательного колебательного контура

Параллельный колебательный контур

Идеальный колебательный контур

На схеме идеальный колебательный контур выглядит вот так:

где

L — индуктивность, Генри

С — емкость, Фарад

Реальный колебательный контур

В реальности у нас катушка обладает приличным сопротивлением потерь, так как намотана из провода, да и конденсатор тоже имеет некоторое сопротивление потерь. Потери в емкости очень малы и ими обычно пренебрегают. Поэтому оставим только одно сопротивление потерь катушки R. Тогда схема реального колебательного контура примет вот такой вид:

где

R — это сопротивление потерь контура, Ом

L — индуктивность, Генри

С — емкость, Фарад

Принцип работы параллельного колебательного контура

Давайте подцепим к генератору частоты реальный параллельный колебательный контур

Что будет, если мы подадим на контур ток с частотой в ноль Герц, то есть постоянный ток? Он спокойно побежит через катушку и будет ограничиваться лишь сопротивлением потерь R самой катушки. Через конденсатор ток не побежит, потому что конденсатор не пропускает постоянный ток. Об это я писал еще в статье конденсатор в цепи постоянного и переменного тока.

Давайте тогда будем добавлять частоту. Итак, с увеличением частоты у нас конденсатор и катушка начнут оказывать реактивное сопротивление электрическому току.

Реактивное сопротивление катушки выражается по формуле

а конденсатора по формуле

Более подробно про это можно прочитать в этой статье.

Если плавно увеличивать частоту, то можно понять из формул, что в самом начале при плавном увеличении частоты конденсатор будет оказывать бОльшее сопротивление, чем катушка индуктивности. На какой-то частоте реактивные сопротивления катушки XL и конденсатора XC уравняются. Если далее увеличивать частоту, то уже катушка уже будет оказывать большее сопротивление, чем конденсатор.

Виды и особенности

Схемы колебательных контуров бывают двух видов: последовательными и параллельными. Они отличаются типом соединения элементов емкости и индуктивности. В первом случае они соединены последовательно, а во втором — параллельно. Для работы необходима постоянная электрическая энергия, в противном случае происходит ее затухание, поскольку часть уходит на генерацию электромагнитного поля и нагрев провода обмотки катушки индуктивности. Контур также может быть открытым и закрытым. Открытый выпускается без специальной защитной крышки.

При решении задач по физике можно встретить интересное понятие — идеальный колебательный контур. Если в задании встречается такой термин, то это говорит о том, что энергия остается в системе, а не уходит на описанные выше процессы.

Устройство постоянно генерирует электромагнитные колебания, то есть является подобием вечного двигателя, однако такого не может быть вообще. На практике при расчете параметров учитываются затухания — постепенные уменьшения амплитуды электромагнитной волны.

Последовательное соединение

Последовательный контур — простейшая резонансно-колебательная система. Он состоит из двух элементов, подсоединенных последовательно. Через них при подключении переменного напряжения будет протекать ток переменной составляющей. Его величина определяется по закону Ома: i = U / Zlc. В этой формуле Zlc является суммой реактивных сопротивлений катушки индуктивности (Xl) и конденсатора (Xc).

Величины определяются по формулам Xl = wL и Xc = 1 / (wC). Параметр w — угловая частота, которую можно найти по такому соотношению через частоту переменного тока и число Pi: w = 2 * Pi * f. Из соотношений можно сделать вывод, что реактивное сопротивление на индуктивности растет с увеличением f, а для емкости — уменьшается. В первом случае тип зависимости называется прямо пропорциональным, а во втором — обратно пропорциональным.

При определенном значении частоты сопротивления двух элементов равны по модулю друг другу. Следовательно, это явление называется резонансом колебательной системы. Частоту w при таком условии называют собственной резонансной частотой контура. Рассчитать ее довольно просто, поскольку следует приравнять две формулы для получения уравнения: wL = 1 / (wC). Далее нужно выразить значение f: f = [(1 / (L * C))^(½)] / 2Pi. Последнее соотношение называется формулой Томсона.

Когда контур подключается к цепи генератора (источника) переменного напряжения с активным сопротивлением R, полный импеданс цепи (Z) определяется с помощью соотношения Z = [R2 + Zlc2]^(½). Если происходит резонанс, то Z = R, а реактивная составляющая исчезает.

У контура существуют еще две важные характеристики: добротность (Q) и характеристическое сопротивление (р). Последней называется величина сопротивления реактивного типа при резонансе. Вычисляется она по формуле р = (L * C)^(½) и показывает количество энергии катушки и конденсатора, которое было запасено. Для емкости значение определяется по соотношению Wс = (C * U2) / 2, а для индуктивности — Wl = (L * I2) / 2.

Отношение величины энергии, которая была запасена конденсатором и катушкой, к показателю потерь называется добротностью колебательного контура (Q). Параметр определяет амплитуду и ширину АЧХ резонанса и показывает превышение энергии запаса над потерями за одно колебание. При этом учитывается реактивная нагрузка R. Характеристика определяется по формуле Q = (1 / R) * [(L / C)^(½)].

В некоторых случаях описывать добротность можно другим тождеством: Q = p / R. Современные устройства выполняются на дискретных катушках, а их Q колеблется от нескольких единиц до сотен. Системы, построенные на принципе пьезоэлектронных устройств (кварцевые резонаторы), имеют высокий показатель Q. Его значение может достигать 1 тыс. и больше. Затухание контура (d) — характеристика, которая является обратной добротности. Она определяется по такому соотношению: d = 1 / Q.

Параллельный контур

Контур параллельного типа состоит также из конденсатора и катушки. Отличие заключается в том, что эти два элемента соединены параллельно между собой. Этот тип устройства применяется чаще, чем последовательный контур. Чтобы найти общее сопротивление индуктивного характера, нельзя просто сложить значения Xl и Xc. Складываются только проводимости двух элементов.

Из курса физики известно, что проводимость — величина, обратная сопротивлению, то есть Xc = 1 / Gc и Xl = 1 / Gl. Следовательно, формулы для параллельного соединения имеют такой вид:

1. Gl = 1 / wL.
2. Gc = wC.
3. Q = R * [(С / L)^(½)].

Для примера необходимо рассмотреть электрическую цепь, состоящую из генератора переменного тока и параллельного контура. В какой-то момент времени их частоты будут совпадать. Кроме того, проводимости двух элементов равны по модулю между собой. В результате этого происходит явление резонанса токов.

В цепи будет только активное сопротивление Rэкв, которое называют в радиотехнике эквивалентным. Оно вычисляется по формуле Rэкв = Q * p. Если частота не соответствует резонансной, то в устройстве происходят другие процессы: на низких наблюдается уменьшение индуктивного сопротивления, а на высоких — емкостного.

Во время работы контура за период колебаний два раза происходит обмен энергией между катушкой и конденсатором. В радиоэлементе протекает ток, по силе превосходящий внешний в Q раз.

Резонанс параллельного колебательного контура

Очень интересное свойство параллельного колебательного контура заключается в том, что при ХL = ХС у нас колебательный контур войдет в резонанс. При резонансе колебательный контур начнет оказывать большее сопротивление переменному электрическому току. Еще часто это сопротивление называют резонансным сопротивлением контура и оно выражается формулой:

где

Rрез — это сопротивление контура на резонансной частоте

L — собственно сама индуктивность катушки

C — собственно сама емкость конденсатора

R — сопротивление потерь катушки

Расстройка устройства

Расстройка — это настройка контура на частоту, отличную от резонансной. Последняя наступает в том случае, когда характеристики частот радиодетали и генератора совпадают. В некоторых устройствах этого необходимо избегать. Чтобы получить резонанс, нужно воспользоваться одним из трех методов изменения характеристик:

• частоты генератора;
• индуктивности;
• емкости.

Два последних метода можно делать одновременно для достижения лучшего эффекта. Расстройки классифицируются на три вида: абсолютную, обобщенную и относительную. Первой называется разность между частотами контура и резонанса. Обобщенная вычисляется при помощи отношения реактивного сопротивления к активному. Относительная выражается в виде отношения абсолютной расстройки к резонансной частоте.

Кроме того, расстройка бывает положительной и отрицательной. В первом случае необходимо, чтобы частота генератора была больше частоты контура. Для отрицательной должно соблюдаться другое условие: частота генератора меньше, чем у контура.

В некоторых случаях необходимо убрать резонансную частоту. Выполняется такая операция при помощи изменения необходимых характеристик электроцепи «контур — генератор». Очень часто в контуре применяются конденсаторы с переменной емкостью, позволяющие настраивать его. Настройка конденсатора происходит благодаря изменению расстояния между его обкладками. Этот принцип очень удобен, поскольку для изменения индуктивности катушки необходим сердечник, который будет выкручиваться.

Однако существуют радиоэлементы и такого типа. В них емкость является постоянной величиной, а индуктивность изменяется с помощью сердечника. Конструктивная особенность последнего представляет обыкновенный ферритовый болт, который вкручивается в пластиковый корпус. На последний наматывается провод.

Как найти резонанс параллельного колебательного контура на практике

Ладно, ближе к делу. Берем паяльник в руки и спаиваем катушку и конденсатор параллельно. Катушка на 22 мкГн, а конденсатор на 1000пФ.

Итак, реальная схема этого контура будет вот такая:

Для того, чтобы все показать наглядно и понятно, давайте добавим к контуру последовательно резистор на 1 КОм и соберем вот такую схему:

На генераторе мы будет менять частоту, а с клемм X1 и X2 мы будем снимать напряжение и смотреть его на осциллографе.

Нетрудно догадаться, что у нас сопротивление параллельного колебательного контура будет зависеть от частоты генератора, так как в этом колебательном контуре мы видим два радиоэлемента, чьи реактивные сопротивления напрямую зависит от частоты, поэтому заменим колебательный контур эквивалентным сопротивлением контура Rкон.

Упрощенная схема будет выглядеть вот так:

Интересно, на что похожа эта схема? Не на делитель ли напряжения? Именно! Итак, вспоминаем правило делителя напряжения: на меньшем сопротивлении падает меньшее напряжение, на бОльшем сопротивлении падает бОльшее напряжение. Какой вывод можно сделать применительно к нашему колебательному контуру? Да все просто: на резонансной частоте сопротивление Rкон будет максимальным, вследствие чего у нас на этом сопротивлении «упадет» бОльшее напряжение.

У нас есть калькулятор резисторов по цветам. Самый крутой подборник.

Начинаем наш опыт. Поднимаем частоту на генераторе, начиная с самых маленьких частот.

200 Герц.

Как вы видите, на колебательном контуре «падает» малое напряжение, значит, по правилу делителя напряжения, можно сказать, что сейчас у контура малое сопротивление Rкон

Добавляем частоту. 11,4 Килогерца

Как вы видите, напряжение на контуре поднялось. Это значит, что сопротивление колебательного контура увеличилось.

Добавляем еще частоту. 50 Килогерц

Заметьте, напряжение на контуре повысилось еще больше. Значит его сопротивление еще больше увеличилось.

723 Килогерца

Обратите внимание на цену деления одного квадратика по вертикали, по сравнению с прошлым опытом. Там было 20мВ на один квадратик, а сейчас уже 500 мВ на один квадратик. Напряжение выросло, так как сопротивление колебательного контура стало еще больше.

И вот я поймал такую частоту, на которой получилось максимальное напряжение на колебательном контуре. Обратите внимание на цену деления по вертикали. Она равняется двум Вольтам.

Дальнейшее увеличение частоты приводит к тому, что напряжение начинает падать:

Снова добавляем частоту и видим, что напряжение стало еще меньше:

Радиолюбитель

Практический расчет последовательного или параллельного LC контура.

Доброго дня уважаемые радиолюбители! Сегодня мы с вами рассмотрим порядок расчета LC контура.

Некоторые из вас могут спросить, а на черта нам это нужно? Ну, во-первых, лишние знания никогда не помешают, а во-вторых, бывают в жизни моменты, когда вам знание этих расчетов может понадобиться. К примеру, очень многие начинающие радиолюбители (естественно, в основном молодые), увлекаются сборкой так называемых “жучков” – устройств позволяющих на расстоянии прослушивать что-нибудь. Конечно я уверен, что это делается без всяких нехороших (даже грязных) мыслей подслушать кого-нибудь, а в благих целях. Например устанавливают “жучок” в комнате с малышом, а на радиовещательный приемник прослушивают не проснулся ли он. Все схемы “радиожучков” работают на определенной частоте, но что делать, когда эта частота вас не устраивает. Вот тут вам придет на помощь знание нижеприведенной статьи.

LC колебательные контура применяются практически в любой аппаратуре, работающей на радиочастотах. Как известно из курса физики, колебательный контур состоит из катушки индуктивности и конденсатора (емкости), которые могут быть включены параллельно (параллельный контур) или последовательно (последовательный контур), как на рис.1:

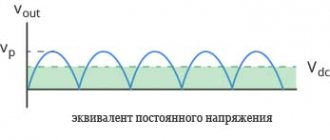
Реактивные сопротивления индуктивности и емкости, как известно, зависят от частоты переменного тока. При увеличении частоты реактивное сопротивление индуктивности растет, а емкости – падает. При уменьшении частоты, наоборот, индуктивное сопротивление падает, а емкостное – растет. Таким образом, для каждого контура есть некоторая частота резонанса, на которой индуктивное и емкостное сопротивления оказываются равными. В момент резонанса резко увеличивается амплитуда переменного напряжения на параллельном контуре или резко увеличивается амплитуда тока на последовательном контуре. На рис.2 показан график зависимости напряжения на параллельном контуре или тока на последовательном контуре от частоты:

На частоте резонанса эти величины имеют максимальное значение. А полоса пропускания контура определяется на уровне 0,7 от максимальной амплитуды, которая есть на частоте резонанса.

Теперь перейдем к практике. Предположим нам нужно сделать параллельный контур, имеющий резонанс на частоте 1 МГц. Прежде всего нужно сделать предварительный расчет такого контура. То есть, определить необходимую емкость конденсатора и индуктивность катушки. Для предварительного расчета есть упрощенная формула:

L=(159,1/F)2/C где: L – индуктивность катушки в мкГн; С – емкость конденсатора в пФ; F – частота в МГц

Зададимся частотой 1 МГц и емкостью, к примеру, 1000 пФ. Получим:

L=(159,1/1)2 /1000 = 25 мкГн

Таким образом, если мы захотим контур на частоту 1 МГц, то нужен конденсатор на 1000 пФ и индуктивность на 25 мкГн. Конденсатор можно подобрать,, а вот индуктивность нужно сделать самостоятельно.

Рассчитать число витков для катушки без сердечника можно по такой формуле:

N=32 *√(L/D) где: N – требуемое число витков; L – заданная индуктивность в мкГн; D – диаметр каркаса в мм, на котором предполагается намотать катушку.

Предположим, диаметр каркаса – 5 мм, тогда:

N=32*√(25/5) = 72 витка.

Данная формула является приближенной, она не учитывает собственную межвитковую емкость катушки. Формула служит для предварительного вычисления параметров катушки, которые затем настраиваются при настройке контура.

В радиолюбительской практике чаще используются катушки с подстроечными сердечниками из феррита, имеющими длину 12-14 мм и диаметр 2,5 – 3 мм. Такие сердечники, например, применяются в контурах телевизоров и приемников. Для предварительного расчета числа витков для такого сердечника есть другая приближенная формула:

N=8,5*√L , подставляем значения для нашего контура N=8,5*√25 = 43 витка. То есть, в таком случае на потребуется намотать на катушку 43 витка провода.

Резонанс токов

Итак, давайте допустим, мы вогнали наш колебательный контур в резонанс:

Чему будет равняться резонансный ток Iрез ? Считаем по закону Ома:

Iрез = Uген /Rрез , где Rрез = L/CR.

Но самый прикол в том, что у нас при резонансе в контуре появляется свой собственный контурный ток Iкон , который не выходит за пределы контура и остается только в самом контуре! Так как с математикой у меня туго, поэтому я не буду приводить различные математические выкладки с производными и комплексными числами и объяснять откуда берется контурный ток при резонансе. Именно поэтому резонанс параллельного колебательного контура называется резонансом токов.

Добротность параллельного колебательного контура

Кстати, этот контурный ток будет намного больше, чем ток, который проходит через контур. И знаете во сколько раз? Правильно, в Q раз. Q — это и есть добротность! В параллельном колебательном контуре она показывает во сколько раз сила тока в контуре Iкон больше сила тока в общей цепи Iрез

Или формулой:

Если сюда еще прилепить сопротивление потерь, то формула примет вот такой вид:

где

Q — добротность

R — сопротивление потерь на катушке, Ом

С — емкость, Ф

L — индуктивность, Гн