Методы расчета простых и сложных разветвленных цепей постоянного тока.

Для вычисления рабочих параметров радиотехнических устройств и отдельных схем применяют специальные методики. После изучения соответствующих технологий результат можно узнать быстро, без сложных практических экспериментов. Корректный расчет электрических цепей пригодится на стадии проектирования и для выполнения ремонтных работ.

Категории элементов и устройств электрической цепи

Для условного изображения определенной цепи применяют специальную схему. Кроме отдельных физических компонентов, она содержит сведения о направлении (силе) токов, уровнях напряжения и другую информацию. Качественная модель показывает реальные процессы с высокой точностью.

Компоненты электрической цепи:

• источник постоянного или переменного тока (Е) – аккумулятор или генератор, соответственно;
• пассивные элементы (R) – резисторы;
• компоненты с индуктивными (L) и емкостными (С) характеристиками;
• соединительные провода.

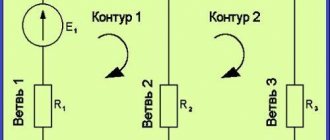
На рисунке обозначены:

• ветви – участки цепи с одним током;
• узлы – точки соединения нескольких ветвей;
• контур – замкнутый путь прохождения тока.

При решении практических задач выясняют, как узнать силу тока в отдельных ветвях. Полученные значения используют для анализа электрических параметров. В частности, можно определять падение напряжения на резисторе, мощность потребления подключенной нагрузки. При расчете цепей переменного тока приходится учитывать переходные энергетические процессы, влияние частоты.

Расчет потенциальной диаграммы

Содержание:

Потенциальная диаграмма

По результатам расчета электрической цепи для любого ее контура (ветви) можно построить потенциальную диаграмму — график распределений потенциала в контуре (ветви). При выбранной шкале на горизонтальной оси значения сопротивления резисторов (ответвлений) схемы располагаются в порядке (ответвлениях), расположенных в цепи, а вдоль вертикальной оси — потенциал (ответвление) в соответствующей точке цепи. Построение диаграммы можно начинать с любой точки контура, приравняв ее потенциал произвольной величине (например, нулю). Направление обхода контура (ветви) выбирается произвольно.

Пример:

Построим потенциальную диаграмму для внешнего контура электрической цепи, схема которой изображена на рис. 2. При построении диаграммы используем значения токов, рассчитанные в примере 2. Обход контура выбираем по часовой стрелке.

Приравняем потенциал точки 4 нулю. Потенциал точки 3 определяется из следующих соображений: при движении от точки 4 к точке 3 направление обхода контура совпадает с направлением тока 14 , а так как ток в ветви течет от большего потенциала к меньшему, потенциал точки 3 будет ниже потенциала точки 4 на величину падения напряжения на резисторе R4, следовательно

В результате расчета потенциал точки 3 оказался выше потенциала точки 4, так как выбранное на схеме направление тока противоположно его истинному направлению.

Аналогично определим потенциал точки 5: Потенциал точки I выше потенциала точки 5 на величину ЭДС Е1, так как направление обхода контура совпадает с направлением ЭДС (переход от отрицательного зажима источника ЭДС к его положительному зажиму), следовательно

Аналогичным образом определяются потенциалы точек 2 и 4:

Расчет потенциала точки 4 выполнен для проверки вычислений. Суммарное сопротивление резисторов контура

Зная максимальное и минимальное значения потенциалов точек и суммарное сопротивление резисторов контура, можно выбрать масштабы для потенциалов и сопротивления, а затем построить потенциальную диаграмму (рис. 3).

Возможно вам будут полезны данные страницы:

По потенциальной диаграмме можно определить потенциал любой точки контура, эквипотенциальные точки контура, а также разность потенциалов (напряжение) между любыми точками контура. Для определения напряжения заданные точки проецируются на ось ординат; умножив отрезок между проекциями точек на масштаб по напряжению, получим разность потенциалов.

Расчет и построение потенциальной диаграммы

Обозначим на схеме рис. 6 реальные направления токов и ЭДС внешнего контура. Примем потенциал точки (1) равным нулю, т.с.

Рассчитаем потенциалы всех точек, обходя контур по часовой стрелке (рис. 6).

Замечание. Источник тока учтен при расчете тока . Поэтому в схему рис.6 ЭДС не включаем.

Выберем масштаб по напряжению и сопротивлению:

По оси абсцисс откладываем сопротивления вдоль контура, начиная с точки (1), по оси ординат — потенциалы.

Под потенциальной диаграммой понимают график распределения потенциала вдоль какого — либо участка цепи или замкнутого контура. По оси абсцисс на нем откладывают сопротивления участков цепи друг за другом в том порядке, в каком они следуют на схеме, а по оси ординат — потенциалы отдельных точек цепи от нуля. Для определения потенциалов обычно потенциал одной из точек принимают равным нулю (то есть считают эту точку заземленной).

Пример построения потенциальной диаграммы

Условия расчета

Построить потенциальную диаграмму для контура цепи, изображенной на рисунке 4.5.2.1.

Схема контура цепи

Рисунок 10.1.2.1 — Схема контура цепи для построения потенциальной диаграммы

Данные для расчета потенциальной диаграммы

Токи найдены в предварительных расчетах всей цепи.

Расчет потенциальной диаграммы

Точку f заземлим, т.е. примем потенциал этой точки равным нулю, . При построении потенциальной диаграммы эту точку поместим в начало координат (см. рисунок 10.1.5.1).

Обход контура принимаем по направлению движения часовой стрелки, начиная с точки f

Подсчитываем потенциалы отдельных точек контура

Построение потенциальной диаграммы

Выбираем масштабы сопротивлений и потенциалов:

По полученным данным (п. 10.1.4) строим потенциальную диаграмму (см. рисунок 10.1.5.1) контура , изображенного на рисунке 10.1.2.1.

Чем больше ток в том или ином пассивном участке цепи, тем круче получается соответствующий участок диаграммы. Тангенсы углов наклона к оси абсцисс пропорциональны соответствующим токам, например,

Потенциальная диаграмма позволяет найти напряжение между любыми точками на схеме. Это напряжение равно разности ординат соответствующих точек диаграммы. Например, (см. рисунок 10.1.5.1).

На странице -> решение задач по электротехнике собраны решения задач и заданий с решёнными примерами по всем темам теоретических основ электротехники (ТОЭ).

Услуги:

Присылайте задания в любое время дня и ночи в whatsapp.

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназачен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Метод расчета по законам Ома и Кирхгофа

До изучения технологий вычислений необходимо уточнить особенности типовых элементов при подключении к разным источникам питания. При постоянном токе сопротивлением индуктивности можно пренебречь. Конденсатор эквивалентен разрыву цепи. Также следует учитывать следующие различия разных видов соединений резисторов:

• последовательное – увеличивает общее сопротивление;
• параллельное – распределяет токи по нескольким ветвям, что улучшает проводимость.

Закон Ома для участка цепи

Дифференциальный автомат надежная защита электрических цепей и человека

Типовая аккумуляторная батарея легкового автомобиля вырабатывает напряжение U = 12 V. Бортовой или внешний амперметр покажет соответствующее значение при измерении. Соединение клемм проводом недопустимо, так как это провоцирует короткое замыкание. Если жила тонкая (< 1 мм), высокая плотность тока в соответствующем поперечном сечении быстро увеличит температуру вплоть до теплового разрушения материала с разрывом цепи. Этот пример демонстрирует функциональность обычного плавкого предохранителя.

Подключив нагрузку, можно мультиметром проверить напряжение. Значение этого параметра остается неизменным. Если известно сопротивление (пример – R = 50 Ом), применение закона Ома (I = U/ R) поможет рассчитать ток:

I = 12/ 50 = 0,24 А.

По вычисленному значению с использованием формулы быстро определяется мощность:

P = I2 *R = U2/ R = 0,0576 * 50 = 2,88 Вт.

К сведению. Результат показанного расчета пригодится для поиска подходящего резистора. Следует делать запас в сторону увеличения. По стандарту серийных изделий подойдет элемент с паспортной номинальной мощностью 5 Вт.

На практике приходится решать более сложные задачи. Так, при значительной длине линии нужно учесть влияние соединительных ветвей цепи. Через стальной проводник ток будет протекать хуже, по сравнению с медным аналогом. Следовательно, надо в расчете учитывать удельное сопротивление материала. Короткий провод можно исключить из расчета. Однако в нагрузке может быть два элемента. В любом случае общий показатель эквивалентен определенному сопротивлению цепи. При последовательном соединении Rэкв = R1 + R2 +…+ Rn. Данный метод пригоден, если применяется постоянный ток.

Закон Ома для полной цепи

Для вычисления такой схемы следует добавить внутреннее сопротивление (Rвн) источника. Как найти ток, показывает следующая формула:

I = U/ (Rэкв + Rвн).

Вместо напряжения (U) при расчетах часто используют типовое обозначение электродвижущей силы (ЭДС) – E.

Первый закон Кирхгофа

По классической формулировке этого постулата алгебраическая сумма токов, которые входят и выходят из одного узла, равна нулю:

I1 + I2 + … + In = 0.

Это правило действительно для любой точки соединения ветвей электрической схемы. Следует подчеркнуть, что в данном случае не учитывают характеристики отдельных элементов (пассивные, реактивные). Можно не обращать внимания на полярность источников питания, включенных в отдельные контуры.

Чтобы исключить путаницу при работе с крупными схемами, предполагается следующее использование знаков отдельных токов:

• входящие – положительные (+I);
• выходящие – отрицательные (-I).

Второй закон Кирхгофа

Этим правилом установлено суммарное равенство источников тока (ЭДС), которые включены в рассматриваемый контур. Для наглядности можно посмотреть, как происходит распределение контрольных параметров при последовательном подключении двух резисторов (R1 = 50 Ом, R2 = 10 Ом) к аккумуляторной батарее (Uакб = 12 V). Для проверки измеряют разницу потенциалов на выводах пассивных элементов:

• UR1 = 10 V;
• UR1 = 2 V;
• Uакб = 12 V = UR1 + UR2 = 10 + 2;
• ток в цепи определяют по закону Ома: I = 12/(50+10) = 0,2 А;
• при необходимости вычисляют мощность: P = I2 *R = 0,04 * (50+10) = 2,4 Вт.

Второе правило Кирхгофа действительно для любых комбинаций пассивных компонентов в отдельных ветвях. Его часто применяют для итоговой проверки. Чтобы уточнить корректность выполненных действий, складывают падения напряжений на отдельных элементах. Следует не забывать о том, что дополнительные источники ЭДС делают результат отличным от нуля.

Метод преобразования электрической цепи

Расчет мощности

Как определить силу тока в отдельных контурах сложных схем? Для решения практических задач не всегда нужно уточнение электрических параметров на каждом элементе. Чтобы упростить вычисления, используют специальные методики преобразования.

Расчет цепи с одним источником питания

Для последовательного соединения пользуются рассмотренным в примере суммированием электрических сопротивлений:

Rэкв = R1 + R2 + … + Rn.

Контурный ток – одинаковый в любой точке цепи. Проверять его можно в разрыве контрольного участка мультиметром. Однако на каждом отдельном элементе (при отличающихся номиналах) прибор покажет разное напряжение. По второму закону Кирхгофа можно уточнить результат вычислений:

E = Ur1 + Ur2 + Urn.

В этом варианте в полном соответствии с первым постулатом Кирхгофа токи разделяются и соединяются во входных и выходных узлах. Показанное на схеме направление выбрано с учетом полярности подключенного аккумулятора. По рассмотренным выше принципам сохраняется базовое определение равенства напряжений на отдельных компонентах схемы.

Как найти ток в отдельных ветвях, демонстрирует следующий пример. Для расчета приняты следующие исходные значения:

• R1 = 10 Ом;
• R2 = 20 Ом;
• R3= 15 Ом;
• U = 12 V.

По следующему алгоритму будут определяться характеристики цепи:

• базовая формула для трех элементов:

Rобщ = R1*R2*R3/(R1*R2 + R2*R3 + R1*R3.

• подставив данные, вычисляют Rобщ = 10 * 20 * 15 / (10*20 + 20*15 +10*15) = 3000 /(200+300+150) = 4,615 Ом;
• I = 12/ 4,615 ≈ 2,6 А;
• I1 = 12/ 10 = 1,2 А;
• I2 = 12/20 = 0,6 А;
• I3 = 12/15 = 0,8 А.

Как и в предыдущем примере, рекомендуется проверить результат вычислений. При параллельном соединении компонентов должно соблюдаться равенство токов на входе и суммарного значения:

I = 1,2 + 0,6 + 0,8 = 2,6 А.

Если применяется синусоидальный сигнал источника, вычисления усложняются. При включении в однофазную розетку 220V трансформатора придется учитывать потери (утечку) в режиме холостого хода. В этом случае существенное значение имеют индуктивные характеристики обмоток и коэффициент связи (трансформации). Электрическое сопротивление (ХL) зависит от следующих параметров:

• частоты сигнала (f);
• индуктивности (L).

Вычисляют ХL по формуле:

ХL = 2π * f * L.

Чтобы находить сопротивление емкостной нагрузки, подойдет выражение:

Хc = 1/ 2π * f * C.

Следует не забывать о том, что в цепях с реактивными компонентами сдвигаются фазы тока и напряжения.

Расчет разветвленной электрической цепи с несколькими источниками питания

Пользуясь рассмотренными принципами, вычисляют характеристики сложных схем. Ниже показано, как найти ток в цепи при наличии двух источников:

• обозначают компоненты и базовые параметры во всех контурах;
• составляют уравнения для отдельных узлов: a) I1-I2-I3=0, b) I2-I4+I5=0, c) I4-I5+I6=0;
• в соответствии со вторым постулатом Кирхгофа, можно записать следующие выражения для контуров: I) E1=R1 (R01+R1)+I3*R3, II) 0=I2*R2+I4*R4+I6*R7+I3*R3, III) -E2=-I5*(R02+R5+R6)-I4*R4;
• проверка: d) I3+I6-I1=0, внешний контур E1-E2=I1*(r01+R1)+I2*R2-I5*(R02+R5+R6)+I6*R7.

Потенциал электрического поля

Важным свойством электрического поля, как поля не имеющего вихрей и созданного одними неподвижными источниками, является его потенциальность

Электрическое поле называется потенциальным, если работа, которую совершает носитель заряда в таком поле, при перемещении его по любому замкнутому контуру равняется нулю.

Гравитационное поле силы тяжести также является потенциальным

Если поднять груз определенной массы на некоторую высоту, а затем опустить его обратно на поверхность Земли, в прежнюю точку, то полная механическая работа будет также равна нулю.

Причем, совершенно не важно по какой траектории осуществлялся подъем и спуск груза. Источником такого гравитационного поля является в этом примере Земля (тело с массой во много раз большей чем масса поднимаемого груза).

Дополнительные методы расчета цепей

Подключение светодиода через резистор и его расчет

В зависимости от сложности устройства (электрической схемы), выбирают оптимальную технологию вычислений.

Метод узлового напряжения

Основные принципы этого способа базируются на законе Ома и постулатах Кирхгофа. На первом этапе определяют потенциалы в каждом узле. Далее вычисляют токи в отдельных ветвях с учетом соответствующих электрических сопротивлений (отдельных компонентов или эквивалентных значений). Проверку делают по рассмотренным правилам.

Метод эквивалентного генератора

Эта технология подходит для быстрого расчета тока в одной или нескольких контрольных ветвях.

В данной методике общую цепь представляют в виде источника тока с определенным напряжением и внутренним сопротивлением. Далее выполняют вычисления по контрольной ветви с применением стандартного алгоритма.