ТОЭ › Расчет цепей постоянного тока
При расчете режима работы электрической цепи очень часто необходимо определить токи, напряжения и мощности на всех ее участках при заданных ЭДС источников и сопротивлений участков цепи. Данный расчёт основан на применении законов Кирхгофа.
В этой статье предполагается, что вы знакомы с определениями узла, ветви и контура.
Первый закон Кирхгофа
Первый закон Кирхгофа гласит, что в ветвях образующих узел электрической цепи алгебраическая сумма токов равна нулю (токи входящие в узел считаются положительными, выходящие из узла отрицательными).
Пользуясь этим законом для узла A (рисунок 1) можно записать следующее выражение:
Рисунок 1 — Первый закон Кирхгофа
I1 + I2 − I3 + I4 − I5 − I6 = 0.
Попытайтесь самостоятельно применить первый закон Кирхгофа для определения тока в ветви. На приведенной выше схеме изображены шесть ветвей образующие электрический узел В, токи ветвях входят и выходят из узла. Один из токов i неизвестен.
#1. Запишите выражение для узла В
Неправильно
Далее
#2. Найдите ток i
Неправильно
Завершить
Закон Ома
Ток, напряжение и сопротивление связаны напрямую с законом Ома, описывающим отношение напряжения (приложенного к элементу) к заданному сопротивлению, в результате которого протекает ток.
| Помните, что мы всегда обозначаем эти значения следующим образом: U — напряжение, R — сопротивление, I — ток. |
Вы очень часто придется встречаться с этим законом в области электроники. К счастью, вам не нужно учить этот закон наизусть, т.к. в простейшей форме оно выражается тремя простыми формулами, которые для удобства использования обычно записываются в виде треугольника, как на картинке ниже:
| На самом деле это один паттерн (шаблон), трансформируется по мере необходимости. Достаточно запомнить одну из формул (например, U = I * R), чтобы в любой момент преобразовать ее в другую. |
Результат
Отлично!
Попытайтесь снова(
Выбор направления токов
Если при расчёте цепи направление токов неизвестны, то при составлении уравнений согласно законом Кирхгофа их необходимо предварительно выбрать произвольно и обозначить на схеме стрелками. В действительности направление токов в ветвях могут отличаться от произвольно выбранных. Поэтому выбранные направления токов называют положительными направлениями. Если в результате расчёта цепи какие-либо токи будут выражены отрицательными числами, то действительные направления этих токов обратны выбранным положительным направлениям.
Например
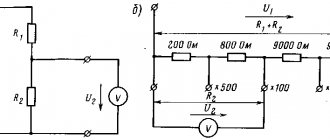
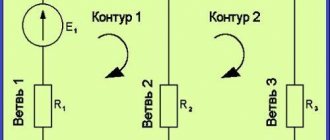
Рисунок 2
На рисунке 2,а представлен электрический узел. Произвольно, стрелками укажем направления токов (рисунок 2,б).
Важно! При выборе направления токов в ветвях, необходимо выполнения двух условий: 1. Ток должен вытекать из узла через одну или несколько других ветвей; 2. Хотя бы один ток должен входить в узел.
Предположим, что после расчёта цепи получились следующие значения токов:
I1 = -5 А; I2 = -2 A; I3 = 3 А.
Так как значение тока I1 и I2 получились отрицательными, следовательно, действительно направление I1 и I2 противоположно ранее выбранным (рисунок 3).
Рисунок 3 — действительное направление токов обозначено синими стрелками
- I1 − I2 + I3 = 0;
- -5 − (-2) +3 = 0;
- -I1 + I2 + I3 = 0;
- -5 + 2 +3 = 0.
Учебные материалы
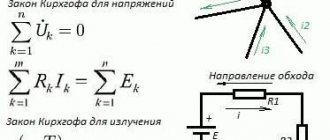
Согласно первому закону Кирхгофа алгебраическая сумма токов ветвей, сходящихся в узле, равна нулю:
Согласно второму закону Кирхгофа алгебраическая сумма напряжений на резистивных элементах замкнутого контура равна алгебраической сумме ЭДС, входящих в этот контур.
Получить решение по ТОЭ
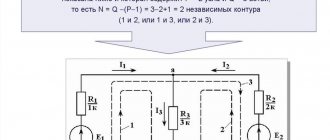
Расчет многоконтурной линейной электрической цепи, имеющей «b» ветвей с активными и пассивными элементами и «у» узлов, сводится к определению токов отдельных ветвей и напряжений на зажимах элементов, входящих в данную цепь.
Пассивной называется ветвь, не содержащая источника ЭДС. Ветвь, содержащая источник ЭДС, называется активной.
1-й закон Кирхгофа применяют к независимым узлам, т.е. таким, которые отличаются друг от друга хотя бы одной новой ветвью, что позволяет получить (y — I) уравнений.
Недостающие уравнения в количестве b — (у — I) составляют, исходя из второго закона Кирхгофа. Уравнение записывают для независимых контуров, которые отличаются один от другого, по крайней мере, одной ветвью.
Порядок выполнения расчета:
- выделяют в электрической цепи ветви, независимые узлы и контуры;
- с помощью стрелок указывают произвольно выбранные положительные направления токов в отдельных ветвях, а также указывают произвольно выбранное направление обхода контура;
- составляют уравнения по законам Кирхгофа, применяя следующее правило знаков:
- токи, направленные к узлу цепи, записывают со знаком «плюс», а токи, направленные от узла,- со знаком «минус» (для первого закона Кирхгофа);
- ЭДС и напряжение на резистивном элементе (RI) берутся со знаком»плюс», если направления ЭДС и тока в ветви совпадают с направлением обхода контура, а при встречном направлении — со знаком «минус»;
Отрицательные значения тока какой-либо ветви указывают на то, что выбранные ранее произвольные направления тока оказались ошибочными. Это следует учитывать, например, при построении потенциальной диаграммы, где следует знать истинное направление тока.
На рис. 4, а изображена исходная электрическая схема, для которой следует рассчитать токи в ветвях. Направления токов и обхода контуров приведены на рис. 4, б.
Рис.4
Система уравнений, составленных по первому и второму законам Кирхгофа, имеет вид
Дальше >Лекции по основам электротехники >
Интерпретация закона Ома
Что касается тока, то закон Ома говорит, что он прямо пропорционален напряжению. Например, если мы увеличим напряжение в 10 раз, ток также возрастет в 10 раз. Это видно из формулы I = U / R (чем выше будет напряжение, тем выше будет ток).
Если сравнить с водой, то на картинке хорошо видно: при повышении уровня воды (повышается напряжение) из плотины вытекает больше воды (увеличивается ток).
I ~ U
Как видите, есть возрастающее напряжение (уровень воды) с постоянным сопротивлением (положение шлюза в дамбе). Вывод: увеличение напряжения приводит к протеканию большего тока при том же сопротивлении.
| I ~ U здесь означает, что ток прямо пропорционален напряжению. |
Рассмотрим другой пример. На этот раз уровень воды (напряжение) будет постоянным. Изменится только степень открытия шлюза в дамбе (сопротивление):
I ~ 1 / R
На этот раз мы можем заметить, что при постоянном напряжении, ток, протекающий через данный элемент, зависит от его сопротивления. Вывод: ток обратно пропорционален сопротивлению (чем меньше сопротивление, тем больше тока будет протекать в цепи).
| Обозначение I ~ 1 / R здесь означает, что ток обратно пропорционален сопротивлению. |
Применим на практике закон Ома
Проверим на практике, действительно ли «работает» закон Ома. Возьмем батарейку или аккумулятор напряжением около 9 вольт. Нам нужно узнать, какой ток будет протекать, если мы замкнем цепь, подключив к ней резистор 10 кОм. Кружок с надписью «mA» на схеме обозначает наш мультиметр (тестер), настроенный на измерение амперов.
Вначале проверяем теоретически. Для этого используем известные нам формулы:
U = 9 В, R = 10 кОм , I =?
I = U / R = 9 В / 10000 Ом = 0,0009 A = 0,9 мА
Значит тестер нам должен показать около 0,9 мА . Теперь соберите данную схему на макетной плате. В случае возникновения проблем вы можете использовать пример ниже. Просто будьте осторожны, чтобы не допустить короткого замыкания в цепи при установке компонентов, при замыкании можно повредить аккумулятор.
| Не забудьте правильно настроить мультиметр при измерении тока! |
Результат измерения в указанной выше цепи составляет 0,95 мА . Почему по расчетам у нас получилась одна цифра, а на практике, после измерения тестером, другая? Не следует забывать, что измерения имеют погрешность. Как вы помните, из предыдущей статьи, все резисторы имеют погрешность около 5%, также, сопротивление щупов и самого мультиметра, и к тому же, батарея или аккумулятор может быть не заражена на все 9В! В среднем получается, что результат верный!
Теперь, для теста, нам нужно проверить, что произойдет, если мы подключим другой резистор, а именно 1 кОм , вместо резистора 10 кОм. Держа в голове закон Ома, мы уже должны предугадать, что подключение резистора с в 10 раз меньшим сопротивлением должно давать в 10 раз больший ток. Проверим:
Читать также: Источники опорного напряжения
Что такое делитель напряжения?
Делитель напряжения — не что иное, как одно из практических применений вышеуказанных законов. На практике все очень просто — последовательно соединяем два резистора и запитываем их.
Напряжение на ножках каждого из них будет пропорционально меньше, но их сумма будет равна напряжению питания. Это не что иное, как иллюстрация действия второго закона Кирхгофа. Другими словами, эта система позволяет разделить напряжение питания, благодаря чему, мы можем получить, например, 6В от батареи 9В.
Читать также: Что такое ПЛИС?
Это описывается следующей формулой:
Uвход — это напряжение, питающее наш делитель. В числитель ставится номинал резистора, на котором мы хотим узнать падение напряжения. Знаменатель — это сумма обоих сопротивлений. Такое подключение мы уже производили, поэтому повторяться сейчас не будем — самое главное запомнить формулу, которая позволяет рассчитать напряжение, которое должно появиться на резисторе.
Например, посчитаем значение напряжения, которое мы получаем на делителе, состоящем из резисторов 1 кОм и 220 Ом, питаемый от 3 В. Схема будет выглядеть так:
В этом случае расчет напряжения Uвыход будет выглядеть так:
Теперь сделайте свои собственные расчеты для делителя напряжения, состоящего из резисторов 1 кОм и 330 Ом, питаемых батарекой 9 В. Рассчитайте Uвыход на резисторе 1 кОм. Соберите такую схему самостоятельно на макетной плате и измерьте напряжение. В случае проблем вернитесь к примеру выше.
Что такое внутреннее сопротивление?
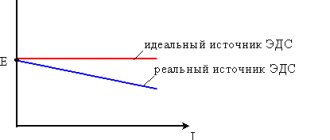
Внутреннее сопротивление — это параметр, который является общим для каждого источника питания, но о нем часто забывают. Любой реальный источник напряжения можно в простейшем случае смоделировать, как последовательную комбинацию идеального источника и определенного сопротивления.
| Проще всего представить, батарейку или аккумулятор, внутри которого, есть резистор. |
Такое сопротивление никому не нужно, но с этим ничего не поделать; производители могут только стараться поддерживать это сопротивление на минимально возможном уровне. Это связано с составом контактных сопротивлений, крышек батарей, выводов и т.д. Кроме того, сопротивление может зависеть от температуры, сроков эксплуатации элементов и других факторов.
Это сопротивление нельзя точно самим рассчитать и не пытайтесь измерить его мультиметром! Такую информацию может предоставить только производитель батареи. К счастью, это для нас сейчас не важно, самое главное — просто знать о существовании внутреннего сопротивления.
Наличие внутреннего сопротивления иллюстрирует очень простой опыт. Давайте измерим напряжение в цепи, при течении тока через резисторы 1 кОм и 10 кОм и без них. Вот очень простая схема измерения:
Примеры измерений:
| Резистор 1k подключен | Резистор 10 кОм подключен | Без резистора |
Как вы можете видеть в приведенном выше примере, увеличивая ток от батареи, мы получаем более низкое напряжение. Это можно прекрасно объяснить так: чем меньше R1 (который представляет собой нагрузку) по сравнению с R2 (которое представляет собой внутреннее сопротивление), тем большее напряжение подается на R2. Для многих измерение без резистора может вызывать недоумение, потому что они думают, что это означает отсутствие сопротивления — это неправильное мышление.
| Отсутствие резистора следует понимать как бесконечно большое сопротивление. Так как, в цепи не протекает ток и батарея никак не нагружается, поэтому измеренное напряжение является самым высоким. |
Помните, что при зарядке аккумулятора слишком большим током (через резистор с низким сопротивлением), аккумулятор может нагреться и выйти из строя (может произойти утечка электролита)! При потреблении большого тока, используйте источник с достаточно низким внутренним сопротивлением и достаточно большой мощностью.
| Вышеупомянутый феномен беспокоит многих новичков, пытающихся запитать свои проекты небольшими батареями (например, 9 В). Они забывают, что высокое потребление тока (например, моторами) вызывает падение напряжения на батарее. Это может помешать работе всей системы. |