Электрический ток
Электрический ток (I) это направленное движение свободных носителей электрического заряда. В металлах свободными носителями заряда являются электроны, в плазме, электролите — ионы.
Единица измерения силы тока – ампер (А). Условно за положительное направление тока во внешней цепи принимают направление от положительно заряженного электрода (+) к отрицательно заряженному (-).
Получить решение по ТОЭ
Если направление тока в ветви неизвестно, то его выбирают произвольно. Если в результате расчета режима цепи, ток будет иметь отрицательное значение, то действительное направление тока противоположно произвольно выбранному.
Угловая (циклическая) частота переменного тока.
Скорость вращения радиуса-вектора, т. е. изменение величины угла поворота в течение одной секунды, называется угловой (циклической) частотой переменного тока и обозначается греческой буквой ? (омега). Угол поворота радиуса-вектора в любой данный момент относительно его начального положения измеряется обычно не в градусах, а в особых единицах — радианах.
Радианом называется угловая величина дуги окружности, длина которой равна радиусу этой окружности (рисунок 2). Вся окружность, составляющая 360°, равна 6,28 радиан, то есть 2
.
Рисунок 2. Радиан.
1рад = 360°/2
? = 6,28*f = 2f
Электродвижущая сила
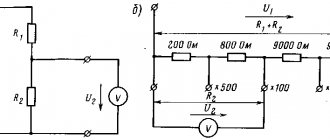
Электродвижущая сила Е (ЭДС) характеризует способность индуцированного поля вызывать электрический ток. Единица измерения – вольт (В). Источники энергии могут быть источниками ЭДС и тока. В данном пособии рассматриваются только источники ЭДС. Источник ЭДС характеризуется двумя параметрами: значениями ЭДС (Е) и внутреннего сопротивления (r0). Источник ЭДС, внутренним сопротивлением которого можно пренебречь, называют идеальным источником. Реальный источник ЭДС имеет определенное значение внутреннего сопротивления. У источника ЭДС внутренне сопротивление значительно меньше сопротивления нагрузки (RН) и электрический ток в цепи зависит главным образом от величины ЭДС и сопротивления нагрузки. Источник ЭДС имеет следующие графические обозначения.
Вольтамперная характеристика источника ЭДС имеет вид:
Рис. 1
Зависимость между напряжением на зажимах источника и его ЭДС имеет вид:
U = E — r0× I (для реального источника ЭДС)
U = E (для идеального источника).
Электрическое сопротивление R это величина, характеризующая противодействие проводящей среды движению свободных электрических зарядов (току). Единица измерения – Ом. Величина, обратная сопротивлению, называется электрической проводимостью G. Единица измерения – сименс (См).
Период и частота переменного тока
Время, в течение которого совершается одно полное изменение ЭДС, то есть один цикл колебания или один полный оборот радиуса-вектора, называется периодом колебания переменного тока (рисунок 1).
Период выражают в секундах и обозначают буквой Т.
Так же используются более мелкие единицы измерения периода это миллисекунда (мс)- одна тысячная секунды и микросекунда (мкс)- одна миллионная секунды.
Число полных изменений ЭДС или число оборотов радиуса-вектора, то есть иначе говоря, число полных циклов колебаний, совершаемых переменным током в течение одной секунды, называется частотой колебаний переменного тока.
Частота обозначается буквой f и выражается в периодах в секунду или в герцах.
Одна тысяча герц называется килогерцом (кГц), а миллион герц — мегагерцом (МГц). Существует так же единица гигагерц (ГГц) равная одной тысячи мегагерц.
1000 Гц = 10 3 Гц = 1 кГц;
1000 000 Гц = 10 6 Гц = 1000 кГц = 1 МГц;
1000 000 000 Гц = 10 9 Гц = 1000 000 кГц = 1000 МГц = 1 ГГц;
Чем быстрее происходит изменение ЭДС, то есть чем быстрее вращается радиус-вектор, тем меньше период колебания Чем быстрее вращается радиус-вектор, тем выше частота. Таким образом, частота и период переменного тока являются величинами, обратно пропорциональными друг другу. Чем больше одна из них, тем меньше другая.
Математическая связь между периодом и частотой переменного тока и напряжения выражается формулами
Например, если частота тока равна 50 Гц, то период будет равен:
Т = 1/f = 1/50 = 0,02 сек.
И наоборот, если известно, что период тока равен 0,02 сек, (T=0,02 сек.), то частота будет равна:
f = 1/T=1/0,02 = 100/2 = 50 Гц
Частота переменного тока, используемого для освещения и промышленных целей, как раз и равна 50 Гц.
Частоты от 20 до 20 000 Гц называются звуковыми частотами. Токи в антеннах радиостанций колеблются с частотами до 1 500 000 000 Гц или, иначе говоря, до 1 500 МГц или 1,5 ГГц. Такие высокие частоты называются радиочастотами или колебаниями высокой частоты.
Наконец, токи в антеннах радиолокационных станций, станций спутниковой связи, других спецсистем (например ГЛАНАСС, GPS) колеблются с частотами до 40 000 МГц (40 ГГц) и выше.
Проводниковые материалы
Проводниковые материалы (алюминий, медь, золото, серебро и др.) обладают высокой электропроводностью. Наиболее часто в проводах и кабелях используется алюминий, как наиболее дешевый. Медь имеет большую электропроводимость, но она дороже.
Из проводников следует выделить группу материалов с большим удельным сопротивлением. К ним относятся сплавы ( нихром, фехраль и др.) они используются для изготовления обмоток нагревательных приборов и реостатов. Вольфрам используется в лампах накаливания. Константан и манганин используются в качестве сопротивлений в образцовых приборах.
Электроизоляционные материалы (диэлектрики)
Электроизоляционные материалы (диэлектрики) имеют очень малую удельную электрическую проводимость. Они бывают газообразные, жидкие и твердые. Особенно большим разнообразием отличаются твердые диэлектрики. К ним относятся резина, сухое дерево, керамические материалы, пластмассы, картон, пряжа и др. материалы. В качестве конструкционных материалов применяются текстолит и гетинакс. Текстолит это диэлектрический материал основой которого является ткань, пропитанная феноло-формальдегидной смолой. Гетинакс это бумага, пропитанная феноло-формальдегидной смолой.
Полупроводники
Полупроводники по электропроводимости занимают промежуточное положение между проводниками и диэлектриками. Простые полупроводниковые вещества – германий, кремний, селен, сложные полупроводниковые материалы — арсенид галлия, фосфид галлия и др. В чистых полупроводниках концентрация носителей заряда – свободных электронов и дырок мала и эти материалы не проводят электрический ток.
Если в полупроводниковый материал ввести примесь (донорную или акцепторную), то есть произвести легирование, то полупроводник становится обладателем или электронной (n) проводимости (избыток электронов), или дырочной (р) проводимости (избыток положительных зарядов – дырок). Если соединить два полупроводника с различными видами проводимости, получим полупроводниковый прибор (диод), который используется для выпрямления переменного тока.
Мощность в электрической цепи характеризует интенсивность преобразования энергии из одного вида в другой в единицу времени. Единица измерения мощности – Ватт (Вт).
Для цепи постоянного тока мощность источника
Pист = E I.
Мощность приемника
Рпр = U × I = R × I2 = U2/R
Полное сопротивление цепи при параллельном соединении активного и реактивного элемента.
Для того чтобы вычислить полное сопротивление цепи, составленной из активного и индуктивного сопротивлений, соединенных между собой параллельно(рис. 5,а), нужно сначала вычислить проводимость каждой из параллельных ветвей, потом определить полную проводимость всей цепи между точками А и В и затем вычислить полное сопротивление цепи между этими точками.
Рисунок 5. Полное сопротивление цепи при параллельном соединении активного и реактивных элементов .
а) — параллельное соединение R и L; б) — параллельное соединение R и C
.
Проводимость активной ветви, как известно, равна 1/R, аналогично проводимость индуктивной ветви равна 1/ωL , а полная проводимость равна 1/Z
Полная проводимость равна корню квадратному из суммы квадратов активной и реактивной проводимости, т. е.
(7)
Приводя к общему знаменателю подкоренное выражение, получим:
(8)
(9)
Формула (9) служит для вычисления полного сопротивления цепи, изображенной на рис. 5а.
Нахождение полного сопротивления для этого случая может быть произведено и геометрическим путем. Для этого нужно построить в соответствующем масштабе треугольник сопротивлений, и затем произведение длин катетов разделить на длину гипотенузы. Полученный результат и будет соответствовать полному сопротивлению.
Аналогично случаю, рассмотренному выше, полное сопротивление при параллельном соединении R и С (рис 5б) будет равно:
(10)
Полное сопротивление может быть найдено также и в этом случае путем построения треугольника сопротивлений.
В радиотехнике наиболее часто встречается случай па¬раллельного соединения индуктивности и емкости, например колебательный контур для настройки приемников и передатчиков. Так как катушка индуктивности всегда обладает кроме индуктивного еще и активным сопротивлением, то эквивалентная (равноценная) схема колебательного контура будет содержать в индуктивной ветви активное сопротивление (рис 7).
Рисунок 6. Эквивалентная схема колебательного контура .
Формула полного сопротивления для этого случая будет:
(11)
Так как обычно активное сопротивление катушки (R) бывает очень мало по сравнению с ее индуктивным сопротивлением (ωL), то мы имеем право формулу (11) переписать в следующем виде:
(12)
В колебательном контуре обычно подбирают величины L и С таким образом, чтобы индуктивное сопротивление равнялось емкостному, т. е. чтобы соблюдалось условие
(13)
При соблюдении этого условия полное сопротивление колебательного контура будет равно:
(14)
где L-индуктивность катушки в Гн;
С-емкость конденсатора в Ф;
R-активное сопротивление катушки в Ом.
Данный раздел основных формул ТОЭ предназначен для начинающих, как для студентов высших учебных заведений изучающих курс физики по электротехники, так и просто для интересующихся общей электротехникой /ТОЭ/ с примерами и комментариями автора:
Прежде чем перейти к формулам, обращу Ваше внимание на буквенное обозначение в ТОЭ, в разных учебниках по ТОЭ, мягко говоря, обозначение довольно произвольное, нет единого требования по данному вопросу в электротехнике. Особенно заметна разность обозначения в комплексных числах (как грибы в лесу, как только их не называют в разных местностях). Поэтому определимся сразу с буквенным обозначением :