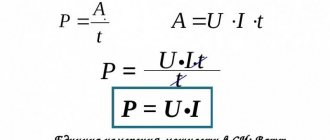Как найти массу Имея мощность высоту и время?

Содержание

Если на тело действует сила и оно движется, то совершается механическая работа. Мы знаем, что эта физическая величина зависит от приложенной силы и пройденного пути ($A = Fs$) и измеряется в джоулях.

Очевидно, что на совершение одной и той же работы в разных случаях уходит разное количество времени. Например, на девятый этаж дома нужно поднять шкаф. Если его загрузят в лифт, то работа будет выполнена за несколько секунд. А если грузчик будет поднимать шкаф пешком по лестнице? На выполнение такой работы уйдет гораздо больше времени.

Таким же образом грузовой автомобиль способен переместить груз определенной массы за один раз, тогда как легковому автомобилю придется съездить несколько раз до пункта назначения и обратно, чтобы доставить весь груз.

Так появляется новая физическая величина, позволяющая описать насколько быстро может быть выполнена та или иная работа.

Определение и формула работы

Определение

В том случае, если под воздействием силы происходит изменение модуля скорости движения тела, то говорят о том, что сила совершает работу

. Считают, что если скорость увеличивается, то работа является положительной, если скорость уменьшается, то работа, которую совершает сила – отрицательна. Изменение кинетической энергии материальной точки в ходе ее движения между двумя положениями равно работе, которую совершает сила:
$$A=\Delta E_{k}=\frac{m v_{2}^{2}}{2}-\frac{m v_{1}^{2}}{2}(1)$$
Действие силы на материальную точку можно охарактеризовать не только с помощью изменения скорости движения тела, но при помощи величины перемещения, которое совершает рассматриваемое тело под действием силы ($\bar{F}$).

Определение мощности

Быстроту выполнения работы характеризуют физической величиной, называемой мощность.

Мощность — это физическая величина, равная отношению работы ко времени, за которое она была совершена.

Чтобы вычислить мощность, нужно работу разделить на время, в течение которого совершена эта работа:

$$мощность = \frac{работа}{время}$$

или

$$N = \frac{A}{t}$$

где $N$ — мощность, $A$ — работа, $t$ — время выполнения работы.

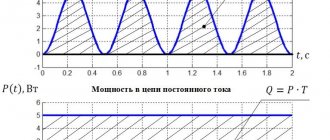
Мощность может быть:

1. Постоянной, если за каждую секунду совершается одинаковая работа
2. Непостоянной, если за каждую секунду совершается разная работа. В таком случае говорят о средней мощности: $N_{ср} = \frac{A}{t}$

Элементарная работа

Элментарная реабота $(\delta A)$ некоторой силы $\bar{F}$ определяется как скалярное произведение:

$$\delta A=\bar{F} \cdot d \bar{r}=F \cdot d s \cdot \cos \alpha(2)$$

$\bar{r}$ радиус – вектор точки, к которой приложена сила, $\bar{r}$ — элементарное перемещение точки по траектории, $\alpha$ – угол между векторами $d s=|d \bar{r}|$ и $d \bar{r}$. Если $\alpha$ является тупым углом работа меньше нуля, если угол $\alpha$ острый, то работа положительная, при $\alpha=\frac{\pi}{2} \delta A=0$

В декартовых координатах формула (2) имеет вид:

$$\delta A=F_{x} d x+F_{y} d y+F_{z} d z(3)$$

где Fx,Fy,Fz – проекции вектора $\bar{F}$ на декартовы оси.

При рассмотрении работы силы, приложенной к материальной точке можно использовать формулу:

$$\delta A=\bar{F} \bar{v} d t=\bar{v} d \bar{p}(4)$$

где $\bar{v}$ – скорость материальной точки, $\bar{p}$ – импульс материальной точки.

Если на тело (механическую систему) действуют несколько сил одновременно, то элементарная работа, которую совершают эти силы над системой, равна:

$$\delta A=\sum_{i=1}^{n} \delta A_{i}=\sum_{i=1}^{n} \bar{F}_{i} d \bar{r}_{i}=\sum_{i=1}^{n} \bar{F}_{i} \bar{v}_{i} d t(5)$$

где проводится суммирование элементарных работ всех сил, dt – малый промежуток времени, за который совершается элементарная работа $\delta$ над системой.

Результирующая работа внутренних сил, даже если твердое тело движется, равна нулю.

Пусть твердое тело вращается около неподвижной точки — начала координат (или неподвижной оси, которая проходит через эту точку). В таком случае, элементарная работа всех внешних сил (допустим, что их число равно n), которые действуют на тело, равна:

$$\delta A=\bar{M} \bar{\omega} d t=\bar{M} d \bar{\varphi}(6)$$

где $\bar{M}$ – результирующий момент сил относительно точки вращения, $d \bar{\varphi}$ – вектор элементарного поворота, $\bar{w}$ – мгновенная угловая скорость.

Единица измерения мощности

За единицу мощности принимают такую мощность, при которой за 1 с совершается работа в 1 Дж.

Эта единица называется ваттом (Вт) в честь ученого Уатта (рисунок 1).

Из формулы мощности $N = \frac{A}{t}$:

$$1 \space ватт = \frac{1 \space джоуль}{1 \space секунда} = 1 \frac{Дж}{с}$$

Часто используются другие единицы мощности — киловатт (кВт), мегаватт (МВт) и милливатт (мВт):

$1 \space МВт = 1 000 000 \space Вт$

$1 \space Вт = 0.000001 МВт$

$1 \space кВт = 1000 \space Вт$

$1 \space Вт = 0.001 кВт$

$1 \space мВт = 0.001 \space Вт$

$1 \space Вт = 1000 \space мВт$

Также мощность иногда измеряют в лошадиных силах (л. с.):

$1 \space л. с. = 735.5 \space Вт$

$1 \space Вт = 0.00013596 \space л.с.$

Эта единица измерения не так популярна как ватт, но до сих пор используется, например, в автомобильной индустрии.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. Работа определяется по формуле

1) ​\( A=Fv \)​ 2) \( A=N/t \)​ 3) \( A=mv \)​ 4) \( A=FS \)​

2. Груз равномерно поднимают вертикально вверх за привязанную к нему верёвку. Работа силы тяжести в этом случае

1) равна нулю 2) положительная 3) отрицательная 4) больше работы силы упругости

3. Ящик тянут за привязанную к нему верёвку, составляющую угол 60° с горизонтом, прикладывая силу 30 Н. Какова работа этой силы, если модуль перемещения равен 10 м?

1) 300 Дж 2) 150 Дж 3) 3 Дж 4) 1,5 Дж

4. Искусственный спутник Земли, масса которого равна ​\( m \)​, равномерно движется по круговой орбите радиусом ​\( R \)​. Работа, совершаемая силой тяжести за время, равное периоду обращения, равна

1) ​\( mgR \)​ 2) ​\( \pi mgR \)​ 3) \( 2\pi mgR \)​ 4) ​\( 0 \)​

5. Автомобиль массой 1,2 т проехал 800 м по горизонтальной дороге. Какая работа была совершена при этом силой трения, если коэффициент трения 0,1?

1) -960 кДж 2) -96 кДж 3) 960 кДж 4) 96 кДж

6. Пружину жёсткостью 200 Н/м растянули на 5 см. Какую работу совершит сила упругости при возвращении пружины в состояние равновесия?

1) 0,25 Дж 2) 5 Дж 3) 250 Дж 4) 500 Дж

7. Шарики одинаковой массы скатываются с горки по трём разным желобам, как показано на рисунке. В каком случае работа силы тяжести будет наибольшей?

1) 1 2) 2 3) 3 4) работа во всех случаях одинакова

8. Работа по замкнутой траектории равна нулю

А. Силы трения Б. Силы упругости

Верным является ответ

1) и А, и Б 2) только А 3) только Б 4) ни А, ни Б

9. Единицей мощности в СИ является

1) Дж 2) Вт 3) Дж·с 4) Н·м

10. Чему равна полезная работа, если совершённая работа составляет 1000 Дж, а КПД двигателя 40 %?

1) 40000 Дж 2) 1000 Дж 3) 400 Дж 4) 25 Дж

11. Установите соответствие между работой силы (в левом столбце таблицы) и знаком работы (в правом столбце таблицы). В ответе запишите выбранные цифры под соответствующими буквами.

РАБОТА СИЛЫ A. Работа силы упругости при растяжении пружины Б. Работа силы трения B. Работа силы тяжести при падении тела

ЗНАК РАБОТЫ 1) положительная 2) отрицательная 3) равна нулю

12. Из приведённых ниже утверждений выберите два правильных и запишите их номера в таблицу.

1) Работа силы тяжести не зависит от формы траектории. 2) Работа совершается при любом перемещении тела. 3) Работа силы трения скольжения всегда отрицательна. 4) Работа силы упругости по замкнутому контуру не равна нулю. 5) Работа силы трения не зависит от формы траектории.

Часть 2

13. Лебёдка равномерно поднимает груз массой 300 кг на высоту 3 м за 10 с. Какова мощность лебёдки?

Лекция: Работа.Мощность.КПД

Лекция. Тема:

Работа. Мощность. КПД.

1.Изучаем теоретический материал. (записываем основные определения и формулы)

Работа А

– скалярная физическая величина, измеряемая произведением модуля силы, действующей на тело, на модуль его перемещения под действием этой силы и на косинус угла между векторами силы и перемещения:

Здесь:

модуль перемещения тела, под действием силы ,

работа, которую совершила сила

На графиках в осях F-S

(рис.1) работа силы численно равна площади фигуры, ограниченной графиком, осью перемещения и прямыми, параллельными оси силы.

Если на тело действует несколько сил, то в формуле работы F

– это не равнодействующая ma всех этих сил, а именно та сила, которая и совершает работу. Если локомотив тянет вагоны, то этой силой является сила тяги локомотива, если на канате поднимают тело, то этой силой является сила натяжения каната. Это может быть и сила тяжести и сила трения, если в условии задачи речь идет о работе именно этих сил.

Мощность

Для характеристики работоспособности и быстроты соверше­ния работы введено понятие мощности.

Мощность — работа, выполненная в единицу времени:

Единицы измерения мощности: ватты, киловатты,

Мощность при поступательном движении

(рис. 16.1)

где F

— модуль силы, действующей на тело;
vcp
— средняя скорость движения тела.

Средняя мощность при поступательном движении равна про­изведению модуля силы на среднюю скорость перемещения и на ко­синус угла между направлениями силы и скорости.

Мощность при вращении

(рис. 16.2) Тело движется по дуге радиуса

Р = Мвр

ω
ср
где ω
ср
— средняя угловая скорость.

Мощность силы при вращении равна произведению вращающе­го момента на среднюю угловую скорость.

Если при выполнении работы усилие машины и скорость дви­жения меняются, можно определить мощность в любой момент вре­мени, зная значения усилия и скорости в данный момент.

Коэффициент полезного действия

Каждая машина и механизм, совершая работу, тратит часть энергии на преодоление вредных сопротивлений.

Таким образом, машина (механизм) кроме полезной работы совершает еще и дополнительную работу.

Отношение полезной работы к полной работе или полезной мощности ко всей затраченной мощности называется коэффициентом по­лезного действия (КПД):

Полезная работа (мощность) расходуется на движение с заданной скоростью и определяется по формулам:

Затраченная мощность больше полезной на величину мощности, идущей на преодоление трения в звеньях машины, на утечки и тому подобные потери.

Чем выше КПД, тем совершеннее машина.

2. Разбираем примеры решения задач. (даны задачи)

Пример 1.

Определение работы.

Тело мас­сой 2 кг под дей­стви­ем силы F

пе­ре­ме­ща­ет­ся вверх по на­клон­ной плос­ко­сти на рас­сто­я­ние Рас­сто­я­ние тела от по­верх­но­сти Земли при этом уве­ли­чи­ва­ет­ся на .

Век­тор силы F

на­прав­лен па­рал­лель­но на­клон­ной плос­ко­сти, мо­дуль силы
F
равен 30 Н. Какую ра­бо­ту при этом пе­ре­ме­ще­нии в си­сте­ме от­сче­та, свя­зан­ной с на­клон­ной плос­ко­стью, со­вер­ши­ла сила
F
? Уско­ре­ние сво­бод­но­го па­де­ния при­ми­те рав­ным , ко­эф­фи­ци­ент тре­ния

Решение: Ра­бо­та силы опре­де­ля­ет­ся как ска­ляр­ное про­из­ве­де­ние век­то­ра силы и век­то­ра пе­ре­ме­ще­ния тела. Сле­до­ва­тель­но, сила F

при подъ­еме тела вверх по на­клон­ной плос­ко­сти со­вер­ши­ла ра­бо­ту.

Ответ:

Пример 2. Определение мощности.

Определить потребную мощность мотора лебедки для подъема груза весом 3 кН на высоту 10 м за 2,5 с (рис. 16.3). КПД механизма лебедки 0,75.

Решение

1. Мощность мотора используется на подъем груза с заданной скоростью и преодоление вредных сопротивлений механизма лебедки.

Полезная мощность определяется по формуле Р

= F
v
cosα. В данном случае α = 0; груз движется поступательно.

S 10

2. Скорость подъема груза v =

—;
v =
— = 4 м/с.

T 2,5

3. Необходимое усилие равно весу груза (равно­мерный подъем).

4. Полезная мощность Р =

3000 ∙ 4 = 12 000 Вт.

5. Полная мощность, затрачиваемая мотором,

Пример 3. Определение КПД.

Судно движется со скоростью 56 км/ч (рис. 16.4). Двигатель развивает мощность 1200 кВт. Определить силу сопротивления воды движению судна. КПД машины 0,4.

Решение

1. Определяем полезную мощность, используемую на движение с заданной скоростью:

2. По формуле для полезной мощности можно определить движу­щую силу судна с учетом условия α =

0. При равномерном движении движущая сила равна силе сопротивления воды:
F дв = Fconp .
Сила сопротивления воды движению судна Fсопр = 48 кН.

Пример 5.

Точильный камень прижимается к обрабатываемой детали с силой 1,5 кН (рис. 16.5). Какая мощность затрачивается на обработку де­тали, если коэффициент трения материа­ла камня о деталь 0,28; деталь вращается со скоростью 100 об/мин, диаметр детали 60 мм.

Решение

1. Резание осуществляется за счет трения между точильным камнем и обра­батываемой деталью:

3. Угловая скорость вращения детали

4. Мощность, необходимая для обработки детали:

3.Закрепление материала. Пройти тесты по теме. ссылка
https://multiurok.ru/tests/35174/
4. Домашнее задание. (с помощью теоретического материала и примера решения задач решить предложенные задачи самостоятельно).

Вопрос 1.

Подвесной лодочный мотор развивает мощность 22000 Вт. Какую работу (МДж) может совершить мотор при перевозке груза за 30 минут?

Вопрос 2.

Какую мощность (кВт) развивает подъемный кран, равномерно поднимая груз массой 2,5 т на высоту 15 м за 2,5 мин?

Вопрос 3.

Механическая лопата, приводимая в движение электродвигателем мощностью 3,68 кВт, поднимает 180 т песка на высоту 6 м в течение 1 ч. Каков КПД установки?

Вопрос 4.

Сколько времени (ч) должен работать насос мощностью 50 кВт, чтобы из шахты глубиной 150 м откачать воду объемом 200 м3?

Вопрос 5.

Двигатель насоса, развивая некоторую мощность, поднимает 200 м3 воды на высоту 10 м за 5 мин. КПД двигателя 40 %. Найдите мощность (кВт) двигателя.

Вопрос 6.

Трактор на пахоте преодолевает силу сопротивления 10 кН, развивая мощность 36 кВт. С какой скоростью движется трактор?

Вопрос 7.

Электровоз при движении со скоростью 54 км/ч потребляет мощность 600 кВт. Определите силу тяги (кН) электровоза, если его КПД равен 75%.

Коэффициент полезного действия

КПД — это отношение полезной работы, совершенной машиной, ко всей затраченной работе (подведенной энергии) за то же время

Коэффициент полезного действия выражается в процентах. Чем ближе это число к 100%, тем выше производительность машины. Не может быть КПД больше 100, так как невозможно выполнить больше работы, затратив меньше энергии.

КПД наклонной плоскости — это отношение работы силы тяжести, к затраченной работе по перемещению вдоль наклонной плоскости.