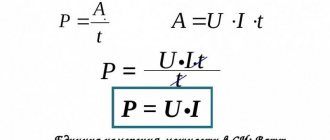Content
If a force acts on a body and it moves, then mechanical work is done. We know that this physical quantity depends on the applied force and the distance traveled ($A = Fs$) and is measured in joules.
Obviously, it takes different amounts of time to complete the same work in different cases. For example, you need to raise a cabinet to the ninth floor of a house. If it is loaded into an elevator, the work will be completed in a few seconds. What if the loader lifts the cabinet on foot up the stairs? This type of work will take much longer to complete.
In the same way, a truck can move a certain amount of cargo in one go, whereas a passenger car will have to travel several times to its destination and back to deliver the entire load.
Thus, a new physical quantity appears that allows us to describe how quickly this or that work can be done.
Definition and formula of work
Definition
In the event that, under the influence of a force, a change in the modulus of the speed of movement of a body occurs, then they say that the force does work
.
It is believed that if the speed increases, then the work is positive, if the speed decreases, then the work done by the force is negative. The change in the kinetic energy of a material point during its movement between two positions is equal to the work done by the force: $$A=\Delta E_{k}=\frac{m v_{2}^{2}}{2}-\frac{ m v_{1}^{2}}{2}(1)$$
The action of a force on a material point can be characterized not only by changing the speed of movement of the body, but by the amount of displacement that the body in question makes under the influence of the force ($\ bar{F}$).
Power determination
The speed of work is characterized by a physical quantity called power.
Power is a physical quantity equal to the ratio of work to the time during which it was performed.
To calculate power, you need to divide the work by the time during which this work was done:
$$power = \frac{work}{time}$$
or
$$N = \frac{A}{t}$$
where $N$ is power, $A$ is work, $t$ is the time it takes to complete the work.
Power can be:
- Constant if the same work is done every second
- Non-constant if different work is done every second. In this case, we talk about average power: $N_{avg} = \frac{A}{t}$
Elementary work
The elementary work $(\delta A)$ of some force $\bar{F}$ is defined as the scalar product:
$$\delta A=\bar{F} \cdot d \bar{r}=F \cdot ds \cdot \cos \alpha(2)$$
$\bar{r}$ radius is the vector of the point to which the force is applied, $\bar{r}$ is the elementary displacement of the point along the trajectory, $\alpha$ is the angle between the vectors $ds=|d \bar{r}| $ and $d\bar{r}$. If $\alpha$ is an obtuse angle, the work is less than zero, if the angle $\alpha$ is acute, then the work is positive, for $\alpha=\frac{\pi}{2} \delta A=0$
In Cartesian coordinates, formula (2) has the form:
$$\delta A=F_{x} d x+F_{y} d y+F_{z} dz(3)$$
where Fx,Fy,Fz are projections of the vector $\bar{F}$ onto the Cartesian axes.
When considering the work of a force applied to a material point, you can use the formula:
$$\delta A=\bar{F} \bar{v} dt=\bar{v} d \bar{p}(4)$$
where $\bar{v}$ is the velocity of the material point, $\bar{p}$ is the momentum of the material point.
If several forces act on a body (mechanical system) simultaneously, then the elementary work that these forces do on the system is equal to:
$$\delta A=\sum_{i=1}^{n} \delta A_{i}=\sum_{i=1}^{n} \bar{F}_{i} d \bar{r} _{i}=\sum_{i=1}^{n} \bar{F}_{i} \bar{v}_{i} dt(5)$$
where the summation of the elementary work of all forces is carried out, dt is a small period of time during which the elementary work $\delta$ is performed on the system.
The resulting work of internal forces, even if the rigid body is moving, is zero.
Let a rigid body rotate around a fixed point - the origin (or a fixed axis that passes through this point). In this case, the elementary work of all external forces (let’s assume that their number is n) that act on the body is equal to:
$$\delta A=\bar{M} \bar{\omega} dt=\bar{M} d \bar{\varphi}(6)$$
where $\bar{M}$ is the resulting moment of forces relative to the rotation point, $d \bar{\varphi}$ is the vector of elementary rotation, $\bar{w}$ is the instantaneous angular velocity.
Power unit
A unit of power is taken to be the power at which 1 J of work is done in 1 s.
This unit is called the watt (W) in honor of the scientist Watt (Figure 1).
Figure 1. James Watt (1736-1819) - Scottish engineer and inventor.
From the power formula $N = \frac{A}{t}$:
$$1 \space watt = \frac{1 \space joule}{1 \space second} = 1 \frac{J}{s}$$
Other power units often used are kilowatt (kW), megawatt (MW) and milliwatt (mW):
$1 \space MW = 1,000,000 \space W$
$1 \space W = 0.000001 MW$
$1 \space kW = 1000 \space W$
$1 \space W = 0.001 kW$
$1 \space mW = 0.001 \space W$
$1 \space W = 1000 \space mW$
Power is also sometimes measured in horsepower (hp):
$1 \space l. With. = 735.5 \space W$
$1 \space W = 0.00013596 \space hp$
This unit of measurement is not as popular as the watt, but is still used, for example, in the automotive industry.
EXAMPLES OF TASKS
Part 1
1. The work is determined by the formula
1) \( A=Fv \) 2) \( A=N/t \) 3) \( A=mv \) 4) \( A=FS \)
2. The load is evenly lifted vertically upward by a rope tied to it. The work of gravity in this case
1) equal to zero 2) positive 3) negative 4) more than the work of the elastic force
3. The box is pulled by a rope tied to it, making an angle of 60° with the horizontal, applying a force of 30 N. What is the work done by this force if the modulus of displacement is 10 m?
1) 300 J 2) 150 J 3) 3 J 4) 1.5 J
4. An artificial Earth satellite, whose mass is equal to \( m \), moves uniformly in a circular orbit with radius \( R \). The work done by gravity in a time equal to the period of revolution is equal to
1) \( mgR \) 2) \( \pi mgR \) 3) \( 2\pi mgR \) 4) \( 0 \)
5. A car weighing 1.2 tons travels 800 m along a horizontal road. How much work was done by the friction force if the friction coefficient is 0.1?
1) -960 kJ 2) -96 kJ 3) 960 kJ 4) 96 kJ
6. A spring with a stiffness of 200 N/m is stretched by 5 cm. How much work will the elastic force do when the spring returns to equilibrium?
1) 0.25 J 2) 5 J 3) 250 J 4) 500 J
7. Balls of the same mass roll down a slide along three different chutes, as shown in the figure. In which case will the work done by gravity be greatest?
1) 1 2) 2 3) 3 4) the work is the same in all cases
8. Work along a closed path is zero
A. Frictional forces B. Elastic forces
The correct answer is
1) both A and B 2) only A 3) only B 4) neither A nor B
9. The SI unit of power is
1) J 2) W 3) J s 4) N m
10. What is the useful work if the work done is 1000 J and the engine efficiency is 40%?
1) 40000 J 2) 1000 J 3) 400 J 4) 25 J
11. Establish a correspondence between the work of force (in the left column of the table) and the sign of work (in the right column of the table). In your answer, write down the selected numbers under the corresponding letters.
WORK OF FORCE A. Work of elasticity when stretching a spring B. Work of friction B. Work of gravity when a body falls
SIGN OF WORK 1) positive 2) negative 3) equal to zero
12. From the statements below, choose two correct ones and write their numbers in the table.
1) The work of gravity does not depend on the shape of the trajectory. 2) Work is done during any movement of the body. 3) The work done by the sliding friction force is always negative. 4) The work done by the elastic force along a closed contour is not zero. 5) The work of the friction force does not depend on the shape of the trajectory.
Part 2
13. A winch uniformly lifts a load weighing 300 kg to a height of 3 m in 10 s. What is the power of the winch?
Lecture: Work. Power. Efficiency
Lecture. Subject:
Job. Power. Efficiency
1. We study theoretical material. (we write down the basic definitions and formulas)
Job A
– a scalar physical quantity measured by the product of the modulus of the force acting on the body, the modulus of its displacement under the influence of this force and the cosine of the angle between the vectors of force and displacement:
Here:
module of body movement, under the influence of force,
work done by the force
On graphs in FS
(Fig. 1) the work of force is numerically equal to the area of the figure limited by the graph, the axis of displacement and straight lines parallel to the axis of force.
If several forces act on a body, then in the work formula F
- this is not the resultant ma of all these forces, but precisely the force that does the work. If a locomotive pulls cars, then this force is the traction force of the locomotive; if a body is lifted on a rope, then this force is the tension force of the rope. This can be both the force of gravity and the force of friction, if the problem statement deals with the work of these particular forces.
Power
To characterize the performance and speed of work, the concept of power was introduced.
Power is work done per unit of time:
Power units: watts, kilowatts,
Forward power
(Fig. 16.1)
where F
— modulus of force acting on the body;
v cp
is the average speed of the body.
The average power during translational motion is equal to the product of the modulus of force by the average speed of movement and by the cosine of the angle between the directions of force and speed.
Rotating power
(Fig. 16.2) The body moves along an arc of radius
P = M time
ω
ср
where ω
ср
is the average angular velocity.
The power of the force during rotation is equal to the product of the torque and the average angular velocity.
If, while performing work, the force of the machine and the speed of movement change, you can determine the power at any time, knowing the values of force and speed at a given moment.
Efficiency
Each machine and mechanism, when doing work, spends part of its energy to overcome harmful resistances.
Thus, the machine (mechanism), in addition to useful work, also performs additional work.
The ratio of useful work to total work or useful power to all expended power is called efficiency factor (efficiency):
Useful work (power) is spent on movement at a given speed and is determined by the formulas:
The expended power is greater than the useful power by the amount of power used to overcome friction in machine links, leaks and similar losses.
The higher the efficiency, the more perfect the machine.
2. We analyze examples of problem solving. (tasks given)
Example 1.
Definition of work.
A body of mass 2 kg under the action of force F
moves up an inclined plane at a distance. The distance of the body from the Earth's surface increases by .
Force vector F
is directed parallel to the inclined plane, the modulus of the force
F
F
during this movement in the reference frame associated with the inclined plane ? Take the free fall acceleration equal to , friction coefficient
Solution: The work of a force is defined as the scalar product of the force vector and the displacement vector of the body. Therefore, the force F
performed work when lifting a body up an inclined plane.
Answer:
Example 2. Determination of power.
Determine the required winch motor power to lift a load weighing 3 kN to a height of 10 m in 2.5 s (Fig. 16.3). The efficiency of the winch mechanism is 0.75.
Solution
1. The motor power is used to lift the load at a given speed and overcome the harmful resistance of the winch mechanism.
Useful power is determined by the formula P
= F
v
cosα. In this case α = 0; the load moves forward.
S 10
2. Load lifting speed v =
—;
v =
— = 4 m/s.
T 2.5
3. The required force is equal to the weight of the load (uniform lifting).
4. Useful power P =
3000 ∙ 4 = 12,000 W.
5. The total power expended by the motor is
Example 3. Determination of efficiency.
The ship is moving at a speed of 56 km/h (Fig. 16.4). The engine develops a power of 1200 kW. Determine the force of water resistance to the movement of the vessel. Machine efficiency is 0.4.
Solution
1. Determine the useful power used to move at a given speed:
2. Using the formula for useful power, you can determine the driving force of the vessel, taking into account the condition α =
0. With uniform motion, the driving force is equal to the resistance force of the water:
F dv = F conp .
The force of water resistance to the movement of the vessel Fresist = 48 kN.
Example 5.
The whetstone is pressed against the workpiece with a force of 1.5 kN (Fig. 16.5). How much power is spent on processing the part if the coefficient of friction of the stone material on the part is 0.28; the part rotates at a speed of 100 rpm, the diameter of the part is 60 mm.
Solution
1. Cutting is carried out due to friction between the grindstone and the workpiece:
3. Angular speed of rotation of the part
4. Power required to process the part:
3.Secure the material.
Take tests on the topic. link https://multiurok.ru/tests/35174/
4. Homework. (with the help of theoretical material and an example of problem solving, solve the proposed problems yourself).
Question 1.
The outboard motor develops a power of 22,000 watts. How much work (MJ) can the motor do when transporting a load in 30 minutes?
Question 2.
What power (kW) does a crane develop when uniformly lifting a load weighing 2.5 tons to a height of 15 m in 2.5 minutes?
Question 3.
A mechanical shovel driven by a 3.68 kW electric motor lifts 180 tons of sand to a height of 6 m within 1 hour. What is the efficiency of the installation?
Question 4.
How long (hours) should a 50 kW pump run to pump out 200 m3 of water from a 150 m deep mine?
Question 5.
The pump motor, developing some power, lifts 200 m3 of water to a height of 10 m in 5 minutes. Engine efficiency is 40%. Find the power (kW) of the motor.
Question 6.
When plowing, the tractor overcomes a resistance force of 10 kN, developing a power of 36 kW. At what speed is the tractor moving?
Question 7.
When moving at a speed of 54 km/h, an electric locomotive consumes 600 kW of power. Determine the traction force (kN) of an electric locomotive if its efficiency is 75%.
Efficiency
Efficiency is the ratio of the useful work done by a machine to all the work expended (energy supplied) during the same time
The efficiency is expressed as a percentage. The closer this number is to 100%, the higher the machine's performance. There cannot be an efficiency greater than 100, since it is impossible to do more work using less energy.
The efficiency of an inclined plane is the ratio of the work done by gravity to the work expended in moving along the inclined plane.