Всем доброго времени суток. В прошлой статье я рассказал о магнитном поле и немного остановился на его параметрах. Данная статья продолжает тему магнитного поля и посвящена такому параметру как магнитная индукция. Для упрощения темы я буду рассказывать о магнитном поле в вакууме, так как различные вещества имеют разные магнитные свойства, и как следствие необходимо учитывать их свойства.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Закон Био – Савара – Лапласа
В результате исследования магнитных полей создаваемых электрическим током, исследователи пришли к таким выводам:
- магнитная индукция, создаваемая электрическим током пропорциональна силе тока;
- магнитная индукция имеет зависимость от формы и размеров проводника, по которому протекает электрический ток;
- магнитная индукция в любой точке магнитного поля зависит от расположения данной точки по отношению к проводнику с током.
Французские учёные Био и Савар, которые пришли к таким выводам обратились к великому математику П. Лапласу для обобщения и вывода основного закона магнитной индукции. Он высказал гипотезу, что индукция в любой точке магнитного поля, создаваемое проводником с током можно представить в виде суммы магнитных индукций элементарных магнитных полей, которые создаются элементарным участком проводника с током. Данная гипотеза и стала законом магнитной индукции, называемого законом Био – Савара – Лапласа. Для рассмотрения данного закона изобразим проводник с током и создаваемую им магнитную индукцию
Магнитная индукция dB, создаваемая элементарным участком проводника dl.
Тогда магнитная индукция dB элементарного магнитного поля, которое создается участком проводника dl, с током I в произвольной точке Р будет определяться следующим выражением
где I – сила тока, протекающая по проводнику,
r – радиус-вектор, проведённый от элемента проводника к точке магнитного поля,
dl – минимальный элемент проводника, который создает индукцию dB,
k – коэффициент пропорциональности, зависящий от системы отсчёта, в СИ k = μ0/(4π)
Так как является векторным произведением, тогда итоговое выражение для элементарной магнитной индукции будет выглядеть следующим образом
Таким образом, данное выражение позволяет найти магнитную индукцию магнитного поля, которое создается проводником с током произвольной формы и размеров при помощи интегрирования правой части выражения
где символ l обозначает, что интегрирование происходит по всей длине проводника.
Магнитное поле прямого тока в проводе, имеющем конечную длину
Допустим, что у нас имеется прямой тонкий провод, конечной длины по которому течет неизменяющийся ток $I$ (рис.2). Определим, какова магнитная индукция поля в точке $C$, создаваемая этим проводом.
Рисунок 2. Магнитное поле прямого тока в проводе, имеющем конечную длину. Автор24 — интернет-биржа студенческих работ
Полярные углы, соответствующие концам проводника будем считать равными $\varphi_{1}=a$ и $\varphi_{2}=b$.
Вектор магнитной индукции перпендикулярен плоскости рисунка. Силовые линии – это окружности, как и у бесконечного проводника.
Модуль элементарного магнитного поля ($dB$), которое создает малый участок $dl$ (рис.2) по закону Био-Савара-Лапласа запишем так:
$dB=\frac{\mu_{0}}{4\pi }\frac{Idl\sin \alpha }{r^{2}}=\frac{\mu_{0}I}{4\pi R}\cos {\varphi d\varphi }\left( 12 \right)$
где из рис.2 видно, что:
- $\sin {\alpha =\cos {\varphi ;}\, }$
- $dl\cos {\varphi =rd\varphi ;\, }$
- $r=\frac{R}{\cos \varphi }.$
Воспользуемся принципом суперпозиции и получим магнитное поле в точке $C$, создаваемое всеми участками проводника с током:
$B=\int\limits_a^b {\frac{\mu_{0}I}{4\pi R}\cos {\varphi d\varphi }=}\frac{\mu_{0}I}{4\pi R}\left( \sin \left( b \right)-\sin \left( a \right)\right)\left( 13 \right)$
Если рассматривать бесконечно длинный проводник, как частный случай прямого проводника с током, то следует учесть, что для него:
$a=-\frac{\pi }{2};\, b=\frac{\pi }{2}$,
тогда из (13) следует:
$B=\frac{\mu_{0}I}{2\pi R}\left( 14 \right)$
Результат (14) снова совпал с (7) и (11).
Магнитная индукция прямолинейного проводника
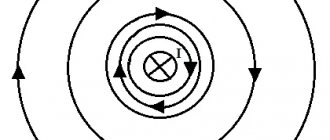
Как известно простейшее магнитное поле создает прямолинейный проводник, по которому протекает электрический ток. Как я уже говорил в предыдущей статье, силовые линии данного магнитного поля представляют собой концентрические окружности расположенные вокруг проводника.
Магнитная индукция магнитного поля создаваемого прямолинейным проводником с током.
Для определения магнитной индукции В прямого провода в точке Р введем некоторые обозначения. Так как точка Р находится на расстоянии b от провода, то расстояние от любой точки провода до точки Р определяется как r = b/sinα. Тогда наименьшую длину проводника dl можно вычислить из следующего выражения
В итоге закон Био – Савара – Лапласа для прямолинейного провода бесконечной длины будет иметь вид
где I – ток, протекающий по проводу,
b – расстояние от центра провода до точки, в которой рассчитывается магнитная индукция.
Теперь просто проинтегрируем получившееся выражение по dα в пределах от 0 до π.
Таким образом, итоговое выражение для магнитной индукции прямолинейного провода бесконечной длины будет иметь вид
где μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м,
I – ток, протекающий по проводу,
b – расстояние от центра проводника до точки, в которой измеряется индукция.
Действие магнитного поля на проводник с током (закон Ампера) и на движущийся заряд (сила Лоренца)
Закон Ампера. На элемент проводника с током I , помещённый в магнитное поле с индукцией (рис. 12), действует сила (– сила Ампера):
.
Модуль вектора : ,
где – угол между векторами и .
Направление вектора можно определить по правилу левой руки: если силовые линии входят в ладонь, а четыре вытянутых пальца располагаются по току, то отведённый большой палец укажет направление вектора силы Ампера .
(Сила перпендикулярна плоскости рисунка 12.)
Сила Лоренца. На заряд q , движущийся со скоростью в магнитном поле с индукцией (рис. 13), действует сила ( – сила Лоренца ):
.
Модуль вектора : ,
где α – угол между векторами и .
Направление вектора может быть определено по правилу левой руки для движущихся положительных зарядов и по правилу правой руки для движущихся отрицательных зарядов:
если силовые линии магнитного поля входят в ладонь, а четыре вытянутых пальца располагаются по скорости движения частицы, то отведённый большой палец укажет направление силы Лоренца (рис. 13, сила перпендикулярна плоскости рисунка).
Магнитная индукция кольца
Индукция прямого провода имеет небольшое значение и уменьшается при удалении от проводника, поэтому в практических устройствах практически не применяется. Наиболее широко используются магнитные поля созданные проводом, намотанным на какой либо каркас. Поэтому такие поля называются магнитными полями кругового тока. Простейшим таким магнитным поле обладает электрический ток, протекающий по проводнику, который имеет форму окружности радиуса R.
В данном случае практический интерес представляет два случая: магнитное поле в центре окружности и магнитное поле в точке Р, которое лежит на оси окружности. Рассмотрим первый случай.
Магнитная индукция в центре кругового тока.
В данном случае каждый элемент тока dl создаёт в центре окружности элементарную магнитную индукцию dB, которая перпендикулярна к плоскости контура, тогда закон Био-Савара-Лапласа будет иметь вид
Остается только проинтегрировать полученное выражение по всей длине окружности
где μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м,
I – сила тока в проводнике,
R – радиус окружности, в которое свернут проводник.
Рассмотрим второй случай, когда точка, в которой вычисляется магнитная индукция, лежит на прямой х, которая перпендикулярна плоскости ограниченной круговым током.
Магнитная индукция в точке, лежащей на оси окружности.
В данном случае индукция в точке Р будет представлять собой сумму элементарных индукций dBX, которые в свою очередь представляет собой проекцию на ось х элементарной индукции dB
Применив закон Био-Савара-Лапласа вычислим величину магнитной индукции
Теперь проинтегрируем данное выражение по всей длине окружности
где μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м,
I – сила тока в проводнике,
R – радиус окружности, в которое свернут проводник,
х – расстояние от точки, в которой вычисляется магнитная индукция, до центра окружности.
Как видно из формулы при х = 0, получившееся выражение переходит в формулу для магнитной индукции в центре кругового тока.
Магнитное поле кругового тока в его центре
Рисунок 1. Магнитное поле кругового тока в его центре. Автор24 — интернет-биржа студенческих работ
Рассмотрим круговой проводник, по которому течет постоянный ток $I$ (рис.1). Выделим на этом проводнике элемент $dl$, который можно считать прямолинейным. Если перейти к другому элементу этого же тока, затем к третьему и так далее, применить правило правого винта, то очевидно, что все магнитные поля, созданные этими элементами в центре, направлены вдоль одной прямой, перпендикуляру к плоскости кольца. Это означает, применяя принцип суперпозиции, мы векторное сложение заменим алгебраическим.
Запишем закон Био-Савара-Лапласа для модуля вектора индукции поля, создаваемого элементом d$l_1$:
$dB=\frac{\mu_{0}\mu }{4\pi }\frac{Idl_{1}\sin \alpha }{r^{2}}\left( 5\right).$
Из рис.1 мы видим:
- что расстояние от элементарного тока до центра витка равно его радиусу ($R$) и будет одинаковым для всех элементов на этом витке,
- элемент $dl$ (как и все остальные элементы) будут нормальны к радиус-вектору $\vec r$.
Учитывая сказанное выражение (5) представим в виде:
$dB=\frac{\mu_{0}\mu }{4\pi }\frac{Idl_{1}}{R^{2}}\left( 6 \right)$.
Обезличивая витки с током, положим далее $dl_1=dl$.
Поскольку наш ток является непрерывным, то для нахождения полного поля в его центре, мы проинтегрируем (6), имеем:
$B=\oint\limits_L {dB=} \frac{\mu_{0}\mu }{4\pi}\frac{I}{R^{2}}\oint\limits_L {dl} =\frac{\mu_{0}\mu }{4\pi}\frac{I}{R^{2}}2\pi R\to$
$B=\mu_{0}\mu \frac{I}{2R}\left( 7 \right)$.
Замечание 1
$L=2πR$ — длина окружности витка.
Индукция магнитного поля кругового тока на его оси
Найдем индукцию магнитного поля на оси кругового тока, если ток, текущий по нему равен $I$, радиус витка — $R$ (рис.2).
Рисунок 2. Индукция магнитного поля кругового тока на его оси. Автор24 — интернет-биржа студенческих работ
Как основу для выполнения поставленной задачи возьмем закон Био-Савара-Лапласа (1), где из рис.2 мы видим, что:
- $\vec{r}=\vec{R}+\vec{h}$,
- $d\vec{l}\times \vec{r}=d\vec{l}\times \vec{R}+d\vec{l}\times \vec{h}(9).$
Используя принцип суперпозиции закон (1) для нашего тока и формулы (8-9) запишем:
$\vec{B}=\oint\limits_L {dB=}$$\frac{\mu \mu_{0}}{4\pi }I\oint\limits_L \frac{d\vec{l}\times\vec{r}}{r^{3}} $ $=\frac{\mu \mu_{0}}{4\pi }\frac{I}{r^{3}}\left( \oint\limits_L{d\vec{l}\times \vec{R}+} \oint\limits_L {d\vec{l}\times \vec{h}}\right)\left( 10 \right).$
В выражении (10) при записи интеграла, мы учли, что величина вектора $\vec{r}$ не изменяется. Кроме этого вектор $\vec h$, определяющий положение точки, в которой мы ищем поле, не изменяется при движении по нашему контуру, поэтому:
$\oint\limits_L {d\vec{l}\times \vec{h}} =(\oint\limits_L {d\vec{l})\times\vec{h}} =0\, \left( 11 \right),$
так как ( $\oint\limits_L {d\vec{l})=0.}$
Вычислим интеграл: $\oint\limits_L {d\vec{l}\times \vec{R}.}$ Введем единичный вектор ($\vec n$), нормальный к плоскости витка с током.
$\oint\limits_L {d\vec{l}\times \vec{R}=\oint\limits_L {\vec{n}Rdl=\vec{n}R}} \oint\limits_L {dl=\vec{n}R} 2\pi R=2\pi R^{2}\vec{n}\left( 12 \right)$.
Подставляем результаты интегрирования из (12) в (10), имеем:
$\vec{B}=\frac{\mu \mu_{0}}{4\pi }\frac{I}{r^{3}}2\pi R^{2}\vec{n}=\frac{\mu\mu_{0}I}{2}\frac{R^{2}}{\left( R^{2}+h^{2}\right)^{\frac{3}{2}}}\vec{n}\left( 13 \right)$
где при записи окончательного результата мы учли, что:
$r^{3}=\left( R^{2}+h^{2} \right)^{\frac{3}{2}}$.
Циркуляция вектора магнитной индукции
Для расчёта магнитной индукции простых магнитных полей достаточно закона Био-Савара-Лапласа. Однако при более сложных магнитных полях, например, магнитное поле соленоида или тороида, количество расчётов и громоздкость формул значительно увеличится. Для упрощения расчётов вводится понятие циркуляции вектора магнитной индукции.
Циркуляция вектора магнитной индукции по произвольному контуру.
Представим некоторый контур l, который перпендикулярный току I. В любой точке Р данного контура, магнитная индукция В направлена по касательной к данному контуру. Тогда произведение векторов dl и В описывается следующим выражением
Так как угол dφ достаточно мал, то векторов dlВ определяется, как длина дуги
Таким образом, зная магнитную индукцию прямолинейного проводника в данной точке, можно вывести выражение для циркуляции вектора магнитной индукции
Теперь остаётся проинтегрировать получившееся выражение по всей длине контура
В нашем случае вектор магнитной индукции циркулирует вокруг одного тока, в случае же нескольких токов выражение циркуляции магнитной индукции переходит в закон полного тока, который гласит:
Циркуляция вектора магнитной индукции по замкнутому контуру пропорциональна алгебраической сумме токов, которые охватывает данный контур.
Магнитный поток. Теорема Гаусса для магнитного поля
Поток вектора магнитной индукции (или магнитный поток) через произвольную площадку S характеризуется числом силовых линий магнитного поля, пронизывающих данную площадку S.
Если площадка S расположенаперпендикулярно силовым линиям магнитного поля (рис. 14), то поток ФB вектора индукции через данную площадку S :
.
Рис. 14 Рис. 15
Если площадка S расположена неперпендикулярно силовым линиям магнитного поля (рис. 15), то поток ФB вектора индукции через данную площадку S :
,
где α – угол между векторами и нормали к площадке S.
,Для того, чтобы найти поток ФB вектора магнитной индукции через произвольную поверхность S, необходиморазбить эту поверхность на элементарные площадки dS (рис. 16)иопределить элементарный поток вектора через каждую площадку dS по формуле:
где α – угол между векторами и нормали к данной площадке dS;
Тогда поток вектора через произвольную поверхность S равен алгебраической сумме элементарных потоков через все элементарные площадки dS, на которые разбита поверхность S, что приводит к интегрированию:
– вектор, равный по величине площади площадки dS и направленный по вектору нормали к данной площадке dS .
.
Теорема Гаусса для магнитного поля
Для произвольной замкнутой поверхности S (рис. 17) поток вектора индукции магнитного поля через эту поверхность S можно рассчитать по формуле:
.
С другой стороны, число линий магнитной индукции, входящих внутрь объема, ограниченного этой замкнутой поверхностью, равно числу линий, выходящих из этого объема (рис. 17). Поэтому, с учетом того, что поток вектора индукции магнитного поля считается положительным, если силовые линии выходят из поверхности S, и отрицательным для линий, входящих в поверхность S, суммарный поток ФB вектора через произвольную замкнутую поверхность S равен нулю, т.е.:
,
что составляет формулировку теоремы Гаусса для магнитного поля.
Явление электромагнитной индукции. Закон Фарадея
Явление возникновения электрического тока в замкнутом проводящем контуре в результате изменения магнитного потока, пронизывающего этот контур, называется явлением электромагнитной индукции. Возникновение индукционного электрического тока в контуре указывает на наличие в этом контуре электродвижущей силы, называемой электродвижущей силой (ЭДС) электромагнитной индукции.
Согласно закону Фарадея величина ЭДС электромагнитной индукции определяется только скоростью изменения магнитного потока, пронизывающего проводящий контур, а именно:
величина ЭДС электромагнитной индукции прямо пропорциональна скорости изменения магнитного потока, пронизывающего проводящий контур:
(закон Фарадея).
Направление индукционного тока в контуре определяется по правилу Ленца: индукционный ток в контуре всегда имеет такое направление, что создаваемое этим током магнитное поле препятствует изменению магнитного потока, вызвавшему этот индукционный ток.
Закон Фарадея с учетом правила Ленца можно сформулировать следующим образом: величина ЭДС электромагнитной индукции в контуре численно равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную этим контуром, то есть:
(закон Фарадея с учетом правила Ленца).
Для нахождения индукции магнитного поля в центре кругового проводника с током необходимо разбить этот проводник на элементы , для каждого из них найти вектор , а затем все эти векторы сложить. Так как все векторы направлены вдоль нормали к плоскости витка (рис. 11), то сложение векторов можно заменить сложением их модулей dB.
По закону Био-Савара-Лапласа модуль вектора :
.
Так как все элементы проводника перпендикулярны соответствующим радиусам-векторам , то sina = 1 для всех элементов . Расстояния r = R для всех элементов проводника . Тогда выражение для модуля вектора :
.
Теперь можно перейти к интегрированию:
.
Итак, индукция магнитного поля в центре кругового проводника с током:
(R – радиус витка с током I).
Действие магнитного поля на проводник с током (закон Ампера) и на движущийся заряд (сила Лоренца)
Закон Ампера. На элемент проводника с током I , помещённый в магнитное поле с индукцией (рис. 12), действует сила (– сила Ампера):
.
Модуль вектора : ,
где – угол между векторами и .
Направление вектора можно определить по правилу левой руки: если силовые линии входят в ладонь, а четыре вытянутых пальца располагаются по току, то отведённый большой палец укажет направление вектора силы Ампера .
(Сила перпендикулярна плоскости рисунка 12.)
Сила Лоренца. На заряд q , движущийся со скоростью в магнитном поле с индукцией (рис. 13), действует сила ( – сила Лоренца ):
.
Модуль вектора : ,
где α – угол между векторами и .
Направление вектора может быть определено по правилу левой руки для движущихся положительных зарядов и по правилу правой руки для движущихся отрицательных зарядов:
если силовые линии магнитного поля входят в ладонь, а четыре вытянутых пальца располагаются по скорости движения частицы, то отведённый большой палец укажет направление силы Лоренца (рис. 13, сила перпендикулярна плоскости рисунка).