Для использования в других целях см. Соленоид (значения).
| Эта статья поднимает множество проблем. Пожалуйста помоги | эта статья может быть слишком техническим для большинства читателей, чтобы понять . Пожалуйста помогите улучшить это к Сделайте это понятным для неспециалистов, не снимая технических деталей. |
| эта статья нужны дополнительные цитаты для проверка . Пожалуйста помоги улучшить эту статью к добавление цитат в надежные источники. Материал, не полученный от источника, может быть оспорен и удален. |
(Узнайте, как и когда удалить этот шаблон сообщения)
Иллюстрация соленоида Магнитное поле создается семиконтурным соленоидом (вид в разрезе), описанным с использованием полевые линии
А соленоид
(/ˈsoʊлəпɔɪd/,[1] от Греческий σωληνοειδής
sōlēnoeidḗs
, «трубчатая»[2]) является разновидностью электромагнит, целью которого является создание контролируемого магнитное поле через катушку, намотанную в плотно упакованный спираль. Катушка может быть расположена для создания однородного магнитного поля в объеме пространства, когда электрический ток проходит через него. Период, термин
соленоид
был придуман в 1823 г. Андре-Мари Ампер для обозначения спиральной катушки.[3]
При изучении электромагнетизм, соленоид — это катушка, длина которой существенно больше ее диаметра.[4] Спиральная катушка соленоида не обязательно должна вращаться вокруг прямой оси; Например, Уильям СтердженЭлектромагнит 1824 года состоял из соленоида, изогнутого в форме подковы.
В инженерное дело, термин может также относиться к множеству преобразователь устройства, которые конвертируют энергия в линейное движение.[5] Проще говоря, соленоид преобразует электроэнергия в механическая работа. Этот термин также часто используется для обозначения соленоидный клапан, интегрированное устройство, содержащее электромеханический соленоид, который приводит в действие либо пневматический или гидравлический клапан или соленоидный переключатель, который является определенным типом реле который внутри использует электромеханический соленоид для управления электрический выключатель; например, соленоид стартера автомобиля или линейный соленоид. Болты соленоида, Тип электромеханического блокирующего механизма, также существует. В электромагнитной технологии соленоид — это привод узел со скользящим ферромагнитным поршнем внутри катушки. Без питания плунжер выходит на часть своей длины за пределы катушки; подача энергии втягивает поршень в катушку. Электромагниты с неподвижными сердечниками не считаются соленоидами.
Содержание
- 1 Бесконечный непрерывный соленоид 1.1 Внутри
- 1.2 за пределами
- 1.3 Количественное описание
- 6.1 Электромеханический соленоид 6.1.1 Пропорциональный соленоид
Бесконечный непрерывный соленоид
Бесконечный соленоид имеет бесконечную длину, но конечный диаметр. «Непрерывный» означает, что соленоид образован не дискретными катушками конечной ширины, а множеством бесконечно тонких катушек без промежутков между ними; в этой абстракции соленоид часто рассматривается как цилиндрический лист проводящего материала.
Внутри
Рисунок 1: Бесконечный соленоид с тремя произвольными Петли ампер маркированный а
,
б
, и
c
. Интегрирование по пути
c
показывает, что магнитное поле внутри соленоида должно быть радиально однородным.
В магнитное поле внутри бесконечно длинного соленоида однороден, и его прочность не зависит ни от расстояния от оси, ни от площади поперечного сечения соленоида.
Это вывод плотность магнитного потока вокруг соленоида, который достаточно длинный, чтобы можно было игнорировать краевые эффекты. На рисунке 1 мы сразу знаем, что вектор плотности потока направлен в положительную z
направление внутри соленоида, а в отрицательном
z
направление вне соленоида. Мы подтверждаем это, применяя правило захвата правой рукой для поля вокруг проволоки. Если мы обхватим правой рукой провод, указав большим пальцем в направлении тока, изгиб пальцев покажет, как ведет себя поле. Поскольку мы имеем дело с длинным соленоидом, все компоненты магнитного поля, не направленные вверх, компенсируются симметрией. Снаружи происходит аналогичная отмена, а поле только направлено вниз.
Теперь рассмотрим воображаемую петлю c
который расположен внутри соленоида. К Закон Ампера, мы знаем, что линейный интеграл из
B
(вектор плотности магнитного потока) вокруг этого контура равен нулю, так как он не содержит электрических токов (можно также предположить, что контур электрическое поле прохождение через контур является постоянным при таких условиях: постоянный или постоянно меняющийся ток через соленоид). Выше мы показали, что поле направлено вверх внутри соленоида, поэтому горизонтальные участки контура
c
ничего не вносят в интеграл. Таким образом, интеграл от верхней части 1 равен интегралу обратной стороны 2. Поскольку мы можем произвольно изменять размеры контура и получить тот же результат, единственное физическое объяснение состоит в том, что подынтегральные выражения фактически равны, то есть магнитное поле внутри соленоида радиально однородно. Однако обратите внимание, что ничто не запрещает ему изменяться в продольном направлении, что на самом деле так и есть.
за пределами
Аналогичный аргумент можно применить к циклу а
чтобы сделать вывод, что поле вне соленоида радиально однородно или постоянно. Этот последний результат, который строго выполняется только около центра соленоида, где силовые линии параллельны его длине, важен, поскольку он показывает, что плотность потока снаружи практически равна нулю, поскольку радиусы поля вне соленоида будут стремиться к бесконечность.
Также можно использовать интуитивный аргумент, чтобы показать, что плотность потока вне соленоида фактически равна нулю. Линии магнитного поля существуют только в виде петель, они не могут расходиться или сходиться к точке, как силовые линии электрического поля (см. Закон Гаусса для магнетизма). Линии магнитного поля следуют продольной траектории соленоида внутри, поэтому они должны идти в противоположном направлении за пределами соленоида, чтобы линии могли образовывать петлю. Однако объем снаружи соленоида намного больше, чем объем внутри, поэтому плотность силовых линий снаружи значительно снижается. Напомним, что внешнее поле постоянно. Чтобы общее количество силовых линий было сохранено, внешнее поле должно стремиться к нулю по мере увеличения длины соленоида.
Конечно, если соленоид выполнен в виде проволочной спирали (как это часто делается на практике), то он излучает внешнее поле так же, как одиночный провод, из-за тока, протекающего по всей длине соленоида.
Количественное описание
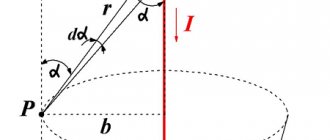
На картинке показано, как Закон Ампера может применяться к соленоиду
Применение Обходной закон Ампера к соленоиду (см. рисунок справа) дает нам
B л = μ 0 N я , { displaystyle Bl = mu _ {0} NI,}
где B { displaystyle B} это плотность магнитного потока, л { displaystyle l} длина соленоида, μ 0 { displaystyle mu _ {0}} это магнитная постоянная, N { displaystyle N} количество витков, и я { displaystyle I} электрический ток. Отсюда получаем
B = μ 0 N я л . { displaystyle B = mu _ {0} { frac {NI} {l}}.}
Это уравнение справедливо для соленоида в свободном пространстве, что означает, что проницаемость магнитного пути такая же, как проницаемость свободного пространства, μ0.
Если соленоид погружен в материал с относительной проницаемостью μр, то поле увеличивается на эту величину:
B = μ 0 μ р N я л . { displaystyle B = mu _ {0} mu _ { mathrm {r}} { frac {NI} {l}}.}
В большинстве соленоидов соленоид не погружен в материал с более высокой проницаемостью, а скорее некоторая часть пространства вокруг соленоида имеет материал с более высокой проницаемостью, а часть — просто воздух (который ведет себя как свободное пространство). В этом сценарии полный эффект материала с высокой проницаемостью не виден, но будет эффективная (или кажущаяся) проницаемость. μ
эфф такое, что 1 ≤
μ
эфф ≤
μ
р.
Включение ферромагнитный ядро, например утюг, увеличивает величину плотности магнитного потока в соленоиде и увеличивает эффективную проницаемость магнитного пути. Это выражается формулой
B = μ 0 μ е ж ж N я л = μ N я л , { displaystyle B = mu _ {0} mu _ { mathrm {eff}} { frac {NI} {l}} = mu { frac {NI} {l}},}
где μ
эфф эффективная или кажущаяся проницаемость керна. Эффективная проницаемость является функцией геометрических свойств керна и его относительной проницаемости. Термины относительная проницаемость (свойство только материала) и эффективная проницаемость (свойство всей конструкции) часто путают; они могут различаться на много порядков.
Для открытой магнитной структуры соотношение между эффективной проницаемостью и относительной проницаемостью определяется следующим образом:
μ е ж ж = μ р 1 + k ( μ р − 1 ) , { displaystyle mu _ { mathrm {eff}} = { frac { mu _ {r}} {1 + k ( mu _ {r} -1)}},}
где k
— коэффициент размагничивания сердечника.[6]
Магнитное поле, создаваемое катушкой
Когда электрический ток проходит через обмотки катушек, он ведет себя как электромагнит, и плунжер, который находится внутри катушки, притягивается к центру катушки с помощью магнитного потока внутри корпуса катушек, который, в свою очередь, сжимает небольшая пружина прикреплена к одному концу плунжера. Сила и скорость движения плунжеров определяются силой магнитного потока, генерируемого внутри катушки.
Когда ток питания выключен (обесточен), электромагнитное поле, созданное ранее катушкой, разрушается, и энергия, накопленная в сжатой пружине, заставляет поршень вернуться в исходное положение покоя. Это движение плунжера вперед и назад известно как «ход» соленоидов, другими словами, максимальное расстояние, на которое плунжер может проходить в направлении «вход» или «выход», например, 0–30 мм.
Такой тип соленоида обычно называется линейным соленоидом из-за линейного направленного движения и действия плунжера. Линейные соленоиды доступны в двух основных конфигурациях, которые называются «тягового типа», так как он тянет подключенную нагрузку к себе, когда они находятся под напряжением, и «толкающего типа», которые действуют в противоположном направлении, отталкивая его от себя при подаче питания. Как притягивающие, так и толкающие типы обычно имеют одинаковую конструкцию, с разницей в расположении возвратной пружины и конструкции плунжера.
Магнитное поле, создаваемое внутри.
Конечный непрерывный соленоид
Магнитное поле линия и плотность, создаваемые соленоидом с поверхностью плотность тока
Конечный соленоид — это соленоид конечной длины. Непрерывный означает, что соленоид образован не отдельными катушками, а листом проводящего материала. Мы предполагаем, что ток равномерно распределен по поверхности соленоида, при этом поверхность плотность тока K
; в цилиндрические координаты:
K → = я л ϕ ^ . { displaystyle { vec {K}} = { frac {I} {l}} { hat { phi}}.}
Магнитное поле можно найти с помощью векторный потенциал, что для конечного соленоида радиуса р
и длина
л
в цилиндрических координатах ( ρ , ϕ , z ) { displaystyle ( rho, phi, z)} является[7]
А ϕ = μ 0 я 4 π 1 л р ρ [ ζ k ( k 2 + час 2 − час 2 k 2 час 2 k 2 K ( k 2 ) − 1 k 2 E ( k 2 ) + час 2 − 1 час 2 Π ( час 2 , k 2 ) ) ] ζ − ζ + , { displaystyle A _ { phi} = { frac { mu _ {0} I} {4 pi}} { frac {1} {l}} { sqrt { frac {R} { rho} }} left [ zeta k left ({ frac {k ^ {2} + h ^ {2} -h ^ {2} k ^ {2}} {h ^ {2} k ^ {2}}) } K (k ^ {2}) — { frac {1} {k ^ {2}}} E (k ^ {2}) + { frac {h ^ {2} -1} {h ^ {2 }}} Pi (h ^ {2}, k ^ {2}) right) right] _ { zeta _ {-}} ^ { zeta _ {+}},}
где
ζ ± = z ± л 2 , { displaystyle zeta _ { pm} = z pm { frac {l} {2}},} час 2 = 4 р ρ ( р + ρ ) 2 , { displaystyle h ^ {2} = { frac {4R rho} {(R + rho) ^ {2}}},} k 2 = 4 р ρ ( р + ρ ) 2 + ζ 2 , { Displaystyle к ^ {2} = { гидроразрыва {4R rho} {(R + rho) ^ {2} + zeta ^ {2}}},} K ( м ) = ∫ 0 π / 2 1 1 − м грех 2 θ d θ , { Displaystyle К (м) = int _ {0} ^ { pi / 2} { frac {1} { sqrt {1-m sin ^ {2} theta}}} d theta,} E ( м ) = ∫ 0 π / 2 1 − м грех 2 θ d θ , { displaystyle E (m) = int _ {0} ^ { pi / 2} { sqrt {1-m sin ^ {2} theta}} d theta,} Π ( п , м ) = ∫ 0 π / 2 1 ( 1 − п грех 2 θ ) 1 − м грех 2 θ d θ . { displaystyle Pi (n, m) = int _ {0} ^ { pi / 2} { frac {1} {(1-n sin ^ {2} theta) { sqrt {1- m sin ^ {2} theta}}}} d theta.}
Вот, K ( м ) { Displaystyle К (м)} , E ( м ) { Displaystyle E (м)} , и Π ( п , м ) { Displaystyle Pi (п, м)} полны эллиптические интегралы первого, второго и третьего рода.
С помощью
B → = ∇ × А → , { displaystyle { vec {B}} = nabla times { vec {A}},}
плотность магнитного потока получается как[8][9][10]
B ρ = μ 0 я 4 π 2 л р ρ [ k 2 − 2 k K ( k 2 ) + 2 k E ( k 2 ) ] ζ − ζ + , { displaystyle B _ { rho} = { frac { mu _ {0} I} {4 pi}} { frac {2} {l}} { sqrt { frac {R} { rho} }} left [{ frac {k ^ {2} -2} {k}} K (k ^ {2}) + { frac {2} {k}} E (k ^ {2}) right ] _ { zeta _ {-}} ^ { zeta _ {+}},} B z = μ 0 я 4 π 1 л 1 р ρ [ ζ k ( K ( k 2 ) + р − ρ р + ρ Π ( час 2 , k 2 ) ) ] ζ − ζ + . { displaystyle B_ {z} = { frac { mu _ {0} I} {4 pi}} { frac {1} {l}} { frac {1} { sqrt {R rho} }} left [ zeta k left (K (k ^ {2}) + { frac {R- rho} {R + rho}} Pi (h ^ {2}, k ^ {2}) right) right] _ { zeta _ {-}} ^ { zeta _ {+}}.}
На оси симметрии радиальная составляющая обращается в нуль, а осевая составляющая поля равна
B z = μ 0 N я 2 ( л / 2 − z л р 2 + ( л / 2 − z ) 2 + л / 2 + z л р 2 + ( л / 2 + z ) 2 ) { displaystyle B_ {z} = { frac { mu _ {0} NI} {2}} { Biggl (} { frac {l / 2-z} {l { sqrt {R ^ {2}) + (l / 2-z) ^ {2}}}}} + { frac {l / 2 + z} {l { sqrt {R ^ {2} + (l / 2 + z) ^ {2}) }}}} { Biggr)}} .
Внутри соленоида, вдали от концов ( | z | ≪ л / 2 − р { displaystyle | z | ll l / 2-R} ), это стремится к постоянному значению B = μ 0 N я / л { displaystyle B = mu _ {0} NI / l} .
Рабочий цикл соленоида
Другим более практичным способом уменьшения тепла, выделяемого катушкой соленоидов, является использование «прерывистого рабочего цикла». Прерывистый рабочий цикл означает, что катушка многократно переключается «ВКЛ» и «ВЫКЛ» на подходящей частоте, чтобы активировать механизм плунжера, но не дать ему обесточиться во время периода ВЫКЛ. Прерывистое переключение рабочего цикла является очень эффективным способом уменьшения общей мощности, потребляемой катушкой.
Рабочий цикл (% ED) соленоида — это часть времени «ВКЛ», когда на электромагнит подается напряжение, и это отношение времени «ВКЛ» к общему времени «ВКЛ» и «ВЫКЛ» для одного полного цикла операций. Другими словами, время цикла равно времени включения плюс время выключения. Рабочий цикл выражается в процентах, например:
Будет интересно➡ Что такое катушка индуктивности и почему ее иногда называют дроссель
Затем, если соленоид включен или включен на 30 секунд, а затем выключен на 90 секунд перед повторным включением, один полный цикл, общее время цикла включения / выключения составит 120 секунд, (30 + 90) поэтому рабочий цикл соленоидов будет рассчитываться как 30/120 сек или 25%. Это означает, что вы можете определить максимальное время включения соленоидов, если вам известны значения рабочего цикла и времени выключения.
Например, время выключения равно 15 секундам, рабочий цикл равен 40%, поэтому время включения равно 10 секундам. Соленоид с номинальным рабочим циклом 100% означает, что он имеет постоянное номинальное напряжение и поэтому может быть оставлен включенным или постоянно включен без перегрева или повреждения. В этом уроке о соленоидах мы рассматривали как линейный соленоид, так и вращающийся соленоид как электромеханический привод, который можно использовать в качестве выходного устройства для управления физическим процессом. В следующем уроке мы продолжим рассмотрение устройств вывода, называемых исполнительными механизмами, и устройства, которое снова преобразует электрический сигнал в соответствующее вращательное движение, используя электромагнетизм. Тип устройства вывода, которое мы рассмотрим в следующем уроке — это двигатель постоянного тока.
Материал по теме: Что такое реле времени.
Соленоид в упаковке
Оценка конечного прерывистого соленоида
В случае, когда радиус намного больше длины соленоида, плотность магнитного потока через центр соленоида (в z
направление, параллельное длине соленоида, где катушка центрируется в
z
= 0) можно оценить как магнитную индукцию одиночной круглой проводящей петли:
B z = μ 0 я N р 2 2 ( р 2 + z 2 ) 3 2 { displaystyle B_ {z} = { frac { mu _ {0} INR ^ {2}} {2 (R ^ {2} + z ^ {2}) ^ { frac {3} {2}} }}}
Для случаев, когда радиус невелик по сравнению с длиной, эту оценку можно дополнительно уточнить, суммируя ее по N
количество витков / витков проволоки в разных положениях вдоль
z
.
Примеры нестандартных соленоидов (а) разреженный соленоид, (б) соленоид с переменным шагом, (в) нецилиндрический соленоид
Соленоиды косвенного действия
Данный вид соленоида является более сложным, и понадобится больше времени для объяснения механизма его работы. Проще говоря, соленоид косвенного действия состоит из двух клапанов, соединённых в один механизм. Основной клапан (main valve) – это золотник, который работает по описанному выше принципу, второй используемый механизм – это управляющий клапан (pilot valve), который находится между золотником и электромагнитом. Управляющий клапан представляет собой маленький соленоид прямого действия, который активирует нажатие большого золотника. Обратите внимание, что соленоид, показанный на данном изображении, является соленоидом прямого действия, так как он напрямую воздействует на управляющий клапан, но вся конструкция в сборе является соленоидом косвенного действия.
Основное различие между соленоидами прямого действия и косвенного действия в том, как они взаимодействуют с механическими частями маркера. Соленоиды прямого действия работают напрямую с элементами механизма маркера. Соленоиды косвенного действия используют воздушный поток для управления золотником. Основная причина существования соленоидов косвенного действия – это их невероятно низкое потребление энергии по сравнению с соленоидами прямого действия. Например, если соленоиду прямого действия необходимо 4 ватта для воздействия на механизм, то соленоиду косвенного действия для того же воздействия нужно всего 0,5 ватта.
Схема работы соленоида.
Далее соленоиды делятся по количеству потоков. Для функционирования у соленоида должно быть хотя бы одно отверстие, через которое воздух поступает в соленоид, одно отверстие, из которого воздух поступает в механизм, и одно отверстие для сброса воздуха. Но в большинстве случаев используется конструкция с двумя отверстиями для подачи воздуха в механизм маркера и двумя отверстиями сброса воздуха. В настоящее время, в основном, используются три основных типа соленоидов:
- Четырёхпоточный золотниковый клапан (four way spool valve). Этот тип используется в большинстве полностью электропневматических маркеров, где для движения поршня назад и вперёд используется воздух. Например Ego, Angel, Shocker, Dye Matrix и т.п. Неправильно названный тривей (three way valve) на кокерах, тоже является примером четырёхпоточного поршня.
- Трехпоточный золотник, закрытый в состоянии покоя (3-way spool normally closed). Это трехпоточный клапан, который подаёт воздух при подаче на него напряжения. Когда этот соленоид в состоянии покоя, он не подаёт никакого давления, например pVI Shocker, Invert Mini.
- Трёхпоточный золотник, открытый в состоянии покоя (3-way spool normally open). Это трёхпоточный клапан, который подаёт давление в состоянии покоя, и перекрывает поток воздуха, когда на него подаётся напряжение, например Ion.
Управляющий клапан в соленоиде всегда является трёхпоточным, закрытым в состоянии покоя. Когда на соленоид подаётся напряжение, управляющий клапан открывается и подаёт воздух для того, чтобы сдвинуть золотник, который, в свою очередь, может быть и трехпоточным и четырёхпоточным.
Каждый соленоид косвенного действия делится на три сегмента: катушка (coil), управляющий клапан (pilot) и золотник (spool). Катушка – это единственная электромагнитная часть всего механизма. Состоит она из медной проволоки, обмотанной вокруг металлического кожуха, внутри которого находится металлический стержень, являющийся противоположным магнитным компонентом клапана. Стержень изготавливается из стали и имеет пружину с одного конца. На противоположном конце соленоида находится золотник, который является клапаном и основной движущейся частью соленоида. Золотники обычно изготавливаются из латуни или алюминия в зависимости от производителя.
Будет интересно➡ Что такое датчик Холла
Также на золотнике имеются разнообразные прокладки для того, чтобы перенаправлять воздушные потоки. И, наконец, последняя часть соленоида – управляющий клапан, который является “посредником” между движением стержня катушки и золотника. Основной компонент для управляющего клапана – круглый поршень, который передвигает золотник в открытое положение. Поршень представляет собой маленький пластиковый диск с прокладкой вокруг него. За поршнем находится маленький привод, деталь для удержания привода на месте и маленькая заглушка, находящаяся внутри привода. Большинство этих компонентов, как и корпус управляющего клапана, изготавливается из полимеров для того, чтобы улучшить скольжение и уплотнение.
Интересный материал для ознакомления: что такое вариасторы.
В заключение статьи, что же такое двелл? Это время, в течение которого на соленоид подаётся напряжение (соответственно, путь болта маркера в переднее положение + время, которое болт находится в переднем положении, выпуская воздух). При сильном понижении параметра двелл вам придётся компенсировать более короткое время пребывания болта в переднем положении путём повышения рабочего давления маркера, что не будет полезным для вашего маркера. Слишком завышенное значение параметра двелл приведёт к перерасходу воздуха, заряда батареи и большему износу самого соленоида.
Два одинаковых соленоида.
Неправильные соленоиды
В категории конечных соленоидов есть те, которые редко намотаны с одним шагом, редко намотаны с переменным шагом (соленоиды с переменным шагом) или с переменным радиусом для разных петель (нецилиндрические соленоиды). Их называют нерегулярными соленоидами. Они нашли применение в различных областях, таких как соленоиды с редкой намоткой для беспроводной передачи энергии,[11][12] соленоиды переменного шага для магнитно-резонансной томографии (МРТ),[13] и нецилиндрические соленоиды для других медицинских устройств.[14]
Расчет собственной индуктивности и емкости не может быть выполнен с использованием тех, которые используются для традиционных соленоидов, то есть с плотно намотанными соленоидами. Предложены новые методы расчета собственной индуктивности.[15](коды доступны на [16]) и емкости.[17] (коды доступны на [18])
Вращательный соленоид
Большинство электромагнитных соленоидов являются линейными устройствами, создающими линейную силу движения или движения вперед и назад. Однако имеются также вращательные соленоиды, которые производят угловое или вращательное движение из нейтрального положения либо по часовой стрелке, против часовой стрелки, либо в обоих направлениях (в двух направлениях). Вращающиеся соленоиды можно использовать для замены небольших двигателей постоянного тока или шаговых двигателей, если угловое движение очень мало, а угол поворота — это угол, смещенный от начального к конечному положению.
Будет интересно➡ Что такое импульсное реле
Обычно доступные ротационные соленоиды имеют перемещения 25, 35, 45, 60 и 90 o, а также многократные перемещения к определенному углу и от него, такие как самовосстановление в двух положениях или возврат в нулевое вращение, например, от 0 до 90- до -0 ° , самовосстановление в 3 положениях, например от 0 ° до +45 ° или от 0 ° до -45 °, а также фиксация в 2 положениях.
Соленоид в металлическом корпусе.
Вращающиеся соленоиды производят вращательное движение, когда под напряжением, обесточено, или изменение полярности электромагнитного поля изменяет положение ротора с постоянными магнитами. Их конструкция состоит из электрической катушки, намотанной вокруг стальной рамы с магнитным диском, соединенным с выходным валом, расположенным над катушкой.
Когда катушка находится под напряжением, электромагнитное поле генерирует множество северных и южных полюсов, которые отталкивают соседние постоянные магнитные полюса диска, заставляя его вращаться на угол, определяемый механической конструкцией вращающегося соленоида.
Вращающиеся соленоиды используются в торговых автоматах или игровых автоматах, для управления клапанами, затворами камер со специальными высокоскоростными, низкоэнергетическими или регулируемыми позиционирующими соленоидами с высоким усилием или крутящим моментом, такими как те, которые используются в точечно-матричных принтерах, пишущих машинках, автоматах или в автомобилях.
Схема устройства соленоида.
Индуктивность
Смотрите также: Индуктивность с физической симметрией
Как показано выше, плотность магнитного потока B { displaystyle B} внутри катушки практически постоянна и определяется выражением
B = μ 0 N я л , { displaystyle B = mu _ {0} { frac {NI} {l}},}
где μ
0 это магнитная постоянная, N { displaystyle N} количество витков, я { displaystyle I} текущий и л { displaystyle l} длина катушки. Игнорируя конечные эффекты, общее магнитный поток через катушку получается путем умножения плотности потока B { displaystyle B} по площади поперечного сечения А { displaystyle A} :
Φ = μ 0 N я А л . { displaystyle Phi = mu _ {0} { frac {NIA} {l}}.}
Объединяя это с определением индуктивность
L = N Φ я , { displaystyle L = { frac {N Phi} {I}},}
индуктивность соленоида равна
L = μ 0 N 2 А л . { displaystyle L = mu _ {0} { frac {N ^ {2} A} {l}}.}
Таблица индуктивности для коротких соленоидов с различным соотношением диаметра к длине была рассчитана Деллингером, Уиттмором и Ульдом.[19]
Это, а также индуктивность более сложных форм, можно получить из Уравнения Максвелла. Для жестких катушек с воздушным сердечником индуктивность зависит от геометрии катушки и количества витков и не зависит от тока.
Аналогичный анализ применим к соленоиду с магнитным сердечником, но только если длина катушки намного больше, чем произведение относительного проницаемость магнитопровода и диаметра. Это ограничивает простой анализ сердечниками с низкой проницаемостью или очень длинными тонкими соленоидами. Наличие сердечника можно учесть в приведенных выше уравнениях, заменив магнитную постоянную μ0
с
μ
или
μ0μр
, где
μ
представляет проницаемость и
μр
относительная проницаемость. Обратите внимание, что поскольку проницаемость ферромагнитный материалы изменяются в зависимости от приложенного магнитного потока, индуктивность катушки с ферромагнитным сердечником обычно изменяется в зависимости от тока.
Снижение энергопотребления соленоида
Одним из основных недостатков соленоидов, особенно линейного соленоида, является то, что они являются «индуктивными устройствами», изготовленными из катушек с проволокой. Это означает, что соленоидная катушка преобразует часть электрической энергии, используемой для их работы, в «нагрев» из-за сопротивления провода. Другими словами, при длительном подключении к источнику электропитания они нагреваются, и чем дольше время, в течение которого питание подается на соленоидную катушку, тем горячее становится. Также, когда катушка нагревается, ее электрическое сопротивление также изменяется, позволяя течь большему току, повышая ее температуру.
При постоянном входном напряжении, подаваемом на катушку, катушка соленоидов не имеет возможности остыть, потому что входная мощность всегда включена. Чтобы уменьшить этот самогенерируемый эффект нагрева, необходимо уменьшить либо количество времени, в течение которого катушка находится под напряжением, либо уменьшить количество тока, протекающего через нее. Один из способов потребления меньшего тока заключается в подаче подходящего достаточно высокого напряжения на электромагнитную катушку, чтобы обеспечить необходимое электромагнитное поле для работы и посадки плунжера, но затем один раз активировать для снижения напряжения питания катушек до уровня, достаточного для поддержания плунжера, в «сидячем» или закрытом положении.
Используя этот метод, соленоид может быть подключен к его источнику напряжения на неопределенный срок (непрерывный рабочий цикл), так как мощность, потребляемая катушкой, и выделяемое тепло значительно уменьшаются, что может быть до 85-90% при использовании подходящего силового резистора. Однако мощность, потребляемая резистором, также будет генерировать определенное количество тепла, I 2 R (закон Ома), и это также необходимо учитывать.
Приложения
Электромеханический соленоид
Объяснение 1920 года коммерческого соленоида, используемого в качестве электромеханического привода.
Электромеханические соленоиды состоят из электромагнитно индуктивный катушка, намотанная на подвижную стали или утюг слизняк (названный арматура). Катушка имеет такую форму, что якорь можно перемещать в пространство в центре катушки и из него, изменяя индуктивность катушки и тем самым становясь электромагнит. Движение якоря используется для придания механической силы некоторому механизму, например, для управления пневматический клапан. Хотя соленоиды обычно слабы на любых расстояниях, кроме очень коротких, они могут управляться напрямую схемой контроллера, и поэтому они имеют очень быстрое время реакции.
Сила, приложенная к якорю, пропорциональна изменению индуктивности катушки относительно изменения положения якоря и тока, протекающего через катушку (см. Закон индукции Фарадея). Сила, приложенная к якорю, всегда будет перемещать якорь в направлении, увеличивающем индуктивность катушки.
Электромеханические соленоиды обычно встречаются в электронных маркеры для пейнтбола, автоматы для игры в пинбол, матричные принтеры, и топливные форсунки. Некоторые жилые дверные звонки использовать электромеханические соленоиды, при этом электризация катушки заставляет якорь ударять о металлические перегородки.[20]Электромеханический, или рабочий соленоид, возможно, впервые был изобретен в Англии Иллитисом Августом Тиммисом. В 1893 году ему был выдан патент US506282 на соленоид, имеющий стержень из железа и внешнюю оболочку для эффективного распространения магнитного потока, как это делается сегодня.
Пропорциональный соленоид
К этой категории соленоидов относятся магнитные цепи уникальной конструкции, которые влияют на аналоговое позиционирование плунжера или якоря соленоида в зависимости от тока катушки. Эти соленоиды, осевые или вращающиеся, используют геометрию, несущую магнитный поток, которая одновременно создает высокую пусковую силу (крутящий момент) и имеет участок, который быстро начинает насыщаться магнитным путем. Результирующий профиль силы (крутящего момента) по мере того, как соленоид продвигается через свой рабочий ход, почти плоский или снижается от высокого до более низкого значения. Соленоид может быть полезен для позиционирования, остановки в середине хода или для срабатывания при низкой скорости; особенно в системе управления с обратной связью. Однонаправленный соленоид будет срабатывать против противодействующей силы, или двойная соленоидная система будет самоцикличной. Пропорциональная концепция более подробно описана в публикации SAE 860759 (1986).
Фокусировка магнитного поля и сопутствующее ему измерение потока, как показано в документе SAE, требуется для создания высокого пускового усилия в начале хода соленоида и для поддержания уровня или уменьшения силы по мере того, как соленоид перемещается через свой диапазон смещения. Это совершенно противоположно тому, что происходит с обычными соленоидами с уменьшающимся воздушным зазором. Фокусировка магнитного поля к рабочему воздушному зазору первоначально создает высокий mmf (ампер-витки) и относительно низкий уровень магнитного потока через воздушный зазор. Этот высокий продукт потока mmf x (считываемая энергия) создает высокую пусковую силу. При увеличении плунжера (ds) энергия движения F ∙ ds извлекается из энергии воздушного зазора. Из-за приращения движения плунжера незначительно увеличивается проницаемость воздушного зазора, увеличивается магнитный поток, незначительно уменьшается mmf в воздушном зазоре; все это приводит к поддержанию высокого продукта потока mmf x. Из-за повышенного уровня магнитного потока рост падений ампер-витков в других частях железной цепи (преимущественно в геометрии полюсов) вызывает уменьшение ампер-витков воздушного зазора и, следовательно, снижение потенциальной энергии поля в воздушном зазоре. Дальнейшее увеличение плунжера вызывает постоянное уменьшение силы соленоида, тем самым создавая идеальные условия для управления движением, которое контролируется током, подаваемым на катушку соленоида. Вышеупомянутая геометрия полюса с линейно изменяющейся площадью траектории приводит к почти линейному изменению силы. Противодействующее усилие пружины или двухсторонний соленоид (две катушки) позволяет контролировать движение вперед и назад. Управление с обратной связью улучшает линейность и жесткость системы.
Поворотный соленоид
Поворотный соленоид — это электромеханическое устройство, используемое для вращения трещотка механизм при подаче питания. Они использовались в 1950-х годах для автоматизации поворотного переключателя в электромеханических элементах управления. При повторном нажатии поворотного соленоида мгновенный переключатель перемещается вперед на одно положение. Два поворотные приводы на противоположных концах вала поворотного кнопочного переключателя, может перемещать или реверсировать положение переключателя.
Поворотный соленоид похож на линейный соленоид, за исключением того, что сердечник якоря установлен в центре большого плоского диска, с тремя наклонными дорожками качения, вписанными в нижнюю часть диска. Эти канавки совпадают с дорожками качения на корпусе соленоида, разделенными шарикоподшипниками в дорожках качения.
Когда соленоид активирован, сердечник якоря магнитно притягивается к полюсу статора, и диск вращается на шарикоподшипниках в дорожках качения по мере продвижения к корпусу катушки. При отключении питания пружина на диске возвращает его в исходное положение как во вращении, так и в осевом направлении.
Вращающийся соленоид был изобретен в 1944 году Джорджем Х. Леландом из Дейтона, штат Огайо, чтобы обеспечить более надежный и устойчивый к ударам / вибрации механизм сброса бомб, сбрасываемых с воздуха. Ранее использовавшиеся линейные (осевые) соленоиды были подвержены непреднамеренному срабатыванию. В патенте США № 2496880 описываются электромагнит и наклонные дорожки качения, которые составляют основу изобретения. Инженер Леланда, Эрл В. Керман, сыграл важную роль в разработке совместимой скобы сброса бомбы, которая включала в себя вращающийся соленоид. Кандалы этого типа обнаружены в фюзеляже самолета B-29, выставленном в Национальном музее ВВС США в Дейтоне, штат Огайо. Соленоиды этого разнообразия продолжают использоваться в бесчисленных современных приложениях и до сих пор производятся под оригинальным брендом Leland «Ledex», который теперь принадлежит Джонсон Электрик.
Появившийся на рынке в 1980-х годах, исключительно вращающийся соленоид со сбалансированным 3-лопастным ротором с железными лопастями предлагал улучшенную виброизоляцию за счет исключения осевого движения ротор. Это устройство обеспечивает пропорциональное бесшумное позиционирование, а также быстрое вращение для сортировки почты и ворот конвейера. Затем последовала версия ротора с постоянными магнитами (патент США 5,337,030; 1994), которая обеспечивала быстрое электрическое двунаправленное вращение.
Роторная звуковая катушка
Роторный звуковая катушка представляет собой вращающуюся версию соленоида. Обычно неподвижный магнит находится снаружи, а часть катушки движется по дуге, управляемой током, протекающим через катушки. Вращающиеся звуковые катушки широко используются в таких устройствах, как Дисковый привод.[нужна цитата
] Рабочая часть измеритель с подвижной катушкой также представляет собой тип вращающейся звуковой катушки, которая вращается вокруг оси указателя, волосковая пружина обычно используется для обеспечения слабой почти линейной восстанавливающей силы.
Пневматический электромагнитный клапан
Соленоид пневмоклапана
Пневматический соленоидный клапан это переключатель для направления воздуха на любой пневматический устройство, обычно привод, позволяя относительно небольшому сигналу управлять большим устройством. Это также интерфейс между электронными контроллерами и пневматическими системами.[нужна цитата
]
Гидравлический электромагнитный клапан
Гидравлические электромагнитные клапаны в целом аналогичны пневматическим соленоидным клапанам, за исключением того, что они регулируют поток гидравлическая жидкость (нефть), часто при давлении около 3000 фунтов на квадратный дюйм (210 бар, 21 МПа, 21 МН / м²). Гидравлическое оборудование использует соленоиды для управления потоком масла к гидроцилиндрам или исполнительным механизмам. Клапаны с электромагнитным управлением часто используются в ирригационных системах, где относительно слабый соленоид открывает и закрывает небольшой пилотный клапан, который, в свою очередь, активирует главный клапан за счет приложения давления жидкости к поршню или диафрагме, которые механически соединены с основным клапаном. также присутствуют в предметах повседневного обихода, таких как стиральные машины, для регулирования потока и количества воды в барабане.
Соленоиды трансмиссии регулируют поток жидкости через автоматическую коробку передач и обычно устанавливаются в корпусе клапана трансмиссии.
Соленоид автомобильного стартера
Основная статья: Соленоид стартера
В легковом или грузовом автомобиле соленоид стартера является частью автомобиль система зажигания двигателя. Соленоид стартера получает большой электрический ток от автомобильный аккумулятор и небольшой электрический ток от выключатель зажигания. Когда ключ зажигания включен (то есть когда ключ повернут для запуска автомобиля), небольшой электрический ток вынуждает соленоид стартера замкнуть пару тяжелых контактов, тем самым передавая большой электрический ток на пусковой двигатель. Это разновидность реле.
Соленоиды стартера также могут быть встроены в сам стартер, часто видимые снаружи стартера. Если соленоид стартера получает недостаточную мощность от аккумулятора, он не сможет запустить мотор и может издавать быстрый характерный «щелкающий» или «щелкающий» звук. Это может быть вызвано низким или полностью разряженным аккумулятором, ржавый или неплотное соединение с аккумулятором, или сломанный или поврежденный положительный (красный) кабель от аккумулятора. Любое из них приведет к подаче на соленоид некоторой мощности, но недостаточной для удержания тяжелых контактов в замкнутом состоянии, поэтому сам стартер никогда не вращается, и двигатель не запускается.
Описание и принцип работы соленоида
Линейный соленоид работает на том же основном принципе, что и электромеханическое реле, описанное в предыдущем уроке, и точно так же, как и реле, они также могут переключаться и управляться с помощью транзисторов или полевых МОП-транзисторов. Линейный соленоид — это электромагнитное устройство, которое преобразует электрическую энергию в механическое толкающее или тянущее усилие или движение. Линейный соленоид в основном состоит из электрической катушки, намотанной вокруг цилиндрической трубки с ферромагнитным приводом или «плунжером», который может свободно перемещать или скользить «ВХОД» и «ВЫХОД» в корпусе катушек. Виды соленоидов представлены на рисунке ниже.
Соленоиды могут использоваться для электрического открывания дверей и защелок, открытия или закрытия клапанов, перемещения и управления роботизированными конечностями и механизмами и даже для включения электрических выключателей только путем подачи питания на его катушку. Соленоиды доступны в различных форматах, причем наиболее распространенными типами являются линейный соленоид, также известный как линейный электромеханический привод (LEMA) и вращающийся соленоид.
Соленоид и сфера применения
Оба типа соленоидов, линейный и вращательный доступны в виде удержания (с постоянным напряжением) или в виде защелки (импульс ВКЛ-ВЫКЛ), при этом типы защелки используются в устройствах под напряжением или при отключении питания. Линейные соленоиды также могут быть разработаны для пропорционального управления движением, где положение плунжера пропорционально потребляемой мощности. Когда электрический ток протекает через проводник, он генерирует магнитное поле, и направление этого магнитного поля относительно его северного и южного полюсов определяется направлением потока тока внутри провода.
Эта катушка проволоки становится « электромагнитом » со своими собственными северным и южным полюсами, точно такими же, как у постоянного магнита. Сила этого магнитного поля может быть увеличена или уменьшена либо путем управления количеством тока, протекающего через катушку, либо путем изменения количества витков или петель, которые имеет катушка. Пример «электромагнита» приведен ниже.
Рекомендации
- Кембриджский словарь для продвинутых учащихся
дает два фонетических варианта /ˈsəʊ.lə.nɔɪd/ и /ˈsoʊ.lə.nɔɪd/.«Соленоид: значение в Кембриджском словаре английского языка».
Dictionary.cambridge.org
. В архиве из оригинала 16 января 2022 г.. Получено 16 января 2017. - Французский термин был придуман в 1823 году от σωλήν «канал, труба» и -оид (-o-ειδής) суффикс. «Соленоид» в: Trésor de la langue française informatisé
. Греческое σωληνοειδ, «форма трубы», впервые засвидетельствовано в Эней Тактик (4 век до нашей эры). Генри Джордж Лидделл, Роберт Скотт,
Греко-английский лексикон
(1843). Смотрите также «Соленоид».
Интернет-словарь этимологии
. В архиве из оригинала 28 июля 2011 г. - Сессия Академия наук
от 22 декабря 1823 г., напечатано в: Ampère, «Mémoire sur la théorie mathématique des phénomènes électro-Dynamiques»,
Mémoires de l’Académie royale des Sciences de l’Institut de France
6 (1827 г.), Париж, Ф. Дидо, С. 267ff. (и инжир. 29–33). «l’assemblage de tous les circuit qui l’entourent [а именно l’arc], Assemblage auquel j’ai donné le nom de
соленоид электро-динамический
, du mot grec σωληνοειδὴς, dont laignation exprime précising ce qui a la forme d’un canal, c’est-à-dire la surface de cette forme sur laquelle se Trouvent tous les circuit »(стр. 267). - или, что то же самое, диаметр катушки предполагается бесконечно малым (Ampère 1823, p. 267: «des courants électriques formants de très-petits circuit autour de cette ligne, dans des plan infiniment rapprochés qui lui soient perpendiculaires»).
- [[1]]
- Джайлз, Дэвид. Введение в магнетизм и магнитные материалы. CRC press, стр. 48, 2015.
- «Архивная копия» (PDF). В архиве (PDF) из оригинала 10 апреля 2014 г.. Получено 28 марта 2013.CS1 maint: заархивированная копия как заголовок (ссылка на сайт)
- Мюллер, Карл Фридрих (1 мая 1926 г.). «Berechnung der Induktivität von Spulen» [Расчет индуктивности катушек]. Archiv für Elektrotechnik
(на немецком).
17
(3): 336–353. Дои:10.1007 / BF01655986. ISSN 1432-0487. S2CID 123686159. - Каллаган, Эдмунд Э .; Маслен, Стивен Х. (1 октября 1960 г.). «Магнитное поле конечного соленоида». Технические отчеты НАСА
. НАСА-TN-D-465 (E-900). - Качагли, Алессио; Baars, Roel J .; Филипс, Альберт П .; Kuipers, Bonny W.M. (2018). «Точное выражение для магнитного поля конечного цилиндра с произвольной однородной намагниченностью». Журнал магнетизма и магнитных материалов
.
456
: 423–432. Дои:10.1016 / j.jmmm.2018.02.003. ISSN 0304-8853. - Курс, Андре; Каралис, Аристеидис; Моффатт, Роберт; Joannopoulos, J.D .; Фишер, Питер; Солячич, Марин (6 июля 2007 г.). «Беспроводная передача энергии с помощью сильносвязанных магнитных резонансов». Наука
.
317
(5834): 83–86. Дои:10.1126 / science.1143254. PMID 17556549. S2CID 17105396. - Чжоу, Вэньшэнь; Хуан, Шао Ин (28 сентября 2022 г.). «Новая конструкция катушки для широкополосной беспроводной передачи энергии». Симпозиум Международного общества прикладных вычислительных электромагнетиков (ACES) 2022 г.
. - Рен, Чжи Хуа; Хуан, Шао Ин (август 2022 г.). «Конструкция короткого соленоида с однородным B1 для портативного магнитно-резонансного томографа с низким полем с использованием генетического алгоритма». Proc. 26-я ISMRM
: 1720. - Jian, L .; Shi, Y .; Liang, J .; Liu, C .; Сюй, Г. (июнь 2013 г.). «Новая система направленной магнитной жидкостной гипертермии, использующая массив катушек HTS для лечения опухолей». IEEE Transactions по прикладной сверхпроводимости
.
23
(3): 4400104. Дои:10.1109 / TASC.2012.2230051. S2CID 44197357. - Чжоу, Вэньшэнь; Хуан, Шао Ин (июль 2022 г.). «Точная модель для быстрого вычисления резонансной частоты нерегулярного соленоида». Протоколы IEEE по теории и методам микроволнового излучения
.
67
(7): 2663–2673. Дои:10.1109 / TMTT.2019.2915514. S2CID 182038533. - Чжоу, Вэньшэнь; Хуан, Шао Ин. «Код точной модели для быстрого расчета резонансной частоты нерегулярного соленоида». Цитировать журнал требует | журнал = (Помогите)
- Чжоу, Вэньшэнь; Хуан, Шао Ин (октябрь 2022 г.). «Моделирование собственной емкости нерегулярного соленоида». IEEE Transactions по электромагнитной совместимости
: 1–9. Дои:10.1109 / TEMC.2020.3031075. - Чжоу, Вэньшэнь; Хуан, Шао Ин. «Код точной модели для определения собственной емкости нестандартных соленоидов». Цитировать журнал требует | журнал = (Помогите)
- Д. Ховард Деллинджер; Л. Э. Уиттмор и Р. С. Ульд (1924). Радио инструменты и измерения
.
Циркуляр NBS
.
C74
. ISBN 9780849302527 . Получено 7 сентября 2009. - «Как держать звонок в дверь». Популярная наука
(Март 1975 г.). Март 1975. с. 117. В архиве из оригинала 14 мая 2018 г.. Получено 29 ноября 2022.
внешняя ссылка
| Викискладе есть медиафайлы по теме Соленоиды . |
- Интерактивное руководство по Java: Магнитное поле соленоида, Национальная лаборатория сильных магнитных полей
- Обсуждение соленоидов в гиперфизике
- Основы соленоидов для робототехники
- Основы вращающихся звуковых катушек
- Что такое соленоид
- Как работает соленоид постоянного тока
- [2] Macro Magnetics.pdf; Расчет сил соленоида
| Авторитетный контроль |
|
Простые драйверы для соленоидов
Самый простой способ управлять соленоидом — включить и выключить ток. Это часто делается с помощью переключателя MOSFET с низкой стороны и токового защитного диода (рисунок ниже). В этой схеме ток ограничен только напряжением питания и постоянным сопротивлением соленоида.
Электромеханические характеристики простого привода соленоида ограничены. Поскольку полное напряжение и ток применяются в течение 100% времени, ток втягивания ограничивается постоянной мощностью рассеяния соленоида. Большая индуктивность катушки ограничивает скорость нарастания тока при включении соленоида.
В тесте измерялось движение, напряжение и ток соленоида включаемого с помощью простого переключателя (рисунок ниже). В этом случае время включения соленоида (15 Ом, рассчитанного на 12 В) занимало 30 мс, чтобы приводить в действие механический привод и рассеивать мощность 10 Вт.
Если вы задаетесь вопросом о «впадине» в текущей форме волны, то это уменьшение тока связано с обратной ЭДС, создаваемой движущимся сердечником соленоида. Обратная ЭДС увеличивается по мере того, как сердечник разгоняется до тех пор, пока соленоид не втянется и не остановится.