Системы оповещения, профессиональное звуковое оборудование, конференц-системы

Средняя оценка: 4.6

Всего получено оценок: 79.

4.6

Средняя оценка: 4.6

Всего получено оценок: 79.

Сопротивление проводника ограничивает величину тока в электрической цепи. Чем больше величина сопротивление, тем меньше ток. Расчет сопротивления проводника можно произвести двумя способами: первый способ заключается в использовании формулы закона Ома, а второй вариант расчета подразумевает знание геометрических размеров проводника и удельного сопротивления вещества, из которого он сделан.

Почему проводник “сопротивляется”?

Напряжение U, поданное на концы проводника, создает внутри него электрическое поле, которое приводит в движение свободные электроны вещества. Электроны, получив дополнительную кинетическую энергию, начинают двигаться упорядоченно в одном направлении, создавая тем самым электрический ток цепи.

В процессе движения электроны сталкиваются с нейтральными и заряженными атомами, из которых стоит проводник, теряют энергию. Масса атома превосходит массу электрона в тысячи раз, поэтому их столкновение приводит к изменению направления движения электронов и потере скорости (“торможению”).

Таким образом возникает сопротивление протеканию (нарастанию) тока. Рис. 1. Электрический ток в проводнике ограничивается столкновением электронов с атомами.

Особенности активного сопротивления

Сопротивление в электротехнике является важнейшим параметром, с помощью которого какая-то часть электрической цепи оказывает противодействие проходящему по ней току. Образованию данной величины способствуют изменения электроэнергии и ее переход в другие виды энергетических состояний.

Данное явление в полной мере затрагивает любые виды провода и кабеля. При одинаковых условиях, они будут по-разному сопротивляться прохождению постоянного и переменного тока. Подобная ситуация возникает из-за неравномерного распределения переменного тока по сечению проводника, в результате чего образуется так называемый поверхностный эффект.

Расчет сопротивления с помощью закона Ома

Немецкий физик Георг Ом в 1826 г. обнаружил, что отношение напряжения U между концами металлического проводника, являющегося участком электрической цепи, к силе тока I есть величина постоянная:

$ R={U \over I}=const $ (1),

где:

U — напряжение, В;

I — сила тока, А;

R — сопротивление, Ом.

Эту величину стали называть электрическим сопротивлением. Пользуясь этой формулой, можно экспериментально определить величину неизвестного сопротивления.

Для этого амперметром измеряется величина электрического тока через сопротивление, а вольтметром — напряжение на участке цепи. Далее, применяя формулу (1), вычисляется значение R.

Единица измерения названа в честь Георга Ома. Электрическим сопротивлением 1 Ом обладает участок цепи, на котором при силе тока 1 А напряжение равно 1 В:

$$ 1 Ом = { 1 В\over 1 A} $$

Определение активного сопротивления проводов

Активное сопротивлении проводов проще всего определять по справочным данным, составленным на основании ГОСТ 839-80 – «Провода неизолированные для воздушных линий электропередач» таблицы 1 – 4. Данные таблицы вы сможете найти непосредственно в самом ГОСТ, приведу лишь не которые.

Пользоваться всеми известными формулами по определению активного сопротивления — не рекомендуется [Л1. с.18],связано это с тем, что действительное сечение отличается от номинального сечения, провода выпускались в разное время, по разным ГОСТ и ТУ и величины удельной проводимости (ρ) и удельного сопротивления (γ) у них разные:

где:

• γ – значение удельной проводимости для медных и алюминиевых проводов при температуре 20 °С принимается: для медных проводов – 53 м/Ом*мм2; для алюминиевых проводов – 31,7 м/Ом*мм2;
• s – номинальное сечение провода(кабеля),мм2;
• l – длина линии, м;
• ρ – значение удельного сопротивления принимается: для медных проводов — 0,017-0,018 Ом*мм2/м; для алюминиевых проводов – 0,026 — 0,028 Ом*мм2/м, см. таблицу 1.14 [Л2. с.30].

Активные сопротивления стальных проводов математическому расчету не поддаются. Поэтому рекомендую для определения активного сопротивления использовать приложения П23 – П25 [Л1. с.80,81].

Расчет с помощью удельного сопротивления

Расчет сопротивления проводника можно произвести без измерения величин напряжения и тока. Но для этого необходимо знать дополнительную информацию о проводнике.

Георг Ом и другие исследователи опытным путем определили, что сопротивление проводника прямо пропорционально длине проводника L и обратно пропорционально площади поперечного сечения проводника S. Эту закономерность можно описать формулой расчета сопротивления проводника:

$ R = ρ *{ L\over S} $ (2)

Коэффициент ρ был назван удельным сопротивлением. Эта физическая величина отражает особенности конкретного вещества, которые зависят от плотности вещества, кристаллической структуры, строения атомов и других внутренних параметров. Расчет удельного сопротивления проводника производить каждый раз необязательно, так как для большинства веществ удельные сопротивления измерены и сведены в справочные таблицы, которые можно найти в бумажных справочниках или в их интернет-версиях.

Но если такая необходимость возникнет, то из формулы (2) можно получить следующую формулу (3), и по ней рассчитать ρ:

$ ρ = R*{ S\over L } $ (3)

Серебро имеет одно из самых низких значений ρ, равное $ 0,016 {Ом*мм^2\over м} $. Этим объясняется использование такого довольно дорогого металла для пайки особенно важных радиодеталей (микросхем, микропроцессоров, электронных плат), которые должны как можно меньше нагреваться в процессе работы.

Расчет сечения жилы провода в зависимости от длины и нагрузки в линии

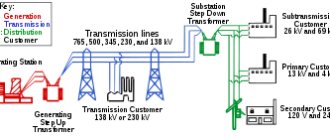
В любой линии связи возникают потери. Линия – жила медного провода имеет определенное сопротивление, зависящее от длины, и, следовательно, по закону Кирхгофа на ней должно упасть напряжение и выделиться определенная мощность. В трансляционных системах в качестве нагрузки используются трансформаторные громкоговорители. Импеданс трансформаторного громкоговорителя Z – сопротивление первичной обмотки трансформатора на частоте 1кГц. Сопротивление нагрузки, линии является частотно зависимой (комплексной) величиной, поэтому в этом случае выполняют элементарный оценочный расчет, для среднегеометрической частоты всего частотного диапазона (большинство производителей импеданс трансформаторного громкоговорителя указывают для частоты 1кГц, что соответствует середине нормативного частотного диапазона 0,2 – 5кГц).

Задачу определения сечения жилы провода будем решать в 2 этапа, используя известное представление линии и нагрузки, в виде резистивного делителя (см. рис.2).

Первый этап, на котором вся нагрузка сосредоточена в конце линии, позволит упростить решение задачи и перейти ко 2 этапу, на котором будут доопределены коэффициенты, позволяющие рассчитывать сечение жилы провода в распределенной линии с произвольно задаваемыми потерями.

Входные данные для расчета:

Рн – мощность нагрузки в линии, Вт;

Uвх – напряжение на входе линии, В;

L – общая протяженности линии, м.

Для определения сечения жилы провода S, воспользуемся эмпирическими соображениями. Из электроакустики известно, что для сохранения качества передаваемого звукового сигнала, величина потерь по напряжению в линии не должна превышать 10% (данная величина соответствует потерям по мощности примерно 20%, что принято считать нормой), что для резистивного делителя (см. рис. 2), можно записать как: Rл ~ 0,1 Rн, где Rн – сопротивление нагрузки, Ом.

Подставим данное соотношение в формулу (3):

В трансляционных линиях нагрузкой являются трансформаторные громкоговорители. В этом случае в качестве сопротивления нагрузки Rн можно принять значение импеданса громкоговорителя на определенной частоте. Импеданс трансформаторного громкоговорителя Zгр представляет собой частотно-зависимое (комплексное) сопротивление первичной обмотки звукового трансформатора. Большинство производителей трансформаторных громкоговорителей указывают значение импеданса для максимальной мощности на частоте 1кГц.

Импеданс трансформаторного громкоговорителя Zгр можно получить из 2-х известных формул:

1. Закона Ома для участка цепи : J = U / R,
2. Мощности нагрузки: P = JU.

При использовании в качестве нагрузки нескольких параллельно подключенных трансформаторных громкоговорителей суммарный импеданс Z рассчитывается по формуле:

Формула (7), определяющая проводимость всей цепи, неудобна для расчета суммарного нагрузочного импеданса, особенно, для трансляционной линии с большим количеством громкоговорителей разной мощности. Для расчета суммарного импеданса Z нескольких трансформаторных громкоговорителей удобно использовать формулу (6), в которой Pгр необходимо заменить суммарной мощностью всех трансформаторных громкоговорителей Pн, состоящей из суммы мощностей отдельных громкоговорителей Pi:

Используя в качестве сопротивления нагрузки Rн суммарный импеданс трансформаторных громкоговорителей Z (7) и подставляя (6) в (5), получаем полезную формулу, определяющую сечение жилы провода S в зависимости от мощности нагрузки Рн, напряжения на входе Uвх и длины линии L:

Формула (9) справедлива при потерях в линии, не превышающих 10% и условии, что вся нагрузка сосредоточена в конце линии (формула 8 очень эффективна для протяженных линии (L более 150м). На коротких линиях (L менее 150м) не следует забывать о соотношении сечения и нормы тока (формула 2).

Закон Ома для цепи переменного тока

В цепи переменного тока сопротивление кроме активной, может иметь как емкостную, так и индуктивную составляющие. Рассмотрим цепь переменного тока, состоящую из резистора сопротивлением R, конденсатора емкостью C и катушки индуктивностью L, соединенных последовательно.

Мгновенные значения силы тока на всех элементах этой цепи одинаковы, а мгновенное значение напряжения между концами цепи равно алгебраической сумме мгновенных значений напряжений на резисторе (UR), конденсаторе (UC) и катушке индуктивности (UL).

Для того чтобы определить амплитудные (или действующие) значения напряжения и силы тока, а также сдвиг фаз между ними удобно использовать метод векторных диаграмм. Здесь действующие значения всех напряжений и токов рассматриваются как векторы, вращающиеся с угловой скоростью ω, равной циклической частоте переменного тока, а их мгновенные значения определяются проекциями этих векторов на горизонтальную ось. Так как сила тока в цепи одинакова, то построение векторной диаграммы начинается с вектора I¯0, модуль которого равен амплитудному значению силы тока в цепи. Направление этого вектора может быть любым. Зададим угол α = ωt к горизонтали.

Колебания напряжения на активном сопротивлении совпадают по фазе с колебаниями силы тока, поэтому вектор U¯0R, модуль которого равен U0R = I0 × R, совпадает по направлению с вектором I¯0. Сдвиг фаз между колебаниями силы тока и колебаниями напряжения на индуктивном сопротивлении составляет π / 2, причем ток отстает по фазе от напряжения. Поэтому вектор U¯0L, модуль которого равен U0L = I0 × ωL, нужно повернуть относительно вектора I¯0 на угол π / 2 против часовой стрелки. Вектор U¯0C, модуль которого равен I0 / ωC, отстает по фазе от вектора I¯0 на π / 2, поэтому его нужно повернуть на этот угол по часовой стрелке.

Для того чтобы найти напряжение на зажимах цепи, необходимо сложить три вектора: U¯0 = U¯0R + U¯0L + U¯0C.

В первую очередь сложим векторы U¯0R и U¯0C. Модуль этой суммы U’0 = [U¯0R + U¯0C]. Пусть ωL > 1 / ωC, тогда: U’0 = I0 × (ωL — 1 / ωC).

Теперь сложим векторы U¯0R и U’¯0. Модуль вектора U¯0 определяется по теореме Пифагора: U0² = U0R² + (U0L — U0C)² = I0² × R² + I0² × (ωL — 1 / ωC)². Соответственно амплитудное (действующее) значение силы тока в цепи переменного тока равно отношению амплитудного (действующего) значения напряжения на концах этой цепи к его полному сопротивлению (закон Ома для цепи переменного тока):

I0 = U0 / √(R² + (ωL — 1 / ωC)²) = U0 / Z, где:

• Z — полное сопротивление (импеданс) цепи.
• R — его активное сопротивление.
• ωL — 1 / ωC — реактивное сопротивление цепи переменного тока.
• ω = 2 × π × γ — циклическая, угловая частота. γ — частота переменного тока.

Импеданс при параллельном подключении Z = 1 / √(1 / R² + 1 / (1 / ωL — ωC)²).

Сдвиг фаз между силой тока и напряжением равен углу φ между векторами U¯0 и I¯0. В соответствии с графиком выше ток отстает от напряжения на угол φ, причем tgφ = (ωL — 1 / ωC) / R.

Для того чтобы определить мгновенные значения напряжений на активном, емкостном и индуктивном сопротивлениях, необходимо спроектировать векторы U¯0R, U¯0L, U¯0C на прямую АВ.

Тогда:

• UR = I0 × R × sin × (ωt + φ).
• UL = I0 × ωL × sin × (ωt + φ + π / 2).
• UC = (I0 / ωС) × sin × (ωt + φ — π / 2).

Если 1 / ωС > ωL, то:

• U’0 = I0 × (1 / ωС — ωL).
• tgφ = (1 / ωC — ωL) / R, причем ток опережает напряжение по фазе на угол φ.