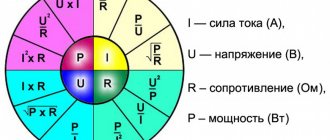
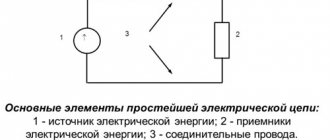
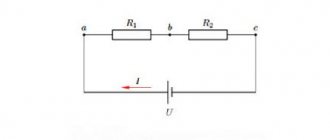
На практике часто встречаются задачи по расчётам параметров токов и напряжений в различных разветвлённых цепях. В качестве инструмента для расчётов используют правила Кирхгофа (в некоторой литературе их называют еще законами, хотя это не совсем корректно) – одни из фундаментальных правил, которые совместно с законами Ома позволяет определять параметры независимых контуров в самых сложных цепях.
Учёный Густав Киргхоф сформулировал два правила [], для понимания которых введено понятие узла, ветви, контура. В нашей ситуации ветвью будем называть участок, по которому протекает один и тот же ток. Точки соединения ветвей образуют узлы. Ветви вместе с узлами образуют контуры – замкнутые пути, по которым течёт ток.
Первое правило Кирхгофа
Первое правило Густава Кирхгофа сформулировано исходя из закона сохранения заряда. Физик понимал, что заряд не может задерживаться в узле, а распределяется по ветвям контура, образующим это соединение.
Кирхгоф предположил, а впоследствии обосновал на основании экспериментов, что количество зарядов зашедших в узел такое же, как и количество тока вытекающего из него.
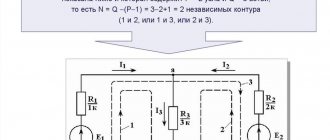
На рисунке 1 изображена простая схема, состоящая из контуров. Точками A, B, C, D обозначены узлы контура в центре схемы.
Рис. 1. Схема контура
Ток I1 входит в узел A, образованный ветвями контура. На схеме электрический заряд распределяется в двух направлениях – по ветвям AB и AD. Согласно правилу Кирхгофа, входящий ток равен сумме выходящих: I1 = I2 + I3.
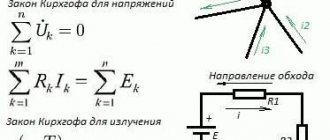
На рисунке 2 представлен абстрактный узел, по ветвям которого течёт ток в разных направлениях. Если сложить векторы i1, i2, i3, i4 то, согласно первому правилу Кирхгофа, векторная сумма будет равняться 0: i1 + i2 + i3 + i4 = 0. Ветвей может быть сколько угодно много, но равенство всегда будет справедливым, с учётом направления векторов.
Рис. 2. Абстрактный узел
Запишем наши выводы в алгебраической форме, для общего случая:
Для использования этой формулы, требуется учитывать знаки. Для этого необходимо выбрать направление одного из векторов тока (не важно, какого) и обозначить его знаком «плюс». При этом знаки всех других величин определить, исходя от их направления, по отношению к выбранному вектору.
Чтобы избежать путаницы, ток, направленный в точку узла, принято считать положительным, а векторы, направленные от узла – отрицательными.
Изложим первое правило Кирхгофа, выраженное приведённой выше формулой: «Алгебраическая сумма сходящихся в определённом узле токов, равна нулю, если считать входящие токи положительными, а отходящими – отрицательными».
Первое правило дополняет второе правило, сформулированное Кирхгофом. Перейдём к его рассмотрению.
Разветвленные цепи. Правила Кирхгофа.
Законы Кирхгофа
для разветвленной цепи (разветвленная цепь – электрическая цепь, содержащая узлы – места, где сходятся не менее трех проводников):
а) По первому закону Кирхгофа
–
алгебраическая сумма токов, сходящихся в узле, равна нулю
. Токи, приходящие к узлу, считаются положительными, а токи, отходящие от узла, отрицательными.
б)Второй закон Кирхгофа
:
в замкнутом контуре алгебраическая сумма произведений токов в участках на сопротивление этих участков равна алгебраической сумме электродвижущих сил, включенных в данный контур
,
где – алгебраическая сумма сил токов, сходящихся в узле; – алгебраическая сумма произведений сил токов на сопротивления замкнутых участков; – алгебраическая сумма ЭДС источников тока на замкнутом участке цепи.
При расчете сложных цепей постоянного тока с применением правил Кирхгофа необходимо:
1. Выбрать произвольное направление токов на всех участках цепи.
2. Выбрать направление обхода контура; произведение положительно, если ток на участке совпадает с направлением обхода, и, наоборот; ЭДС, действующие по выбранному направлению обхода (перемещение происходит внутри источника тока от катода к аноду), считаются положительными.
3. Составить столько уравнений, чтобы их число было равно числу неизвестных электрических величин; каждый рассматриваемый контур должен содержать хотя бы один элемент, не содержавшийся в предыдущих контурах.
Первое правило Кирхгофа:
алгебраическая сумма токов, сходящихся в узле, равна нулю:
Например, для рис. 148 первое правило Кирхгофа запишется так:
Первое правило Кирхгофа вытекает из закона сохранения электрического заряда. Действительно, в случае установившегося постоянного тока ни в одной точке проводника и ни на одном его участке не должны накапливаться электрические заряды. В противном случае токи не могли бы оставаться постоянными.
Второе правило Кирхгофа получается из обобщенного закона Ома для разветвленных цепей. Рассмотрим контур, состоящий из трех участков (рис. 149). Направление обхода по часовой стрелке примем за положительное, отметив, что выбор этого направления совершенно произволен. Все токи, совпадающие по направлению с направлением обхода контура, считаются положительными, не совпадающие с направлением обхода — отрицательными. Источники тока считаются положительными, если они создают ток, направленный в сторону обхода контура. Применяя к участкам закон Ома (100.3), можно записать:
Складывая почленно эти уравнения, получим
(101.1)
Уравнение (101.1) выражает второе правило Кирхгофа
: в любом замкнутом контуре, произвольно выбранном в разветвленной электрической цепи, алгебраическая сумма произведений сил токов
Ii
на сопротивления
Ri
соответствующих участков этого контура равна алгебраической сумме э.д.с. , встречающихся в этом контуре:
(101.2)
При расчете сложных цепей постоянного тока с применением правил Кирхгофа необходимо:
1. Выбрать произвольное
направление токов на всех участках цепи; действительное направление токов определяется при решении задачи: если искомый ток получится положительным, то его направление было выбрано правильно, отрицательным — его истинное направление противоположно выбранному.
2. Выбрать направление обхода контура и строго его придерживаться; произведение IR
положительно, если ток на данном участке совпадает с направлением обхода, и, наоборот, э.д.с., действующие по выбранному направлению обхода, считаются положительными, против — отрицательными.
3. Составить столько уравнений, чтобы их число было равно числу искомых величин (в систему уравнений должны входить все сопротивления и э.д.с. рассматриваемой цепи); каждый рассматриваемый контур должен содержать хотя бы один элемент, не содержащийся в предыдущих контурах, иначе получатся уравнения, являющиеся простой комбинацией уже составленных.
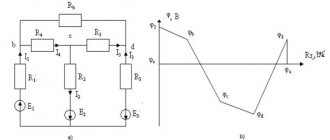
В качестве примера использования правил Кирхгофа рассмотрим схему (рис. 150) измерительногомоста Уитстона.
* Сопротивления
R
1
, R
2
, R
3и
R
4 образуют его «плечи». Между точками
А
и
В
моста включена батарея с э.д.с. и сопротивлением
r
, между точками
С
и
D
включен гальванометр с сопротивлением
RG.
Для узлов
А, В
и
С,
применяя первое правило Кирхгофа, получим
(10 1.3)
Для контуров АСВA, ACDA
и
CBDC,
согласно второму правилу Кирхгофа, можно записать:
(101.4)
* Ч. Уитстон (1802—1875) — английский физик.
Если известны все сопротивления и э.д.с., то, решая полученные шесть уравнений, можно найти неизвестные токи. Изменяя известные сопротивления R
2,
R
3 и
R
4
,
можно добиться того, чтобы ток через гальванометр был равен нулю (
IG
= 0)
.
Тогда из (101.3) найдем
(101.5)
а из (101.4) получим
(101.6)
Из (101.5) и (101.6) вытекает, что
(101.7)
Таким образом, в случае равновесного моста (IG
= 0) при определении искомого сопротивления
R
1 э.д.с. батареи, сопротивления батареи и гальванометра роли не играют.
На практике обычно используетсяреохордный мост Уитстона
(рис. 151), где сопротивления
R
3и
R
4 представляют собой длинную однородную проволоку (реохорд) с большим удельным сопротивлением, так что отношение
R
3
/R
4 можно заменить отношением
l
3/
l
4. Тогда, используя выражение (101.7), можно записать
(101.
Длины l
3 и
l
4 легко измеряются по шкале, a
R
2 всегда известно. Поэтому уравнение (101.8) позволяет определить неизвестное сопротивление
R
1.
РАЗВЕТВЛЕННЫЕ ЦЕПИ
Параллельное соединение приемников. Вначале рассмотрим графоаналитический метод расчета цепи с параллельным соединением потребителей (рис. 2.16, а
). Для такой цепи характерно то, что напряжения на каждой ветви одинаковы, общий ток равен сумме токов ветвей.
Ток в каждой ветви определяется по закону Ома:
| I 1 = | U | ; I 2 = | U | ; I 3 = | U | (xL 3 > xC 3). |
| √r 12 + xL 12 | √r 22 + xC 22 | √r 32 + ( xL 3 — xC 3)2 |
Угол сдвига φ между током каждой ветви и напряжением определяют с помощью cos φ:
| cos φ1 = | r 1 | ; cos φ2 = | r 2 | ; cos φ3 = | r 3 | . |
| √r 12 + xL 12 | √r 22 + xC 22 | √r 32 + ( xL 3 — xC 3)2 |
|
Общий ток в цепи, как следует из первого закона Кирхгофа, равен геометрической сумме токов всех ветвей:
Ī
=
Ī
1 +
Ī
2 +
Ī
3.
Значение общего тока определяют графически по векторной диаграмме рис. 2.16, б
.
Активная мощность цепи равна арифметической сумме активных мощностей всех ветвей:
Р = Р
1
+ P
2
+ P
3
.
Реактивная мощность цепи равна алгебраической сумме реактивных мощностей всех ветвей:
| n | ||
| Q = | ∑ | Qk . |
причем реактивную мощность ветви с индуктивностью берут со знаком плюс, ветви с емкостью — со знаком минус. Для цепи рис. 2.16 реактивная мощность равна
Q
=
QL
1 —
QC
2 +
QL
3 —
QC
3.
Полная мощность цепи
S = √P
2 +
Q
2.
Угол сдвига φ между общим током и напряжением определяют из векторной диаграммы или из выражения:
cos φ = P/S.
Графоаналитический метод не удобен для расчета разветвленных цепей: он отличается громоздкостью и невысокой степенью точности.
Для анализа и расчета разветвленных цепей переменного тока используют проводимости, с помощью которых разветвленную цепь можно преобразовать в простейшую цепь и аналитически рассчитать токи и напряжения всех ее участков.
В цепях постоянного тока проводимостью называется величина, обратная сопротивлению участка цепи:
g
= 1/
r
и ток в цепи выражается как произведение напряжения на проводимость:
I = Ug.
| Рис. 2.17. Электрическая цепь (а ), ее векторная диаграмма ( б ) и эквивалентная схема ( в ); векторная диаграмма цепи при резонансе |
В цепях переменного тока существуют три проводимости — полная,
активная и реактивная, причем только полная проводимость является величиной, обратной полному сопротивлению последовательного участка цепи.
Выражения проводимостей в цепях переменного тока можно получить следующим образом.
Ток в каждом неразветвленном участке цепи раскладывают на две составляющие, одна из которых есть проекция на вектор напряжения (активная составляющая тока I
a ), а другая — на линию, перпендикулярную вектору напряжения (реактивная составляющая тока
I
р ).
Активная составляющая тока определяет активную мощность
P
=
UI
cos φ =
UI
a ;
реактивная составляющая тока — реактивную мощность
Q = UI
sin φ =
UI
р.
Из векторной диаграммы цепи рис. 2.17, а
, изображенной на рис. 2.17,
б
, следует, что активная составляющая тока
I
1 равна
| I 1a = I 1 cos φ1 = | U | r | = Ur 1 /z 12 = Ug 1 . |
| z 1 | z 1 |
Величина
g
1 =
r
1
/z
12
называется активной проводимостью ветви. Реактивная составляющая тока I
1 равна
| I lp = I 1 sin φ1 = | U | xL | = UxL/z 12 = Ub 1. |
| z 1 | z 1 |
Величина
b
1 =
xL/z
12 =
bL
1
называется реактивной проводимостью ветви цепи с индуктивностью и в общем случае обозначается bL.
Аналогично определяют активную g
2 и реактивную
b
2 проводимости второй ветви цепи:
I
2а =
I
2cos φ2 =
U/z
2 •
r
2
/z
2
= Ug
2 ;
g
2
=r
2
/z
22 ;
I
2p =
I
2 sin φ2 =
U/z
2•
xC /z
2
= Ub
2;
b
2
= bC
2
= xC
2
/z
22
.
Реактивная проводимость ветви с емкостью в общем случае обозначается bC.
Вектор тока первой ветви равен геометрической сумме векторов активной и реактивной составляющих тока
Ī
1 =
Ī
1а +
Ī
1р,
а значение тока
I
1 = √
I
1а2 +
I
1р2.
Выразив составляющие тока через напряжение и проводимости, получим
I
1 = √(
Ug
1)2 + (
UbL
1)2
= U
√
g
12 +
bL
12 =
Uу
1
= U/z
1
,
где у
1 = 1
/z
1
=
√
g
12 +
bL
12 — полная проводимость ветви.
Аналогично определяют и полную проводимость второй ветви:
у
2
=
1
/z
2
=
√
g
22 +
bС
2.
Эквивалентные активную, реактивную и полную проводимости цепи получают следующим образом.
Вектор общего тока цепи равен геометрической сумме векторов токов Ī
1 и
Ī
2:
Ī
=
Ī
1
+ Ī
2
и может быть выражен через активную и реактивную составляющие тока и эквивалентные проводимости всей цепи:
Ī
=
Ī
а +
Ī
р
= Ūg
э +
Ūb
э =
Uу
э
= U/z
э
.
Активная составляющая общего тока (см. рис. 2.17, б
) равна арифметической сумме активных составляющих токов ветвей:
(2.24)
I
а =
I
1а +
I
2а =
Ug
1 +
Ug
2 =
U
(
g
1 +
g
2) =
Ug
э
.
а реактивная составляющая — арифметической разности реактивных составляющих этих токов:
(2.25)
I
р =
I
1р +
I
2р =
UbL
1
— UbC
2 =
U
(
bL
1
— bC
2)=
Ub
э .
| Рис. 2.18. К расчету разветвлен- ной цепи с использова- нием проводимостей |
Из выражений (2.24) и (2.25) следует, что эквивалентная активная проводимость цепи равна арифметической сумме активных проводимостей параллельно включенных ветвей:
(2.26)
g
э =
g
1 +
g
2 + …
+ gn
,
а эквивалентная реактивная проводимость — алгебраической сумме реактивных проводимостей параллельно включенных ветвей:
(2.27)
b
э =
bL
1 +
bС
2
+ …
+
bLn + bСп .
При этом проводимости ветвей с индуктивным характером нагрузки берут со знаком плюс, ветвей с емкостным характером нагрузки — со знаком минус. Полная эквивалентам проводимость цепи
(2.28)
у
э
=
1/zэ = √
g
э2 +
b
э2
.
По эквивалентным активной, реактивной и полной проводимостям можно определить параметры эквивалентной схемы (рис. 2.17, в) цепи.
Эквивалентные активное, реактивное и полное сопротивления цепи определяют с помощью выражений
z
э = 1/
у
э ,
r
э =
g
э
z
э2
, х
э =
b
э
z
э2.
Необходимо отметить, что если ΣbL
> Σ
bC
, то эквивалентное сопротивление
х
э будет индуктивным, если Σ
bC
> Σ
bL —
емкостным.
Смешанное соединение потребителей.
Расчет цепи при смешанном соединении потребителей (рис. 2.18,
а
) может быть произведен путем замены ее простейшей эквивалентной цепью. Для этого вначале определяют активные, реактивные и полные проводимости параллельно включенных ветвей:
g
1,
g
2,
b
1,
b
2,
у
1,
у
2.
Затем находят эквивалентные активную, реактивную и полную проводимости параллельного участка цепи:
g
э
= g
1+
g
2;
b
э
= b
1
+ b
2;
у
э
=
√
g
э2 +
b
э2.
Далее определяют эквивалентные активное, реактивное и полное сопротивления параллельного участка цепи:
r
э =
g
э
z
э2;
x
э =
b
э
z
э2;
z
э = 1/
у
э.
В результате расчетов цепь может быть заменена эквивалентной цепью (рис. 2.18, б
), где все сопротивления включены последовательно. Общие активное, реактивное и полное сопротивления цепи равны
r
об =
r
э +
r. x
об =
x ± x
э,
z
об = √
r
об2 +
x
об2.
Цепь приобретает простейший вид, изображенный на рис. 2.18, в. Общий ток цепи определяют по закону Ома:
I = U
/
z
об
Напряжение между точками а и b
Uab = Iz
э
= I/у
э
.
Токи в параллельных ветвях равны
I
1
= Uab у
1,
I
2
= Uab у
2.
Второе правило Киргхофа
Из третьего уравнения Максвелла вытекает правило Кирхгофа для напряжений. Его ещё называют вторым законом.
Это правило гласит, что в замкнутом контуре, на резистивных элементах, алгебраическая сумма напряжений (включая внутренние), равна сумме ЭДС, присутствующих в этом же замкнутом контуре.
При этом токи и ЭДС, векторы которых совпадают с направлением (выбирается произвольно) обхода контура, считаются положительными, а встречные к обходу токи – отрицательными.
Рис. 4. Иллюстрация второго правила Кирхгофа
Формулы, которые изображены на рисунке применяются в частных случаях для вычисления параметров простых схем.
Формулировки уравнений общего характера:
, где где Lk и Ck – это индуктивности и ёмкости, соответственно.
Линейные уравнения справедливы как для линейных, так и для нелинейных линеаризованных цепей. Они применяются при любом характере временных изменений токов и напряжений, для разных источников ЭДС. При этом законы Кирхгофа справедливы и для магнитных цепей. Это позволяет выполнять вычисления для поиска соответствующие параметров.
Что такое правило напряжений Кирхгофа (второй закон Кирхгофа)?
Принцип, известный как правило напряжений Кирхгофа (открытое в 1847 году немецким физиком Густавом Р. Кирхгофом), можно сформулировать следующим образом:
«Алгебраическая сумма всех напряжений в замкнутом контуре равна нулю»
Под алгебраической я подразумеваю, помимо учета величин, учет и знаков (полярностей). Под контуром я подразумеваю любой путь, прослеживаемый от одной точки в цепи до других точек в этой цепи, и, наконец, обратно в исходную точку.
Закон Кирхгофа для магнитной цепи
Применение независимых уравнений возможно и при расчётах магнитных цепей. Сформулированные выше правила Кирхгофа справедливы и для вычисления параметров магнитных потоков и намагничивающих сил.
Рис. 4. Магнитные контуры цепей
В частности: ∑Ф=0.
То есть, для магнитных потоков первое правило Кирхгофа можно выразить словами: «Алгебраическая сумма всевозможных магнитных потоков относительно узла магнитной цепи равняется нулю.
Сформулируем второе правило для намагничивающих сил F: «В замкнутом магнитном контуре алгебраическая сумма намагничивающих сил приравнивается к сумме магнитных напряжений». Данное утверждение выражается формулой: ∑F=∑U или ∑Iω = ∑НL, где ω – количество витков, H – напряжённость магнитного поля, символ L обозначает длину средней линии магнитопровода. ( Условно принимается, что каждая точка этой линии совпадает с линиями магнитной индукции).
Второе правило, применяемое для вычисления магнитных цепей, есть не что иное, как альтернативная форма представления закона полного тока.
Примечание: Составляя уравнения с использованием формул, вытекающих из правил Кирхгофа, надо прежде определиться с положительным направлением потоков, функционирующих в ветвях, сопоставив их с направлением обходов существующих контуров.
При совпадении векторов магнитного потока с направлениями обхода (на некоторых участках), падение напряжения на этих ветвях берём со знаком « + », а встречные ему – со знаком « – ».
Методы расчетов по первому и второму законам Кирхгофа
Давайте приступим к применению на практике теоретического материала. Чтобы правильно расставить знаки в уравнениях, нужно выбрать направление обхода контура. Посмотрите на схему:
Предлагаем выбрать направление по часовой стрелке и обозначить его на рисунке:
Штрих-пунктирной линией обозначено, как идти по контуру при составлении уравнений.
Следующий шаг – составить уравнения по законам Кирхгофа. Используем сначала второй. Знаки расставляем так: перед электродвижущей силой ставится минус, если она направлена против движения часовой стрелки (выбранное нами в предыдущем шаге направление), тогда для ЭДС направленного по часовой стрелке – ставим минус. Составляем для каждого контура с учетом знаков.
Для первого смотрим направление ЭДС, оно совпадает со штрих-пунтирной линией, ставим E1 плюс E2:
Для второго:
Для третьего:
Знаки у IR (напряжения) зависят от направлением контурных токов. Здесь правило знаков такое же, как и в предыдущем случае.
IR пишется с положительным знаком, если ток протекает в сторону направления обхода контура. А со знаком «–», если ток течет против направления обхода контура.
Направление обхода контура — это условная величина. Нужна она только для расстановки знаков в уравнениях, выбирается произвольно и на правильность расчётов не влияет. В отдельных случаях неудачно выбранное направление обхода может усложнить расчёт, но это не критично.
Рассмотрим еще одну цепь:
Здесь целых четыре источника ЭДС, но порядок расчета тот же, сначала выбираем направление для составления уравнений.
Теперь нужно составить уравнения согласно первому закону Кирхгофа. Для первого узла (слева на схеме цифра 1):
I3 втекает, а I1, I4 вытекает, отсюда и знаки. Для второго:
Для третьего:
Вопрос: «Узла четыре, а уравнения всего три, почему?». Дело в том, что число уравнений первого правила Кирхгофа равно:
Nуравнений=nузлов-1
Т.е. уравнений всего на 1 меньше, чем узлов, т.к. этого достаточно, чтобы описать токи во всех ветвях, советую еще раз подняться к схеме и проверить, все ли токи записаны в уравнениях.
Теперь перейдем к построению уравнений по второму правилу. Для первого контура:
Для второго контура:
Для третьего контура:
Если подставить значения реальных напряжений и сопротивлений, тогда выяснится, что первый и второй законы справедливы и выполняются. Это простые примеры, на практике приходится решать гораздо более объёмные задачи.
Вывод. Главное при расчётах с помощью первого и второго законов Кирхгофа – соблюдения правила составления уравнений, т.е. учитывать направления протекания токов и обхода контура для правильной расстановки знаков для каждого элемента цепи.
Результат
Отлично!
Попытайтесь снова(
Выбор направления токов
Если при расчёте цепи направление токов неизвестны, то при составлении уравнений согласно законом Кирхгофа их необходимо предварительно выбрать произвольно и обозначить на схеме стрелками. В действительности направление токов в ветвях могут отличаться от произвольно выбранных. Поэтому выбранные направления токов называют положительными направлениями. Если в результате расчёта цепи какие-либо токи будут выражены отрицательными числами, то действительные направления этих токов обратны выбранным положительным направлениям.
Например
Рисунок 2
На рисунке 2,а представлен электрический узел. Произвольно, стрелками укажем направления токов (рисунок 2,б).
Важно! При выборе направления токов в ветвях, необходимо выполнения двух условий: 1. Ток должен вытекать из узла через одну или несколько других ветвей; 2. Хотя бы один ток должен входить в узел.
Предположим, что после расчёта цепи получились следующие значения токов:
I1 = -5 А; I2 = -2 A; I3 = 3 А.
Так как значение тока I1 и I2 получились отрицательными, следовательно, действительно направление I1 и I2 противоположно ранее выбранным (рисунок 3).
Рисунок 3 — действительное направление токов обозначено синими стрелками
- I1 − I2 + I3 = 0;
- -5 − (-2) +3 = 0;
- -I1 + I2 + I3 = 0;
- -5 + 2 +3 = 0.