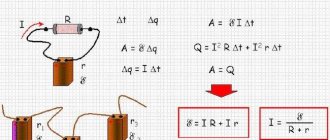
Работа по перемещению заряда в однородном электростатическом поле
Если электростатическое поле действует с некоторой силой на электрически заряженные тела, то оно способно совершить работу по перемещению этих тел.
Пусть в однородном электростатическом поле напряженностью
Вычислим работу А, которую совершает сила , действующая на заряд со стороны электростатического поля. По определению работы: A=Fscosα.
Поле однородное, поэтому сила постоянна, ее модуль равен: F=qE, а scosα=d=является проекцией вектора перемещения на направление силовых линий поля. Следовательно, работа сил однородного электростатического поля по перемещению электрического заряда q из точки 1 в точку 2 ( ) равна:
Обратите внимание! Если бы в данном случае заряд перемещался не из точки 1 в точку 2, а наоборот, то знак работы изменился бы на противоположный, то есть работа совершалась бы против сил поля.
Обратите внимание! Формула будет справедлива в случаях движения заряда по любой траектории. То есть однородное электростатическое поле является потенциальным.
Потенциальным является любое электростатическое поле: работа электростатических (кулоновских) сил (как и работа гравитационных сил) не зависит от формы траектории, по которой перемещается заряд, а определяется начальным и конечным положениями заряда. Если траектория движения заряда замкнута, работа сил поля равна нулю.
Потенциальная энергия заряженного тела в поле, созданном точечным зарядом
Заряженное тело, помещенное в электростатическое поле, как и тело, находящееся в гравитационном поле Земли, обладает потенциальной энергией. Потенциальную энергию заряда, находящегося в электрическом поле, обычно обозначают символом . Согласно теореме о потенциальной энергии изменение потенциальной энергии заряда, взятое с противоположным знаком, равно работе, которую совершает электростатическое поле по перемещению заряда из точки 1 в точку 2 поля:
Потенциальную энергию взаимодействия двух точечных зарядов Q и q, расположенных на расстоянии r друг от друга, определяют по формуле:
Обратите внимание: 1) потенциальная энергия взаимодействия зарядов положительна ( > 0), если заряды одноименные, и отрицательна ( = 0 (заряды не будут взаимодействовать). Таким образом, потенциальная энергия взаимодействия двух точечных зарядов равна работе, которую должно совершить электростатическое поле для увеличения расстояния между этими зарядами от r до бесконечности.
Распределение потенциала в электрической цепи. Потенциальная диаграмма
При расчёте электрических цепей часто возникает неопределимость в определении разности потенциалов между отдельными точками цепи и распределения потенциала цепи.
Для решения этой задачи вначале необходимо рассчитать токи в ветвях цепи.
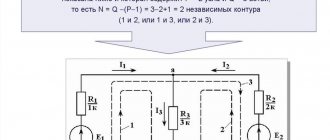
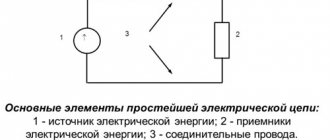
Далее потенциал одной из точек цепи (любой), например, точки на рис. 1.19, принимается равным нулю ( иногда на схеме эту точку показывают заземлённой, рис. 1.19а) и рассчитываются потенциалы всех характерных точек, выбранных для построения потенциальной диаграммы контура а,1,в,с,d,2,a.
Рис.1.19
(1.1.47)
Определив Rz= R1+ R1+ R4+ R3 и, выбрав масштабы Mφ=Mr, строится потенциальная диаграмма ( рис. 1.19б).
Таким образом, под потенциальной диаграммой понимается график распределения потенциала φ вдоль элементов замкнутого контура электрической цепи в зависимости от величины суммарного от « базовой» точки «а» до каждой последующей точки этого контура в выбранном (указанном) направлении обхода контура.
Если обход производится по ветвям, состоящим из нескольких последовательно соединённых элементов, то между каждой парой этих элементовуказывается делительная точка и её потенциал наносится на диаграмму.
Вертикальные участки диаграммы соединяют на диаграмме точками, между которыми в схеме находятся идеальные источники эдс.
Потенциал φа=φ2-Е3 должен получиться равным нулю (возрастает в исходную точку контура), т.е.последнее выражение в (1.47) является проверочным.
Потенциальная диаграмма позволяет определить напряжение между любыми точками цепи (потенциалы которых нанесены на диаграмму). Кроме того можно определить в схеме наличие точек одинакового потенциала, которые в случае необходимости можно соединить между собой без нарушения распределения токов в схеме замещения электрической цепи. Знание местоположения точек с максимальным значением потенциала позволяет установить требования на качество изоляции.
При расчёте электрических цепей часто возникает неопределимость в определении разности потенциалов между отдельными точками цепи и распределения потенциала цепи.
Для решения этой задачи вначале необходимо рассчитать токи в ветвях цепи.
Далее потенциал одной из точек цепи (любой), например, точки на рис. 1.19, принимается равным нулю ( иногда на схеме эту точку показывают заземлённой, рис. 1.19а) и рассчитываются потенциалы всех характерных точек, выбранных для построения потенциальной диаграммы контура а,1,в,с,d,2,a.
Рис.1.19
(1.1.47)
Определив Rz= R1+ R1+ R4+ R3 и, выбрав масштабы Mφ=Mr, строится потенциальная диаграмма ( рис. 1.19б).
Таким образом, под потенциальной диаграммой понимается график распределения потенциала φ вдоль элементов замкнутого контура электрической цепи в зависимости от величины суммарного от « базовой» точки «а» до каждой последующей точки этого контура в выбранном (указанном) направлении обхода контура.
Если обход производится по ветвям, состоящим из нескольких последовательно соединённых элементов, то между каждой парой этих элементовуказывается делительная точка и её потенциал наносится на диаграмму.
Вертикальные участки диаграммы соединяют на диаграмме точками, между которыми в схеме находятся идеальные источники эдс.
Потенциал φа=φ2-Е3 должен получиться равным нулю (возрастает в исходную точку контура), т.е.последнее выражение в (1.47) является проверочным.
Потенциальная диаграмма позволяет определить напряжение между любыми точками цепи (потенциалы которых нанесены на диаграмму). Кроме того можно определить в схеме наличие точек одинакового потенциала, которые в случае необходимости можно соединить между собой без нарушения распределения токов в схеме замещения электрической цепи. Знание местоположения точек с максимальным значением потенциала позволяет установить требования на качество изоляции.
Свойства потенциала
Среди важных свойств потенциала надо отметить следующие:
- если поле создается несколькими зарядами, то потенциал в конкретной точке будет равен алгебраической (с учетом знака заряда) сумме потенциалов, создаваемых каждым из зарядов φ=φ1+φ2+φ3+φ4+φ5+…+φn;
- если расстояния от зарядов таковы, что сами заряды можно считать точечными, то суммарный потенциал считается по формуле φ=k*(q1/r1+q2/r2+q3/r3+…+qn/rn), где r – расстояние от соответствующего заряда то рассматриваемой точки.
Если поле образовано электрическим диполем (двумя связанными зарядами противоположного знака), то потенциал в любой точке, находящейся на расстоянии r от диполя будет равен φ=k*p*cosά/r2, где:
- p – электрическое плечо диполя, равное q*l, где l – расстояние между зарядами;
- r – расстояние до диполя;
- ά – угол между плечом диполя и радиус-вектором r.
Если точка лежит на оси диполя, то cosά=1 и φ=k*p/r2.